多工厂环境下考虑个体利益的多目标协同生产计划模型及算法

景 熠， 李 琴

(重庆理工大学 管理学院，重庆 400054)

0 引言

网络化多工厂协同制造模式下，大型制造企业利用先进信息技术和物流技术，将分布在不同地域的多个工厂的资源进行综合管理并协同调度，从而优化资源配置、降低企业运作成本，最终提高企业的经济效益。例如，上海通用汽车有限公司利用计算机网络信息技术，将分布在上海、烟台、沈阳和武汉等地区的多个生产基地进行连结，以实现多个工厂的协同运作，可以合理的安排资源和调度产能。由此可见，多工厂协同制造模式已逐渐成为大型制造企业经营管理的主要发展方向，如何在日常运营中优化多工厂协同生产计划，也成为企业界和学术界关心的热点问题。

对于多工厂协同生产计划问题，近年来国内外学者进行了较深入的研究，取得了一些成果。Behnamian[1]以最小化运作成本为优化目标，对分布式多工厂协同生产计划问题建立了数学模型，并设计了对应的类电磁机制求解算法。Karimi和Davoudpour[2]针对多工厂供应链生产和批量交付计划问题，采用分枝定界法进行求解。在此问题基础上，Karimi和Davoudpour[3]进一步考虑各阶段的库存持有成本，提出了时间索引公式进行求解，以权衡持有成本和交付成本。Liu等[4]以最小化运营成本为优化目标，构建了基于动态蜂窝制造系统的多工厂设施转移和生产计划模型，并引入五阶段启发式规则，设计了相应的综合细菌觅食算法进行求解。Hafezalkotob等[5]考虑各工厂之间共享库存和劳动力，以最小化总成本为优化目标，构建了多工厂协同生产计划模型，并应用四类合作博弈理论量化了各工厂之间的成本节约和协同效应。Ruiz-Torres等[6]将最小化生产-运输总成本和最小化延迟交付率同时作为两个优化目标，构建了具有时间和地点限制的协同计划模型，并设计了四类启发式算法进行求解。Entezaminia等[7]考虑生产成本与绿色标准之间的权衡，以最小化总损失和最大化环境分值为优化目标，构建了绿色供应链生产计划模型，并采用LP指标方法进行求解。Makui等[8]针对使用期限非常有限的产品的综合生产计划问题，以最小化总成本为优化目标，构建了不确定条件下的多工厂生产计划模型，并设计了改进的Benders分解算法进行求解。Gholamian等[9]针对不确定条件下的多目标、多产品、多工厂协同生产计划问题，以最小化总成本和缺货率为优化目标，构建了多目标混合整数非线性规划模型，并采用模糊多目标优化技术进行求解。刘洪伟等[10]对集团分布式制造模式下的生产调配问题进行了研究，并设计了基于两段式编码规则的求解算法。曹立思等[11]针对多个平行机工厂和多个客户的供应链排序问题，构建了制造商订单分配、车间生产调度和运输计划模型，并基于线性规划松弛技术和遗传算法设计了两段式求解过程。来玉新等[12]考虑各个工厂之间存在供需关系，以最小化总生产成本为优化目标，构建了成本参数、客户需求和机器能力均不确定环境下的网络型多工厂协作生产计划模型，并运用区间优化方法进行求解。

在此基础上，一些学者将再制造活动整合到多工厂生产系统中，研究了多工厂协同环境下的制造/再制造生产计划问题。赵忠和谢家平[13]针对具有回收中心和分销中心的分布式多工厂闭环供应链系统，以最小化运作总成本为优化目标，构建了协同生产计划模型，并运用分枝定界法进行求解。景熠等[14]在市场需求和回收产品供应数量不确定环境下，针对闭环供应链系统，构建了三层协同生产计划模型，并设计了基于双倍体自适应遗传算法的分层迭代策略进行求解。

通过对上述文献的梳理可以看出，现有多工厂协同运作研究中，都是以系统整体绩效最大化为优化目标(包括总收益最大化、总成本最小化、总延迟最小化等)，而没有考虑各个工厂在协同系统中的个体利益诉求。在任何经济活动中，个体利益和整体利益不可能完全一致[15]，但只有在个体利益得到基本满足的前提下，才有可能达到整体利益最大化的状态[16]。对于多工厂协同运作系统，单纯追求整体收益的最大化，忽视各个工厂的个体利益，不仅会激化工厂之间的竞争矛盾，还会导致制定出的协同计划得不到全面、有效的执行，难以真正形成网络集成的协同效应。

因此，本文研究的多工厂协同生产计划问题，与以往的研究相比，具有以下特点：①将最大化系统整体收益作为第一个优化目标，从网络集成的角度协调分布式多工厂的生产、库存和运输活动；②考虑各个工厂的个体利益诉求，基于亚当斯的公平理论，利用偏离系数法设计个体收益平衡偏差，并将其作为第二个优化目标，进而实现整体利益和个体利益的一致性导向；③结合模型结构特点，设计了多目标遗传算法进行优化求解。

1 问题描述

本文针对由多个工厂和多个需求中心组成的分布式系统，研究多周期、多产品的协同生产计划问题。在该系统中，制造企业(集团)为了扩大产业版图、优化资源配置，在不同区域布局了多个工厂，各个工厂可生产该企业部分或全部类型的产品，并根据下游不同市场区域的订单需求，将这些产品运往各个需求中心。每个需求中心可以选择一个或多个工厂为其供应产品。

进一步，根据建模的实际情况，作如下说明：①各个工厂存在个体利益诉求，如果个体利益得不到基本满足，即实际利润与应得利润差距过大，可能导致部分工厂不合作、不协同，进而影响整个协同生产计划的有效执行；②不同工厂的个体利益诉求会存在一定差异，即各个工厂会基于自身投资规模、生产能力、设备水平等因素(投入水平)，判断个体应得利润(产出水平)的高低；③为了平衡工厂之间的订单分配，产品销售采用“包邮”方式，即运输成本由工厂承担；④所有需求中心的订购量必须全部满足。

2 模型基本变量和参数

模型所涉及的主要变量和参数如表1～3所示。

表1 下标符号及其含义

表2 变量符号及其含义

表3 参数符号及其含义

3 多工厂协同生产计划模型

3.1 目标函数1：最大化整体收益

依据上述问题描述和符号定义，首先以Fi表示各个工厂的实际利润，其中收入部分为全部产品的销售额，成本部分由产品生产成本、库存成本和运输成本组成，即Fi可以表示为：

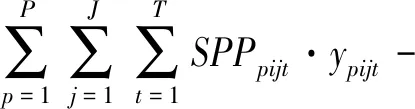
(1)

然后，将最大化计划周期T内I个工厂的系统总利润F作为第一个优化目标，即可表示为

(2)

3.2 目标函数2：最小化个体收益平衡偏差

在正常生产条件下，工厂固定投入越多，生产规模越大。因此，本文以生产规模表征各个工厂的投入水平，计算各个工厂的理论利润分配率gi，可表示为

(3)

依据亚当斯的公平理论，各个工厂的应得利润即为gi·F。在此基础上，利用偏离系数法，设计个体收益平衡偏差，并以其最小化作为第二个优化目标，即可表示为

(4)

偏离系数法可以衡量2个变量之间的平均偏离程度。当个体收益平衡偏差ED越小，则表示实际利润Fi和应得利润gi·F之间的偏差越小，各个工厂的利益分配越趋于平衡。

3.3 约束条件

除了式(2)和式(4)两个优化目标，多工厂协同生产计划模型还应当满足下列约束条件：

1)产品的库存平衡公式，可表示为

(5)

2)各个工厂的最小发运量约束，可表示为

(6)

3)需求中心的产品交付约束，可表示为

(7)

4)产品的库存容量限制，可表示为

(8)

5)产品的生产能力限制，可表示为

xpit·pbp≤MPpi·λpit,∀p,i,t

(9)

6)非负整数约束，可表示为

xpit,ypijt,αpit∈N,∀p,i,j,t

(10)

4 基于多目标遗传算法的模型求解过程

4.1 总体流程

步骤1初始化种群。确定算法的初始编码规则，并设置种群最大进化代数M和种群规模N。

步骤2选择操作。对当前种群进行快速非支配排序，并计算种群中每个个体的目标函数值、约束违反量和拥挤度值；在此基础上，以二元锦标赛方法进行选择操作。

步骤3交叉和变异操作。采用王小平和曹立明设计的自适应公式[17]，根据算法进化态势实时调整交叉概率和变异概率，并分别对依概率选中的个体进行双点交叉操作和逆序变异操作。

步骤4种群合并。将初始种群(父代种群)和经过交叉、变异之后形成的种群(子代种群)进行合并，组成一个规模为2×N的融合种群。

步骤5对规模为2×N的融合种群进行快速非支配排序。计算融合种群中每个个体的目标函数值(总利润和个体利益平衡偏差)，并依据快速非支配规则进行排序。

步骤6填充规模为N的新种群。首先将融合种群中非支配等级序值为1的个体加入到新种群中；如果数量小于N，则继续加入等级序值为2的个体，以此类推；如果加入某等级个体后，个体数量超过规模上限，则将该等级中拥挤度值较小的个体淘汰。

步骤7循环运行。判断进化代数m是否达到设置的最大值M，如果达到则进入步骤8，否则循环进入步骤2。

步骤8输出最佳均衡解。算法结束后，从Pareto最优解集中，选择一个“最优”个体，作为最终输出的计划方案。

在上述步骤中，步骤3、步骤4、步骤6、步骤7较为简单，不再阐述；而对于步骤1、步骤2、步骤5、步骤8中涉及的编码规则、快速非支配排序规则、拥挤度值计算方法、多目标二元锦标赛选择操作、最佳均衡解输出规则，将分别进行详细设计。

4.2 编码规则

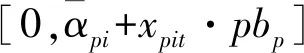
4.3 快速非支配排序规则

首先，在当前种群中，筛选出所有的非支配个体，将其设定为第一等级；然后将第一等级的个体全部移出，再在剩余的个体中筛选出新的非支配个体，将其设定为第二等级；以此类推，直至种群中的所有个体都被排序。

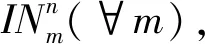
4.4 拥挤度值计算

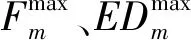
4.5 多目标二元锦标赛选择操作

通过计算个体的适应度值来判断个体优劣，从而确定保留个体，这是大多数遗传算法在选择操作设计中常用的方法，但这种方法会引入新的外生参数，降低算法的性能。因此，本文将Zaman等[18]针对单目标优化问题设计的无参数选择操作，进一步拓展到多目标优化问题中。该选择操作每次随机、有放回的从父代种群中抽取、比较两个个体，其中较好的个体将被保留到子代种群中；重复抽取、比较次之后，结束该轮选择操作。同时，两个个体的二元锦标赛比较规则如下：

①如果两个个体均为可行解，则将等级序值较小的个体保留到子代种群中。

②如果两个个体均为可行解，且等级序值相同，则将拥挤度值较大的个体保留到子代种群中。

③如果其中一个个体为可行解，而另一个个体为非可行解，则将可行个体保留到子代种群中。

④如果两个个体均为非可行解，则将约束违反量较小的个体保留到子代种群中。

4.6 最佳均衡解输出规则

NSGA-II的求解结果是Pareto最优解集，而在生产实践中，需要得到一个确定的计划方案。因此，为了进一步获得唯一的“最优”个体，采用下列公式计算每个Pareto最优个体的均衡度函数值

其中，LFmax、LFmin分别为Pareto最优解集中总利润最大值和最小值；LEDmax、LEDmin分别为Pareto最优解集中个体利益平衡偏差的最大值和最小值；选取均衡度函数值最小的个体，作为最佳均衡解。

5 仿真试验

5.1 算例描述

本节从某一汽车发动机生产企业获取基础数据样本。该生产企业由分布在不同区域的三个发动机生产工厂(I=3)组成，可生产包含Ⅰ型、Ⅱ型、Ⅲ型三种四缸电喷式发动机(P=3)，以向下游不同市场区域的五个需求中心(J=5)提供产品和服务。其中，第一个工厂仅生产Ⅱ型和Ⅲ型发动机，第二个工厂和第三个工厂能够同时生产三种型号的发动机。

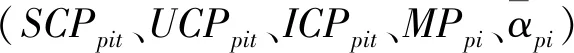
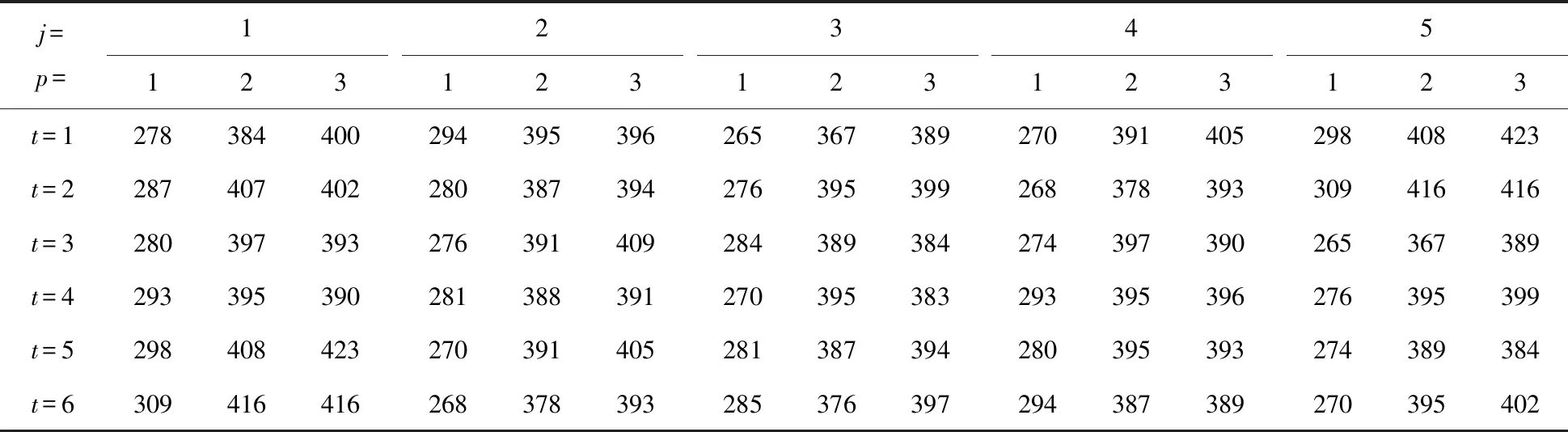
表4 各个需求中心的需求量

表5 各个工厂的内部运作参数

表6 各个工厂到需求中心的运输成本

表7 各类产品的销售价格

5.2 求解结果及其对比分析

利用仿真软件Matlab2017a编译考虑个体利益的多目标计划模型及其求解算法，得到产品生产批数xpit的求解结果如图1～3所示。同时，将多目标计划模型求解得到的收益结果与单目标(仅考虑整体收益最大化)模型进行对比，如表8所示。

图1 xpit(i=1)的求解结果(单位:批)

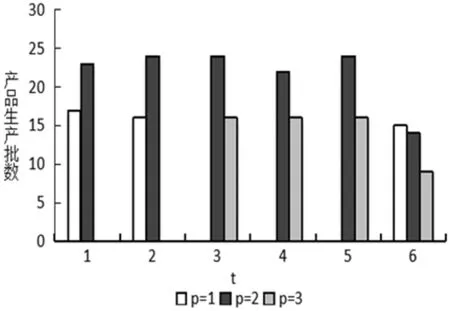
图2 xpit(i=2)的求解结果(单位:批)

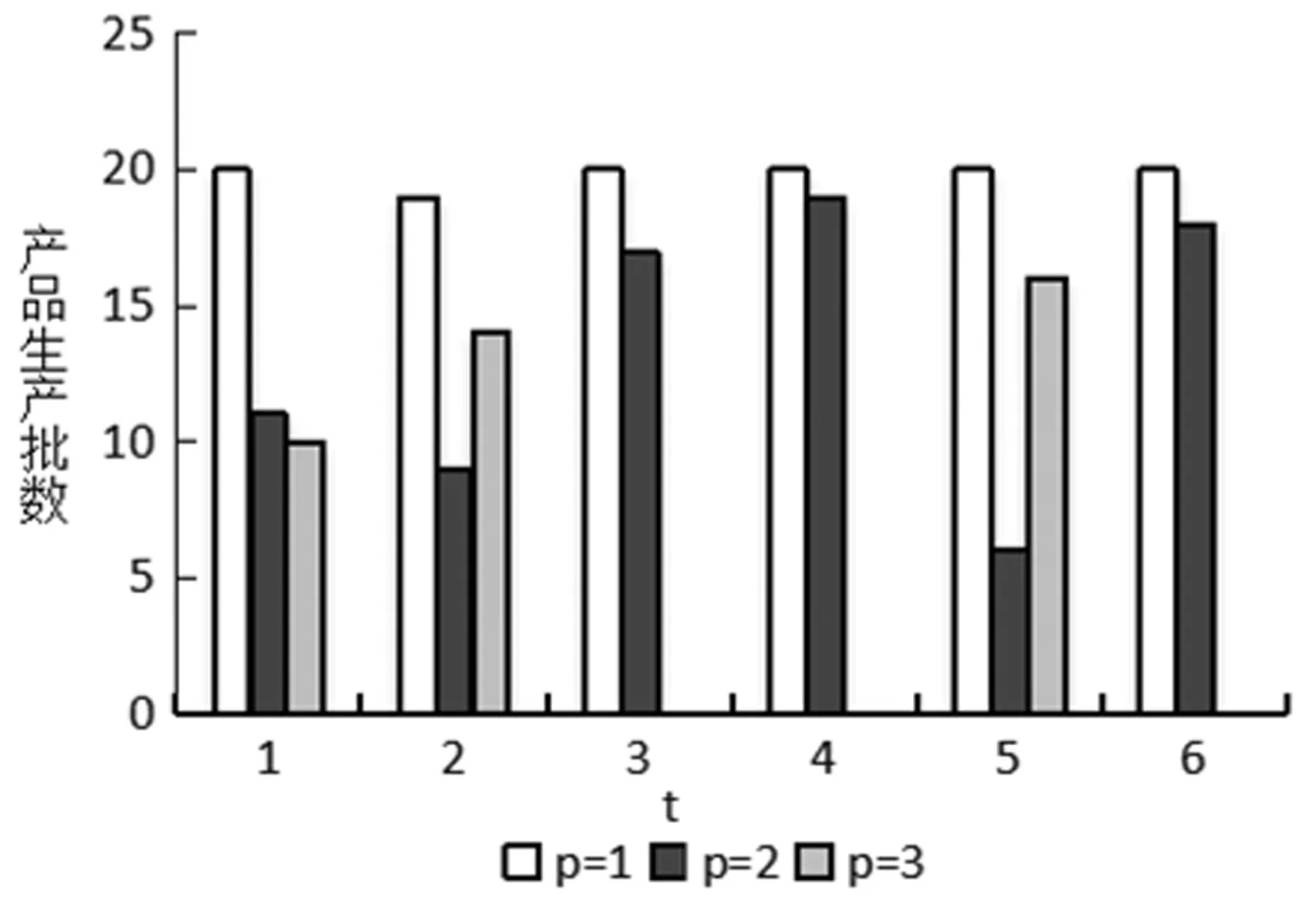
图3 xpit(i=3)的求解结果(单位:批)

表8 多目标计划模型与单目标计划模型的收益结果对比

从上述对比结果可以看出，单目标计划模型可以最大限度的提升多工厂协同生产系统的整体收益；但是，工厂3的实际利润仅为1397262，不足其应得利润的50%。为了追求整体收益的最大化，牺牲了部分工厂的利益，可能造成这些工厂的不合作、不协同，即便制定出了协同生产计划，也难以得到有效执行。

而多目标计划模型在追求整体收益最大化的同时，兼顾了个体利益诉求和利益平衡，尽可能缩小了各个工厂实际利润与应得利润的偏离差异程度，杜绝了部分工厂利益严重受损的情况，从而确保了个体参与的积极性；同时，相较于单目标计划模型，系统整体收益仅下降了0.86%。最终，各个工厂的个体利益和系统整体收益均得到了有效保障。

6 结束语

本文针对由多个工厂组成的分布式系统，以最大化整体收益和最小化个体利益平衡偏差为优化目标，构建了协同生产计划模型，并依据多目标模型结构特点，基于NSGA-II，设计了相应的求解过程。在本文中，“协同”思想实际体现在两个层面：一是从网络集成角度协调了各个工厂的生产、库存和运输活动，合力满足了下游不同区域的市场需求；二是协调了各个工厂个体利益之间的平衡，实现了整体利益和个体利益非一致性的最小化。

同时，针对多工厂分布式系统中个体利益的平衡问题，仍有进一步探讨的空间。例如，可以考虑战略性扶持因素和个体利益对整体利益的妥协程度对协同系统的影响，也可以考虑产业链上下游不同工厂之间的利益平衡。