乏燃料剪切机气固两相流分析及结构优化

黄 辉，王时龙,*，马 驰，周 杰，董建鹏，周科源

(1.重庆大学 机械传动国家重点实验室，重庆 400044；2.中国原子能科学研究院 放射化学研究所，北京 102413)

乏燃料是在核反应堆中使用完毕后卸出的核燃料，国际上有一次通过长期地质贮存和闭式循环回收再利用两种处理策略，我国确定实行后者，回收乏燃料中大量有用的核资源、分离长寿命放射性核素，结合嬗变技术，减少最终地质处置量，提高核能整体经济性，从而保证核能的可持续发展，同时减少环境辐射污染。闭式循环回收再利用的一个重要环节就是采用以锕系元素萃取分离为主工艺的核燃料后处理，该流程就是对核燃料进行破解和溶解，进而进行萃取分离。燃料组件的破解是第一步，技术路线较多，目前普遍采用机械法剪切设备将核燃料处理成符合溶解需求的碎料。剪切机作为该设备的核心机械，设计时需考虑多方面的需求，如剪切时会产生大量强放射性核燃料芯块粉尘，设计时需确保放射性粉尘尽可能保留在剪切机设备腔体内，防止扩散出污染热室，导致无法进入热室对其中的设备进行维修，必须将这些粉尘通过密封、气流走向控制等设计首端进行严密隔离，并确保大部分乏燃料芯块从剪切机流道内排入化学溶解器，保证放射性包容的同时，提高后处理的回收率。通过研究剪切机内污染性粉尘颗粒的分布和运动规律来降低剪切机内粉尘沉积水平是新型剪切机设计的重点。

传统剪切机的设计并未涉及粉尘颗粒对乏燃料剪切机设计的影响以及气固流边界条件对粉尘颗粒运动分布的影响[1-4]，因而通过传统的剪切机设计方法[5-7]不能设计出满足降尘溶尘要求的剪切机。剪切机内粉尘颗粒分布运动问题属于流体动力学范畴，但一些研究流体动力学的方法，尚未在剪切机的设计上得到应用，且这些流体动力学方法在应用时，往往需要根据具体对象的特性和待研究的物理量等的不同来进行选择[8-11]，一般不能直接相互借鉴经验。本文拟对乏燃料剪切机内气固流的分布运动规律进行数值模拟研究，包括数值模拟方法的选取、流道结构和边界条件对气固流分布运动的影响，进一步对剪切机的结构和边界条件进行优化，最终达到降低剪切机内粉尘沉积水平的目的。

1 模型建立和网格划分

1.1 乏燃料剪切机实体模型建立

本文乏燃料剪切机的设计相比于传统剪切机的设计，增加了通排气和降尘溶尘的设计要求，其所剪切的乏燃料是由上、下两段组成的材料。根据剪切机的功能要求以及设计理论，建立了剪切机几何实体模型，如图1所示。气流运动的路径大致为：外部通入的气流分别从1个乏燃料进气口、2个空气喷嘴进气口、1个箱体后区侧壁进气口进入到剪切机内，然后经过剪切处的气流通道进入分料器溜槽，最后从溜槽排出后进入溶解器[12]。溶解器主体呈扁平圆柱形，其内部有溶解轮和溶解液，剪切机溜槽与溶解器的中心相连接，剪碎的乏燃料进入溶解器后，溶解轮围绕溶解器中心步进式旋转，使得碎料分散到溶解液中。由此剪切机内的污染性粉尘颗粒在气体的携带作用下进入溶解器中被溶解吸收，达到降尘溶尘的目的。

1.2 剪切机内流场实体模型建立

由于剪切工位在剪切乏燃料时的模型最复杂，故本文选取的建模对象是剪切机剪切乏燃料时形成的相对结构，对其建立流体域模型，且考虑到本文研究的重点是剪切机内的流体域，在确保关注部位分析精度的前提下，对剪切机进行如下假设和简化：1) 忽略几何模型中小的圆角及倒角；2) 相对固定的结构视为一个整体；3) 忽略剪切机箱体外部的机构附件；4) 忽略剪切机内部机构的内部附件；5) 剪切机内产生的粉尘颗粒用Al2O3球形颗粒代替。简化后的几何模型如图2所示。在ANSYS DM中对简化几何模型的内流场进行抽离，得到剪切机内流场实体模型，如图3所示。

图1 剪切机几何实体模型Fig.1 Solid model of shearing machine

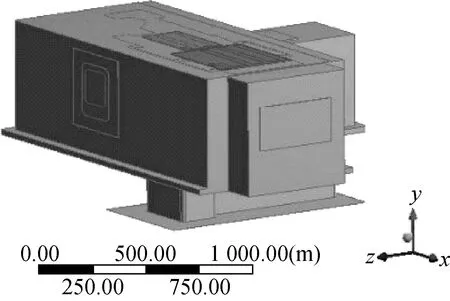
图2 剪切机简化几何模型Fig.2 Simplified solid model of shearing machine

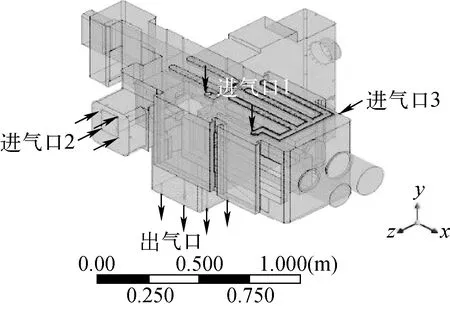
图3 剪切机内流场模型Fig.3 Flow field model of shearing machine

1.3 内流场实体模型网格划分

采用ICEM CFD软件对流体域模型进行网格划分，选用非结构化网格。同时采用Patch Conforming Method对较重要区域的网格进行细化和加密，以提高数值计算的精度。剪切机内流场的网格划分如图4所示。

图4 剪切机内流场的网格划分Fig.4 Meshing of flow field

1.4 内流场数值模型建立

1) 气相数值模型建立

(1) 流动状态确定。本文研究对象的环境温度为25 ℃、大气压力为101 kPa。考虑到剪切阱附近的结构尺寸较大且大部分气流处在剪切阱附近，选取过剪切阱大截面处的气流来评估剪切机内气流的流动状态。本文的气流管道为矩形截面，选取雷诺数(Re)的计算公式为：

Re=4vR/μ

(1)

R=ab/2(a+b)

(2)

其中：v为气流平均速度；R为矩形通流截面的水力半径；a和b分别为矩形流通截面的长度和宽度；μ为气流的动力黏度。

根据剪切机实际工作要求，在截面处测得v=3.2 m/s；矩形截面的长度为1.25 m、宽度为0.7 m，R=0.224 4；查表得气体的动力黏度μ=1.844 8×10-5Pa·s。计算得Re=155 698，大于2 300，可知剪切机内的气流处于湍流状态，所以采用湍流模型进行模拟计算。

(2) 湍流模型选取。从计算能力和精度看，Standardk-ε以及RNGk-ε模型是目前常用的2种模型。Standardk-ε模型中，湍动能方程k是精确推导计算，而湍流耗散率输送方程ε建立在经验公式上。RNGk-ε模型建立在严格的统计技术上，与Standardk-ε模型相比，其处理高、低雷诺数的复杂湍流的能力更强[11]，本文选用RNGk-ε模型。

(3) 数值模拟方法选取。湍流数值计算有3种常用的数值方法：直接数值模拟法、大涡模拟法和雷诺平均法。雷诺平均法解决了直接数值模拟法计算量大的问题，避免了瞬时N-S方程的复杂非线性造成的精确描述三维流场以及时间特性相关全部细节的困难，其通过时均化的N-S方程将瞬态脉动量表现出来，对于解决工程实际问题，湍流的整体效果(即平均流场的变化)才是最重要的，而了解每个瞬态流场的全部细节对于解决工程实际问题帮助不大[13]。因此，本文采用雷诺平均法建立气相数值模型。

(4) 气相控制方程。由于剪切机内气体流速远低于声速，气相的动力黏度μf以及密度ρf可认为不变，忽略热交换和体积力影响，得到气相控制方程。

连续性方程为：

(3)

动量方程为：

(4)

其中：τ为气相应力张量；β为相间动量交换系数；ε为耗散率；t为时间；uf为颗粒所在位置的流场速度；up为颗粒的运动速度。

2) 颗粒相数值模型建立

(1) 两相流中颗粒的运动及受力分析。由牛顿第二定律可知，两相流中任一颗粒的受力满足mpdup/dt=∑F，mp为颗粒质量，∑F为颗粒所受外力的合力，包括颗粒受到的重力、浮力、斯托克斯阻力、压力梯度力、附加质量力、贝塞特力、马格努斯力、萨夫门力、曳力、泳力等。通过分析和计算，有些力数值很小，对数值模拟几乎无影响，可忽略不计，本文主要考虑颗粒受到的重力和斯托克斯阻力的作用。

(2) 颗粒与壁面的相互作用。颗粒与壁面碰撞时，相互作用形式主要有反弹、粘附和逃逸。不同作用形式分别对应不同的壁面函数。在本文研究中，可近似认为颗粒与壁面之间的碰撞结果为反弹，且假设壁面无滑移，故考虑采用Scalable壁面函数[14]。

(3) 颗粒相基本运动方程。本文以湍流模型为基础，采用在拉格朗日坐标系下进行颗粒运动追踪的随机轨道模型，用瞬时运动方程和随机方法模拟湍流。由于模拟的粒径和雷诺数相对较小，所以用经典模型来描述。为追踪粒子，引入以下假设：追踪颗粒是具有相同直径和密度的球体；颗粒密度远大于流体的密度，忽略浮力、压力梯度力及其他较小的力；虽然剪切瞬间剪切位置粉尘颗粒产生量较密集，但考虑到颗粒会快速扩散及本文研究对象是剪切机的整个气固两相流而非剪切位置处的局部流体，此时颗粒相的体积浓度很小，可视为稀相，忽略粒子间的相互碰撞作用；忽略流体中的颗粒体积(非常小)，颗粒的存在不影响气体压力；忽略温度变化对流场的耦合影响及空气含水量对空气参数的影响。

基于上述假设，只考虑颗粒的重力和斯托克斯阻力。根据牛顿第二定律，单个粒子的运动方程可表示为：

|uf-up|(uf-up)/8+mpg(ρp-ρf)

(5)

在式(5)中代入颗粒阻力系数CD及颗粒相对雷诺数Rep的公式，颗粒的运动方程可改写为：

dup/dt=3μCDRep(uf-up)/

(6)

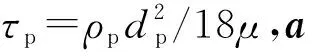
up=uf+aτp/f+(up-uf-aτp/f)·

exp(-fΔt/τp)

(7)

xp=xf+(μf+aτp/f)Δt+

τp(μp-μf-aτp/f)(1-exp(-fΔt/τp))

(8)

(4) 气固两相耦合模型的选取。对于颗粒相为稀相的气固两相流，颗粒相和流体相之间的相互作用可分为单向耦合和双向耦合两种。本文颗粒体积浓度较低，一般情况下采用单向耦合即可满足研究要求[15]。

2 数值求解方法和边界条件

2.1 对流方程的离散

CFX在计算流体域模型前，要先对计算区域进行离散化处理。目前，有3种应用最广泛的离散方法：有限元法、有限体积法和有限差分法[16]，其中有限体积法综合了其他2种方法的优点[17]，求解方便，且求解精度满足本文研究对象的要求。因此，选用有限体积法进行模拟计算。

CFX在进行非稳态求解时，有两种精度选择：一阶向后欧拉以及二阶向后欧拉。一阶格式一般用于流体流动方向与网格成一条线的情况，此时求解的数值耗散相对较低；当流体流动方向与网格不在一条线时，对于各种多边形网格，一般均采用二阶格式，以此降低离散的误差，提高求解精度，特别是当流体流动很复杂时，二阶格式能较一阶格式获得更好的计算结果[18]。所以，本文采用二阶离散格式来对流场模型求解。

2.2 流场迭代求解方法

本文采用的CFX可对各种流动进行质量守恒和动量守恒的求解。气固两相流耦合的问题主要是气相和固相之间速度和压力的耦合，由此需要解决以下2个问题：1) 在使用常规网格以及中心差分方法进行离散时，离散后的动量方程不能判断压力场是否合理；2) 在动量守恒方程中，压力一阶导是以源项表示的。针对第1个问题，可通过采用交错网格来解决，而对于第2个问题，现阶段最可靠的解决方案是SIMPLE算法。该算法的核心是“猜测-修正”原则，通过不断的迭代，最终得到满足要求的收敛解。该算法可求解交错网格上的压力场，进而对动量方程求解，是目前计算不可压流场问题的主要方法。所以本文采用SIMPLE算法来计算。

2.3 边界和输入条件

根据剪切机实际工作要求，测量并通过收敛得到剪切机的进出口边界条件：进气口1气流流速为1.000 m/s，进气口2为1.000 m/s；进气口3为3.740 m/s；出气口的相对压力为-1 100 Pa。输入条件包括流场中气体和颗粒的物性参数。流场中气体的物性参数如下：材料为空气；温度为25 ℃；密度为1.169 kg/m3；动力黏度为18.448 μPa·s。根据剪切机实际工作情况，剪切阱附近是产生粉尘颗粒的主要位置，故在气固两相流模型中选取乏燃料剪切阱附近的3个位置(1、2、3)进行颗粒注入。颗粒的物性参数如下：材料为Al2O3、球状、密度为3 700 kg/m3、直径为50 μm、初始速度为1.000 m/s、数量为300×3。

3 数值计算结果及分析

3.1 气相模拟计算结果

本文模型为流固耦合，采用二阶差分和SIMPLE算法，求解量较大，综合CFX与Fluent的优劣对比，采用CFX更适合本文的计算。本文使用CFX 19.0进行计算。

考虑到剪切机内流场的形态复杂，无法采用规则的平面或区域来描述流场中气流的形态，本文选取3个平面(经过剪切阱，剪切阱区域如图5所示)来描述流场中气流的流动，3个平面分别为：平面1(z=3.245 m)、平面2(y=0.08 m)、平面3(x=-0.452 66 m)。

模拟得到的剪切机内平面1、2、3上气流速度和湍动能的分布如图6、7所示。在平面1上，速度最大的区域在剪切刀附近，为12.78 m/s，湍动能也主要分布在剪切刀附近，分布范围为0.224 8～0.899 0 m2/s2。在平面2上，速度最大的区域为剪切箱体后区靠近偏心滚筒的位置，分布范围为4.126～16.500 m/s，湍动能也主要分布在该区域(0.374 0～1.494 0 m2/s2)。在平面3上，速度最大的地方出现在剪切阱附近，为19.04 m/s，且可见大面积的涡流出现，湍动能为0.426 3～1.705 0 m2/s2，主要分布在进料口中程处以及溜槽处。

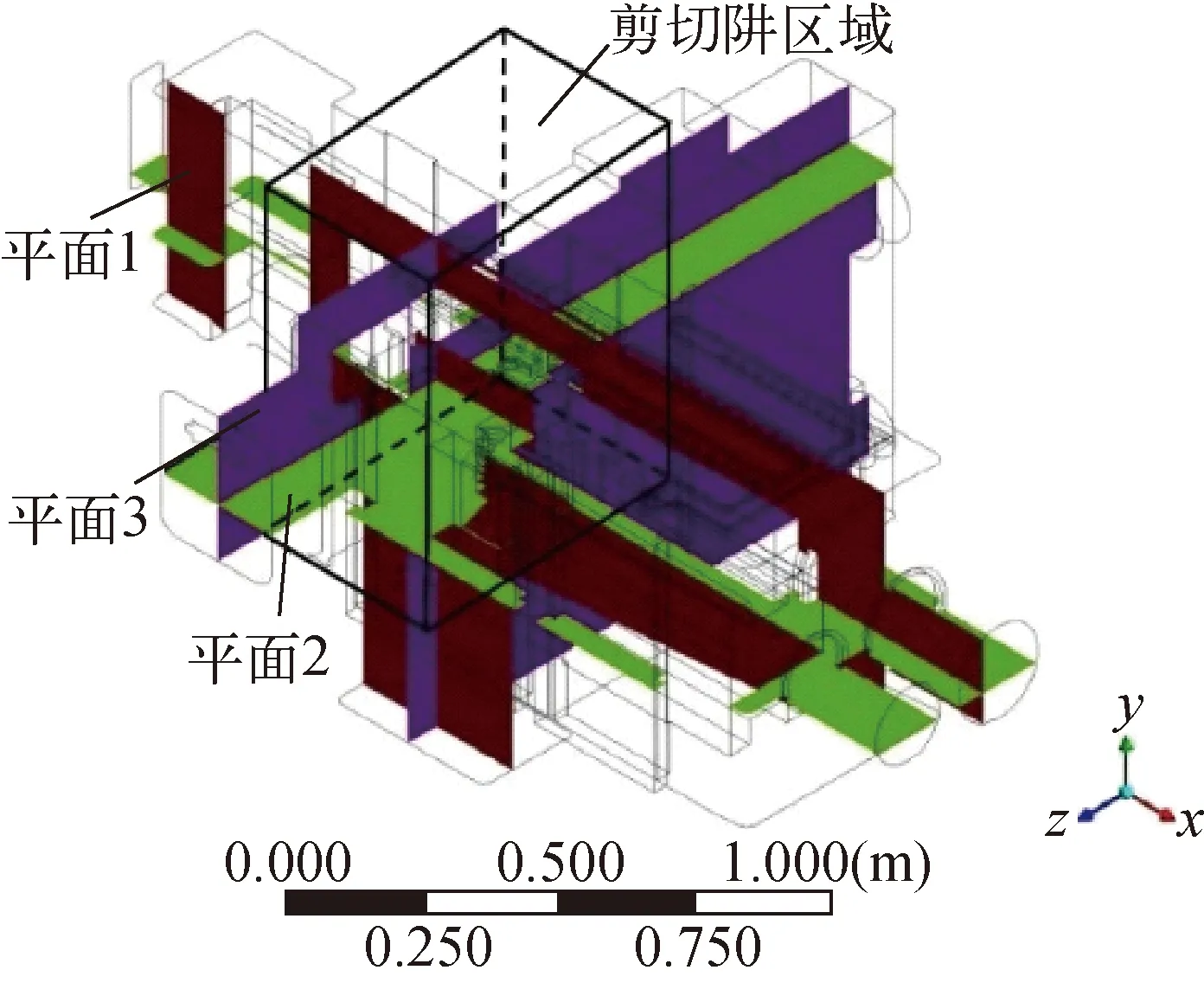
图5 剪切阱及3个参考平面Fig.5 Shear well and three reference planes

剪切机内气流压力、速度分布流线图如图8所示。从图8可看出，剪切机内气流最大压力出现在剪切口上方，最大速度出现在刀具附近。流线图显示气流在剪切室后区形成大面积的涡流，阻碍了气流的运动，使得粉尘颗粒随气流一直在剪切箱体内打转而无法顺利排出剪切箱体。分析可知，气流旋涡的形成主要是由进气口3的气流运动造成的。综上所述，对剪切阱附近的结构以及剪切箱体后区进气口位置进行优化非常迫切。

图6 平面1、2、3上气相速度矢量图Fig.6 Vector diagram of gas velocity on plane 1, 2 and 3

图7 平面1、2、3上的湍动能分布Fig.7 Turbulent kinetic energy distribution on plane 1, 2 and 3

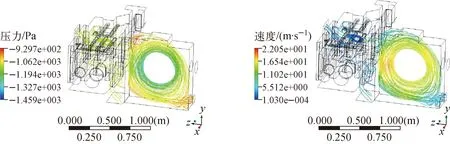
图8 剪切机内气流压力和气流速度流线图Fig.8 Pressure streamline and velocity streamline of gas

3.2 结构改进及模拟

由前述模拟结果和分析可知，箱体结构可优化位置有两处：剪切阱附近的结构、箱体后区侧壁进气口位置。由于本项目缺乏剪切阱附近结构的设计要求，无法对其作出改动，故本文选择对箱体后区侧壁进气口位置进行优化。优化方案为：将剪切机箱体后区侧壁进气口去掉，改为从箱体下方的乏燃料上段溜槽口进气。为实现上段溜槽口进气均匀，可在上段溜槽口下方接一漏斗形进气嘴。改进后得到的内流场模型及进出气口分布如图9所示。

改进进气口3位置后，进行数值模拟，得到平面1、2、3上气流的速度和湍动能分布，如图10、11所示。分析图10、11可知：改进进气口3位置后，在平面1上，气流速度最大处出现在溜槽的中部，约为23.45 m/s，湍动能主要分布在溜槽两侧壁面处，约为0.177 1～0.711 6 m2/s2，气流速度最大的位置及湍动能的分布和大小较之前有所改善，可降低对剪切阱附近结构的破坏；在平面2上，剪切阱处的气流流速较大，约为3.576～14.300 m/s，湍动能主要分布在剪切阱附近，约为0.184 4～0.737 5 m2/s2；在平面3上，乏燃料剪切处周围的气体流速较大，约为3.960～15.84 m/s，湍动能主要分布在溜槽前后壁面，约为0.275～1.100 m2/s2，与改进前的剪切处相比，可在一定程度上起到降低刀具损耗速度的作用。比较改进前后3个平面上的气流速度分布以及湍动能分布可知，进气口3位置改进后，同一平面上的速度和湍动能均有所下降，且其空间分布更有利于降低剪切刀的损耗，并在一定程度上延长剪切机的工作寿命。

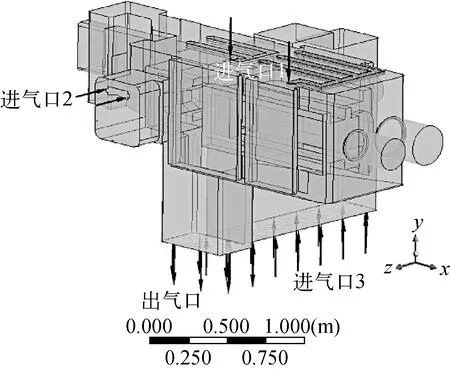
图9 改进后的内流场模型Fig.9 Improved flow field model

进气口3位置改变后，通过CFX模拟，剪切机内气流的压力、速度分布的流线图如图12所示。分析图12可知，改进进气口位置后，气流的形态有了很大改善，没有了改进前的大面积旋涡，气流路径较为通畅，气体从各进气口进入后经过剪切室内部顺利从出气口排出，能有效携带剪切箱体内的粉尘颗粒进入溶解器。

图10 改进后平面1、2、3上的气相速度矢量图Fig.10 Vector diagram of gas velocity on plane 1, 2 and 3 after optimization

图11 改进后平面1、2、3上的湍动能分布Fig.11 Turbulent kinetic energy distribution on planes1, 2 and 3 after optimization

综上，对进气口3位置的优化是成功的，优化后剪切机内的气流形态有了很大改善，能促进剪切机内粉尘颗粒的顺利排出和降低剪切刀的损耗速度。

3.3 气固两相模拟结果

根据剪切机实际工作情况，剪切阱附近是产生粉尘颗粒的主要位置，故在气固两相流模型中选取乏燃料剪切阱附近的3处位置进行颗粒注入，注入位置如图13所示。

剪切机内流场中3个平面上稳定后的颗粒体积分数分布的CFX模拟结果示于图14，剪切机内气流流线图和颗粒运动轨迹示于图15，颗粒运动动态模拟的开始-过程-结束3个时间点的截图示于图16。

分析图14可知：平面1上的颗粒主要分布在剪切刀前方位置，平面2和平面3上颗粒主要分布在剪切阱附近。从图15可看出，颗粒均流向溜槽一个出口，符合实际情况。但流体域内局部区域仍存在涡旋，不利于颗粒排出剪切机。从图16可看出，颗粒注入流体域后随气流一起运动。在颗粒运动模拟开始时，每条流线上均有1个颗粒，这些颗粒从颗粒注射位置发出，沿各自的流线开始运动，此时剪切机内的颗粒数最多；在颗粒运动模拟过程中，各条流线上的颗粒沿各自的流线继续运动，其到达的位置处于动态变化，此时一部分颗粒还在剪切机内运动，而另一部分已排出剪切机并进入溶解器，此过程为颗粒的扩散过程，剪切机内的颗粒数逐渐减少；在颗粒运动模拟结束时，各条流线上颗粒到达的位置已稳定，不再发生变化，此时颗粒的扩散结束，剪切机内的颗粒数最少。分析可知，大部分颗粒最终可顺利排出剪切机，只有少部分颗粒留在剪切机内，如图16中红圈所标的颗粒即在剪切机内死角处形成沉积，不能排出剪切机。

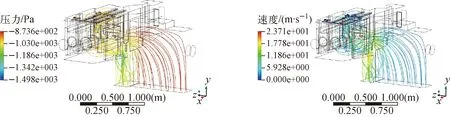
图12 改进后剪切机内气流压力和气流速度流线图Fig.12 Pressure streamline and velocity streamline of gas after optimization

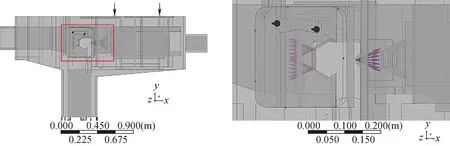
图13 剪切机内颗粒注入位置Fig.13 Particle injection location

图14 平面1、2、3上颗粒体积分数分布 Fig.14 Distribution of particle volume fraction on planes 1, 2 and 3

图15 剪切机内气流流线图(a)和颗粒运动轨迹(b)Fig.15 Airflow streamline diagram (a) and particles trajectory (b)

图16 颗粒运动模拟截图Fig.16 Screenshot of particle motion simulation

3.4 输入条件优化

分析可知，剪切机内流场中颗粒相所占的比重Y与流道尺寸L、进出气口的气流流速v、流量Q和压力p等有关，其函数关系可表示为Y=f(L，v，Q，p，O)，其中，L、v、Q、p、O为独立变量，O表示其他自变量。从纯数学的角度看，这是多约束非线性规划问题，可建立函数模型并通过遗传算法进行求解。考虑到本文研究的剪切机对L、v、Q、p的限制，在其他条件限定不变时，允许进气口1的流速v1可变，因此研究了v1对Y的影响。v1=16、17 m/s时，Y的值分别为1 777和6 094，异常大；v1=18 m/s时风级已达8级，为大风，对剪切机内部器件破坏性较大，故v1不再向后取值。剔除v1=16、17、18 m/s的3个点，通过拟合得到Y与v1的关系，如图17所示。

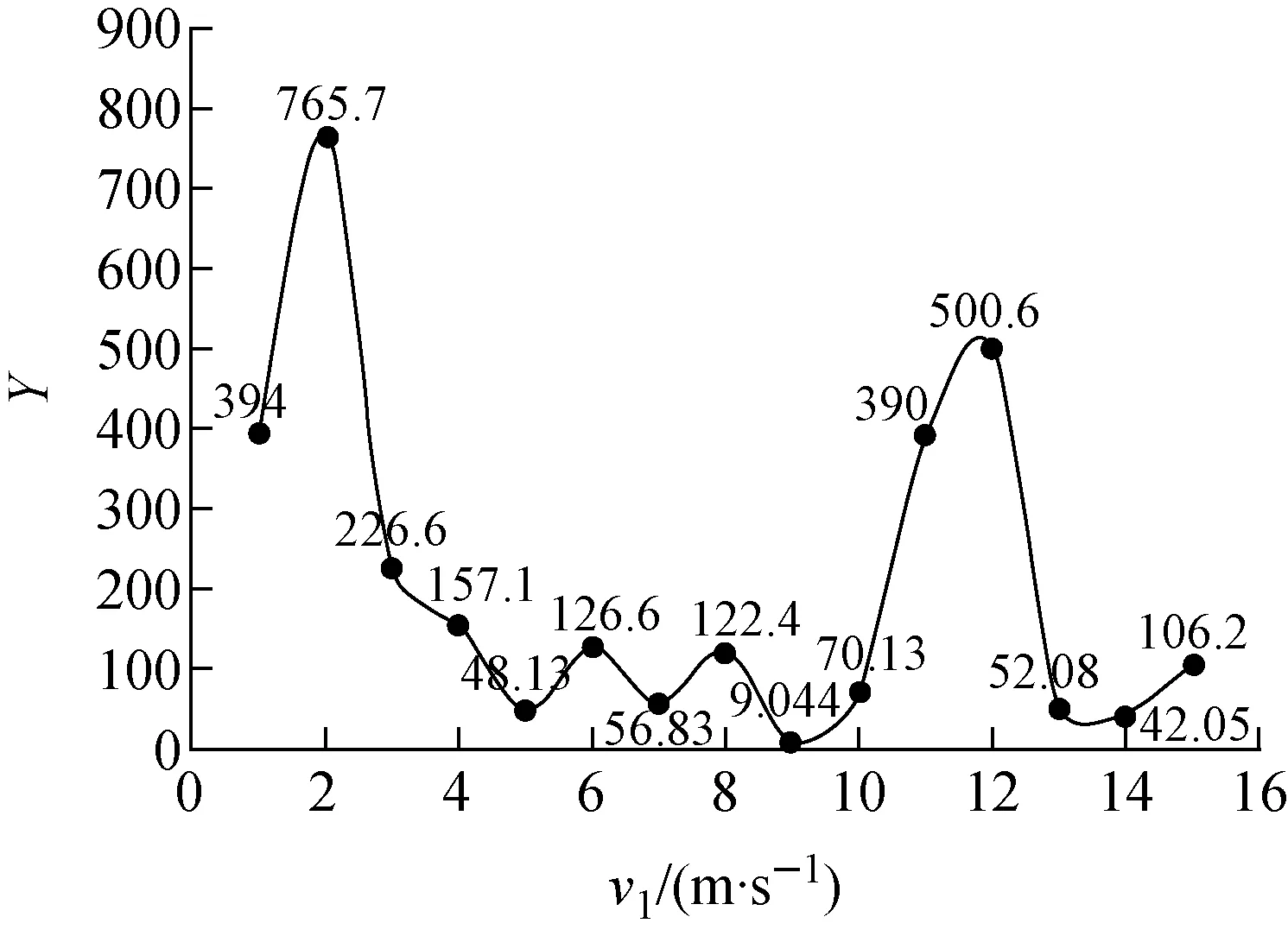
图17 Y与v1的关系Fig.17 Y vs. v1

分析可知，v1=9 m/s时，剪切机内颗粒物浓度水平达到最低值，故在实际工作中可将v1设定为9 m/s，以利于粉尘颗粒排出剪切机。

4 结论

1) 利用CFD软件和数值模拟方法，研究了进气口位置和输入气流流速对剪切机内固体颗粒运动及沉积的影响。进气口位置改进后，剪切机内气相的压力和速度分布得到很大改善，大部分区域速度较均匀，气流路径较为通畅，避免了大涡流的出现；进气口1的气流流速为9 m/s时，剪切机内颗粒物的浓度水平达到最低值。利用同样的方法，可研究气体流量、压力和流道尺寸等对剪切机内流场的影响。

2) 基于欧拉-拉格朗日方法的离散颗粒模型较适用于剪切机内稀相气固两相流的研究。剪切机内的气流是典型的湍流，最大湍流动能出现在速度突变的位置，如剪切机内的死角或有涡流处。剪切机内颗粒物的运动与气流形态密切相关，颗粒的分布与颗粒源的位置以及气流形态密切相关，在颗粒源附近和有涡流的位置，颗粒浓度较高。

对剪切机内气流形态和颗粒物分布运动的模拟研究对于优化剪切机结构和工艺有较强的指导作用，可为剪切机内气流流动和粉尘控制提供理论上的支持。