加速器氚靶膜厚误差对BIXS方法反演的影响

张 哲，张伟光，安 竹，孙洪伟，胡双林

(1.中国工程物理研究院 核物理与化学研究所，四川 绵阳 621900；2.四川大学 原子核科学技术研究所，辐射物理及技术教育部重点实验室，四川 成都 610064)

精确测量氚的含量及深度分布对聚变能源研究、核技术应用和国防建设等领域有重要意义[1]。目前氚分析的方法很多，分为无损分析和有损分析两类[2]。有损分析方法能对整个样品的氚含量和氚深度分布进行分析，但劳动强度大，会产生放射性废物，且不能在线分析，因此在实际应用时受限很大；无损分析方法是通过测量氚β衰变放出的β射线，受β射线能量(平均能量5.6 keV，最大能量18.6 keV)的限制，通常只能进行表面测量。粒子束分析方法的分析深度也受入射能量和深度分辨率的影响，一般为10 μm左右，且不能在线分析。

BIXS(β-ray induced X-ray spectrometry)是日本Matsuyama等[3-6]发展的一项氚无损分析方法，其原理是通过测量β衰变放出的β射线在材料中产生的韧致辐射及特征X射线，来反演得到材料中的氚含量和氚深度分布。由于X射线较β射线更易穿出样品，BIXS方法对金属材料的分析深度可达100 μm左右，对非金属材料分析深度可达1 mm左右。此外，BIXS方法可在线分析。在BIXS方法中，β衰变的内轫致辐射[7-8]、样品表面的粗糙度[8-9]、样品的氚含量[10-11]、测量设备与蒙特卡罗模拟模型的几何尺寸的误差[8-9]、反演的程序[10,12-13]等会影响反演的结果，从而引起氚量和氚深度分布的误差。而蒙特卡罗模拟时的氚靶膜厚与实际的氚靶膜厚的误差也会对反演结果有一定的影响，本文将对此问题开展研究。

1 BIXS方法

BIXS方法[3-6,13-14]是以氚β衰变放出的β射线与样品材料相互作用为理论基础，原理如图1所示。金属氚化物表面吸附层的氚衰变产生的β射线从金属材料表面逃离并与周围的工作气体Ar作用，产生Ar的特征X射线，体相内的氚衰变产生的β射线与含氚材料的原子碰撞，产生连续韧致辐射X射线和特征X射线，通过X射线探测器探测得到X射线总能谱。

将金属含氚物平均分为N层，设每层氚均匀分布，则：

(1)

其中：S(E)为X射线探测器探测得到的X射线能谱；fi(E)为仅第i层含有单位氚量时的X射线能谱，即基函数谱；ai为第i层的氚含量。基于蒙特卡罗方法程序PENELOPE可模拟得到每层的fi(E)，通过反演计算得到的ai便是氚含量和氚深度分布。由于fi(E)所组成的矩阵条件数很大，式(1)是1个病态问题，即原始数据在经典意义下的近似解不存在，或原始数据微小的扰动导致计算结果剧烈变化。Tikhonov正则化法是一种具有完备理论的用来解决病态反演问题的方法，基于蒙特卡罗模拟和Tikhonov正则化方法，BIXS方法可对样品的氚含量和氚深度分布进行可靠分析。由于蒙特卡罗方法的灵活性，这种方法适用于较复杂的实际情况。此外，如果氚靶膜厚未知，则无法分层，也就无法模拟基函数谱，因此目前BIXS方法不适用于未知靶膜的氚含量。

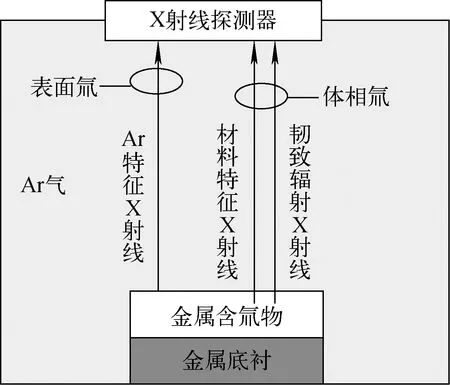
图1 BIXS方法基本原理Fig.1 Basic principle of BIXS method

2 结果与讨论

2.1 模拟实验结果与分析

依据控制变量法设计模拟实验，在其他建模条件(如几何模型、反演的条件、氚靶靶膜的氚浓度分布等)不变的情况下，仅改变模拟时的氚靶膜厚，将反演的氚量与理论计算的氚量比较，以此得到膜厚误差对BIXS方法反演的影响。

本文的氚靶靶膜是钛膜，以某一厚度的靶膜为基准，将靶膜均匀分为10层，基于蒙特卡罗模拟程序PENELOPE，模拟得到每层的反演基函数谱fi(E)，如图2所示。氚在靶膜中有4类典型的分布：递减分布、递增分布、均匀分布和正态分布[10]，本文对此4种分布分别进行模拟实验。以基准厚度含氚靶膜为基准，以2%为阶梯，上、下各模拟3种厚度含氚靶膜的基函数谱，根据基函数谱构造4种氚分布情况下的X射线能谱，如图3所示。

设定反演的相关条件后，依据基准厚度含

氚靶膜的X射线能谱和基函数谱，可反演得到其氚量，设此氚量为基准氚量。基于4种氚深度分布函数和膜厚易计算出其他6种厚度的理论氚量，依据其他6种厚度靶膜的X射线能谱和基准厚度含氚靶膜的基函数谱，可反演得到对应的反演氚量，反演氚量相对于理论氚量的误差就是要寻求的影响结果，其结果列于表1。

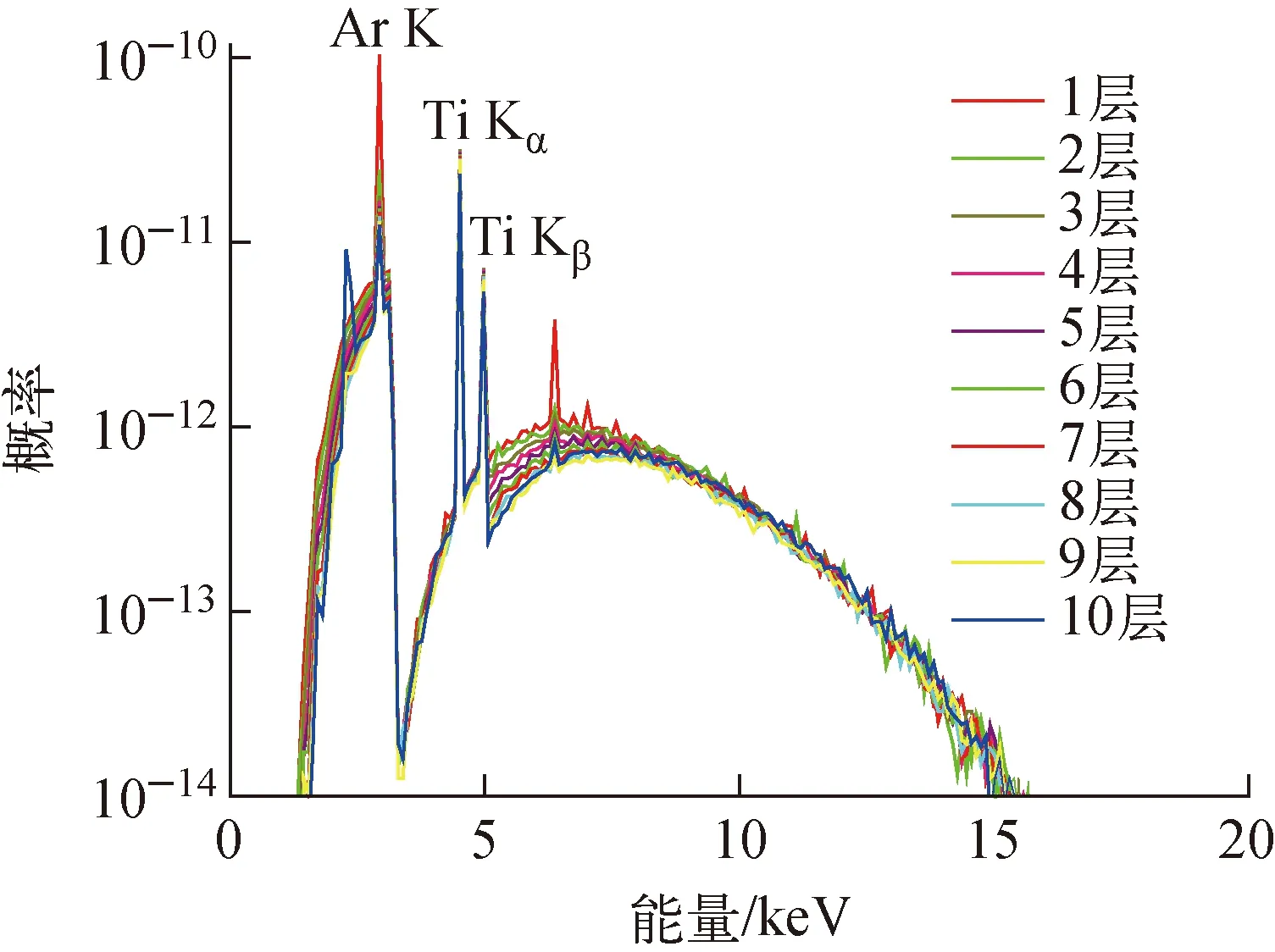
图2 基准厚度含氚靶膜的基函数谱Fig.2 Basic function spectrum of tritium film with base thickness

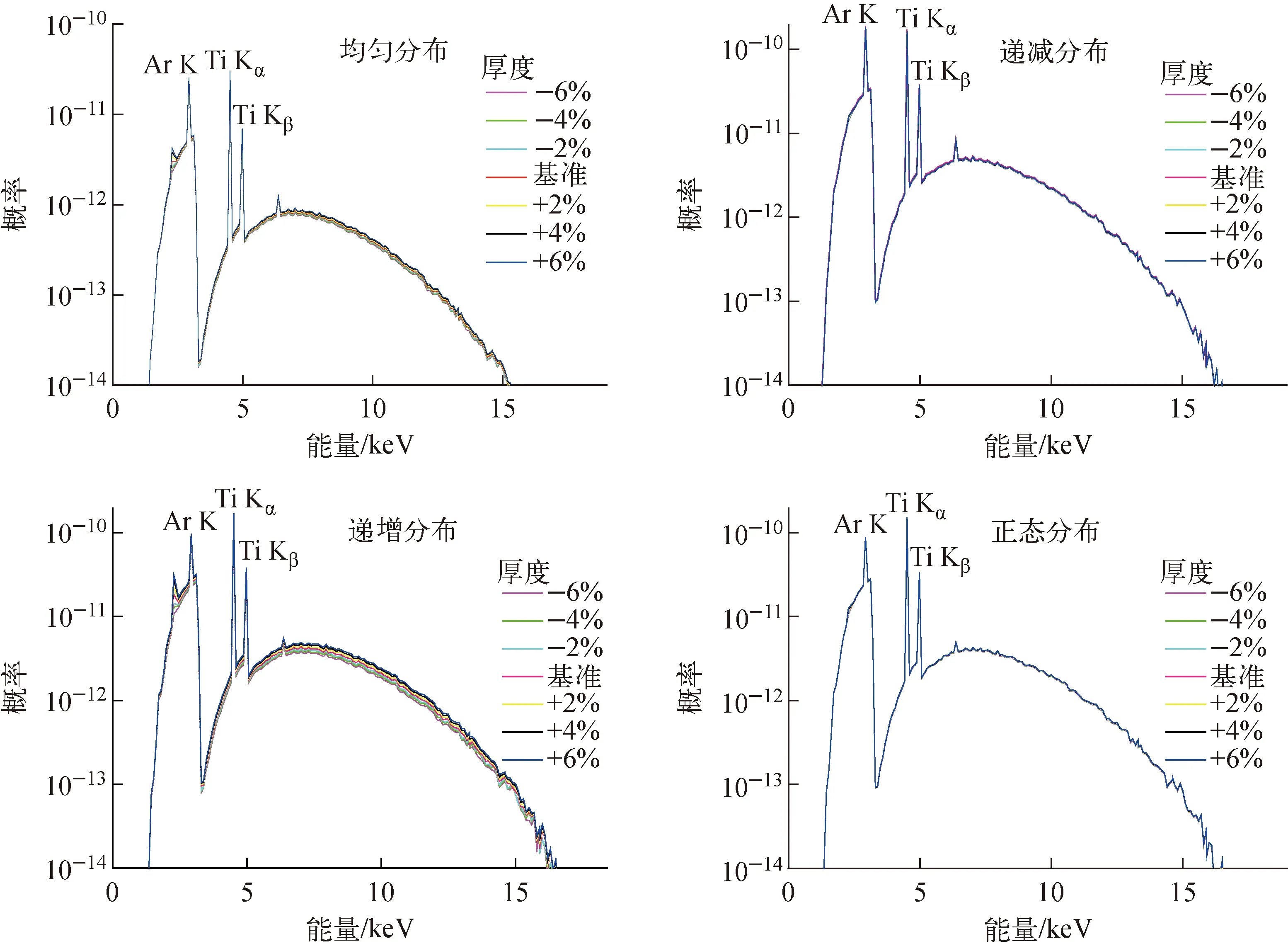
图3 4种氚分布的不同厚度靶膜的X射线能谱Fig.3 X-ray spectrometry of tritium film of four kinds of tritium distributions with different thicknesses

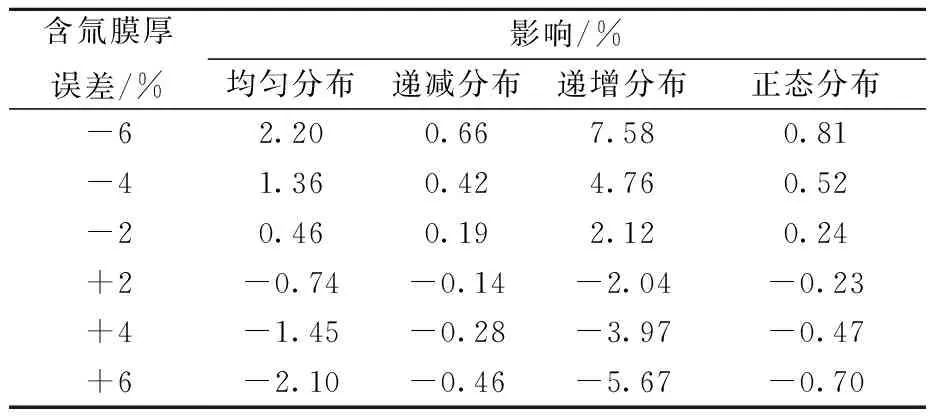
表1 4种氚分布情况下不同膜厚误差对BIXS方法反演的影响Table 1 Effect of different thicknesses error of tritium films with four kinds of tritium distributionson inversion of BIXS method

由表1可知，膜厚误差对氚递增分布的BIXS方法反演影响最大，对氚递减分布的影响最小。其原因由图3可知，递增分布时膜厚误差导致的X射线能谱差别相对最大，而递减分布时膜厚误差导致的X射线能谱差别相对最小。由文献[14]可知，BIXS方法测氚总量与PVT方法[15]测氚总量符合很好，两种方法的相对误差在5%以内，因此膜厚误差是不可忽视的一个因素，尤其是对氚递增分布的靶膜。

2.2 实验结果与分析

模拟实验是在基函数谱fi(E)厚度不变的情况下通过改变模拟谱S(E)的厚度来分析，实验验证是在实验谱S(E)不变的情况下通过改变基函数谱fi(E)的厚度来分析。

实验选取4种膜厚的氚靶，厚度的测量采用称重法，测量仪器是绝对精度为0.001 mg的百万分之一电子天平，在相同充氚工艺下充氚，尽量使氚靶的氚量一致，数据处理时对厚度和氚量进行归一化处理。基于高纯锗探测器测量4种厚度氚靶的X射线能谱，基于PENELOPE程序模拟4种厚度氚靶的基函数谱，其中1#靶反演时的BIXS拟合谱如图4所示。

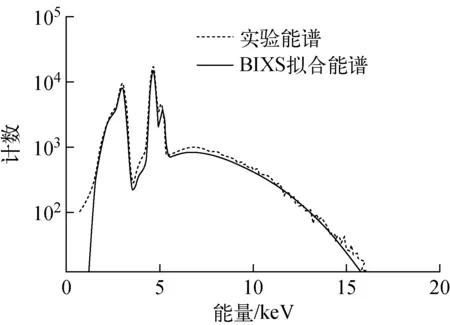
图4 1#靶的BIXS拟合能谱Fig.4 X-ray fit spectrum of BIXS of 1# target

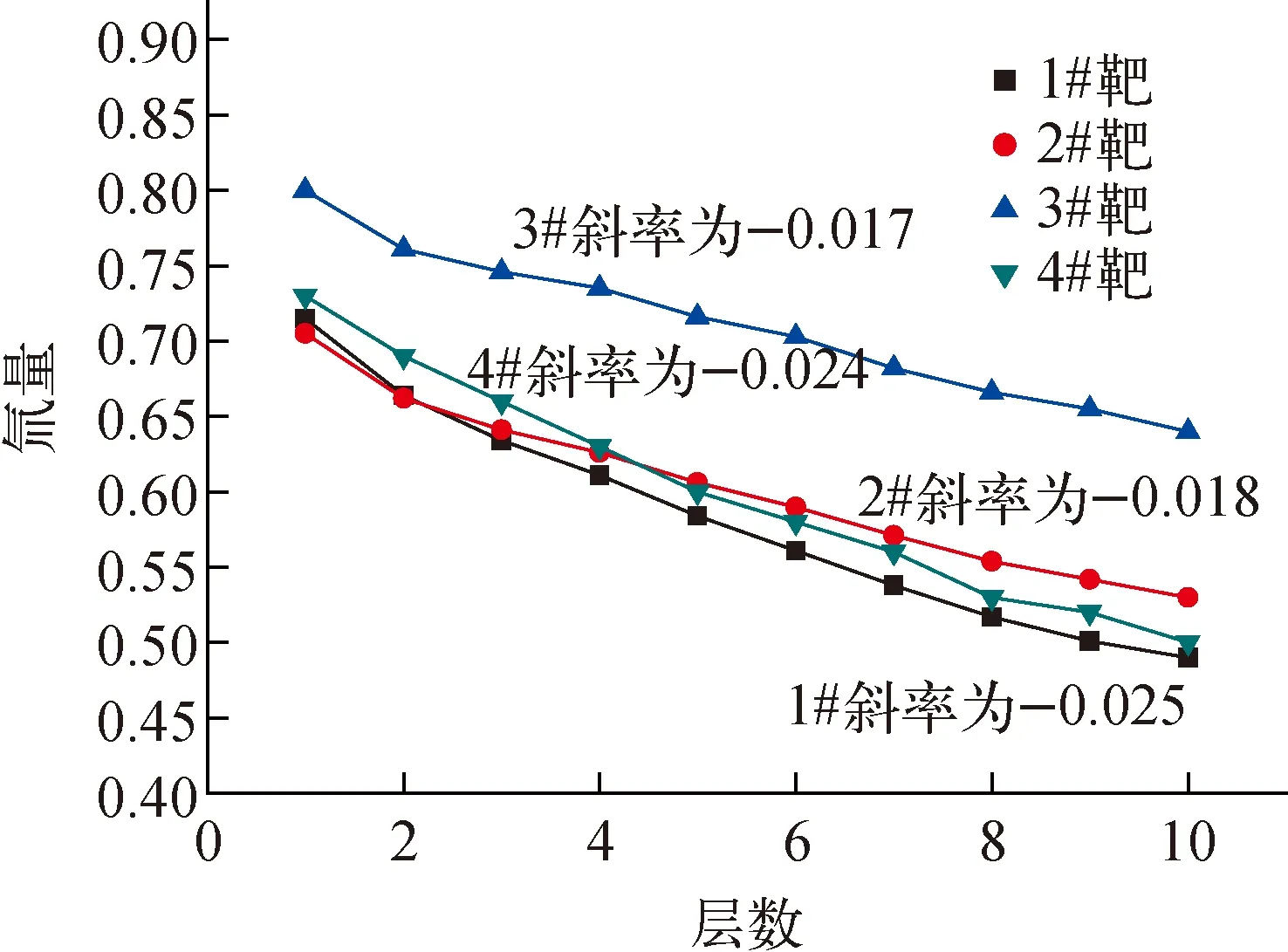
图5 氚的深度分布Fig.5 Tritium depth distribution

通过BIXS方法反演得到的4个靶的深度分布如图5所示，其中的氚量是氚含量相对值，3#靶的氚量相对较大。由图5可知，4个靶的氚深度分布均是递减分布，将4个靶的深度分布进行线性拟合，可知4个靶的斜率大致相当，2#靶和3#靶的斜率稍大些。BIXS方法反演结果与PVT方法的结果列于表2，其中3#靶的氚量相对较高，这与张伟光等[14]的结论一致，即BIXS方法反演的结果与PVT方法的结果一致，两者的相对偏差平均在5%左右。

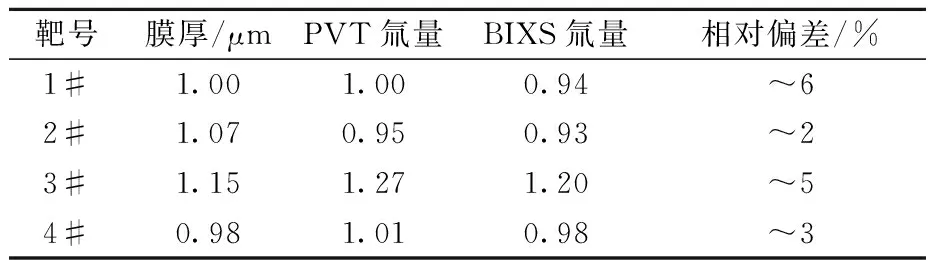
表2 BIXS方法反演结果Table 2 Inversion outcomes of BIXS method

在4个实验靶的实验谱S(E)不变的情况下，通过改变基函数谱fi(E)的厚度误差来分析膜厚误差对BIXS方法反演的影响，计算时以基准厚度的基函数谱反演氚量为基准，其他厚度基函数谱的反演氚量与该反演氚量相比较，其结果列于表3。

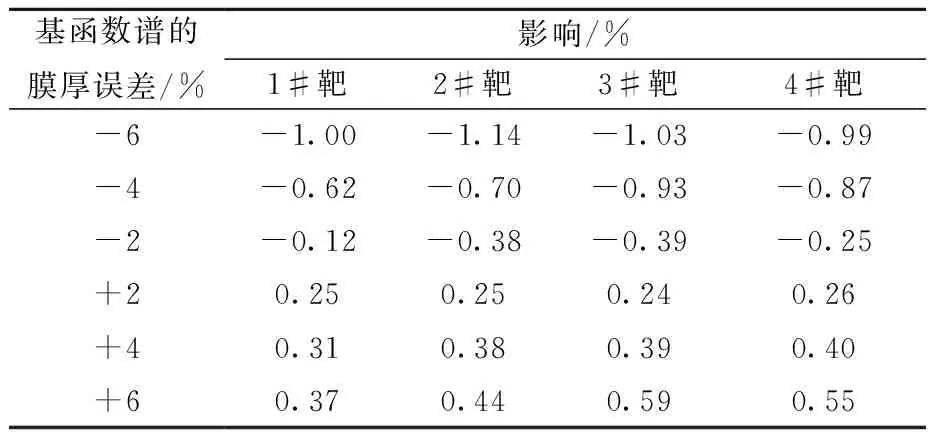
表3 基函数谱的膜厚误差对BIXS方法反演的影响Table 3 Effect of film thickness error of basic function spectrum on inversion of BIXS method

从表3可知，当氚的深度分布为递减分布、基函数谱的膜厚与含氚靶膜的厚度误差为-6%时，对BIXS方法反演造成的影响为：1#和4#靶的实验结果均为1%左右，2#靶的实验结果为1.14%，原因是2#靶的斜率较大；2#和3#靶的斜率相近，而3#靶实验结果也为1%左右，其原因是3#靶的氚量相对较大。在其他条件(如样品的氚量和表面的粗糙度、建模几何尺寸的误差、反演的程序等)一致的情况下，在相同的膜厚误差下，斜率越大，导致的BIXS方法反演的氚量的误差也越大。从表1也可看出，递减分布、均匀分布和递增分布的斜率逐渐变大，对BIXS方法反演的影响也逐渐变大，其中递减分布的斜率为负数，均匀分布的斜率为0，递增分布的斜率为正数；斜率越大，膜厚误差对BIXS方法反演造成的影响就越大。

3 结论

本文基于蒙特卡罗模拟程序PENELOPE，模拟分析4种典型的氚在靶膜中分布的基函数谱和X射线能谱，通过对比反演氚量和理论氚量的误差可知，膜厚误差对BIXS方法反演的影响不可忽视，其中对氚递增分布的影响最大，对氚递减分布的影响最小，这是因为递增分布时膜厚误差导致的X射线能谱差别相对最大，而递减分布时膜厚误差导致的X射线能谱差别相对最小。通过实验结果并结合模拟实验结果的分析可知，氚在靶膜中的3种深度分布，即递减分布、均匀分布和递增分布的斜率逐渐变大，斜率越大，膜厚误差对BIXS方法反演造成的影响就越大。

在基于BIXS方法测量含氚靶靶膜的氚量时，需膜厚的数据，对于未知膜厚的含氚靶，目前的BIXS方法无法适用，本文对于该问题的研究有一定的指导意义。