关于一元非线性回归的一个经验模型

谢黎东

(新疆水利水电学校 新疆乌鲁木齐 830013)

对这类指数函数型回归问题和幂函数型回归问题，传统方法是对其取对数，将它化成线性函数，接下来求出线性关系中的参数，然后通过逆变换求出原函数中的参数。笔者认为，在线性关系中，变量x'，Y'是否有显著的相关性，应首先进行检验，只有当x'，Y'有显著的相关性时，求出的线性回归方程才有意义，此时求得的参数也才有意义，通过逆变换求得的原函数的参数才有实际价值。

一、基本方法

基于线性关系，关于变量x'，Y'得到一组新数据。

如果︱r︱＞r0.05（或r0.01），就称变量x'，Y'有显著的相关性（或高度的相关性）。

若想求出该方程组的解非常困难，缺乏操作性。

为此，将已经求出的（A）式代入（1）式就得到

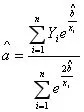
二、简易模型

从上述基本方法，不难得出下面的经验模型

即

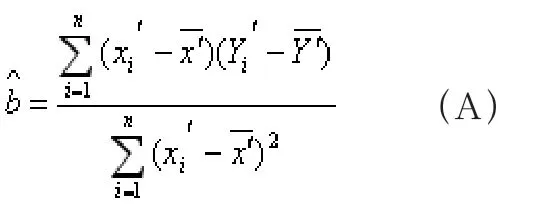
以该模型求得的回归曲线，其拟合效果也好于传统方法（可以验证）。

三、实例分析

炼钢厂出钢时所用盛钢水的钢包的容积，由于钢液和钢渣对钢包衬耐火材料的侵蚀，随着使用次数的增多而增大，为了求出使用次数和增大容积之间的定量关系式，现测得此样如下表所列，其中使用次数为，增大容积是。试求增大容积Y关于使用次数x的回归方程。

表1

解：作散点图，在散点图上画一条光滑曲线，由曲线形状看出，可能是

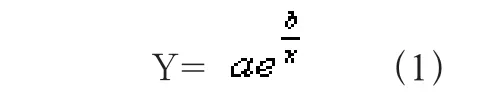
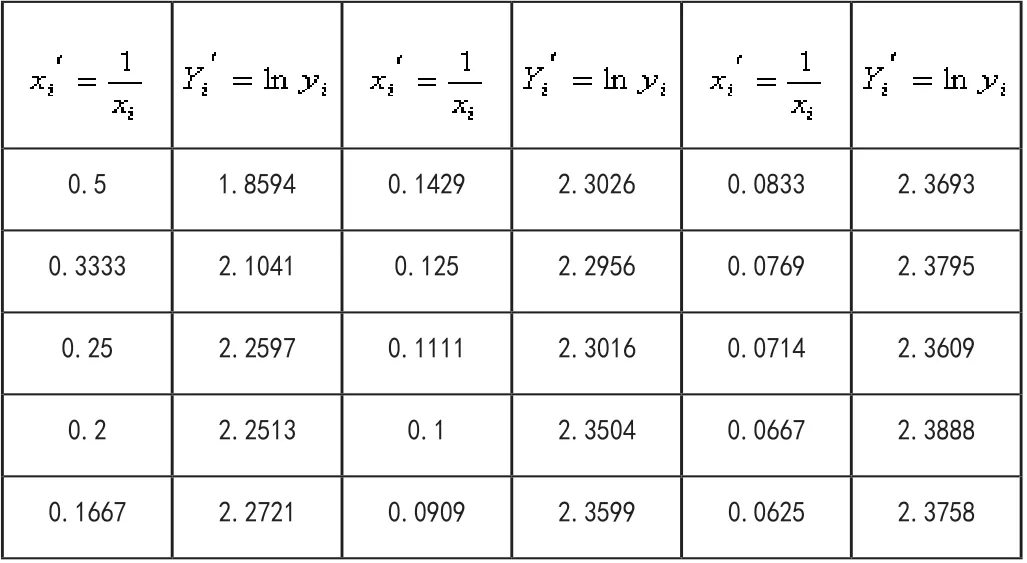
表2

按一元线性回归计算

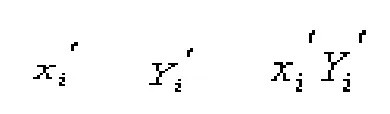
∑ 2.3807 34.231 0.5842 78.3844 5.2027

检验变量x'，Y'的线性相关性，计算

|r|＞r0.01=0.641，变量x'，Y'有高度相关性

对比看出，按本文经验模型求出的回归曲线，其拟合效果好于传统方法。

四、结束语

本文所总结的经验模型，计算方便，简单实用，操作性强，在实际计算中对指数函数型回归问题和幂函数型回归问题，均可以使用本文提供的这一模型。