可再充填起动篮芯柱结构排气管流体传输规律与仿真

单立杰，宁继荣，肖明杰

(西安航天动力研究所，陕西 西安 710100)

0 引言

表面张力贮箱是多次起动液体火箭动力系统贮箱的重要类型。安装于贮箱内部的推进剂管理装置(PMD)利用推进剂与多孔毛细元件或板片相接触的表面张力作用维持液、气分离，实现复杂过载条件下推进剂不夹气供应，具有无活动部件，可靠性高，相容性好，可重复使用等特点，在各种航天器动力系统上应用广泛[1-3]。

起动篮是一种典型的表面张力推进剂管理装置，其主要用于多次起动推进剂管理。起动篮是由筛网或多孔板等多孔毛细元件组成的封闭结构，可单独安装于贮箱底部，也可以结合贮箱壳体组成封闭容腔。起动篮分为不可再充填和可再充填两种类型，其基本结构如图1所示，是否具有排气管结构是两种起动篮的主要区别。

不可再充填起动篮向下游发动机供应推进剂实现发动机起动后，气体替代篮内的推进剂，蓄留在其中且不能排出，只能用于有限次、有限推进剂耗量的起动。而可再充填起动篮顶端设置有排气管，能利用发动机点火产生的沉底加速度，在供液过程中将气体从篮内排出实现再充填，用于发动机下一次起动，任务适应性更广泛。

国外NASA Lewis研究中心在进行Centaur D-1s研究时，提出了可再充填起动篮推进剂管理和热控方案，并与其他方案进行了比较，重点进行了可再充填起动篮再充填方面的研究[4]。Martin Marietta公司也曾开展了可再充填起动篮原理样机研究工作[5]。国内西安航天动力研究所结合多孔毛细元件气液隔离机理及气液界面稳定准则，建立了可再充填起动篮再充填过程模型并通过了地面试验验证，将可再充填起动篮成功应用于某大流量泵压式发动机上面级，解决了大起动耗量与多起动次数、小管理容积矛盾下的推进剂管理难题[6]。

在微重力或较小干扰加速度下实现推进剂自保持，是可再充填起动篮设计重点关注的问题之一。若工作过程中，可再充填起动篮排气管顶端多孔毛细元件不被推进剂湿润，将破坏起动篮的推进剂保持性能，可能引起供应的推进剂夹气，导致发动机工作异常。Martin Marietta公司相关文献中提出了排气管中设置芯柱结构的解决方案，但未见详细分析及具体设计。

本文阐述了可再充填起动篮基本工作原理，对两种典型工况下排气管顶端多孔毛细元件湿润问题进行了分析。针对该问题，基于微重力流体力学与内角自流相关理论，给出了排气管内芯柱结构详细设计方案，并使用FLOW-3D软件对两种典型工况下排气管内流体传输过程进行了仿真分析，研究了带芯柱排气管内流体传输规律，验证了设计方案的正确性。

1 可再充填起动篮工作原理及问题描述

在多孔毛细元件表面，浸润液体会润湿形成液膜。当气液界面两侧存在一定压差时，微观上各个孔隙上的气液界面将呈曲面形状，液膜将阻止气体穿过元件，如图2所示。

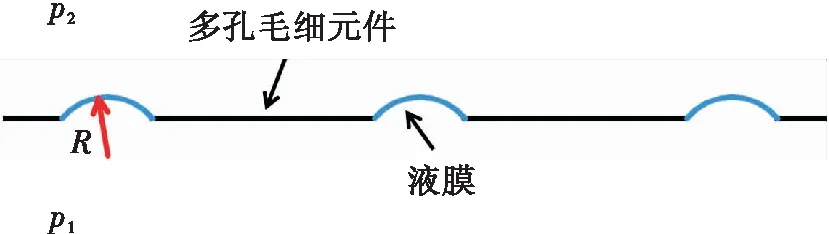
图2 多孔毛细元件原理示意图Fig.2 Schematic diagram of capillary element

若液膜曲面的主曲率半径为R1，R2，其与液膜两侧压差为

Δp=p1-p2=σ(1/R1+1/R2)

式中σ为液膜介质的表面张力系数。多孔毛细元件的液膜所能承受的最大压差称为泡破点，其值通常通过实验进行确定。只要润湿多孔毛细元件两侧压差低于对应的泡破点，气体就不能穿过毛细元件，从而实现气液分离。这是起动篮工作的基础。

根据图3所示的结构来说明可再充填起动篮(以下简称“起动篮”)在不同加速度下推进剂保持和再充填的工作原理。将排气管顶端多孔毛细元件称为元件1，侧面篮网和顶面篮网称为元件2。一般元件1比元件2孔径大，泡破点低。aa、ae、al分别表示反向加速度、沉底加速度和侧向加速度，ha和hl是决定作用在元件1和元件2上的气液压差的相关设计高度。

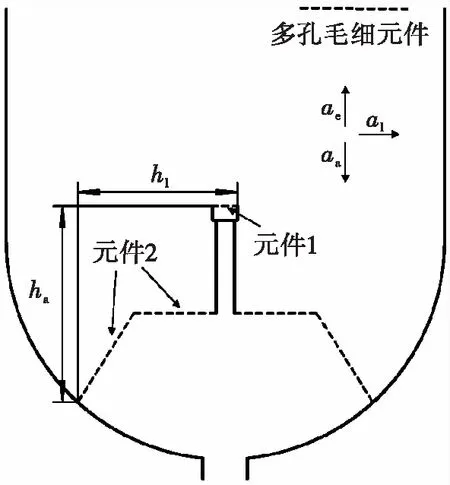
图3 可再充填起动篮结构Fig.3 Structure of refillable start-basket

当存在反向加速度aa时，篮内充填满推进剂，篮外推进剂在加速度作用下沉积在远离起动篮的贮箱内部另一端。要实现起动篮内部推进剂的保持，要求元件2的泡破点Δpc2>ρaaha。反向加速度下，对于元件1，沿着其截面的压差为0，很容易实现气液界面的稳定。

当存在侧向加速度al时，篮内充填满推进剂，篮外推进剂沉积在与侧向加速度相反的贮箱壁面一侧。为了实现起动篮内部推进剂的保持，要求元件1的泡破点Δpc1>ρalhl。当发动机工作时，存在沉底加速度Ae，篮内气体最大高度为ha，为了使气体击穿元件1从而实现再充填，要求推进剂静压差大于元件1泡破点，即Δpc1<ρaeha。沉底加速度下再充填过程，贮箱出口流量小于一定值，由液面高度ha产生的推进剂静压差克服液体过网流阻及元件1泡破点，篮外推进剂自元件2进入篮内，篮内气体经元件1排出篮外。随着起动篮内部液面的上升，ha逐渐减小。

对于元件1，为了满足推进剂自保持，泡破点值尽可能高；而为了实现再充填排气，其泡破点值又不宜过高。起动篮设计过程需根据全任务剖面各向加速度变化情况针对该矛盾问题进行最佳平衡，寻求最优设计方案，以保证起动篮既可以实现推进剂保持，也能实现可靠再充填。

如前所述，再充填末期，随着篮内液面上升，ha逐渐减小，当静压差ρaeha低于元件1泡破点Δpc1时，剩余气体将无法击穿元件1而残留在排气管中，具体如图4所示。

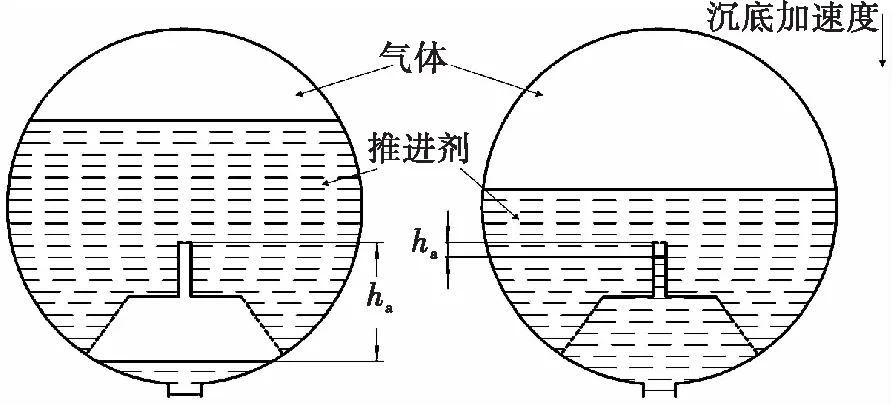
图4 起动篮的再充填过程Fig.4 Refilling process of refillable start-basket

如图5所示，在工作后期贮箱内推进剂剩余量较少时，推进剂液面在沉底状态下将低于排气管顶端，对于泡破点较小的排气管顶端多孔元件，不能保持湿润的风险将大大增加。

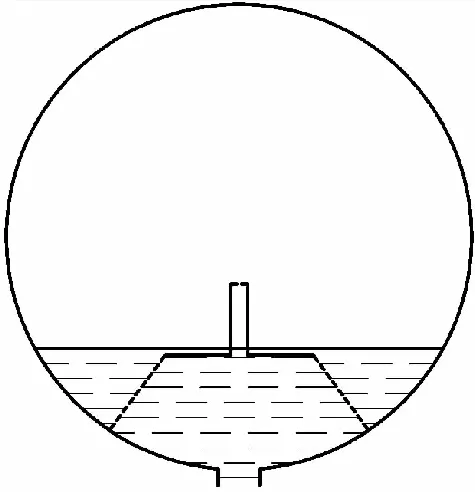
图5 起动篮工作末期液面状态Fig.5 Liquid state at the end of the start-basket

排气管内部残存有气体以及排气管顶端暴露于气体中，有可能导致多孔毛细元件不再湿润，从而不具备气液隔离功能。如图6所示，在侧向加速度条件下，气体自排气管顶端的多孔毛细元件进入，并将推进剂从起动篮内排出，起动篮丧失介质保持功能。

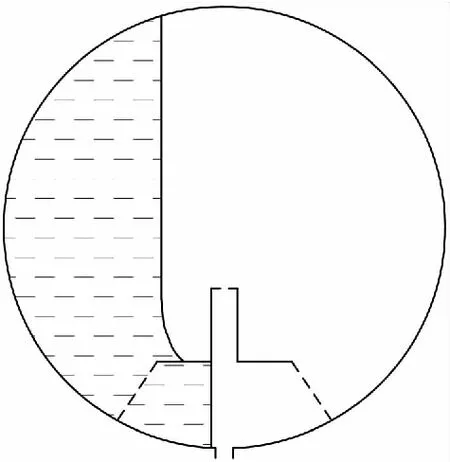
图6 推进剂在侧向加速度作用下泄漏Fig.6 Propellant leaks under lateral acceleration

根据上述分析可见，保持元件1持续湿润，是提高起动篮工作可靠性的切实要求，有必要进行相应设计，提高起动篮全任务剖面工作可靠性。

2 排气管芯柱技术方案

2.1 理论分析

如图7所示，固体、气体、液体共同接触的界面上，液体以特定的角度与固体表面相接触，此角称为接触角，用θ表示。

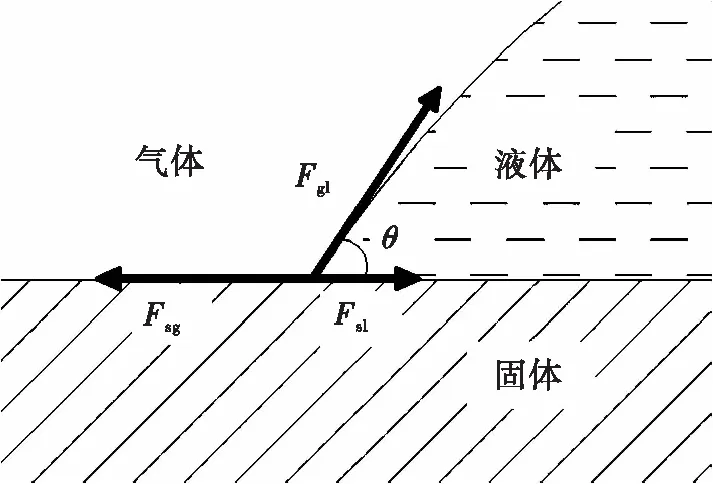
图7 液-固-气界面示意图Fig.7 Schematic diagram of liquid-solid-gas interface

图7中Fgl是气液界面上的界面张力；Fsg和Fsl分别为气固界面和固液界面上的界面张力。它们之间满足Young方程

Fglcosθ=Fsg-Fsl

接触角θ仅与固体和液体的性质有关，当其处于0到π/2之间时，固体表面分子对液体分子的吸引力比液体分子自身吸引力要强得多[7-9]，液体将沿着固体表面进行铺展，称液体对该固体表面是润湿的。

仅靠液体的润湿特性，排气管内液面距离多孔毛细元件有一定距离时，无法保证其湿润多孔毛细元件。对排气管内蓄有部分推进剂时，气液界面变化情况进行仿真。排气管内径取30 mm，推进剂为绿色四氧化二氮，参数如表1所示。接触角θ取0，过载取1×10-5m/s2，方向向下。

表1 绿色四氧化二氮相关参数Tab.1 Parameters of green nitrogen tetroxide

图8为气液界面变化仿真结果。可以看到稳定后气液界面呈曲面状，液体中心凹陷。虽然与壁面接触的推进剂能爬升一定高度，但由于排气管直径比一般毛细效应的尺度大，推进剂爬升高度和效率难以保证顶端的多孔元件保持润湿状态。

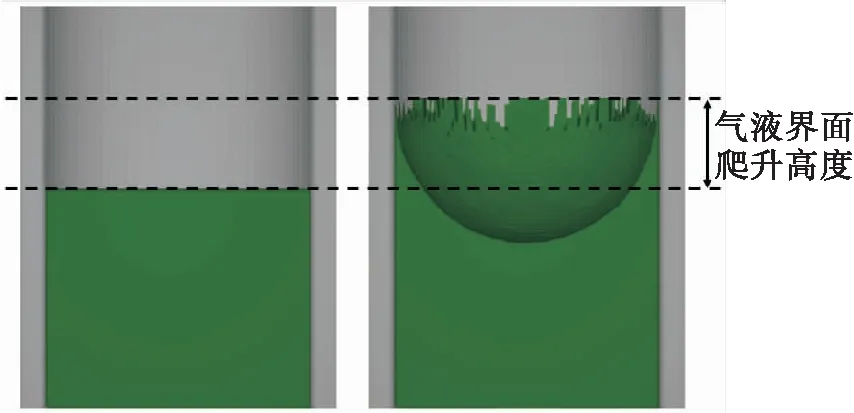
图8 气液界面的变化Fig.8 Change of gas-liquid interface

利用液体的浸润特性，可使用非活动部件对液体行为进行控制，实现导流效果。图9中液体可沿固体壁面爬升，是由于固体壁面存在夹角而引发的内角自流(Interior Corner Flow)现象[10-14]。维持液体沿夹角流动的驱动压差，来自于沿流动方向上逐渐减小的流动截面面积。

根据动力学理论关系式，紧靠表面分子的主体分子交换时间为

t=l2/Cd

式中：Cd为扩散系数；l为晶格间距。以水为例进行计算，可得其交换时间处于10-10s数量级，与流动时间相比，该时间可以忽略不计。因此达到表面张力平衡所需的时间极短，在对内角自流进行分析时，可以认为垂直于流动方向上的任一截面，气液界面均处于力学平衡状态，整个内角自流过程可以当做一系列连续的力学平衡过程进行处理。在该假设下，就可以使用Young-Laplace方程，建立液体流动方向上的液体内部压强和气液界面几何外形之间的关系。

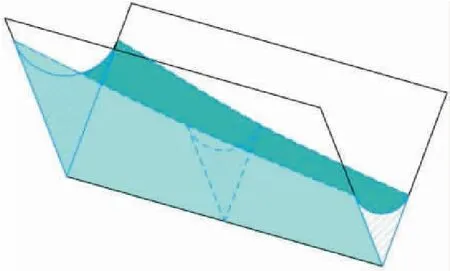
图9 内角自流现象Fig.9 Interior corner flow

图10给出了垂直于流动方向上的流动截面示意图，其中2α为壁面夹角；θ为液体与壁面接触角；r为气液界面的曲率半径；D为单侧壁面的润湿长度；δ为气液界面夹角半角。

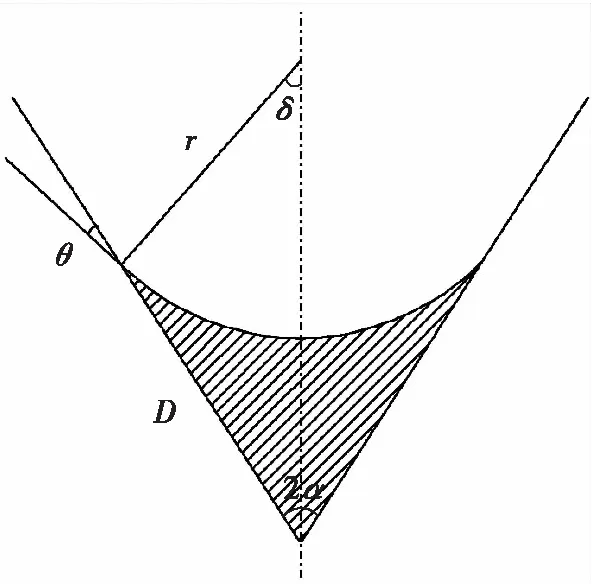
图10 流动截面示意图Fig.10 Fluid cross-section diagram

根据几何关系，流动截面面积S满足

联立方程组，可得

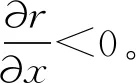
相比于界面方向，沿流动方向上的气液界面曲率半径近似于无穷大，则在任一流动截面上，Young-Laplace方程简化为

将该式两侧对x进行求导，并且将气体压强当做常量处理，可得

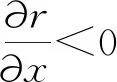
利用具有夹角的部件可实现液体导流的分析结论，可以在排气管内设置芯柱结构导流组件，对排气管内液体行为进行干预和控制，将液体从底部液池导向排气管顶端，保持顶端多孔毛细元件湿润。毛细作用下液体沿着多孔毛细元件的铺开湿润是显见的，本文不作赘述。

在具体工程设计中，使用变分法并引入Weislogel无量纲流阻，可以得到内角自流控制方程的自相似解。进而得出相关任务剖面的芯柱总导流量、导流效率等相关参数与芯柱设计参数之间的关系，完成芯柱的设计和优化[15-16]。

2.2 设计方案

某起动篮表面张力贮箱设计方案如图11所示，贮箱由壳体和起动篮组成。

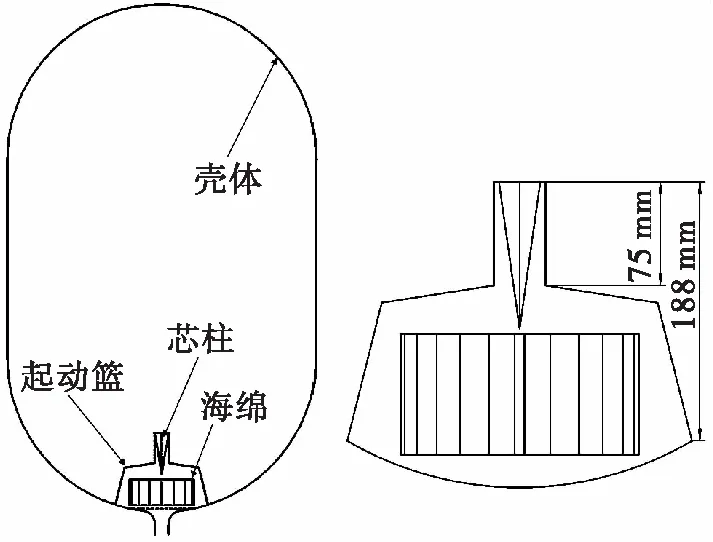
图11 贮箱及起动篮结构简图Fig.11 Schematic diagram of tank and start-basket

篮内使用海绵管理装置进行推进剂定位，以确保起动篮内部进气后推进剂蓄留在海绵内，从而提高工作可靠性[17]。排气管内设置芯柱，芯柱由锥形十字导流板构成，在排气管中以锥角向下的方式放置。起动篮及其内部海绵、排气管及芯柱三维示意如图12所示。

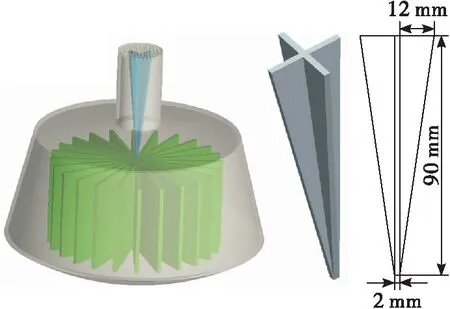
图12 起动篮及芯柱结构Fig.12 Structure of start-basket and core

贮箱容积约600 L，发动机在轨起动9次，单次起动推进剂耗量约2 L，沉底加速度由0.14g增加到0.2g，起动篮容积为5 L，滑行阶段微重力环境为1×10-5g。

以氧化剂绿色四氧化二氮为例计算典型工况。根据第1章中的分析，沉底加速度越小，再充填结束后存留在篮内的气体越多。已知排气管顶端元件1泡破点为120 Pa，第一种典型工况是在最小(初始)沉底加速度下，存留在排气管内的气体高度约为30 mm；第二种典型工况是在发动机第8次长程工作结束后，贮箱内剩余推进剂液面将低于排气管20 mm，在该情况下，所设计芯柱将浸入推进剂内5 mm，如图13所示。

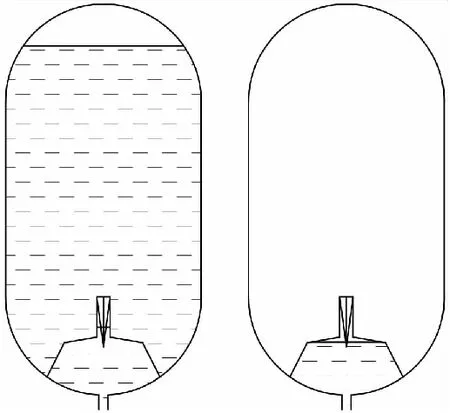
图13 典型工况Fig.13 Typical case

对两种典型工况进行仿真，验证芯柱能将篮内推进剂抽吸导流至排气管顶端，解决排气管顶端毛细元件的持续润湿问题。

3 数值仿真与结果

3.1 计算模型

考虑到实际工作状态，在求解过程中，推进剂视为黏性不可压缩流体，且不考虑传热、相变的影响，聚焦于惯性力、黏性力和表面张力对液体行为的影响。因此计算模型涉及到不可压连续方程、动量方程、表面张力相关方程等。

对于这类求解在微重力条件下液体行为的问题，FLOW-3D软件因具备泛用的物理模型并整合了完善的处理工具而被广泛应用。

在FLOW-3D中选取重力和非惯性参考系模型、表面张力模型、黏性和湍流模型等并进行相关调试建立了计算模型。为验证其合理性，针对已有的大叶片板式贮箱中液体行为分析算例[18-20]进行了仿真，与对应的仿真和实验结果进行对比，该算例中，所用液体介质为水。结果如图14所示。图14(a)是已有的仿真和实验结果，图14(b)是使用构建的计算模型所完成的仿真结果。

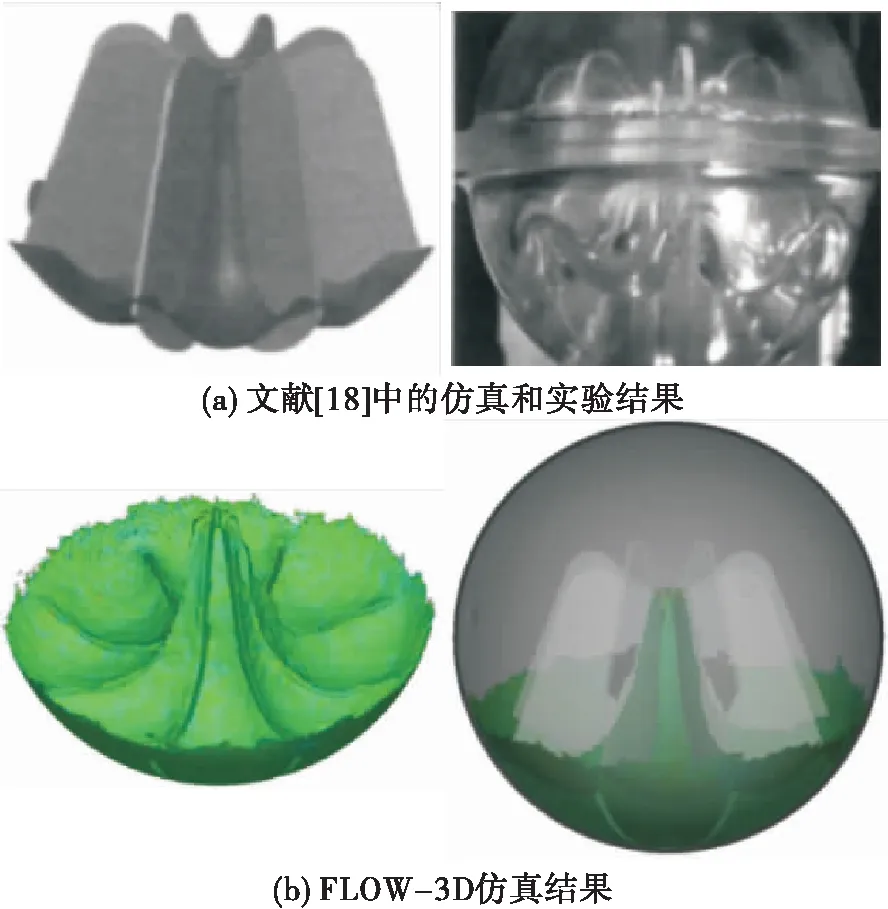
图14 叶片式贮箱内液体行为仿真结果对比Fig.14 Comparioin of simulation results of liquid behavior in vaned tank

经过对比，使用计算模型仿真得到的结果与文献中的实验结果基本吻合，故认为模型合理正确，可用于对芯柱性能的验证。

针对2.2节中所提出的两种典型工况所构建的三维模型和起动篮内推进剂液面位置如图15所示。

图15 起动篮三维模型及初始液面位置Fig.15 3D model of start-basket and initial liquid position

为了使FLOW-3D软件能正确地识别计算模型，同时节约资源和时间，对壁厚向外进行了扩增。网格精度取1 mm，比固体壁面最薄厚度低2/3以上，以精确捕捉芯柱的外形特征。排气管顶端边界条件设置为Outflow，其他设置为Wall。

3.2 仿真结果

针对第一种工况进行数值仿真的结果如图16所示，图16中推进剂区域的颜色表明了其在z轴正方向上的速度分量，即推进剂的爬升速度。根据图示，推进剂可以在1.16 s爬升至排气管顶端。

在初始阶段，推进剂对固体壁面的浸润特性使其沿芯柱和排气管内壁进行铺展，而芯柱夹角位置处的表面张力作用更强，因此该处推进剂爬升速率比其他位置的明显要高。随着运动逐渐进行，气液界面由平面向弯月面进行发展，芯柱所导流的推进剂沿流动方向上流动截面逐渐减小，具有稳定的内角自流驱动压差，维持推进剂的持续爬升，最终到达了排气管顶端位置。

第一种工况的仿真结果表明，篮内推进剂液面位于排气管内时，芯柱可以有效维持排气管顶部的湿润。

第二种工况的仿真结果如图17所示。

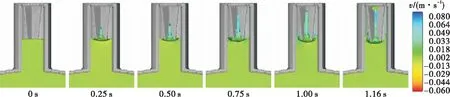
图16 第一种工况仿真结果Fig.16 Simulation results of the first case

图17 第二种工况仿真结果Fig.17 Simulation results of the second case

可以看到，推进剂可以在1.8 s内爬升至排气管顶端。

在表面张力作用下，推进剂沿着固体壁面进行浸润运动，主要分为两部分，沿芯柱引流片夹角向排气管顶端运动，以及沿着起动篮上壁面铺展运动。随着时间逐渐增长，推进剂在芯柱导流的作用下向上运动形成凸起，与芯柱接触的推进剂曲率下端半径较大，而上端曲率半径小，能为推进剂沿芯柱的流动提供驱动压强。而与壁面相接触推进剂的运动也带动气液界面逐渐向中间包裹。在这两部分运动的共同作用下，液池中形成了介于二者之间的环形空腔。图18给出了0.1 s和0.7 s时气液界面的速度矢量图。图18中，红色为液体区域，蓝色为气体区域，白色箭头表征速度矢量。可以看到初始阶段液体凸起的形成，以及由于推进剂沿芯柱的流动与沿壁面的铺展这两部分运动而导致环形空腔的形成。

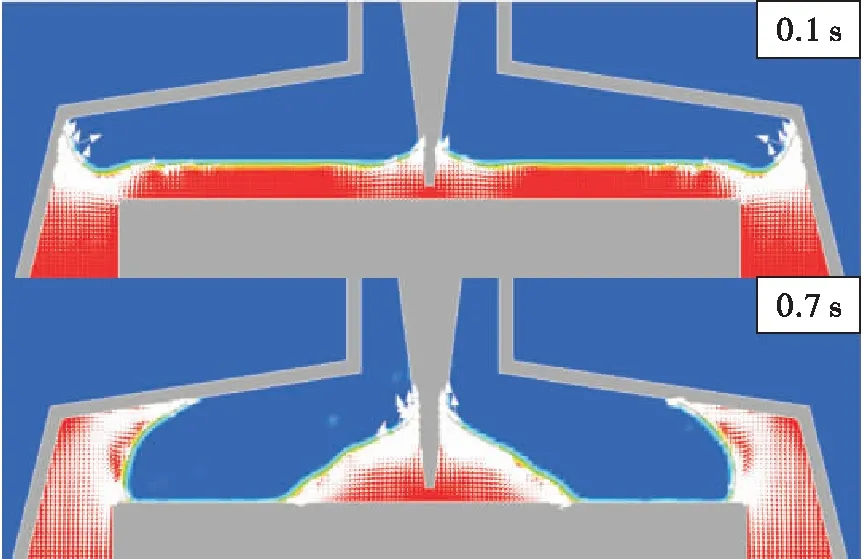
图18 速度矢量图Fig.18 Velocity vector illustration

最终，液体凸起分离为两部分，一部分留在篮内液池中，另一部分沿芯柱继续爬升。芯柱所抽吸的推进剂在表面张力的驱动下，爬升至排气管顶端。

对排气管内不设置芯柱的起动篮进行了对比分析，最终篮内气液界面的平衡状态如图19所示，排气管内没有推进剂。海绵结构能够将推进剂抑制在出液口位置，气体停留在上端，但是不能维持排气管顶端多孔毛细元件的湿润。

第二种工况的仿真结果表明篮内推进剂液面低于排气管时，芯柱可以有效实现推进剂导流以维持排气管顶端多孔毛细元件的湿润。

图19 气液界面平衡状态(无芯柱)Fig.19 Gas-liquid interface equilibrium state (without core)

3.3 引流片对导流效果的影响

为了进一步分析引流片数目对导流效果的影响，对第二种工况下6引流片芯柱的导流效果进行了数值仿真，结果如图20所示。

图20 4引流片(左)和6引流片(右)芯柱的导流效果Fig.20 Simulation results of the core with 4(left) and 6(right) deflector

仿真结果表明，4引流片和6引流片芯柱均在1.6 s时将推进剂导流至排气管顶端，且整个推进剂运动过程是相似的。在相关内角自流实验中，理论上两壁面夹角越小，对液体介质的导流速度越快。对于本文所设计的芯柱来说，4引流片芯柱已经实现了所需功能；另一方面，由于排气管内径较小，芯柱引流片数目过多，会增加加工制造的难度。实际工程应用中，需要针对具体任务要求，根据流动时间，确定芯柱引流片数目。

本文进行了柱形十字板芯柱结构推进剂导流效果研究。仿真结果发现，推进剂沿柱形十字板结构上升速度和效率非常低。对第一种工况使用柱形十字板结构进行的仿真，结果推进剂在6 s后仍未能达到排气管顶端，如图21所示。

柱形十字板结构将排气管内的推进剂分隔为4个封闭区域。而在每个区域中，推进剂沿十字板夹角的爬升速度反而低于其与壁面相交处的爬升速度。该现象是由于十字板板片外沿与排气管内壁面相交处内角小于十字板夹角90°而表面张力作用略强所导致的。各个区域中推进剂同时沿3个夹角爬升，所形成的气液界面近似处于平衡状态，难以保证内角自流的驱动压强。柱形十字板结构推进剂导流速率和效率均不高，故实际设计中未采用该结构方案。在实际设计中，排气管芯柱应避免形成相似的多夹角封闭区域。

4 结语

本文通过理论分析与数值模拟方法，针对可再充填起动篮存在的典型工况设计了排气管芯柱，并对其功能实现进行了仿真分析，为保持起动篮排气管顶端多孔毛细元件的润湿问题提出了解决方案，通过研究表明：

1)根据起动篮排气再充填和推进剂自保持工作原理，分析了排气管顶端多孔毛细元件润湿问题及其影响，并给出了芯柱结构作为该问题的解决方案；

2)从微重力流体力学和内角自流理论分析了芯柱对推进剂导流作用，具备理论上的可行性；

3)针对某起动篮表面张力贮箱两种典型工况，采用FLOW-3D软件进行仿真分析，验证了利用芯柱实现推进剂导流的方案正确性，可实现工程应用；

4)仿真分析了引流片数目对导流效果的影响和柱形十字板芯柱的导流效果，对优化芯柱结构设计提供了对比和借鉴。