烟羽应急计划区公众撤离模式研究
亓文辉,祁明亮
(1.中国科学院 科技战略咨询研究院,北京 100190; 2.中国科学院大学 公共政策与管理学院,北京 100049)
0 引言
截至2018年3月,中国大陆已建有17座核电站,38台在运核电机组[1]。我国以核反应堆(也称核岛)为中心,10公里为半径划定烟羽应急计划区,其中5公里范围为内区,5至10公里范围为外区[2]。一旦发生对应等级的核电站应急事故,烟羽应急计划区内的居民将按照一定的撤离程序,迅速撤离至指定安置点[3]。学界对于公众撤离采取何种方式,一直存在争议。在“政府组织撤离”模式中,政府组织大巴车,按照指定撤离路线,将公众运送到政府指定的临时安置点。当大巴车数量有限时,该撤离模式可能导致撤离群众长时间等待。随着机动车进入家庭,公众更倾向于选择私人交通工具自行撤离[4];然而,自行撤离的无序性会导致道路拥堵,影响大巴车的救援时间。从我国居民拥有交通工具的实际情况来看,“政府组织撤离”与“自行撤离”会同时出现在未来可能的公众疏散中。那么,在现有交通路网条件下,政府组织撤离和自行撤离的比例结构如何影响撤离时间,是否存在一个比例结构,使得撤离时间最短?
烟羽应急计划区公众撤离属于区域撤离问题。区域撤离的模式选择取决于灾害类型、可用交通工具种类、距离安全地点的路程等因素[5]。灾害发生时,超过80%的居民会利用私人交通工具自行撤离[4]。Benjaafa[6]与Chiu[7]分别从微观和宏观角度对自行撤离进行了研究。但是仍有部分居民需要依靠公共交通工具进行撤离[8],直到Katrina飓风之后,学者们才意识到公共交通撤离预案的重要性。在飓风期间,由于私人交通工具涌入道路,造成交通堵塞,导致撤离过程出现了不必要的延误[9]。之后,越来越多的学者开始致力于公共交通撤离模式的研究。Sayyady和Eksioglu[10]对洪水发生时的人员撤离进行研究,提出一种使用公共汽车进行居民撤离的模型,其目标为总撤离时间最短。但是该模型把初始行程分配作为输入,这种处理值得商榷。Dhingra和Roy[11]基于确定的公交车撤离路线建立了核电站场外疏散模型,该模型可用于确定车辆规模、志愿者和医务人员数量、资源分配方案,但未考虑不同路线对撤离时间的影响。此外,Goerigk等人利用分支定界算法[12]、两阶段鲁棒性方法[13]、具有信息延迟的鲁棒模型[14]对公共交通撤离模式下的相关问题进行研究。之后,Goerigk[15]等人又提出了公共汽车与私人交通工具混合的撤离模式,最大程度地减少撤离时间、撤离人员的暴露风险以及避难场所数量。Yang[16]等人考虑公共汽车、私人交通工具、地铁三种交通工具及其相互作用,撤离人员的合作行为和避难所的容纳能力,以最小化撤离时间为目标,建立了宏观多式联运网络应急撤离模型。但目前尚未检索到对公共与私人交通工具混合模式下烟羽应急计划区公众撤离问题进行研究的文献。
元胞传输模型是研究公众应急撤离的常用方法[17]。Chiu[7]等人基于元胞传输理论建立了无通知情况下大规模撤离的线性规划模型。Qi[18]考虑车辆往返运输的情况,以总撤离时间最短为目标建立了元胞传输模型。崔建勋[19]等人同样以系统疏散时间最短为目标,以元胞流量守恒和元胞容量限制等为约束条件,采用元胞传输理论建立了元胞-连接桥疏散路网模型。
总之,元胞传输模型可以捕捉到网络交通流中的不连续变化现象,清晰地描述系统中的排队现象,可以较好地模拟排队形成、排队消散以及路段间的相互影响等交通动力学特征,更真实地反映应急撤离的过程,更精确地计算应急撤离时间。为求解“政府组织撤离+政府指导下的自行撤离”模式下居民的最短撤离时间,本文考虑撤离路网结构、村庄位置以及车辆数量等限制,以最小化撤离时间为目标,建立基于元胞传输理论的公众撤离模型;通过调节私家车运送居民的比例,求解大巴车与私家车不同比例结构下的最短撤离时间,探索政府组织撤离与居民自行撤离的比例结构对撤离时间的影响。
1 问题描述
针对烟羽应急计划区公众应急撤离问题,考虑大巴车与私家车两种撤离工具进行撤离。“政府组织撤离”中,大巴车从车站出发,前往村庄运输居民,之后驶往大巴车安置点,到达大巴车安置点即为完成撤离;必要时大巴车可多次前往村庄运输居民,但每一次运输过程中,大巴车只到达一个村庄。“政府指导下的自行撤离”模式采用的撤离工具为私家车,私家车从村庄出发,到达烟羽应急计划区外区边界处即可视为完成撤离,并且私家车只进行一次运输。基本假设如下:
(1)撤离居民能够遵循撤离通知进行撤离;
(2)撤离过程中无交通事故发生;
(3)撤离过程中涉及的私家车和大巴车均参与撤离;
(4)大巴车收到应急通知后立即从车站出发;
(5)需要乘坐大巴车撤离的居民在大巴车到达之前已在集结地点等待。
已知车站的大巴车数量和每个村庄的私家车数量,大巴车与私家车的额定载客量,大巴车安置点的位置、数量及容量;烟羽应急计划区的村庄位置及数量、每个村庄的居民总数。在撤离过程中考虑烟羽应急计划区的路网结构、道路长度、道路的自由流速度、道路的堵塞密度和道路通行能力。在“政府组织撤离+政府指导下的自行撤离”模式下,求解前往不同村庄的大巴车数量、大巴车与私家车的撤离路线,从而使撤离时间最短。
为了研究在不同的大巴车与私家车比例结构下居民最短撤离时间的变化,本文使私家车运送居民的比例在0%~100%之间变化,每次变化幅度为10%,且每个村庄的私家车均按照相同比例运送居民。
2 基于元胞传输理论的公众撤离模型
参数说明:
C:所有元胞集合;
Cs⊂C:首元胞集合;
Ce⊂C:尾元胞集合;
Cj⊂C:集结地点与大巴车安置点元胞集合;
Ct⊂C:交叉路口元胞集合;
Cc⊂Ct:相互冲突的元胞连接桥所连接的元胞集合;

Γi:i元胞的下游元胞集合;
T:离散时间集合;
t∈T:离散时间;
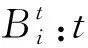
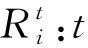

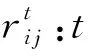

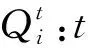
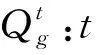
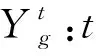
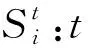
Mi:集结地点元胞i中需要的大巴车数或大巴车安置点元胞i中需返回村庄的大巴车数;
ai:i元胞内车辆的自由流速度;
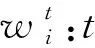

决策变量:


模型建立:
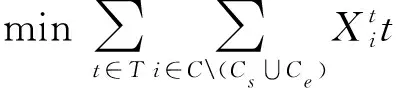
(1)

(15)
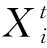
3 案例分析
3.1 D烟羽应急计划区案例
3.1.1 基本信息
D烟羽应急计划区内区共有6个行政村,总人数为7691人,私家车保有量为379辆,每辆私家车限坐5人,具体人口与私家车分布情况如表1所示;D市汽车站共有45座大巴车138辆,根据现有撤离预案设置1个大巴车安置点。

表1 D烟羽应急计划区内区人口与私家车分布表
大巴车从D市汽车站出发,经由省路、国道、县路、村路到达相应村庄;然后又前往大巴车安置点,大巴车行驶路线仅在将要到达村庄时有所差异。私家车撤离时,只要撤离到烟羽应急计划区外区边界处即为完成撤离,因此将D烟羽应急计划区范围内主要路网绘制如图1所示。图1中两个圆形分别表示D烟羽应急计划区内区(5km)和外区(10km)的边界,加粗实线线条表示国道,点划线线条表示城市道路,实线线条表示县路,虚线线条表示村路。
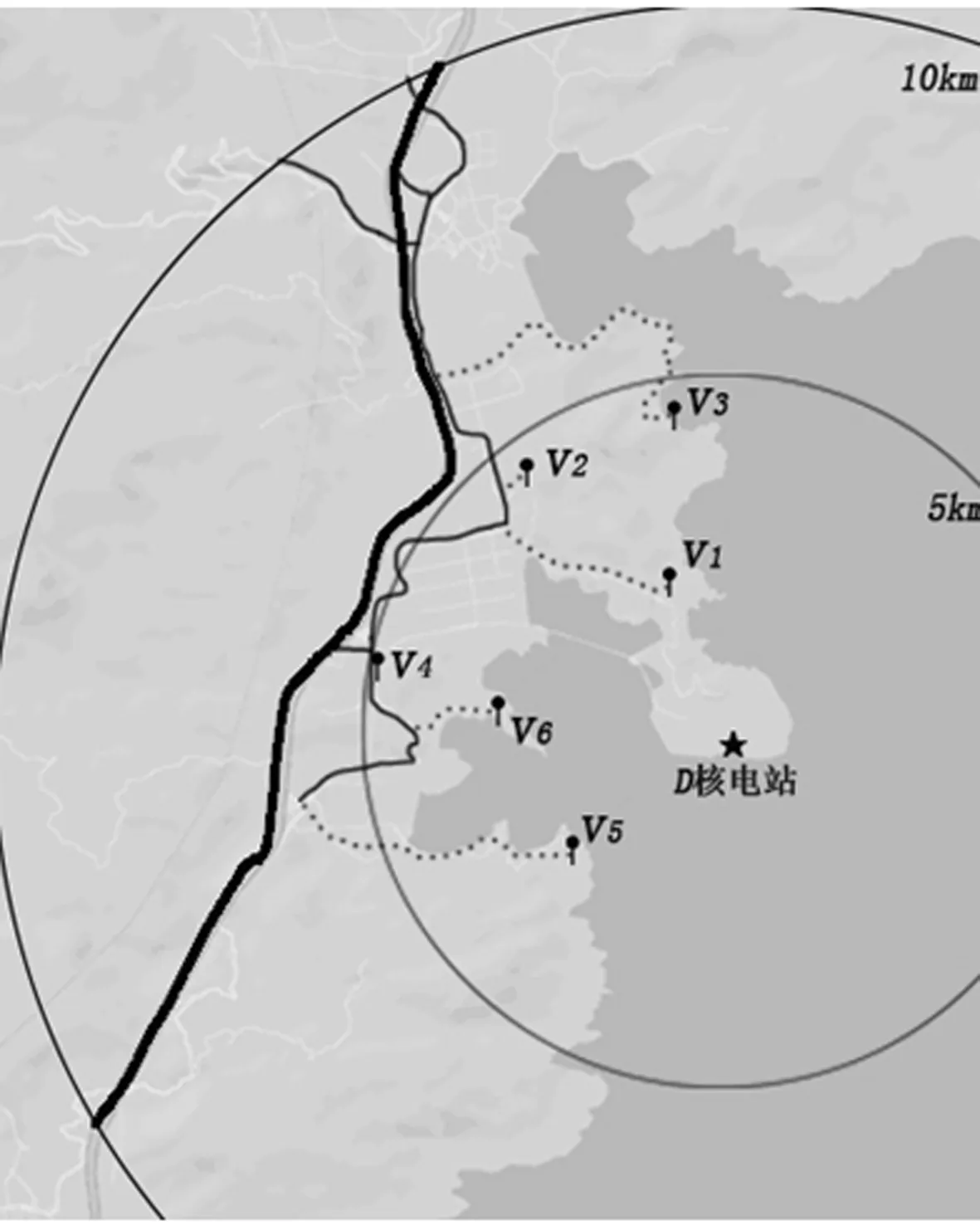
图1 D烟羽应急计划区主要路网图
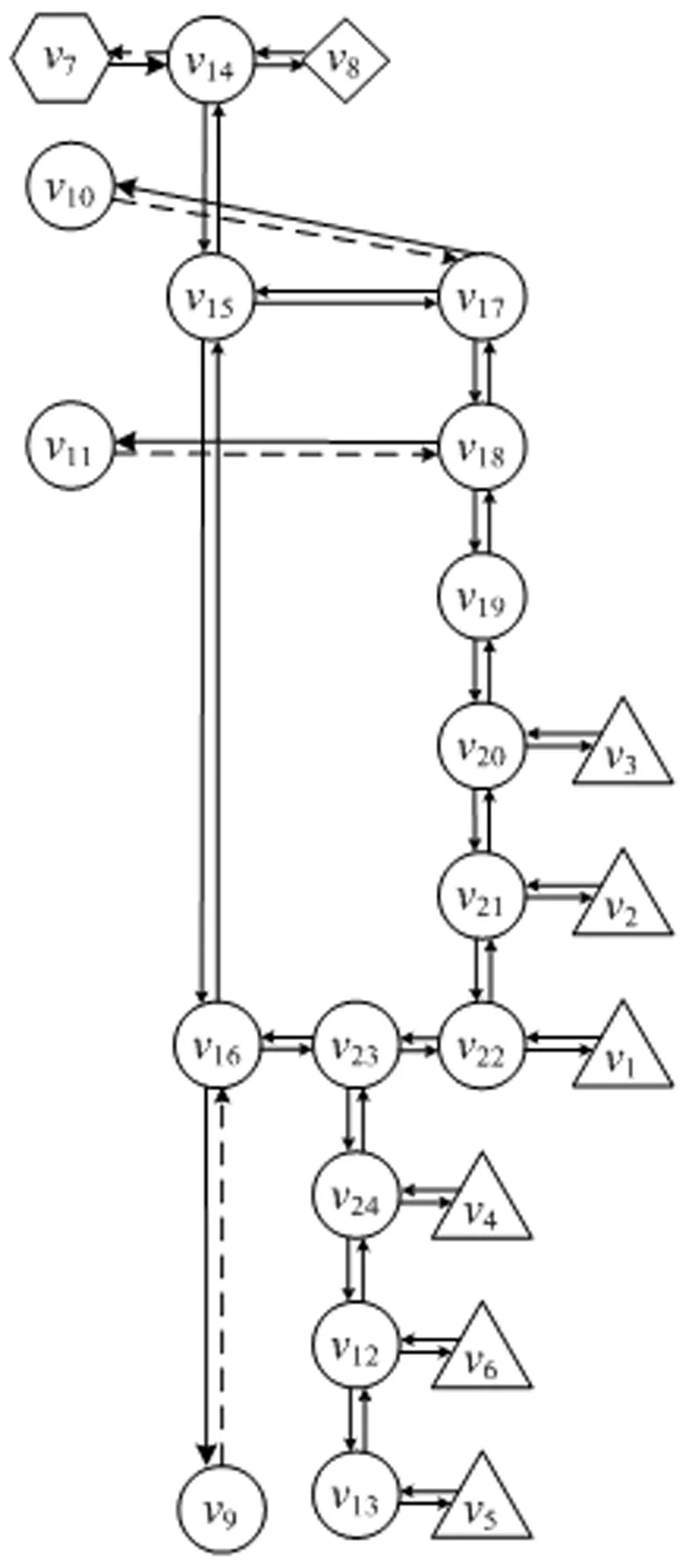
图2 D烟羽应急计划区内区撤离路网图
将路线进行整理,得到D烟羽应急计划区内区居民的撤离路网如图2所示。图中vi,i=1,2,3,…,24表示路网中的节点,ei,j,i≠j表示节点vi到节点vj的路段,六边形代表大巴车车站,三角形代表村庄,圆形代表交叉路口,菱形代表大巴车安置点。
根据撤离流程,路网中的e14,7、e10,17、e11,18与e9,16路段没有得到利用,这四条路段在图2中以点划线进行标注。本文采取反流策略[21],改变这四条路段中车辆的行驶方向,即路段e7,14、e17,10、e18,11与e16,9的车道数加倍。
私家车的出发时间服从参数为20min的泊松分布,需要乘坐大巴车撤离的居民上车与下车时间均为8min。一般取堵塞密度为133pcu/km,一辆当量小轿车占据的道路长度为7.5m,每个时间段t的长度为2min,元胞长度=该路段自由流速度×时间段长度[19],单路段元胞数量=路段长度÷元胞长度,元胞容量=元胞长度÷一辆当量小轿车占据的道路长度×该路段的车道数。反向传播速度可由式(16)得到。查看《城市道路工程设计规范》(CJJ37-2012)[22]可了解到不同速度下的道路通行能力,并根据道路宽度进行调整[23],得到单位时间的允许通过的最大流量。表2描述了路网的几何参数与元胞特性。
(16)
式中,ρjam、qmax、a和w表示堵塞密度、最大交通流量、自由流速度和反向传播速度。
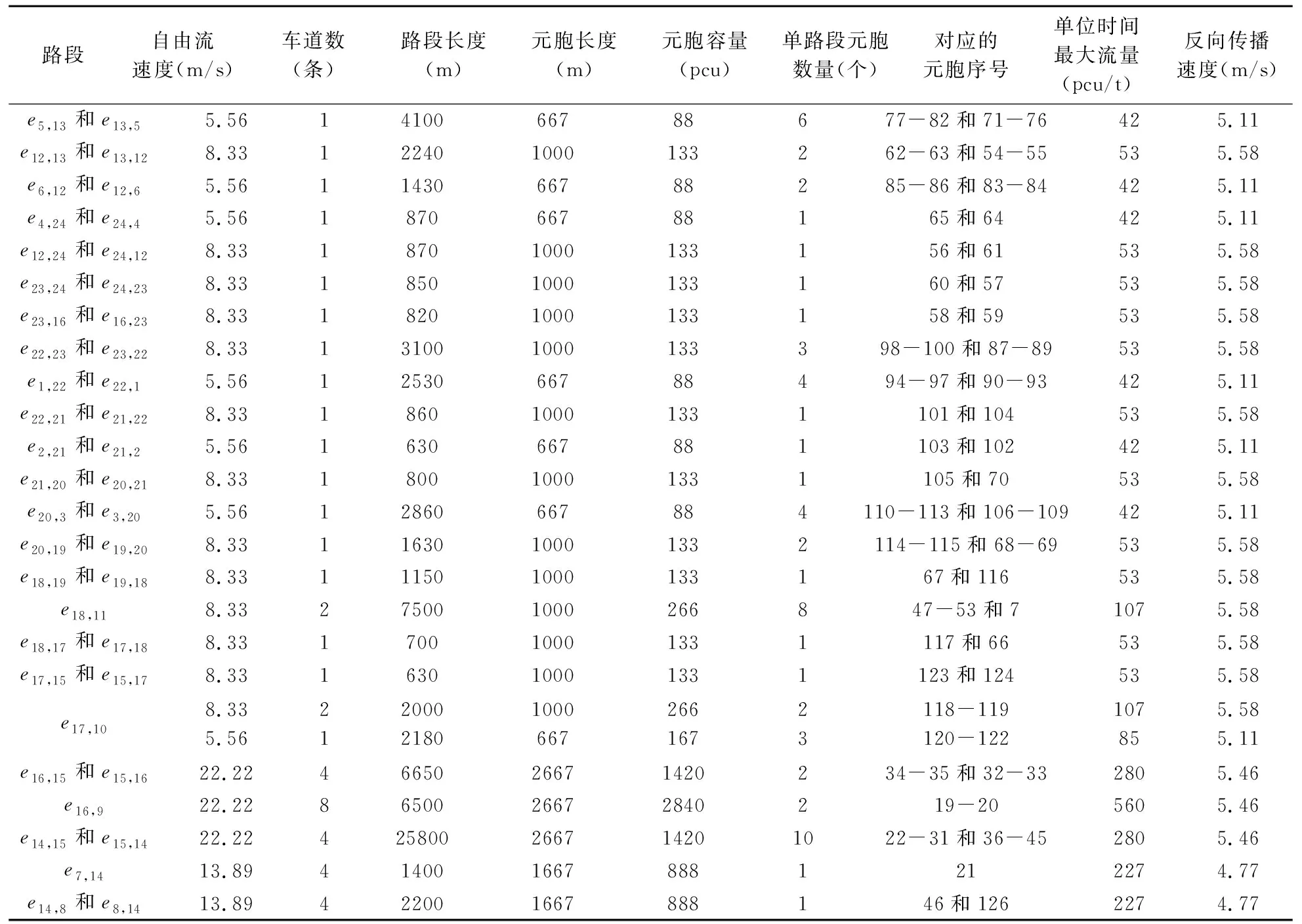
表2 D烟羽应急计划区内区撤离路网的几何参数与元胞特性
根据表2中路网的几何参数及元胞特性,绘制D烟羽应急计划区内区居民撤离路网的元胞结构图如图3所示。图中将烟羽应急计划区外区边界处的元胞设置为私家车撤离的终点,即尾元胞。整个路网共划分为127个元胞,包括7个首元胞和5个尾元胞,首元胞和尾元胞的容量均为无穷大。1~6元胞分别表示村庄v1~v6,7元胞表示大巴车站,8元胞为大巴车运行的终点,9、10、11与127元胞为私家车运行的终点,13~18元胞为集结地点元胞。私家车数量较少时,大巴车需要在125元胞放下所载居民,再次前往村庄。
3.1.2 模型求解与验证
当村庄中所有私家车均用于运送居民时,仍有部分居民需要乘坐大巴车撤离,利用Lingo软件求解得到大巴车与私家车的撤离路线如表3所示,此时撤离时间为114分钟。

表3 D烟羽应急计划区内区撤离路线表
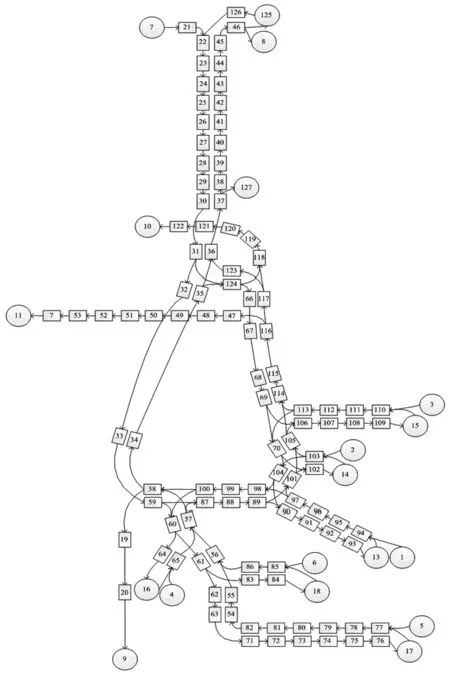
图3 D烟羽应急计划区内区撤离路网元胞结构图
为验证撤离模型的正确性,本文选用Anylogic仿真软件[24]对上述参数进行建模。Anylogic仿真模型的撤离时间为114分,与本节中公众撤离模型的结果一致,证明了公众撤离模型具有有效性与可行性。但Anylogic软件必须输入给定的撤离方案,方能估计撤离时间,不用于撤离路线的优化。
3.1.3 计算结果
日常情况下,核应急撤离所用大巴车处于正常营运状态;若增加大巴车数量,将会增加政府的营运成本。而私家车保有量的增加是经济发展的必然结果,因此本文重点研究私家车数量变化对撤离时间的影响。令私家车运送居民的比例在0%~100%之间变化,每次变化幅度为10%,且每个村庄的私家车均按照相同比例运送居民,通过公众撤离模型求解得到撤离时间随私家车运送居民数变化的折线如图4所示。
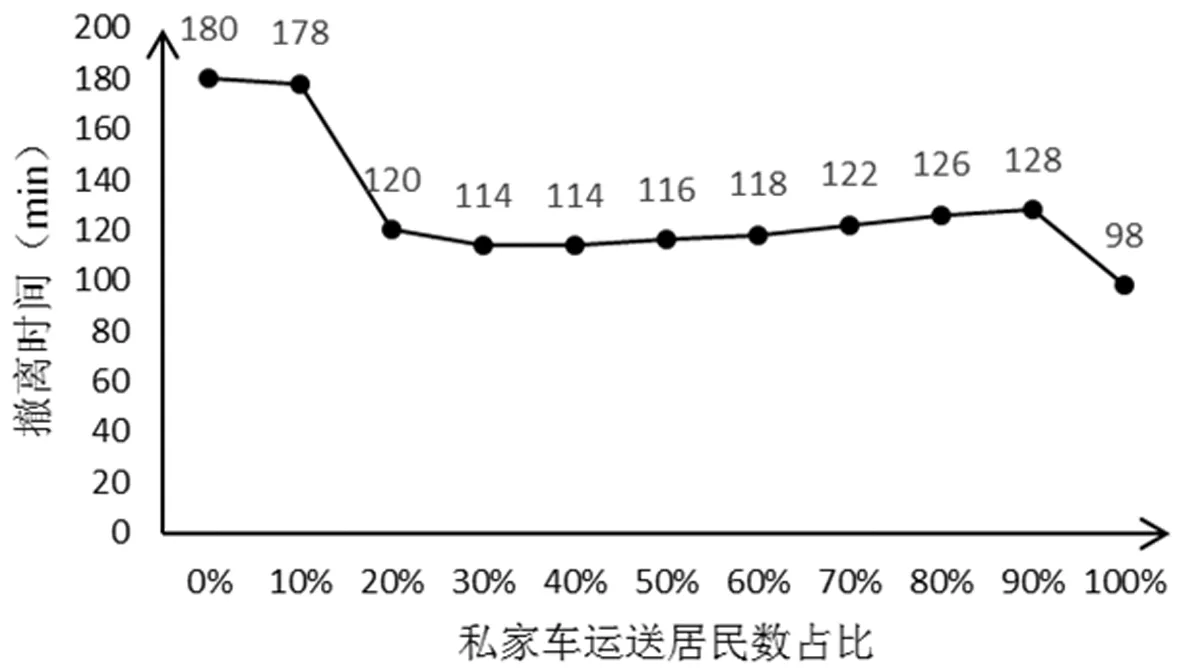
图4 D烟羽应急计划区内区居民撤离时间变化图
私家车运送居民的比例为0%~90%时,撤离时间为最后一辆大巴车到达大巴车安置点的时间。私家车运送居民的比例为0%、10%时,分别有35、19辆大巴车进行二次运输,导致撤离时间较长。私家车运送居民比例不低于20%时,大巴车只需一次运输即可完成所有居民的撤离;受到道路容量与道路交通能力的限制,在驶离高速公路时,道路由4车道变为2车道,车辆最高行驶由80km/h变为30km/h。私家车运送居民比例为20%时,大巴车在驶离高速公路的31与33元胞处出现交通堵塞,堵塞时间均为4min。私家车运送居民比例为30%、40%时,没有明显的堵塞现象发生。私家车运送居民比例为50%时,私家车数量增加到770辆,其中v5村庄私家车数量为243辆。v5村庄的私家车从55元胞行驶至56元胞时,前往v6村庄的大巴车从61元胞行驶至83元胞,大巴车与私家车在该路口出现了拥堵,拥堵时间为2min。前往v5村庄的大巴车在17元胞满载居民时,与从5元胞驶出的私家车产生冲突;由于77元胞道路容量的限制,大巴车驶离17元胞的时间出现了4min的延迟。在其他交叉路口,由于大巴车与私家车的运行在时间与空间上不完全冲突,因此未产生交通拥堵现象,影响车辆运行时间。私家车运送居民比例为60%~90%时,随着私家车数量的增加,在55、61与17元胞处均发生不同程度的交通堵塞,影响大巴车的行驶时间,使撤离时间逐渐增加,但不超过完全依靠大巴车进行撤离时的撤离时间。私家车运送居民比例为100%时,所有居民均依靠私家车运送,撤离时间为最后一辆私家车撤离至D烟羽应急计划区外区边界处的时间。
随着私家车运送居民比例的增加,撤离时间出现先减少,后增加,再减少的趋势。由于大巴车需从车站前往村庄,再撤离到指定的大巴车安置点,行驶路程长;私家车只需撤离到烟羽应急计划区外区边界处,行驶路程短,因此全部居民均由私家车运送时,撤离时间最短。但完全依靠私家车撤离的模式要求每5个人即拥有一辆私家车,对经济发展水平要求过高,在很长一段发展时间内无法实现。因此选取私家车运送居民比例30%、40%为最佳比例,撤离时间为114min,此时的撤离路线与表3中的撤离路线完全相同。
目前D烟羽应急计划区内区各村庄的私家车保有量为379辆,撤离时间为114min。在“政府组织撤离+政府指导下的自行撤离”模式下,应该令使所有私家车参与到撤离活动中,从而实现最快速的撤离。
3.2 Q烟羽应急计划区案例
3.2.1 基本信息
Q烟羽应急计划区内区共有6个行政村,共15562人,具体分布如图7所示, 私家车保有量为767辆,每辆私家车限坐5人,具体人口与私家车分布情况如表4所示;撤离所需大巴车来自于Q市汽车站,该站共有45座大巴车170辆,根据现有撤离预案设置1个大巴车安置点。

表4 Q烟羽应急计划区内区人口与私家车分布表
根据百度地图显示路网,绘制撤离所涉及的所有路段如图5所示,并将路线进行整理,得到图6所示路网图。
每个时间段t的长度为4min,其他参数选取与D烟羽应急计划区内区居民撤离路网的参数相同,得到Q烟羽应急计划区内区居民撤离路网的元胞参数如表5所示,并具此绘制路网的元胞结构图如图7所示。图7中将烟羽应急计划区外区边界处的元胞设置为私家车运行的尾元胞,整个路网共划分为109个元胞,包括7个首元胞和5个尾元胞,首元胞和尾元胞的容量均为无穷大。1~6元胞分别表示村庄v1~v6,7元胞表示大巴车站,8元胞为大巴车运行的终点,15~18元胞为私家车运行的终点,9~14元胞为集结地点元胞。私家车数量较少时,大巴车需要在19元胞放下所载居民,再次前往村庄。

图5 Q烟羽应急计划区主要路网图

图6 Q烟羽应急计划区内区撤离路网图
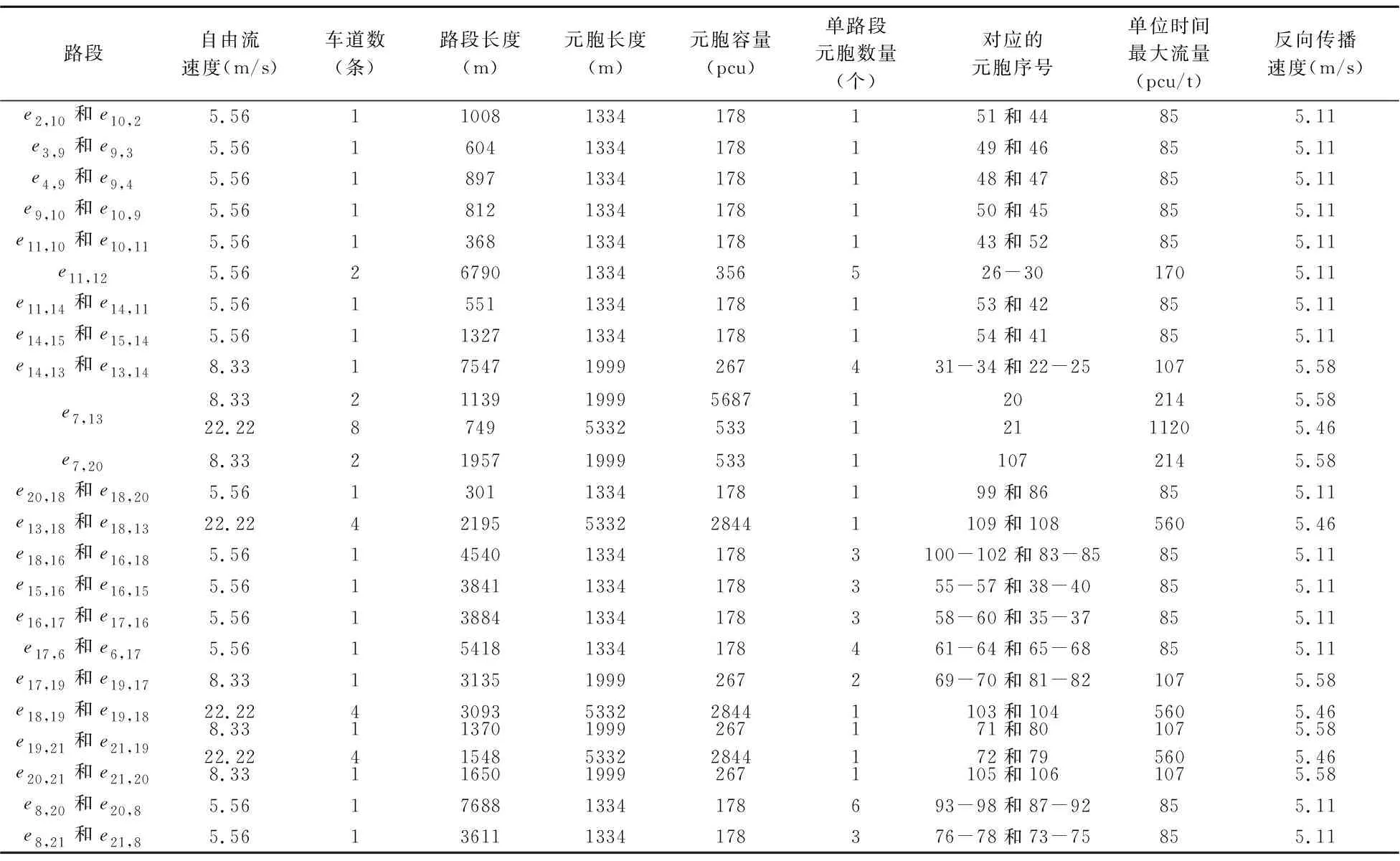
表5 Q烟羽应急计划区内区居民撤离路网的几何参数与元胞特性
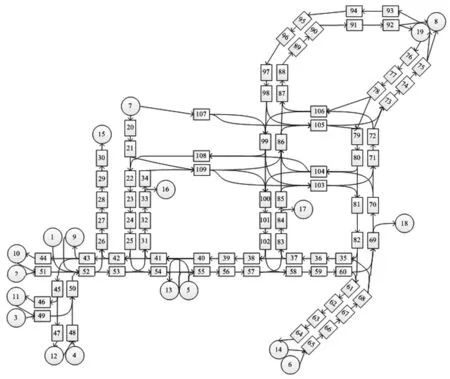
图7 Q烟羽应急计划区内区撤离路网元胞结构图
3.2.2 计算结果
令私家车运送居民的比例在0%~100%之间变化,每次变化幅度为10%,且每个村庄的私家车均按照相同比例运送居民,得到撤离时间随私家车运送居民数量变化的折线如图8所示。

图8 Q烟羽应急计划区内区居民撤离时间变化图
私家车运送居民的比例为0%~90%时,撤离时间为最后一辆大巴车到达大巴车安置点的时间。私家车运送居民的比例为0%时,居民完全依靠大巴车进行撤离,在所有大巴车均进行二次运输的基础上,仍有8辆大巴车需要进行三次运输,才能完成所有居民的撤离。私家车运送居民比例为10%~50%时,需要进行二次运输的大巴车数量分别为:145、109、74、41、5。私家车运送居民比例为60%时,大巴车仅需一次运输即可完成所有居民的撤离,但此时撤离需要的私家车数已经多达1867辆,对大巴车的行驶产生了影响。自v1村庄驶出的私家车从1元胞驶向52元胞,与从43元胞驶向44、45元胞的大巴车均产生冲突;自v2村庄驶出的私家车从51元胞驶向52元胞,与从43元胞驶向45元胞的大巴车产生冲突;自v3村庄驶出的私家车从49元胞驶向50元胞,与从45元胞驶向47元胞的大巴车产生冲突,在43、45、49、51元胞处造成12min、4min、8min、4min堵塞。私家车运送居民比例为70%~90%时,在43、45、49与51元胞处的堵塞现象更加严重,使得大巴车到达大巴车安置点的时间逐渐增加,但不超过完全依靠大巴车进行撤离时的撤离时间。私家车运送居民比例为100%时,所有居民均依靠私家车运输,撤离时间为最后一辆私家车撤离至Q烟羽应急计划区外区边界处的时间。
完全依靠私家车进行撤离时,Q烟羽应急计划区内区的私家车数量远远多于D烟羽应急计划区内区的私家车数量,在道路上发生了严重的堵塞,此时撤离时间并不是最短撤离时间。撤离时间最短时,私家车运送居民比例为60%,最短撤离时间为160min,此时的撤离路线如表6所示。
目前Q烟羽应急计划区内区各村庄的私家车保有量为767辆,仅能运送25%的居民,处于最佳比例的左侧。随着经济的发展,在Q烟羽应急计划区内区各村庄的私家车保有量增加至4669辆(可运送60%的居民)之前,应使所有私家车参与到核应急撤离中。
3.3 结果讨论
据图6与图11显示,撤离时间随私家车数量的增多呈现先减少,后增加,再减少的趋势。“政府组织撤离+政府指导下的自行撤离”模式下撤离时间均小于“政府组织撤离”模式时的撤离时间。“政府组织撤离+政府指导下的自行撤离”模式时,政府组织撤离与居民自行撤离之间均存在一个最佳比例结构,使居民撤离时间达到相对小。
由于路网结构与居民分布情况的原因,D烟羽应急计划区内区居民自行撤离时间为所有情况下的最短撤离时间;而Q烟羽应急计划区内区居民自行撤离时间并非最短。D烟羽应急计划区内区居民撤离路网主要包括国道、县路和村路,而Q烟羽应急计划区内区居民撤离路网以县路和村路为主,道路的车道数少,道路允许的车辆行驶速度慢。因此,私家车运送相同比例居民时,Q烟羽应急计划区内区居民撤离时间长于D烟羽应急计划区内区居民的撤离时间。
D与Q烟羽应急计划区内区撤离车辆拥堵情况均发生在大巴车与私家车交汇的路口。在Q区内的43、45、49、51元胞处,D区内的55、61元胞处,均出现了进入救援的大巴车与驶出的私家车车流冲突,增加了居民撤离时间。建议在Q烟羽应急计划区内区的1、2、3、4村庄附近增建道路;在D区内区5村庄增建驶往D电站反方向的道路,避免车流冲突。
此外,D烟羽应急计划区内区村庄5的人口多,距离高速公路远,村庄附近道路设计通行低。建议拓宽5村庄附近的道路宽度,方便大巴车与私家车驶离村庄;Q烟羽应急计划区内区1、2、3、4村庄人口较多且位置相对集中,私家车驶离村庄时,易发生拥堵。建议当地政府拓宽村庄附近道路或增建驶往Q电站反方向的道路。
4 结论
本文基于元胞传输理论建立了烟羽应急计划区公众撤离模型,采用lingo软件和Anylogic软件分别进行模型求解与验证。考虑大巴车与私家车的不同比例结构,对不同情况下的居民撤离时间进行研究。通过案例分析,得到以下结论:(1)政府组织撤离与自行撤离之间存在一个最佳的比例结构,使撤离时间达到相对低的水平;(2)公众完全自行撤离的时间不一定是最短的;(3)在文章假设条件下,“政府组织撤离+政府指导下的自行撤离”模式的撤离时间可能小于“政府组织撤离”模式的撤离时间。建议当地主管部门动态跟踪当地居民拥有交通工具情况,当私人交通工具可运送居民的比例小于最佳比例时,重点引导居民撤离路线和行为;当私人交通工具可运送居民的比例大于最佳比例时,应采取一定措施,例如培训演习等方法,使参与撤离的私人交通工具运送居民比例为最佳比例。
未来研究中,将增加风向作为影响道路是否可以通行的因素,即处于下风向的道路不作为撤离路线,以减小受污染的风险。

