基于初始值和背景值改进的GM(1,1)模型优化与应用
卢 捷,李 峰
(江南大学 商学院,江苏 无锡 214122)
0 引言
灰色预测是灰色系统理论的主要内容之一,GM(1,1)模型作为灰色预测理论的核心和基础[1],在很多领域都得到了广泛的应用。然而在实际应用中,经典GM(1,1)模型会出现预测精度不稳定、甚至出现偏差的情况[2]。由于经典GM(1,1)模型误差来源主要集中于初始值的选取以及背景值的构造,为此学者们从不同角度对GM(1,1)模型的改进进行了研究,并在初始值、背景值方面取得了一定的成果。
在初始值优化方面,考虑到新信息在建模中应当发挥关键作用,罗佑新[3]直接以x(0)(n)作为灰色模型初始条件,虽然可以在一定程度上减少误差,但缺乏严格的理论依据;党耀国[4]分别以x(1)(n)作为灰色模型初始条件,弥补了以往学者研究的缺陷,但同样没有严格的理论证明;Wang等针对白化方程为非齐次指数函数对模型初始值进行优化,进而构造新的背景值表达式减少模型误差,提高模型预测精度[5],优化方法适用范围较窄。
在对背景值优化方面,经典模型对于背景值z(1)(k)的构造并没有严格的理论依据,故学者们从不同角度对背景值进行改进,大致可分为从几何意义以及数列特征两个方面进行优化。从积分的几何意义出发,蒋诗泉等[6]利用分段低次插值,结合复化梯形公式计算各区间积分之和,以减少因在[k-1,1]区间直接计算整个梯形面积造成的误差;而江艺羡[7]则利用黎曼积分,以不规则梯形面积取代传统梯形面积构造法,对传统GM(1,1)模型背景值进行优化。从序列数值特点出发,彭振斌等[8]将数据序列抽象为非齐次指数函数构造背景值,构建GM(1,1)模型;Cai[9]则在原始序列间距不一致情况下对背景值进行改进,以扩展经典模型的适用性和精确性。此外,也有学者基于不同角度提出了z(1)(k)的数学表达式[10~12],也在一定程度上提高了预测精度。而在模型参数估计方面,孟伟等[13]采用粒子群优化算法,Lee等[14]采用遗传算法等对经典模型进行优化都取得了较好的预测效果。
可以看出,在对背景值优化方面,现有研究主要是对紧邻均值构造方法进行改进,且均提出了一定的改进方法,但大部分学者都是对模型某一方面的优化,虽然可以在一定程度上提高精度,但不能系统地减少模型误差;同时在初始值选取方面,由最小二乘法原理可知,拟合曲线并不一定通过点(1,x(1)(1))。虽然有部分学者提出改进方法分别以x(1)(n)为固定点,但在模型涉及多变量的情况下,这种方法的效果还有待检验。
1 经典GM(1,1)模型误差分析
根据GM(1,1)模型基本形式x(0)(k)+az(1)(k)=b的白化方程,即
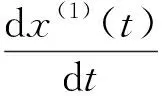
(1)
对式(1)在[k-1,k]上求积分可得
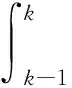
(2)
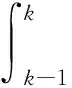
(3)
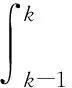
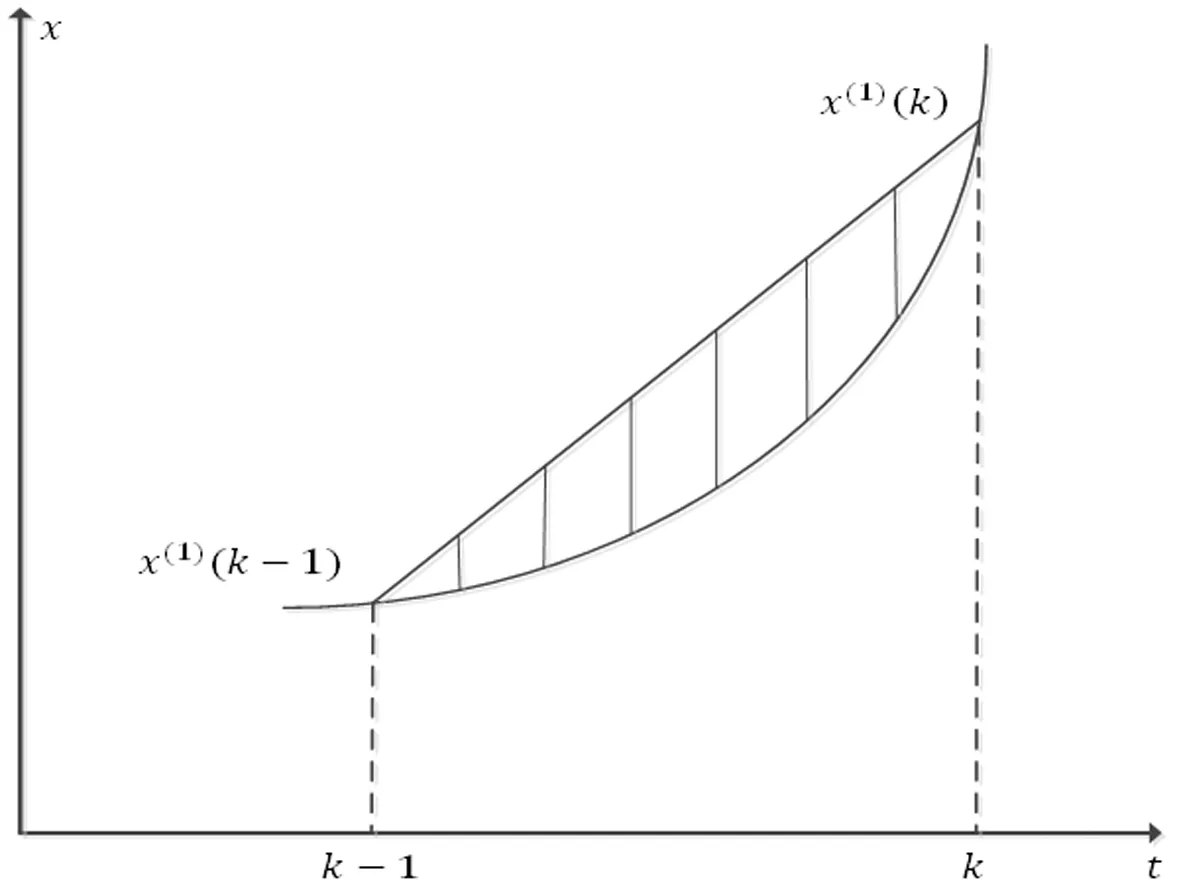
图1 GM(1,1)模型背景值误差来源
经典模型对背景值的计算公式为
z(1)(k)=0.5(x(1)(k)+x(1)(k-1)),k=2,3,…,n
当一次累加生成序列变化较为平缓,且当时间间隔较小时,采取以上方法计算是合适的;但当一阶累加生成序列波动较大时,采取以上方法则会造成较大的误差。从数列生成特征来看,经典模型人为地规定旧信息和新信息同等重要,这并不符合实际。本文将背景值视为变量,即z(1)(k)=(αz(1)(k)+(1-α)z(1)(k-1)),由MRE取到最小值时再确定背景值参数值以及时间响应式具体形式,可以显著降低人为因素造成的误差,提高预测精度。
同时,在对背景值进行优化的基础上,也对初始值进行优化。灰色GM(1,1)模型作为指数预测模型,本质是以x(1)(1)为固定点的静态方程。相较于动态方程,静态方程并不具有基准选值无关性,步长无关性,内在一致性等特征,拟合效果通常要比动态方程更差一些,应用范围也没有动态方程广阔[15]。利用一阶线性差分方程,用一个变动的已知时刻去预测将来的未知时刻的值,对传统数值解法进行改进,可提高拟合精度。
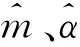
2 灰色GM(1,1)模型的改进
2.1传统GM(1,1)模型
定义1[16]设非负原始序列
X(0)=(x(0)(1),x(0)(2),…,x(0)(n))
称X(1)为X(0)的一次累加生成(1-AGO)序列:
X(1)=(x(1)(1),x(1)(2),…,x(1)(n))
GM(1,1)模型的原始形式为
x(0)(k)+ax(1)(k)=b
(4)
定义2[17]X(0),X(1)如定义1所示,令
Z(1)=(z(1)(2),z(1)(3),…,z(1)(n))
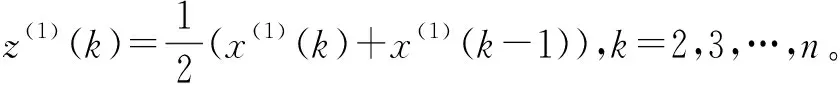
则GM(1,1)模型的基本形式为
x(0)(k)+az(1)(k)=b
(5)
其白化方程为

(6)
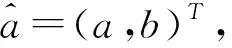
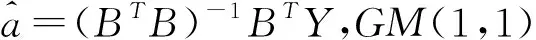
(7)
其还原值为
(8)
(9)
其中k=2,3,…,n。
从(9)式可以看出,GM(1,1)模型的预测精度取决于固定点的选取和参数a,b的值,而a,b的值又取决于背景值的构造。将初始值和背景值进行组合优化可显著提高模型精度。
2.2 灰色GM(1,1)模型的改进
2.2.1 初步改进方法(1)
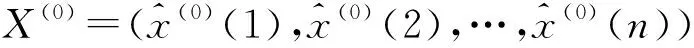
GM(1,1)模型的基本形式为x0(k)+az(1)(k)=b,其中,
z(1)(k)=0.5(x(1)(k)+x(1)(k-1)),k=2,3,…,n
(10)
带入(8)式可得:
(11)
则a,b可以由下式估计得到:
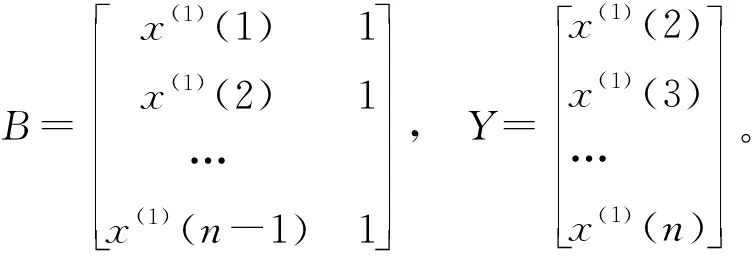
将a,b计算结果带入(7)式,并根据(5)和(6)式得到拟合序列。
2.2.2 初步改进方法(2)
在方法(1)基础上对模型的背景值进行改进,使平均相对误差取到最小值。其他条件不变,将(10)式改写为
z(1)(k)=(αx(1)(k)+(1-α)x(1)(k-1)),k=2,3,…,n
权重α满足0≤α≤1。由x(0)(k)=x(1)(k)-x(1)(k-1),k=2,3,…,n可得:
(x(1)(k)-x(1)(k-1))+(αx(1)(k)+(1-α)x(1)(k-1))=b
其一阶线性差分方程形式为:
(12)
则a,b可以由下式估计得到:
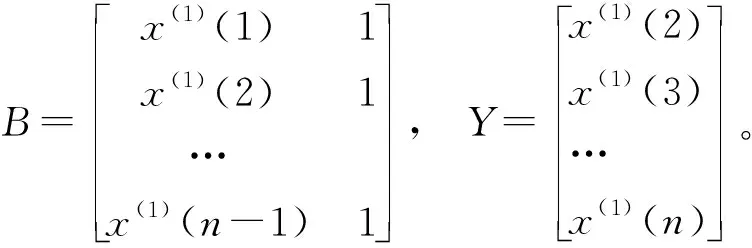
设上式计算结果为(c1,c2)T,解方程组可得:
a=(c1-1)/(α-αc1-1)
(13)
b=(-c2)/(α-αc1-1)
(14)
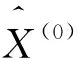
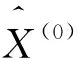
2.2.3 综合改进方法(3)
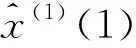
x(1)(k+1)=(x(1)(m)-b/a)e-a(k-m+1)+b/a
其中,m可依次选用m=1,2,…,n。将(13)和(14)带入下式
(15)
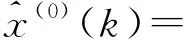
(16)
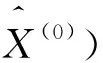
带入(16)式可得
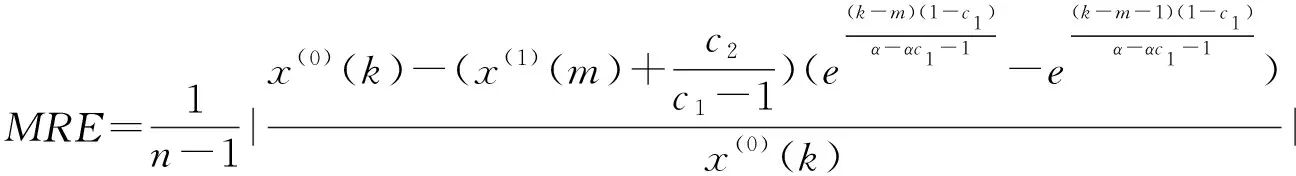
3 算例
我国目前是世界第一大石油进口和消费国。由于我国目前处于工业化阶段的中后期,能耗较大的汽车、家电等产品在经济中比重较高;同时,随着我国经济水平的快速发展,国内对于石油需求大幅提升,石油消费持续较快增长。然而,我国国内石油产量当前还满足不了巨大需求,使得在面临国内外市场供需失衡、市场供给不足时,难以短时间内保障油品供应,不断增长的需求只能通过加大进口来弥补。石油作为我国重要的能源,不仅为生活和生产提供强力的支撑,也关系到社会的安全与稳定。对我国石油年消费量进行预测,不仅有利于维持国内石油供需平衡,也可以为国家重大政策的制定提供依据。
从国家统计局网站获取2006~2017年中国国内石油年消费量,以2006~2015年数据为定参序列数据,2016~2017年数据为模拟序列预测对比数据,即
X(0)=(322,346,364,388,438,453,476,488,518,543)
2016~2017年数据分别为578,590(单位:百万吨)。
首先用未加改进的GM(1,1)模型进行计算。对原始序列进行一阶累加,可得
X(1)=(322,668,1032,1420,1858,
2311,2787,3275,3793,4336)
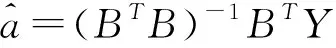
根据(8)式可得拟合序列并计算MRE。
应用初步改进方法(1)进行计算,将原始数据带入可得
根据(8)式可得拟合序列并计算MRE。拟合数据和预测数据见表1。
将原始数据带入方法(2)中,
可得
a=0.0537/(α-1.0537α-1)
(17)
b=-340.6913(α-1.0537α-1)
(18)
不妨可先设α=0,然后令其在区间[0,1]变化且Δα=0.01,利用matlab可得到MRE随α变化图2。
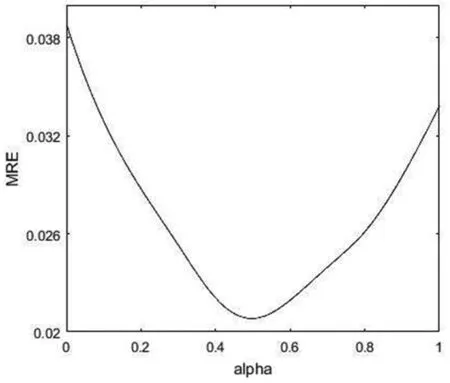
图2 方法(2)条件下MRE随α变化图
根据(8)式可得拟合序列并计算MRE。经典模型、改进方法(1)和方法(2)拟合数据和预测数据见表1。
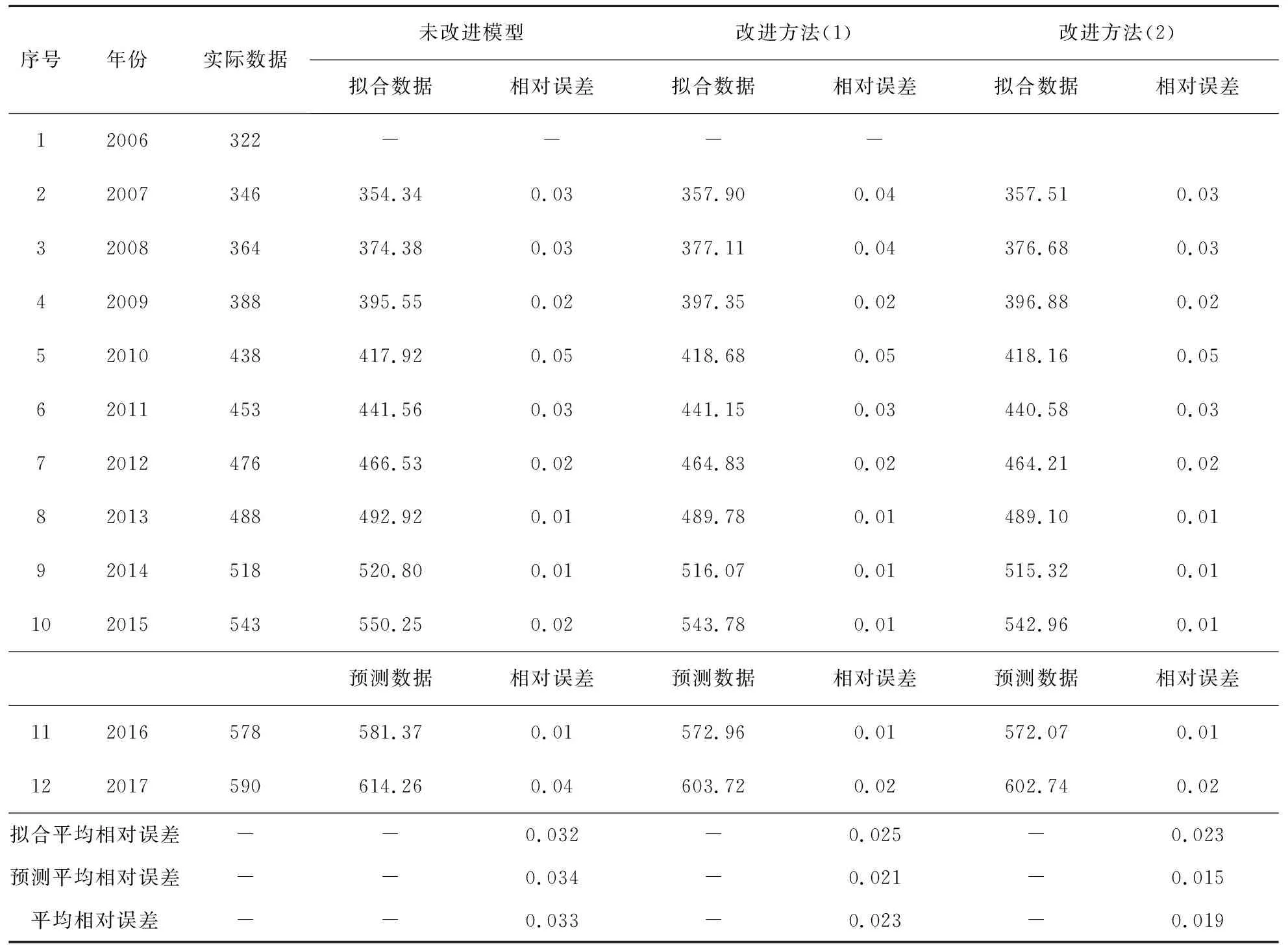
表1 中国国内石油年消费量预测(百万吨)
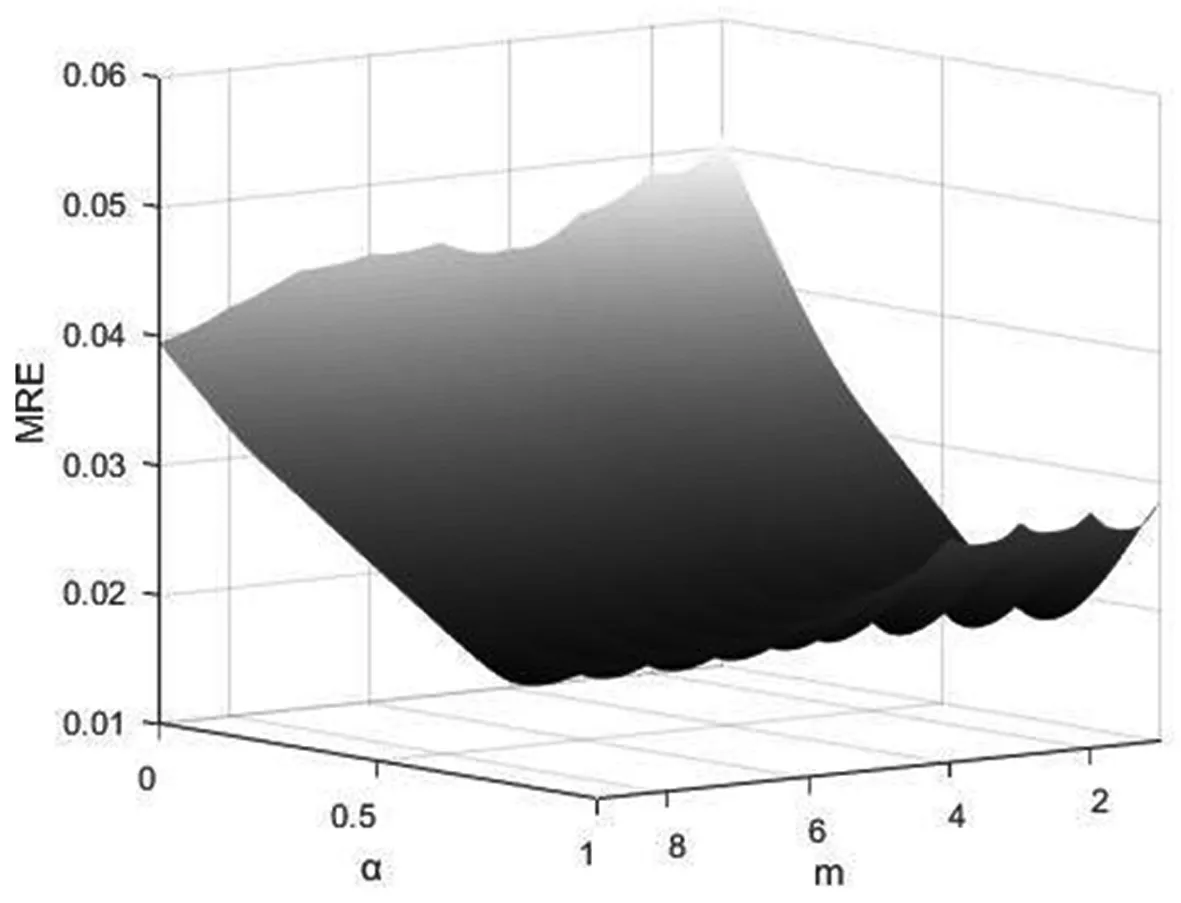
图3 MRE随m和α变化图
在计算方法(2)的基础上,将原始数据带入综合改进方法(3)中,
将(c1,c2)T带入MRE表达式中。不妨可先设α=0,然后令其在区间[0,1]变化且Δα=0.01,同时令m依次取1,2,…,n,利用matlab可得到MRE随m和α变化的图3。
再根据(8)式可得拟合序列并计算MRE。未改进模型与改进方法(3)拟合数据与相对误差、平均相对误差见表2。
从表2可以看出,综合改进模型无论是模拟精度还是预测精度均高于未加优化的模型以及仅对初始值或者背景值进行优化的模型。其中,预测精度的提升尤其显著,经典模型误差为0.033,而改进后模型仅为0.016,改进后的模型取得了良好的预测效果。
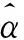
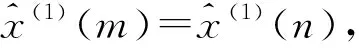
将三种改进方法和经典模型进行综合比较,可得到表3、图4:
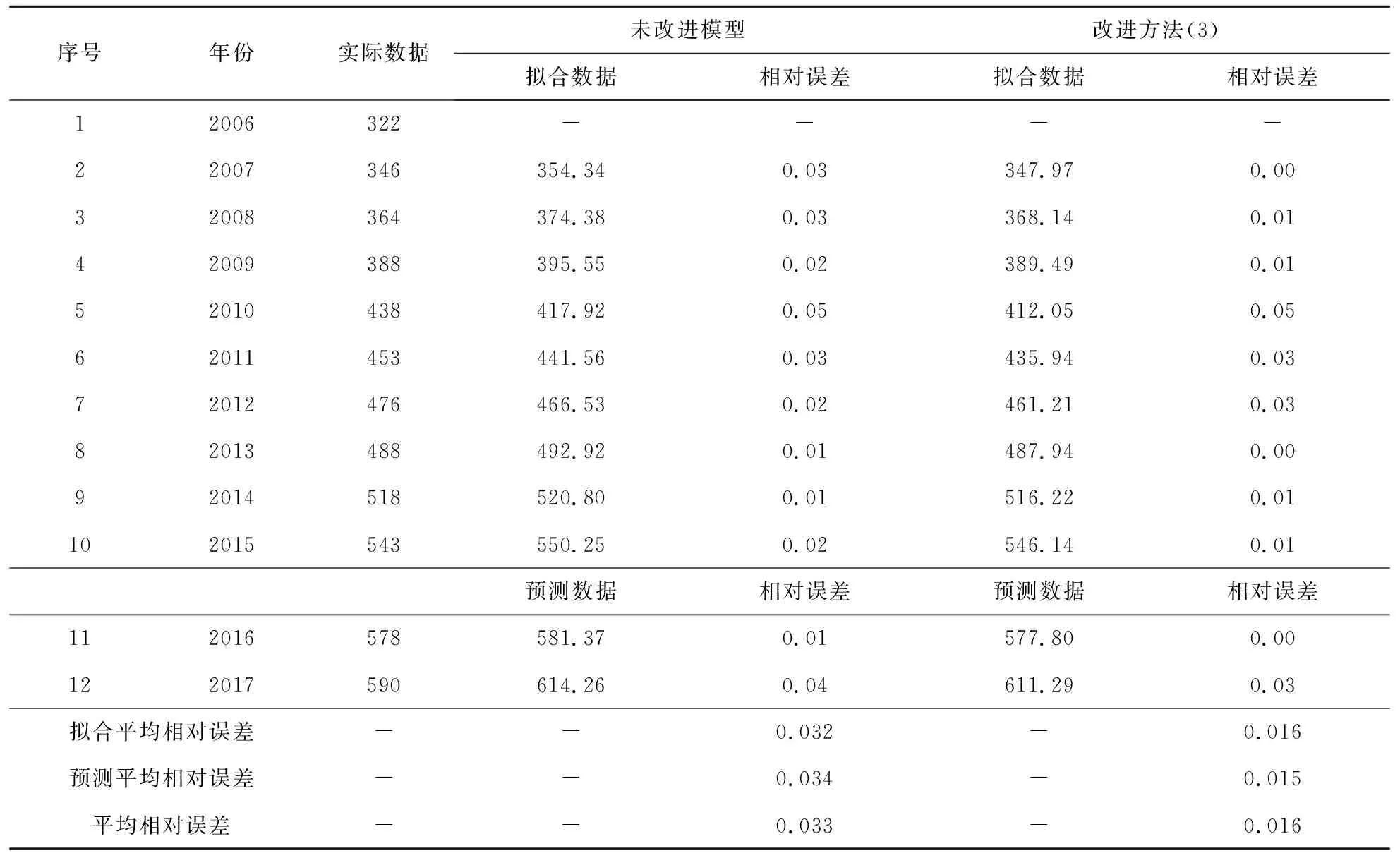
表2 中国国内石油年消费量预测(百万吨)
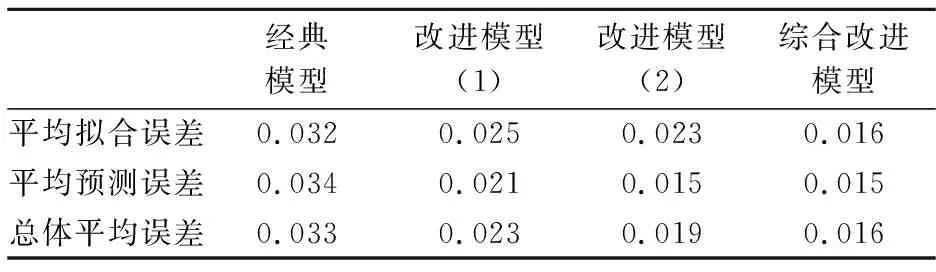
表3 经典模型及改进模型误差情况
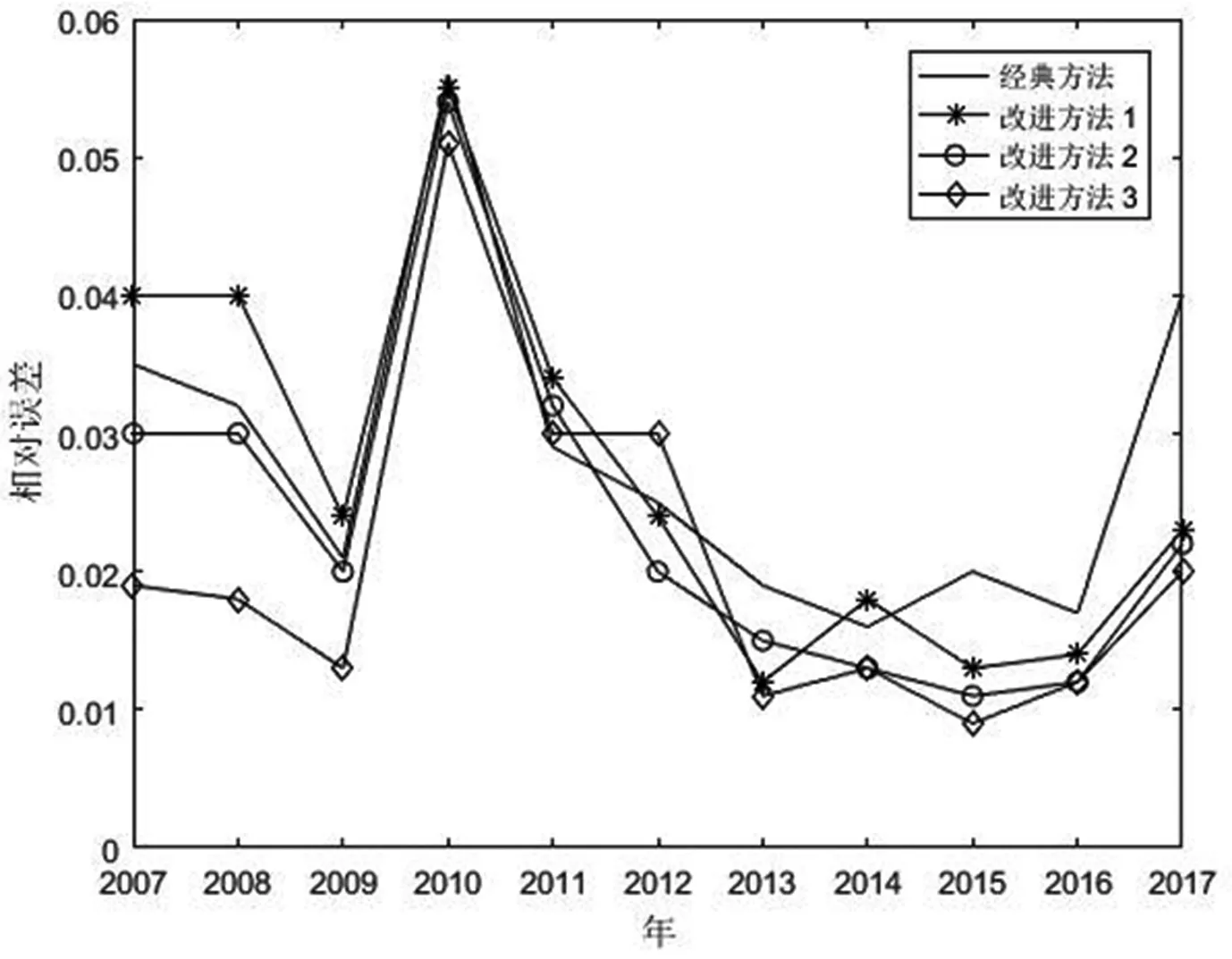
图7 2007~2017年四种方法相对误差
综合来看,改进方法(3),即综合改进方法,无论是拟合误差还是预测误差均低于经典模型以及其他两种改进方法。随着改进程度的深入,模型误差呈现出递减的趋势,验证了模型优化的有效性。
4 总结与讨论
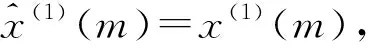
实际上,在建模过程中,变量越多的模型,预测精度往往越高。如果把模型初始值、背景值等都看作变量,优化的变量越多,得到的模型精度越高。所以通过优化多个变量和某种参数估计方法提高预测精度是未来的一个研究方向。

