基于多目标规划的飞机路径恢复最优化算法研究
胡玉真,张 耸
(哈尔滨工程大学 经济管理学院,黑龙江 哈尔滨 150001)
0 引言
在民航运输业中,航班日常运行较易受到天气、空中流量以及公司内部等诸多因素干扰而偏离原计划,出现不正常航班。不正常航班会给航空公司带来直接的经济损失和潜在的隐形损失。要彻底根除这些干扰带来的损失是不可能的,目前主要是通过对飞机等资源的重调度使得航班尽快恢复正常,尽量降低干扰带来的各种损失,这个过程称之为航班干扰管理[1]。
航班干扰管理问题一直受到国内外航空领域和运筹优化领域研究者的关注,经典的航班干扰管理问题是追求延误和取消总成本的最小化。Hu et al.[2]在2015年已经证明,当问题的目标包括最小化总的航班延误时间时,飞机路径恢复问题是NP难问题。以往的大部分文献,都尝试运用求解整数规划模型的相关方法(网络流算法、列生成算法、拉格朗日松弛算法)以及智能算法(如遗传算法、GRASP算法以及邻域搜索算法等)求解该问题。
最早是由Teodorovic et al.[3]运用分支定界算法求解3架飞机8个航班的航空运输网络在受到干扰后的飞机路径优化问题。Yan et al.[4]、Xu et al.[5]、Marla et al.[6]和Vink[7]分别建立了基于时空网络构建飞机恢复问题的整数规划模型。Eggenberg et al.[8]利用列生成算法使得飞机恢复问题得到解决,其中主问题是集合覆盖问题,而子问题是带边界限制的最短路问题,其中对每个飞机,都建立了一个基于时段网络的恢复网络。詹晨旭和乐美龙[9]设计了基于遗传算法的启发式算法求解分飞机路径恢复问题。Bisaillon et al.[10]对包括飞机路径和旅客恢复的航班调整问题,设计了邻域搜索算法,且目标为最小化相应的运营成本以及对旅客的影响,随后基于Bisaillon et al.[10],Sinclair et al.[11]在算法中添加了某些步骤,使得算法更有效。张力菠和鲍和映[12]针对飞机资源短缺、机场临时关闭导致的航班干扰状况,设计算法构建了离散时空网络模型,并用商业软件进行求解。Aktürk et al.[13]在航班恢复中考虑油耗和航行速度的权衡。Vos et al.[14]对每架飞机建立时空网络模型,并结合肯尼亚航空公司的实际数据进行案例分析和模拟仿真。胡玉真等[15,16]探讨了单架飞机受干扰后的飞机路径恢复问题的多项式算法。随后Hu et al.[17]添加参与恢复的飞机数量和最大延误时间作为优化目标,对飞机路径恢复问题进行多目标优化建模,并运用邻域搜索算法求解该问题。
但是上述很多算法都是指数级的,且无法从理论上证明求解方案的最优性或近似性。并且大部分文献为了使得模型具有较好的整数规划模型的性质,只建立单目标规划模型。有些即使建立多目标规划模型,也会运用线性加权的方式将目标整合为单目标形式。但是,航空公司日常运营比较复杂,纯粹单目标的优化解并不能真正反应航空公司航班运营恢复的实际情况,而运用多目标建模求解实际航班调整方案,可以使得航空公司运行控制中心根据航班计划和资源的实际情况从非劣解集中进行选择,更增加了航班计划和飞机路径恢复的灵活性。
如果飞机只是受到短时间轻度的干扰,不需要取消航班就能使得航班计划在当天恢复正常,那么运行控制中心的主要目的就是如何通过飞机交换、航班延误等调整手段降低航班的延误时间。按照中国民用航空总局的规定,航班延误时间超过30分钟,需要向旅客通报延误信息。因此,尽量降低最大的航班延误时间,会有效的改善航空公司的服务质量。另外,如何在保证航班延误时间较小的目标下,实现动用尽可能少的飞机资源,也更符合航班干扰管理的基本思想。
因此本文针对轻度航班干扰状况,以降低航班最大延误时间和参与飞机交换的数量为双重目标,对飞机路径恢复的多目标规划问题展开研究。本文在前期研究成果的基础上,结合航空公司日常运营的实际情况,研究在不正常航班出现后,以最小化航班最大延误时间和最小化参与交换的飞机数量为双层目标的飞机路径恢复的全局优化问题。首先根据常用的航班调整原则,分析问题的一些特点,揭示出以最小化航班最大延误时间为第一目标的问题全局最优解仅通过交换一次航班序列即可得到。并设计基于快速排序的组合构造算法求得最优解。然后分析在满足上层目标的所有最优解中,求解以最小化参与交换的飞机数量为目标的最优化问题可以等价为最小费用最大流问题,最后设计基于网络流的组合算法求得双层目标的飞机路径恢复的全局最优解。
本文的结构安排如下所示:第一部分对问题进行描述并结合相关假设建立多目标规划模型;第二部分基于假设对问题体现出的性质进行分析;在第三部分中设计了组合算法来解决该问题,并证明其能得到最优解;第四部分设计算例验证算法的有效性;最后,第五部分对本文进行了总结。
1 问题描述
本章研究多架飞机受到短时间干扰后飞机路径恢复的多目标优化问题(HOARP)。描述如下:已知同一个机场的若干架飞机受到干扰,其原计划执行的航班不能按照原计划进行出港,求如何使用飞机交换(用航班任务少的飞机与受到干扰的飞机交换)和航班顺延(根据受到干扰的飞机或者新交换的飞机可用时刻重新调整航班的出港时间)等手段重新调整航班使得航班能够在短时间内恢复正常,并分层实现航班干扰管理的双重目标:第一目标为最小化航班的最大延误时间,第二目标为最小化参与飞机交换的飞机数量。在满足上述目标的同时也需要满足以下约束限制:i)每个航班只能被一架飞机执行;ii)每架飞机只能执行一个航班序列,即得到一条飞机路径;iii)在当天宵禁结束之前,每个机场应该有足够的数量飞机停驻,且和原计划的数量一致,以不影响第二天的正常航班运行。
依据上述目标设置、约束限制以及相关的假设,基于连接网络建立如下多目标规划模型。
索引:
I飞机索引
F航班索引
r航班序列索引
s机场索引
集合:
P受干扰的和参与交换的飞机集合
F航班集合
R航班序列集合
S机场集合
R(f) 包含航班f的航班序列集合;f∈F
R(s) 落地机场为s的航班序列集合;s∈S
参数:
yri=0 表示航班序列r原计划被飞机i执行;r∈R,i∈P
trfi航班序列r被飞机i执行时,航班序列中航班f的延误时间;r∈R(f),f∈F,i∈P
ms按照计划在机场s应该停驻的飞机数量s∈S
Q1,Q2目标的优先因子
决策变量:
xri=1表示航班序列r由飞机i执行;否则=0;r∈R,i∈P
(1)
(7)
模型目标表示如下,其中公式(1)表示最小化第一目标为所有航班的延误时间最大值,公式(2)表示最小化第二目标为参加飞机交换的飞机数量,表达式(3)表示目标Z1的优先级远远大于目标Z2。
约束(4)表示每个航班都需要由一架飞机执行,约束(5)表示参与交换的每架飞机最多只能一条航班序列,约束(6)表示在每个机场应该有足够数量的飞机停驻,以至于不影响第二天的航班任务。
为了使得问题具有一些较好的性质、以及后续分析和算法设计的方便,现给出若干概念的定义如下。设航班集合为F={Fi|i∈P},Fi={fi1,fi2,…}表示原计划由飞机i∈P执行的航班序列。在航班序列{fiu,fi(u+1),…,fiv}中({fiu,fi(u+1),…,fiv}⊆{fi1,fi2,…}),如果航班fiu的出港机场与航班fiv的进港机场相同,则航班序列{fiu,fi(u+1),…,fiv}被称为航班环。

假设如下:i)受干扰的飞机以及参与交换的飞机都属于同一个机型,且干扰发生在同一个机场;ii)在航班计划中,所有的航班都可以正常出港,即原计划执行该航班的飞机在出港机场的可用时刻不晚于该航班的计划出港时刻;iii)本文采用的航班调整手段为飞机交换和航班延误,不包括航班取消、调机等措施;iv)无论是否进行飞机路径恢复,所有的飞机能在机场宵禁之前完成所有的航班;v)干扰时间窗的长度小于所有的航班环长度,即所有受干扰飞机执行航班的计划出港时刻的最小值到所有受干扰飞机的实际可用时刻的最大值之间的时间段长度小于所有航班环时间跨度的最小值。
在航班运行的过程中,可以分为若干个时间区间,某一个时间区间内,出港航班数量远多于进港航班,称为出港航班波;在另一个时间区间内,进港航班数量远多于出港航班,称为进港航班波。当干扰发生时,航空公司一般运用出港航班波结构,依次在延误航班发生的各个机场进行调度。首先,需要在发生干扰的机场利用出港航班波,寻找可用飞机集合(记为P′,P′⊆P),与受干扰的飞机P″⊆P进行飞机交换,这被称为交换阶段1。在交换阶段1之后,如果仍存在延误航班fik,∀i∈P,k=2,3,…,(注意航班序列{fik|i∈P,k=1,2,…}在飞机交换阶段1后,并不一定被飞机i∈P执行)。然后在航班fi2的出港机场,再次利用出港航班波寻找可用的飞机与执行航班序列{fik|k=2,3, …}的飞机继续进行交换。以此类推,直到在后续的航班序列不存在延误航班。
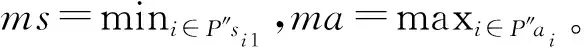
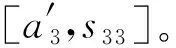
基于航班环和干扰区间的定义,则假设v)可以用公式表示如下:
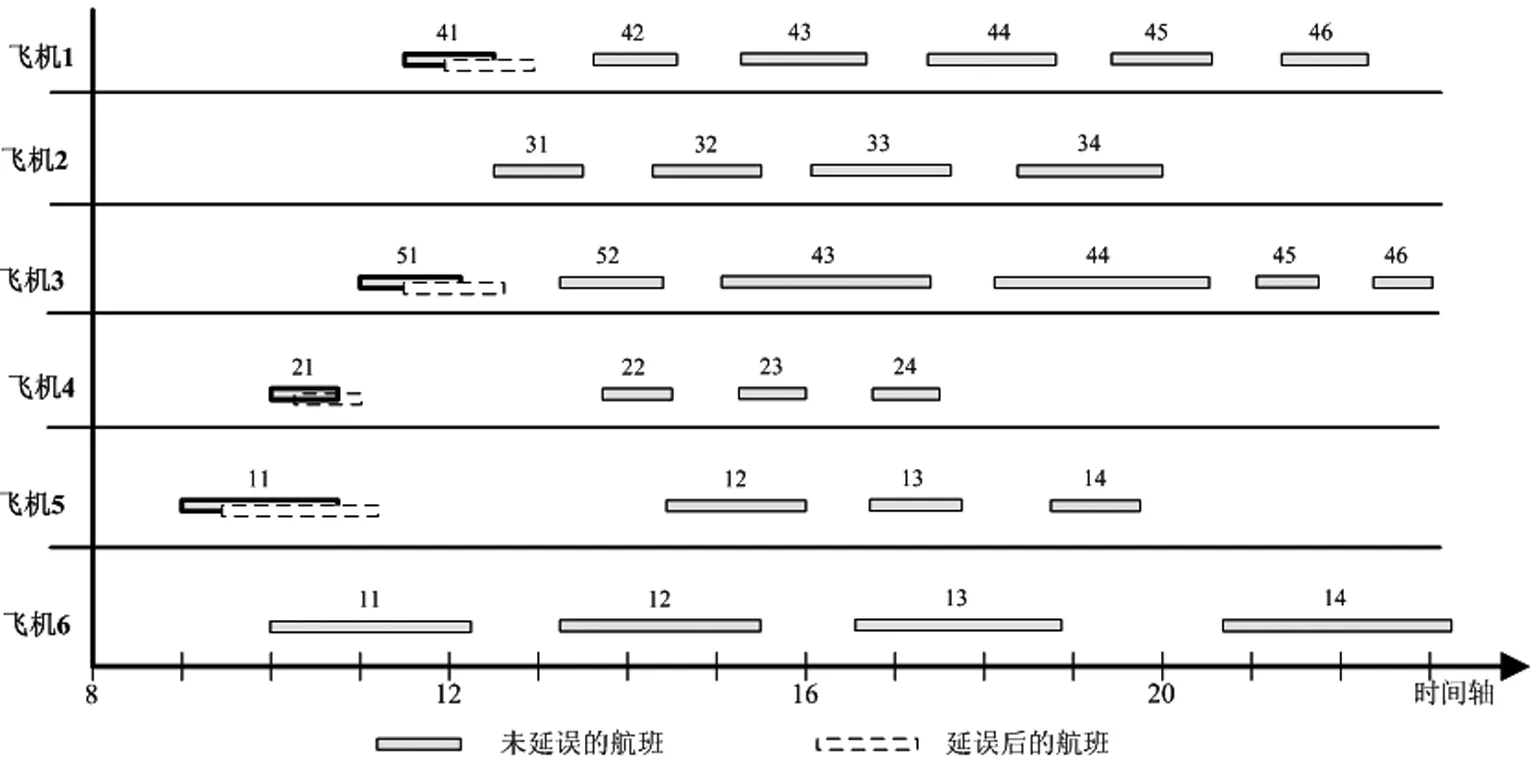
ma-ms (8) 其中c表示航班环,tc表示航班环的时间区间长度,即从航班环中首个航班的计划出港时刻到航班环中最后一个航班的计划进港时刻之间的时间跨度。 图1 交换/干扰区间示意图 在交换阶段1中,令可以参与飞机交换的交换区间集合记为IN,则按照飞机交换区间的定义、以及和干扰区间的关系,我们把交换阶段1中找到的飞机交换区间集合IN分为6类。 IN=IN1∪IN2∪IN3∪IN4∪IN5∪IN6 (9) IN1={ini|ai≤ms,ma≤si1,i∈P′} (10) IN2={ini|ai≤ms (11) IN3={ini|ms (12) IN4={ini|ms (13) IN5={ini|si1≤ms,i∈P′} (14) IN6={ini|ai≥ma,i∈P′} (15) 设SOLm表示在交换阶段m中得到的可行解集合,valuesol表示可行解sol∈SOLm的第一个目标值,则可以得到以下引理。 在以下的叙述中,设(inl,fi1)表示航班序列{fij|j=1,2,…}被飞机l执行,其中l,i∈P′;OPT表示问题的最优解集合;INsol表示在实际中参与飞机交换的交换区间集合。 由引理3和引理4得知,IN5和IN6集合中的飞机交换区间不会参与最优解中的飞机交换。可以通过在集合IN1、IN2、IN3和IN4中选取交换区间进行飞机交换。在下一部分将会介绍多项式算法求解飞机路径恢复的多目标规划。 根据Z1和Z2的分层结构,本文设计一种多项式时间算法(QSMCF)来求得多目标规划的最优解,然后给出算法的时间复杂度分析和算法的最优性证明。 QSMCF算法是在快速排序算法和最小费用流算法结合的基础上设计的多项式时间算法。在算法中,首先运用快速排序算法求得航班的最大延误时间valuemax,其次根据飞机和航班的匹配状态,建立网络图CN=(o,t,V,A,ω,y,b)。在网络图中,o和t代表网络流的起点和终点;V=I∪J,其中I和J分别代表飞机集合和对应的航班序列的集合;A=A1∪A2∪A3,其中A1={(o,i)|i∈I}代表飞机I开始被安排,A3={(j,t)|j∈J}代表所有航班序列已被飞机覆盖完毕,A2={(i,j),i∈I,j∈J},在A2中的每一条弧(i,j)∈A2代表飞机i∈I可能会被安排执行航班序列j∈J。对于每一条弧(i,j)∈A2,ωij代表飞机i执行航班序列j时首个航班的延误时间,即ωij=max{ai-sj1,0};yij是航班序列j是否是由原飞机执行的标示,=0表示航班序列j由原飞机i执行,=1表示执行航班序列j的飞机i不是航班序列j的原飞机;bij表示弧(i,j)∈A2的容量,且bij=1,∀(i,j)∈A2。对于弧(o,i)∈A1和(j,t)∈A3有yoi=0,boi=1,∀i∈I,yjt=0,bjt=1,∀j∈J。 算法QSMCF: 输入:IN1,IN2,IN3,IN4以及对应的航班序列 第1步运用快速排序算法分别对{ai|i∈P}和{sj1|j∈P}从小到大进行排序; 第2步设ai(1)≤ai(2)≤…≤ai(|P|),且sj(1)1≤sj(2)1≤…≤sj(|P|)1,sol={(i(k),j(k))|k=1,2,…,|P|},valuemax=max(i,j)∈solωij。 第4步设网络图CN′中从o到t的初始流为fl,令初始流的大小valfl=0; 第5步如果valfl=|P|,则转第8步,否则转第6步; 第6步建立增量网络图CN′(fl),并找到一条从o到t的最小费用增广路M,以及对应的最小费用yij,转第7步; 第7步设C(M)为增广路M中的最小弧容量,设θ=min{C(M),|P|-valfl},在CN′中沿M对fl增流θ,得新流fl,转第5步; 输出:solopt,value1QSMCF和value2QSMCF。 算法QSMCF的复杂度为O(|P|4)。首先,根据C.A.R. Hoare[18],第1步的复杂度为O(|P|log(|P|));第4~7步为最小费用路算法,其每次增流至少一个单位,因此需要经过至多|P|次找最小费用增广路并增流;而第6步中每次求最小费用增广路可以使用最短路算法,其计算量不超过O((2|P|+2)3);第7步中沿增广路增流过程的计算量不超过O(2|P|+2)。因此,计算得到QSMCF算法的复杂度为O(|P|log(|P|)+|P|×((2|P|+2)3+(2|P|+2)))=O(|P|4)。 设valuemax=max(i,j)∈so|ωij=ωi*j*=max{ai*-sj*1,0},我们首先根据ai*和sj*1将集合sol里的元素分为四个子集,并以此将对应的飞机集合I和航班序列集合J分别分为四个子集,然后根据各子集之间元素的数量比对关系用反证法分析证明出ai*sj*1是Z1的最优值。 定义1集合sol可以分为M1、M2、M3和M4四个子集。 如果ai*≥sj*1,子集如下所示: M1={(i,j)∈sol|ai M2={(i,j)∈sol|sj1 M3={(i,j)∈sol|sj*1≤sj1 M4={(i,j)∈sol|ai≥ai*,sj1≥ai*} 如果ai* M1={(i,j)∈sol|ai M2={(i,j)∈sol|ai M3={(i,j)∈sol|ai*≤ai M4={(i,j)∈sol|ai≥sj*1,sj1≥sj*1} 定义2飞机集合I分为A1、A2和A3三个子集;航班序列集合J分为B1、B2和B3三个子集。 如果ai*≥sj*1,则A1={i∈I|ai 如果ai* 引理5如果ai*≥sj*1,则|A1|=|M1|,|A2|=|M2|,|A3|=|M3∪M4|=|M3|+|M4|,|B1|=|M1∪M2|=|M1|+|M2|,|B2|=|M3|,|B3|=|M4|; 如果ai* 为了更精确的分析多目标规划用于航班干扰管理的效果,以及验证算法QSMCF的有效性,我们给出一个恢复规模为6架飞机的算例,具体航班计划信息如表1所示。在该算例中,飞机在各机场的最小过站时间为40分钟,各机场的宵禁时间为当天的24时。从表1中可以看出,飞机1、2受到干扰,可用时刻分别为12∶00和12∶10。如果没有其他飞机参与与飞机1和飞机2的交换,则航班序列S1={f11,f12,f13,f14}中各航班的延误时间分别为180分钟、119分钟、58分钟和0分钟,航班序列S2={f21,f22,f23,f24}中各航班的延误时间分别为132分钟、58分钟、56分钟和0分钟,即所有的航班都能在宵禁之前完成生产任务。我们需要做的是在机场PEK寻找其他可用的飞机用来与飞机1和2交换,以降低最大的航班延误时间,并使得参与交换的飞机数量最少。 表 1 航班计划表和飞机状态信息 在第一阶段调整时,首先由表1中6架飞机的可用时刻和首个航班的计划出港时刻之间的关系,找到飞机交换区间,IN1=ø,IN2={in6},IN3={in4,in5},以及IN4={in3}。在进行飞机交换时,每个航班序列中的所有航班都和首个航班是被同一架飞机执行,而且这些航班序列被任何一架飞机执行,都能在宵禁之前完成生产任务。 图2和图3分别给出了sol中飞机和航班序列首个航班的匹配信息以及算法得到的飞机路径优化解solopt中飞机和航班序列首个航班的匹配信息。图4则显示了solopt中所有航班信息。在图2和图3中,弧左边是飞机交换区间信息以及对应的飞机的可用时刻,弧右边是飞机交换区间后面的航班序列中首个航班信息、首个航班的计划出港时刻、以及如果由弧所指的飞机交换区间对应的飞机执行得到首班延误时间。例如,在图2中,飞机交换区间中飞机和航班序列的匹配为:(in1,f41)、(in2,f31)、(in3,f51)、(in4,f61)、(in5,f21)和(in6,f11),共有4架飞机(飞机3、4、5、6)参与与受干扰飞机1和2的交换,至少有三个航班(f41、f51、f61)发生延误,延误时间分别为30分钟、30分钟和20分钟,且最大延误时间为30分钟。而图3中,飞机和航班序列的匹配为:(in1,f41)、(in2,f31)、(in3,f51)、(in4,f21)和(in5,f11),共有3架飞机(飞机3、4、5)参与与受干扰飞机1和2的交换,从图4可知,solopt中共有四个航班(f11、f21、f41、f51)发生延误,延误时间分别为30分钟、22分钟、30分钟和30分钟。从图2和图3的对比可以看出,本文的算法在保证航班的最大延误时间不变的情况下,能够最大程度的降低参与交换的飞机数量,这更符合航班干扰管理的原则。 图2 Z1的最优解中首个航班与飞机的匹配信息 图3 本文算法得到的最优解中首个航班与飞机的匹配信息 图4 本文算法得到的最优解 在本文中,我们考虑了同一机场中多架飞机受到干扰后的双目标航班调整问题(HOARP),该问题目标为最小化航班延误时间最大值和最小化参与交换的飞机数量。并结合分层序列法的思想求解该问题。基于航空公司在实际的航班调整中一般利用航班波的特点,我们分析了多目标规划问题的一些性质,并且总结出第一个目标的最优值在第一阶段调整后就能得到。然后设计了一个基于快速排序算法和最小费用路算法的多项式算法(QSMCF),得到问题的最优解。结合HOARP问题的结构特点,本文分析出QSMCF的复杂度O(n4),其中n为参与干扰恢复的飞机总数量。最后给出一个小算例验证了算法的有效性。 在后续的研究工作中,我们将会针对以下几个方向进行研究:首先,我们会试图对不同机场的飞机受到干扰后的航班调整问题研究多项式时间算法,当受干扰的飞机处于不同的机场时,由于后续航班序列可能会出现机场的交叉,交换阶段会很难界定,同时问题的性质也会发生改变;其次,通过将旅客恢复网络潜入到飞机网络中的方法求解飞机和旅客同时恢复的问题将会比较有意义;最后,本文主要是寻找飞机受到干扰后的路径恢复最优解,属于被动处理干扰,在实际情况中修改航班计划使其更具有鲁棒性也是很热点的一个研究方向。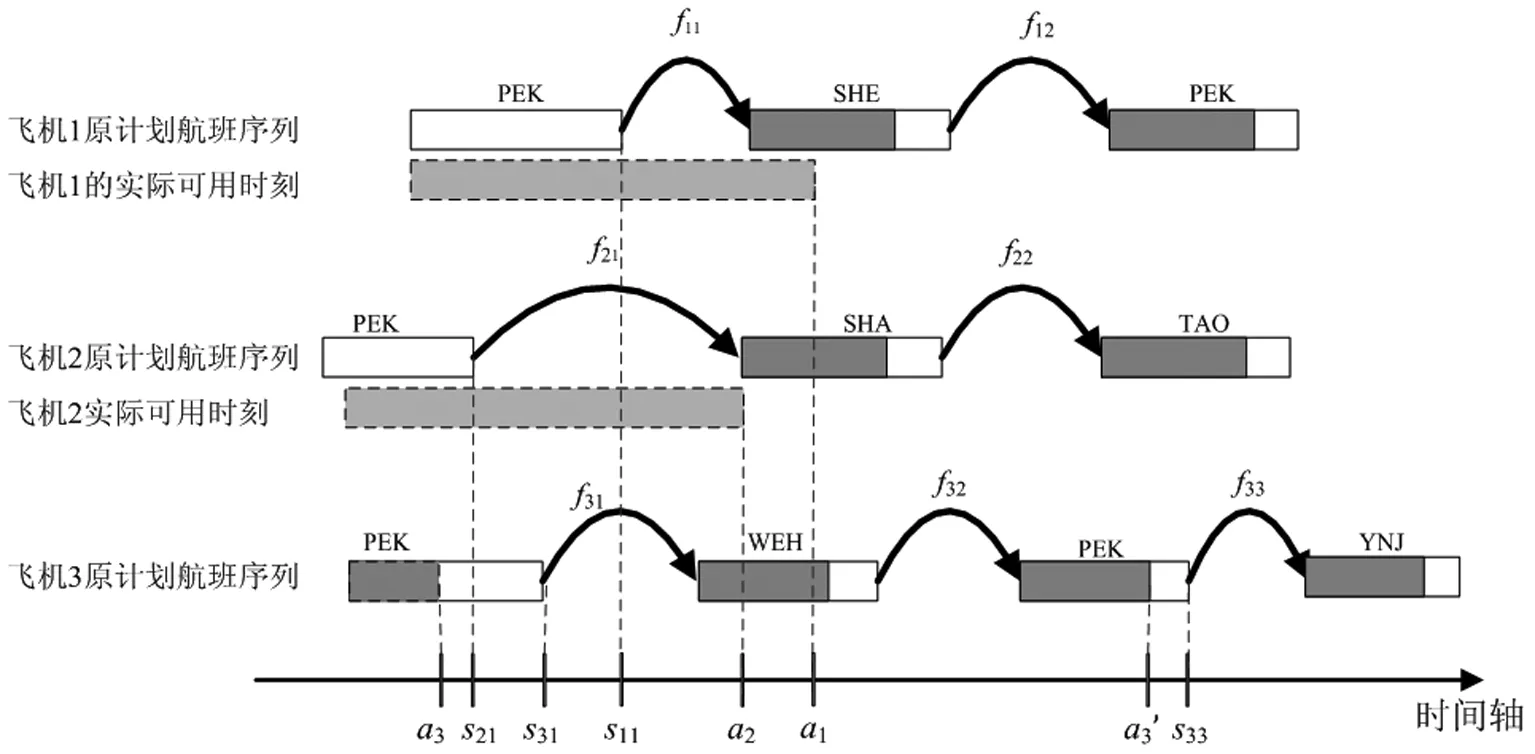
2 性质分析

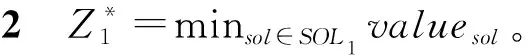


3 算法设计
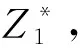
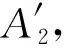

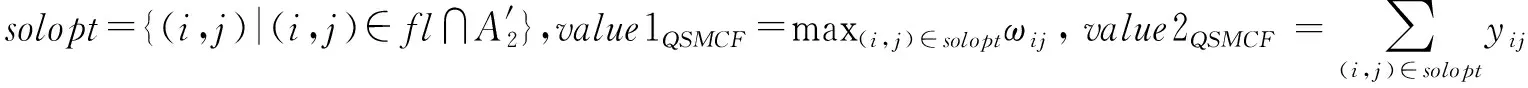


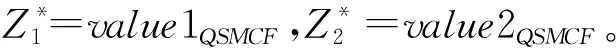
4 算例分析



5 结论

