基于机器学习算法的混凝土抗压强度预测模型
朱晓路,陈文翰
(杭州隆欣建材有限公司,浙江 杭州 310024)
混凝土的抗压强度是混凝土质量评价的重要指标[1-2],而混凝土抗压强度的测试费时且复杂,另存在着各种多变的环境因素和技术因素可能导致结果滞后,对现实生产的指导性降低[3]。近些年来,关于混凝土的抗压强度的预测已经迅速发展起来[4]。季韬将人工神经网络应用于混凝土抗压强度预测,把粉煤灰量、胶凝材料量、骨料浆体厚度等数据作为参考因素预测抗压强度[5]。杨松森以模糊系统方法对混凝土进行无损检测抗压强度预测,回弹值、碳化深度值、含水率、超声值作为参考因素[6]。许杰淋等人探究混凝土中水泥、矿渣粉、粉煤灰、水、减水剂、粗集料和细集料含量等原材料对混凝土抗压强度的影响,达到4.3%左右的平均误差[7]。但在实际工作中,由于各种原料用量非完全独立因素,相互间存在一定的关联关系,如水与胶粘材料的比例,粗骨料与细骨料的比例等存在确定性关系,这对预测的准确性产生了一定的影响。因此,本文将应用灰色关联分析法,将砂率、水胶比和水灰比作为ANN输入项,研究其对混凝土的抗压强度预测精度的影响,从而提高混凝土抗压强度的预测精度。
1 GA-ANN模型与灰色关联分析
1.1 BP神经网络的算法基础
图1是一个四层的人工神经网络[8],一个输入层,两个中间层和一个输出层。基于梯度搜索技术的反向传播算法被用于优化人工神经网络的权值和阈值,并最终确定人工神经网络的结构。网络中神经元xi的输出由下式计算得到:
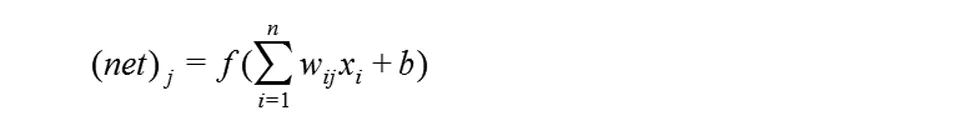
这里,(net)j是该神经元的输出,wij是权值,b为阈值,n为神经元的个数,f为激励函数,其表达式如下:
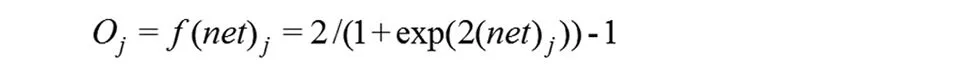
BP-ANN主要包含两个过程:第一个过程,从输出层输入变量,通过激励函数运算,经过输入层、中间层最后到达输出层;第二个过程,网络的输出与目标值进行比较,得到误差值。网络调节权值阈值直到误差达到预先设定的目标。反向传播算法在最速下降方向调节网络权值,从而加速收敛。
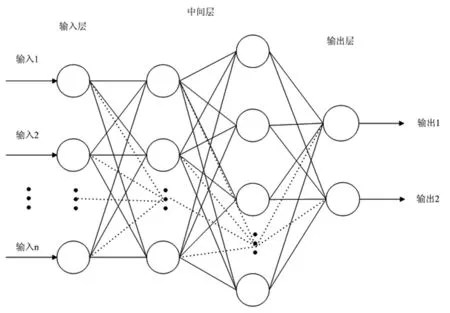
图1 人工神经网络结构图
1.2 遗传算法概述
遗传算法是基于自然界进化和选择的理论发展而来的,自1975年发明以来越来越多的用于最优化问题求解[9]。遗传算法中最重要的四个因素为染色体、适应度值、选择和交叉变异。
1.2.1 染色体
遗传算法通过编码染色体产生初始种群,每个个体中包含了人工神经网络中所有的权值和阈值,在网络结构已知的情况下,就可以构成一个结构、权值、阈值确定的神经网络。
1.2.2 适应度函数
适应度函数的作用是计算种群中个体的适应度值。先设定一组权值和阈值,计算目标值和预测值之间的误差,误差的总和为个体适应度值。适应度函数如下:

这里n是网络输出节点数,yi是神经网络第i个节点的期望输出;oi是第i个节点的预测输出;k为系数。
1.2.3 选择
选择操作的方法主要有轮盘赌法,竞标赛法等。本实验中采用了轮盘赌。用法轮盘赌选择,每个个体类似于轮盘中的一小块扇形,扇形的大小与该个体被选择的概率成正比。扇形越大的个体被选择的概率越大,即适应度越大,个体被选择的概率越大。个体被选择的概率pi通过下式表达:

Fi是个体适应度值,由于适应度值越小越好,所以在个体选择前对适应度值求倒数;k是系数;N是种群个数。
1.2.4 交叉和变异
交叉是指把种群中的个体两两配对,产生父代,并将父代个体的部分结构加以替换重组而生成新个体的操作。变异是对群体中父代个体串的某些基因座上的基因值作变动。第k个染色体和第l个染色体在j位点发生的变异如下:

这里b是0到1之间的随机数。
选择和交叉并没有新个体生成,在基因层面生成新个体需要通过变异操作实现,变异操作方法如下:
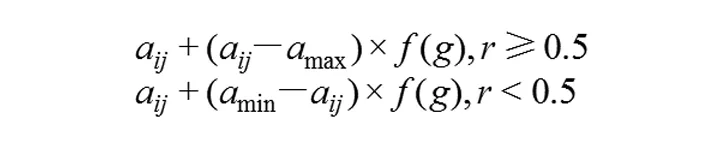
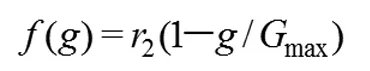
基因被储存在染色体中,染色体通过复制遗传到下一代,也可以通过交叉和变异产生新个体。遗传算法中,染色体是一系列被用于寻找最优解的“基因”,遗传到下一代的概率是通过适应度值确定的,适应度值高的个体被选择遗传到下一代的概率更大。
1.3 基于遗传算法的BP人工神经网络
遗传算法优化BP神经网络算法流程如图2。
遗传算法优化BP神经网络分为BP神经网络结构确定、遗传算法优化和BP神经网络预测3个部分。其中BP神经网络结构确定部分根据拟合函数输入输出参数个数确定BP神经网络结构,进而确定遗传算法个体的长度。遗传算法优化使用遗传算法优化BP神经网络的权值和阈值,种群中每个个体都包含了一个网络所有的权值和阈值,个体通过适应度函数计算个体适应度值,遗传算法通过选择、交叉和变异操作找到最优适应度值对应个体。BP神经网络预测用遗传算法得到最优个体对网络初始权值和阈值赋值,网络经训练后预测函数输出。
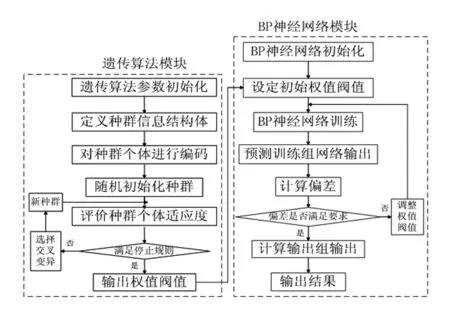
图2 遗传算法优化的BP神经网络模型结构图
2 数据分析及结果讨论
2.1 数据来源
本文数据取自杭州某混凝土有限公司连续一个季度的实际生产数据。因该公司的原材料来源比较固定,原材料的结构、类型、材质几乎保持不变,所以可忽略上述因素不同而对强度分析造成的影响。本文选择原材料用量(单位:kg/m3)作为网络输入层。表1中前150组数据用于灰色关联分析和模型训练,后24组数据用于模型输出预测。

表1(续)
2.2 灰色关联法分析混凝土强度的关键性影响因素分析
混凝土配合比设计时,各种原料用量非完全独立因素,原材料用量间存在一定的比例数量关系与混凝土强度有直接关联,比如:比例关系包括水胶比、水灰比、砂率。因此需要将上述关联性纳入到人工神经网络的输入层的选择过程中,本文将水胶比、水灰比、砂率同时作为输入项进行考察,以利充分挖掘输入量与预测输出量的复杂关联关系,从而减小预测误差。
其中水胶比为每立方混凝土用水量与所有胶凝材料用量的比值。水灰比为拌制水泥浆、砂浆、混凝土时所用的水和水泥的重量之比,砂率为砂的用量比上砂和石子的总用量。
设定:表1中前150组数据,水泥、粉煤灰、矿粉、碎石、清水、砂、回收水、外加剂、砂率、水胶比、水灰比作为比较数列Xi(t),混凝土抗压强度作为参考数列X0(t),分辨系数设为0.5,探究11种输入因素与试块强度的关联系数、关联度,结果见表2。

表2 输入因素关联系数与其关联度
如表2所示,150组数据中,各输入项的关联系数都在50%以上,每个因素的150个关联系数的递增不明显,比较集中的分布在关联度左右,水胶比、砂率、水灰比、与混凝土抗压强度的关联度分别高达0.89、0.85、0.84,说明其对混凝土抗压强度都有较高影响。所以本文在以前的影响因素上加入了砂率、水灰比、水胶比,将其作为网络的输入项。
2.3 GA-ANN预测混凝土强度结果讨论
本节将选择不同输入层研究其对GA-ANN输出及混凝土抗压强度预测的影响。取训练组数为150组与输出组数为24组,隐含层节点为数11。
1)组:输入层为水泥、粉煤灰、矿粉、碎石、清水、砂、回收水、外加剂、砂率、水胶比、水灰比,输出层选择混凝土试块28天抗压强度。
2)组:输入层为水泥、粉煤灰、矿粉、碎石、清水、砂、回收水、外加剂,输出层选择混凝土试块28天抗压强度。
以均方根误差(RMSE)和平均相对误差及误差标准差来评价两组预测结果的准确性。
其中,RMSE是预测值与真值偏差的平方和与预测个数n比值的平方根,它能够很好的反应出测量的精密度,其值越小越好。公式如下:

以平均相对误差表明测量方法本身的稳定性,平均相对误差越小说明总体的混凝土抗压强度真实值与模拟值差距越小,计算公式如下:

公式中,ti是混凝土抗压强度, Oi是模拟值; N是总数据个数。预测结果如表3所示。

表3 混凝土抗压强度预测
如表3所示,1)组试验得出的包含水胶比、水灰比、砂率的相对误差总体来说都小于2)组,2)组未包含上述比例关系。通过对其RMSE值进行分析得出这三个比例关系的将预测精度由2.06提升至1.39,通过对平均相对误差及误差标准差的分析得出该数据较之于未包含比例关系的所得出的预测强度的稳定性高,可靠性好,如表4所示。

表4 预测误差分析
可见最合适的输入项为水泥、粉煤灰、矿粉、碎石、砂、清水、回收水、外加剂、砂率、水胶比和水灰比,前8项是每方混凝土用量(kg/m3),后3项是比率,总共11项。将这三种比例关系加入到基于遗传算法人工神经网络后的输入项后较之于未包含这三种比例关系的BP神经网络模型,它的平均误差由4.33%降低为3.20%,大幅提升了预测混凝土抗压强度的准确度。
3 结论
本文用灰色关联分析法为基础,对混凝土强度的影响因素进行了分析,发现混凝土抗压强度受到水泥、粉煤灰、矿粉、拌合用水等原料用量的影响,同时由于用量间有相互依存性,水胶比、水灰比、砂率也与混凝土抗压强度有较强的相关性,进而,本文将砂率、水胶比、水灰以及各类原料用量作为GA-BP-ANN模型输入层,预测混凝土强度,预测误差为2.18%,比没有选择水胶比、水灰比、砂率的BP神经网络预测效果好。

