一种用于乳腺电阻抗扫描检测的目标体深度信息提取方法研究

徐 帆，刘本源，史学涛，董秀珍，季振宇

（空军军医大学军事生物医学工程学系医学电子工程教研室，西安 710032）

0 引言

生物电阻抗成像是一种以组织电阻抗分布为目标的图像重建技术，可实现对器官组织功能的无创检测[1-2]，研究表明该方法可应用于癌症的早期检测，乳腺电阻抗扫描（electrical impedance scanning，EIS）成像检测已被证实在乳腺癌早期检测中具有应用前景[3-4]。乳腺EIS 检测时所获取的是被测区域组织阻抗分布的二维灰度映射图像，由于癌组织和正常组织间电阻抗特性存在显著性差异，如果检测电极阵列覆盖区域下存在异常阻抗扰动区域（称之为感兴趣目标），则这些检测电极单元相比周围其他电极单元会获取较大的电流信号，对应在二维映射灰度图中呈现“亮团”特征，结合图像特征分析等数据挖掘技术，可以判别检测区域是否有癌包块存在[4-6]。乳腺EIS 临床应用研究的深入对数据信息挖掘工作提出更高要求，其中提取感兴趣目标体（癌包块）的立体定位信息就是研究目标之一。癌包块的立体定位信息主要包含平面相对位置信息和深度信息，这些信息对于乳腺癌状态的辅助诊断具有重要价值。例如在乳腺癌新辅助化疗过程中需要对癌包块的状态变化进行监测时，就要关注癌包块立体定位信息的变化[7]。目前，EIS 二维映射灰度图中的“亮团”虽然可以直观反映感兴趣目标体的平面相对位置，但不能反映目标体的深度信息。如果能从现有检测信息中挖掘提取目标体（癌包块）的深度信息，将会进一步拓展乳腺EIS 的应用范围。

利用EIS 检测数据对目标体深度信息提取具有一定难度，目前尚处于探索研究阶段。西门子公司的Scholz 提出 SF-MUSIC（space-frequency multiple signal classification）算法，目标体被等效为一个“多极信号源”模型，其本质仍然依赖Assenheimer 等提出的“双极模型”，所以算法缺乏一般性和灵活性[8]。韩国Seo 等[9]进一步提出了“双层球面模型”，并在仿真模型上验证了对目标体深度信息的评价性能，但无法直接用于EIS 实测数据。国内，东南大学张峰等[10]提出EIS 成像完备参数提取算法，其本质是通过求解约束优化问题获得肿瘤的相关参数信息，算法的性能在数学仿真模型上得到了验证。综上，乳腺EIS 检测中对感兴趣目标体深度信息进行提取是准确检测肿瘤后对其定位信息的进一步挖掘[11-12]，是对EIS 检测信息深入挖掘的难点，目前研究多处于算法仿真阶段，尚无成熟方法。

本课题组在开展利用乳腺EIS 进行早期乳腺癌检测的研究基础上，尝试开展乳腺EIS 技术在乳腺癌新辅助化疗疗效评估中的应用研究，因此需要关注感兴趣目标体的深度信息[7]。为此，本文在前人研究的基础上，从乳腺EIS“双层球面模型”的数学模型推导出发，提出可用于EIS 实测数据的目标体深度评估方法，并利用物理模型实验系统进行验证和分析讨论。

1 乳腺EIS 检测原理及等效建模

进行乳腺EIS 检查时，被测者手握激励电极（参考电极），将检测电极阵列置于乳房表面，如图1（a）所示。如果检测电极阵列的电势为地电势，对激励电极施加一定的电压，那么电流通过人的手臂到达高电导率的胸肌组织，这样就可以将大面积的胸肌组织看作是一个等电势的平面，胸肌组织表面和检测电极就构成平行板电容器，它们之间会产生电场。因为健康的乳房中存在大量的脂肪组织，所以可以理想认为所形成的电场是均匀的，如果乳房中存在癌变组织，该组织就会在均匀电场中产生扰动，具体表现为该部位所对应检测电极单元上的电流值增加[4]。

建立乳腺EIS 数学模型时，假设胸大肌为一个等电势面，电势值等于激励电压，检测电极阵列面为地电势；乳腺正常组织看作具有均一阻抗特性的背景，癌包块（目标体）与正常组织间电阻抗特性具有显著差异。

如图1（b）所示，设人体三维空间为Ω，癌包块（目标体）为D，检测电极平面为Г，激励电极表面为γ，σ+iωε 为复电导率，v（r）为指向边界外侧的单位法向量，则位于人体三维空间Ω 内的任意一点r=（x，y，z）处的电压V（r）满足下列边界方程组：

图1 乳腺EIS 检测原理及等效模型

2 感兴趣目标体深度信息近似求解

2.1 建立“双层球面”等效模型

由于检测电极平面Г 对感兴趣目标体产生的扰动电流敏感检测区主要集中在该平面下方的区域中，本文将电场分析的感兴趣区域定义为如图2 所示的半球形区域内。

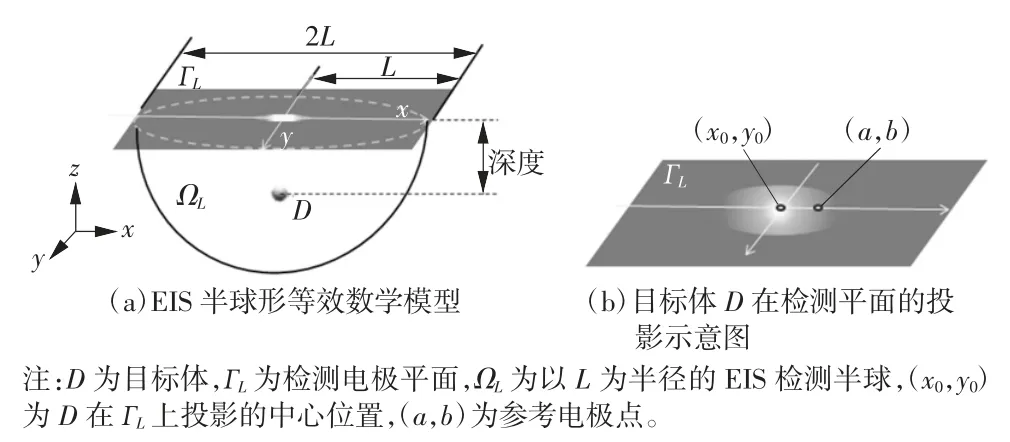
图2 EIS 检测乳腺内部的数学模型示意图

如图 2（a）所示建立 x，y，z 坐标系，设检测电极平面 Г 的中心点为原点（0，0，0），同时设其边长为2L，则半球形区域的半径为L。此时，方程组[公式（1）]求解的约束条件设置如下：

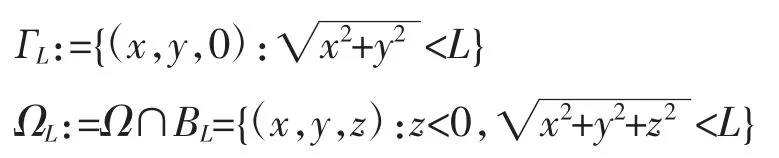
式中，BL为以原点（0，0，0）为中心点、以 L 为半径的球体，则ΩL为EIS 检测半球。此时设置目标体D 位于ΩL内，则将正常组织、病变组织的复电导率τ1、τ2定义为

则图2 中的各处电压满足下列方程：

式中，g（r）为流出检测电极板的电流密度。

假设乳腺中没有病变组织，则相应电压和电流参数（用'表示）满足：

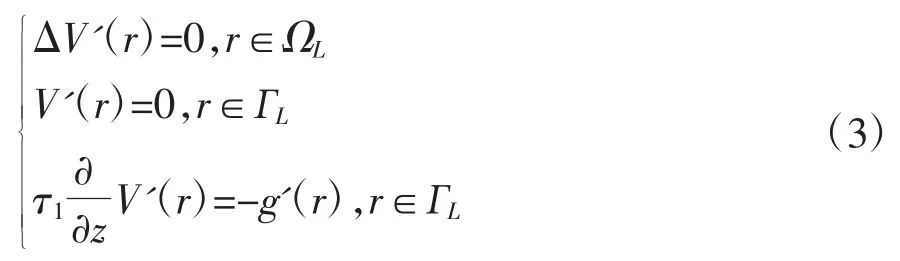
式中，g'（r）为乳腺中没有病变组织的情况下检测电极处的电流密度。

2.2 利用ΓL 平面上的信息表示病变区域D

本部分将利用检测电极平面的电流信息及相应电极单元的位置信息表示感兴趣目标区域的深度，具体实现过程如下：

将格林公式代入公式（3）。设 Φ（r，r’）是无限空间内的格林公式的解。其中ΔΦ（r，r’）=δ（r-r’），r∈ГL，r’∈ΩL。

根据格林公式对上述方程组[公式（2）和（3）]做了一系列推导，参见文献[9]。推导的最终目的是用ГL平面上的电流来表示病变区域D 的各种信息。经推导化简之后得到：

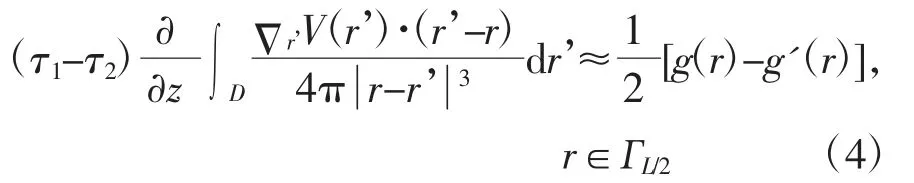
在 D 是球体或接近球体时，定义（x0，y0）为 D 在Г 上投影的中心位置，公式（4）可以进一步化简为

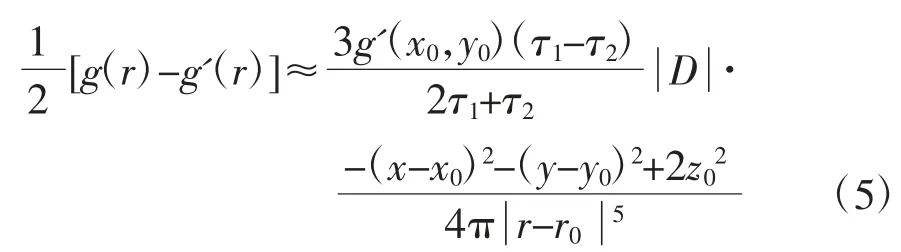
设置参考电极点（a，b）为 Г上任意一点，设 d 为该点到目标体 D 在 Г 上投影的中心位置（x0，y0）的距离，则D 的深度z0可通过以下公式得出：

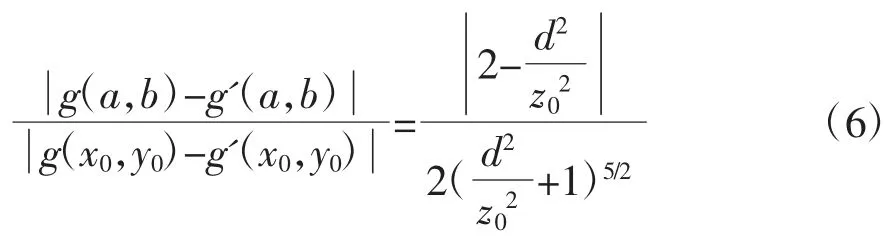
目标体深度z0指检测电极面距离目标体中心处的距离。虽然根据以上公式可以对目标体D 的深度z0进行测算，但该公式是在仿真模拟的条件下得到的，部分条件在实际应用中无法获得，需要近似替代。

3 利用实测数据实现深度信息的提取

从仿真计算模型中得到的目标体深度计算公式还不能直接在EIS 实测数据中应用，需要使用实测数据和实测条件对公式（6）中的参数进行替代或近似表达。EIS 实测数据采集到的是检测电极单元上的电流值，当检测电极单元的面积确定时，利用电流值i 替代公式（6）中的电流密度参数g，可得到以下公式：

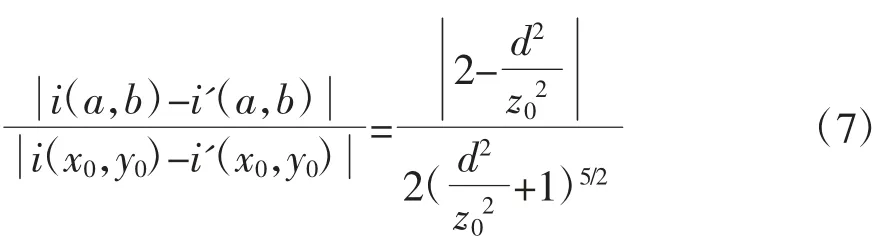
在此基础上，本研究进一步分析了采用EIS 实测数据对公式（7）中i'（x0，y0）、i'（a，b）、i（x0，y0）及i（a，b）参数值进行表达的方法，具体如下。

3.1 对i'参数的近似

在仿真计算分析时i'表示检测目标不存在时电极面上的电流密度，但在实际应用情况下i'是无法测出的，即EIS 实际应用于乳腺癌包块检测时，无法获得目标体（癌包块）不存在时的检测电流值，需要用近似参数替代公式（7）中的i'。

结合仿真计算分析可知，由于目标体D 不存在时所测结果相当于检测区域中全部为均匀正常组织时对应的结果。在图3（a）中正常组织的检测结果与二维灰度成像中的黑色区域相对应，所以可用黑色区域所对应的测量数据的平均值Imean近似替代i'（x0，y0）。该近似替代方法可用图3（b）的电流测量值三维分布图更直观地说明，即用平坦区域数据的平均值近似替代i'（x0，y0）。

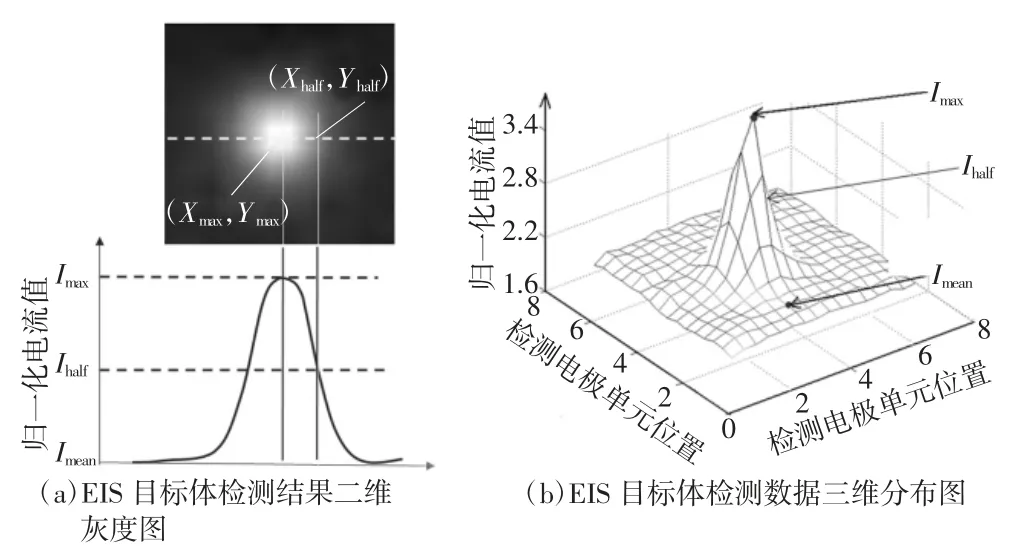
图3 EIS 检测结果二维灰度图及检测数据三维分布图

公式（7）中i'（a，b）表示目标体D 不存在时Г 平面上坐标（a，b）处的测量值，理论上当目标体不存在时测量平面上电流值近似均匀分布，所以可以认为i'（a，b）与i'（x0，y0）值相等。

3.2 确定坐标（x0，y0）及其对应的 i（x0，y0）参数值

在仿真计算模型中（x0，y0）为检测目标体 D 在检测电极面上投影区的中心位置坐标值（如图2 所示），该坐标对应最大检测值。如图3 所示，在实际测量数据中，i（x0，y0）可用二维灰度图中“亮斑”区域的最大值Imax替换，进而可确定该最大值处对应的电极单元坐标值（Xmax，Ymax），即用（Xmax，Ymax）替代（x0，y0）。

3.3 确定坐标（a，b）及其对应的 i（a，b）参数值

坐标（a，b）定义为参考电极位置，但（a，b）的位置如何选择在仿真计算模型中并没有指出，因此将EIS实际测量值应用于公式（7）时，需要确定（a，b）的位置才能获得i（a，b）。如图3 所示，如果（a，b）位置远离（x0，y0），则i（a，b）的值处于测量数据平坦区，其值与i0接近，而与病变包块引起的电场扰动区无关，因此（a，b）应选择在目标体投影区范围内。按此原则，本研究按照距离（x0，y0）的位置，选择了 3 种确定参考电极的方式，如图4 所示，参考电极点距中心位置（x0，y）0的距离分别为和2 倍的电极间距。为了减少误差，对于每种设置模式，i（a，b）都是用周边4 个点的平均电流值计算得到。

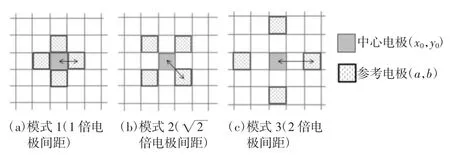
图4 参考电极点的3 种设置模式

4 物理模型验证

采用本课题组研制的EIS 硬件检测设备并结合盐水槽建立物理模型实验平台，在设定实验条件下获取EIS 实测数据，并利用实测数据验证本文提出的EIS 目标体深度信息提取方法的性能。

4.1 物理模型实验平台建立及实验条件设置

基于EIS 检测原理设计了盐水槽物理模型实验平台，如图5 所示。该系统包括EIS 硬件采集系统和盐水槽模型[13]。检测电极阵列为8×8 电极单元，电极单元边长为3 mm、间距为1 mm，有效检测电极平面形成32 mm×32 mm 的区域。盐水槽中注入一定电导率的NaCl 溶液模拟乳腺正常组织，当在激励电极施加一定的激励电压时，检测电极的电势为地电势，这样就在两电极之间构建了一个电场模型。若在NaCl 溶液中加入电阻率不同的“检测目标体”就改变物理模型内部均匀电场的分布，从而引起电场的扰动。本研究中用琼脂块模拟乳房中的病变包块，设置NaCl 溶液的电导率为0.05 S/m，设定琼脂的电导率为0.3 S/m，约为背景溶液电导率的6 倍。琼脂块的直径及其与检测电极阵列间的距离（目标体深度）可以在实验中进行设定。根据乳腺癌TNM 分期，T1 期的肿瘤最大直径不大于20 mm，因此本实验中将琼脂块直径设置为4、12、20 mm。按照检测距离（深度）由近及远的方式移动目标体，直至目标体无法被检测为止。

4.2 实验数据处理

按照实验条件设置，目标体放置盐水槽后，启动EIS 检测设备可采集实测数据，数据处理过程如下：

（1）将目标体置于固定深度位置处，通过多次测量，获得该位置处的实测数据平均值。进一步按照本文第3 章节关于i'（x0，y0）、i'（a，b）、i（x0，y0）、i（a，b）参数的确定方法获取相关参数值，利用公式（7）进行目标体深度（目标体深度指检测电极面距离目标体中心处的距离）信息估算。

图5 EIS 目标体深度检测物理模型实验

（2）按照图4 所示的3 种参考电极设置模式，分别计算不同参考电极模式下的深度信息参数。

（3）改变检测目标体大小及其在盐水槽中的深度，通过多次测量获得多组深度评价数据，并计算深度参数均值及标准差。

4.3 实验结果及分析

4.3.1 不同目标体的EIS 检测结果

将直径为4、12、20 mm 的琼脂块分别置于物理模型进行EIS 检测，并逐渐增加检测深度，直至无法检测，EIS 检测结果如图6 所示。可见检测目标体的体积会影响EIS 有效检测深度范围，即大目标可检测的深度较深，小目标可检测的深度较浅。如对直径4 mm 的目标体，EIS 的有效检测深度范围为15 mm以内；而对直径20 mm 的目标体，EIS 的有效检测深度范围为25 mm 以内。因此，在对本研究提出的深度信息检测方法进行验证评价时，在目标体的有效检测深度范围内进行。

图6 不同体积目标体在不同检测深度时的EIS 物理模型实验成像结果

4.3.2 3 种参考电极模式下的目标体深度信息提取结果

在EIS 有效检测深度范围内，本实验按照表1所示的目标体深度位置获取EIS 检测数据，并基于实测数据对本算法的性能进行评价。由本文第3 章节中关于公式（7）中i'（x0，y0）、i'（a，b）、i（x0，y0）、i（a，b）参数的确定方法可知，参考电极位置（a，b）的选择方式是利用EIS 实测数据进行目标体深度信息求解的关键，为此通过物理模型实验研究，对3 种不同参考电极模式下计算得到的目标体深度信息估算结果进行分析。经多组数据测试后，按照目标体靠近检测电极、目标体逼近最大可探测深度以及目标体处于中间探测距离3 种情况对检测结果进行分类，实验部分分析结果如图7 及表1 所示。

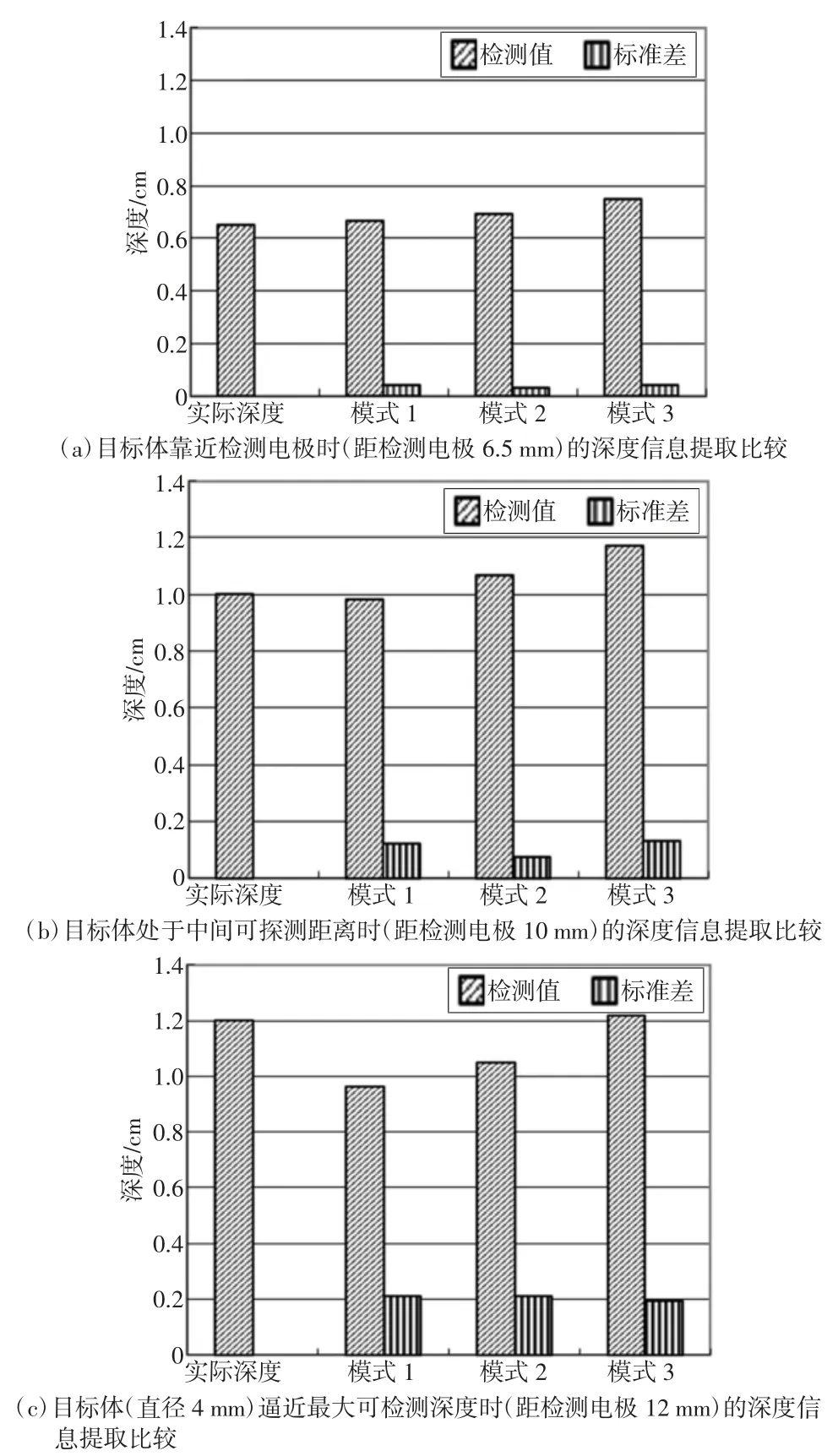
图7 目标体深度信息提取结果

表1 物理模型下真实深度值与近似计算值之间的差异（） 单位：cm

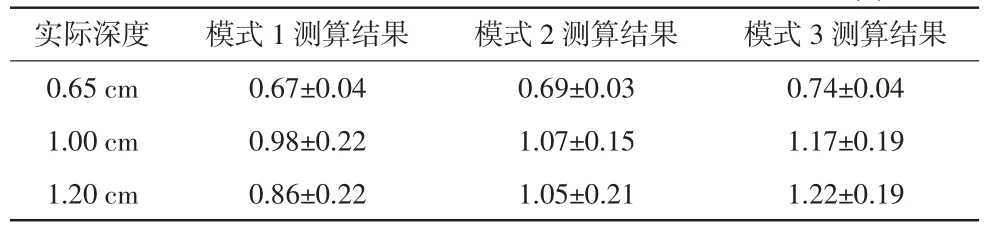
表1 物理模型下真实深度值与近似计算值之间的差异（） 单位：cm

实际深度0.65 cm 1.00 cm 1.20 cm模式1 测算结果 模式2 测算结果 模式3 测算结果0.67±0.04 0.69±0.03 0.74±0.04 0.98±0.22 1.07±0.15 1.17±0.19 0.86±0.22 1.05±0.21 1.22±0.19

为与仿真条件下的计算结果进行对比，按照物理模型的设置条件进行仿真模式设置，为了模拟实测条件对仿真结果添加1%的随机噪声后进行深度近似求解，结果见表2。

表2 仿真条件下真实深度值与近似计算值之间的差异（） 单位：cm

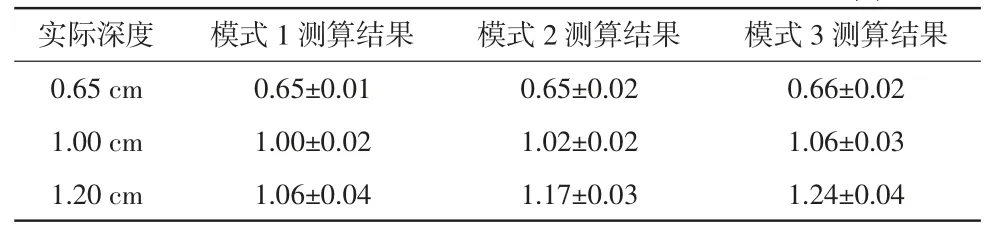
表2 仿真条件下真实深度值与近似计算值之间的差异（） 单位：cm

实际深度0.65 cm 1.00 cm 1.20 cm模式1 测算结果 模式2 测算结果 模式3 测算结果0.65±0.01 0.65±0.02 0.66±0.02 1.00±0.02 1.02±0.02 1.06±0.03 1.06±0.04 1.17±0.03 1.24±0.04

由图7 及表1、表2 显示结果，并结合多组实验数据分析可以得到：

（1）对比表1 和表2 可知，仿真条件下的深度预测准确性要高于物理模型实测条件下的结果，原因在于仿真条件下可以获得i0的真实值，而且仿真条件下可以避免实测环境下由测量系统、电极等引入的噪声。

（2）目标体未达到EIS 最大可探测深度前，3 种参考电极模式下所计算的目标体深度参数虽然各不相同，但深度计算参数均接近真实值。而当逼近EIS极限可检测深度时，3 种参考电极模式下所计算的目标体深度参数的标准差均升高。由此可见，在深度信息求解时，对目标体数据采集质量有较高要求，当目标深度增大时，EIS 对目标体的成像质量会变差。而测量数据是深度算法的数据来源，随着测量数据质量的下降，深度算法的准确性会降低。

（3）在其他条件相同的情况下，计算出来的深度参数均为模式1＜模式2＜模式3。在目标体所处实际深度较浅时（≤10 mm），利用参考电极模式1 得到的结果更加接近实际深度。当实际深度≥12 mm 时，参考电极模式3 的结果与实际深度更为接近。而参考电极模式2 的结果对浅目标和深目标的深度参数计算误差相对均衡。在本实验验证中，如果选择参考电极模式1，则该算法对深度为10 mm 内的目标体可准确提取其深度；而如果选择参考电极模式3，则该算法能够正确检测的最大深度会增加，但对近距离目标体深度计算时，模式3 相比模式1 其准确度有所下降。值得说明的是，本研究中的3 种电极参考模式实质代表3 种参考电流i（a，b）的选取方法。由此可见，本文中的深度信息求解方法的准确性与参考电流i（a，b）的选取方法相关性较大，在临床实际应用中，如何选择参考电流i（a，b）也将成为本文深度提取算法应用的关键。

5 结语

由于临床上单侧乳房通常不会出现多发性乳腺癌包块，所以在EIS 乳腺检测中研究者基本都是针对单目标体检测进行讨论，本文也是针对单目标体的深度提取方法开展相关研究。但是可以推测对多目标进行检测时，该方法还是有局限性的，算法的准确性应该与目标大小、目标之间的距离等有关。在乳腺EIS 研究中，对目标体深度信息提取是EIS 数据挖掘的重要工作。前期研究者虽然进行了相关探索工作，但深度提取算法多处于计算仿真阶段，尚无成熟应用于实测数据的方法。本研究首先利用乳腺EIS“双层球面模型”对目标体深度提取方法进行推导，进一步提出了用EIS 实测数据逼近深度求解的方法，并在物理模型实验中进行深度求解算法验证，实验结果证实了本文深度提取算法的可行性。虽然在深度求解中如何优化选择参考电流参数仍需进一步深入研究，但本研究可为乳腺EIS 检测中如何对癌包块进行立体信息定位提供解决思路，对进一步拓展EIS 临床应用具有积极作用。