基于实测数据与数理统计的高速公路车辆跟驰特性研究
朱凯舟,沈家军,王笑笑,周 倩
(扬州大学建筑科学与工程学院,江苏 扬州 225127)
1 引 言
随着中国经济的快速发展,人们对长距离出行及物流速度的要求越来越高,高速公路已经成为继航空、铁路运输之后中国又一运输大动脉,在国民经济中扮演着重要的角色。然而,相较于航空铁路,高速公路的行车安全问题并没有得到很好的解决。据有关部门统计,仅2016年我国高速公路总事故量就达到了惊人的8 934起,共造成5 947人死亡,11 956人受伤,这其中追尾事故达到了七成,成为高速公路行车安全的头号杀手。
目前关于高速公路的安全性研究主要集中于微观的驾驶人驾驶行为研究和宏观的交通流研究。吴玲等从驾驶员的驾驶熟练度方面研究了高速公路行车风险,阐述了基于安全车速差的驾驶人行为风险量化方法;陈岳峰等从驾驶行为和交通流两方面出发,构建了高速公路路标效用评价模型,从路标的角度提高高速公路行车安全;黄雪强从驾驶员的个体属性角度出发,通过调查问卷研究不同驾驶行为下的行车风险因素。事实上,当前的研究成果很少通过数据采集来探究高速公路的安全特性,多数都通过微观建模来研究本文结合交通领域的研究状况,鉴于追尾事故的高发性,从车辆跟驰的角度出发,采集扬州邗江槐泗段高速公路的行车数据进行统计分析,探究高速公路的车辆跟驰特性。
2 数据采集
为获得可靠行车数据,本文选取启扬高速242k+309B(瘦西湖东)一处位置对数据进行采集,如图1所示。本论文共采集得到4 503组数据,采集时间2019年6月1日上午8点到10点,下午2点到4点,共计4小时,天气情况良好。

图1 数据采集视频场景
3 调查方法
调查使用视侦通视频软件,通过获取车辆通过观测断面1和观测断面2的帧数来计算车辆的单车地点速度、车头时距、车间距、车长等信息,具体的计算公式如下所示。
(1)单车地点速度:车辆通过某一断面的速度。计算如式(1)所示
(1)
式中:vn(t)-t时刻n车的地点速度,单位m/s,其中n=1,2,3……;bn,1-n车车头在断面1处读取的图像帧数;bn,2-n车车头在断面2处读取的图像帧数,k=25帧/s,即每帧0.04 s;S-断面间距,本研究取S=30 m。
(2)车头时距:行驶于同一车道上的前车车头与后车车头经过同一断面的时间差。计算如式(2)所示
ti=(bi,1-bi-1,1)×k
(2)
式中:ti-i车的车头时距,单位s;bi,1-i车车头(后车)在断面1处读取的图像帧数;bi-1,1-i-1车车头(前车)在断面1处读取的图像帧数,k=25帧/s。
(3)车头间距:行驶于同一车道上的前车车头与后车车头之间的距离。计算如式(3)所示
hi=vi(t)×ti
(3)
式中:hi-i车(后车)与i-1车(前车)的车头间距,单位m;ti,vi(t)的含义如前所述。
(4)车间距:行驶于同一车道上的前车车尾与后车车头之间的距离。计算如式(4)所示
Hi=hi-bi-1
(4)
式中:Hi-i车(后车)与i-1车(前车)的车间距,单位m;bi-1-i-1车的车长(即前车车长),单位m;hi的含义如前所述。
(5)车身长度计算如式(5)所示
(5)
式中:bn-n车的车长,单位m,其中n=1,2,3……;b’n,1-n车车尾在断面1处读取的图像帧数;bn,1-n车车头在断面1处读取的图像帧数;vn(t)、k的含义如前所述。
(6)速度差:行驶于同一车道上的后车速度与前车速度之间的差值。计算如式(6)所示
Δv=vm-vm-1
(6)
式中:Δv-m车(后车)与m-1车(前车)的速度之差,单位m/s;vm、vm-1-后车速度、前车速度,单位m/s。
4 结果与讨论
4.1 车头时距分布规律
车头时距能够在时间上反映车辆跟驰的安全程度,车头时距越小,发生追尾的概率就越大,反之则越安全。根据目前交通领域关于车辆跟驰的理论,本文分车型、车道和跟车形式,选取车头时距不大于6 s的车辆样本作为跟驰车辆进行统计,统计结果见表1。
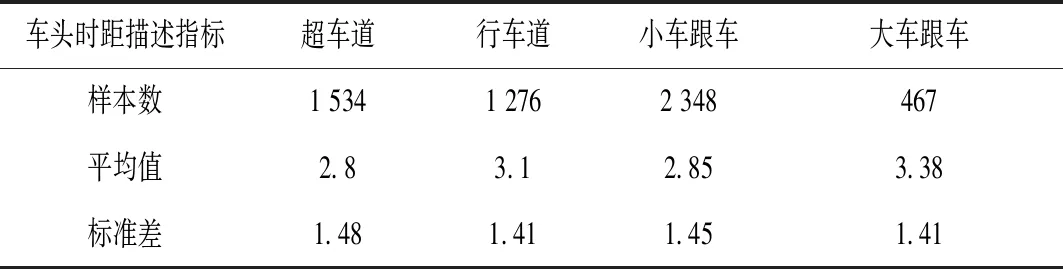
表1 不同车道、不同跟车形式的车头时距描述指标(s)
从以上数据可以看出,分跟车形式,小车跟车的平均车头时距小于大车跟车;分车道,超车道车辆的平均车头时距小于行车道车辆。究其原因,是因为超车道是供车辆超车和车辆速度达到较高水平的车辆行驶,前后车辆之间跟车较为紧密且车速较高,造成车头时距较行车道偏小,而大车由于制动水平低于小型机动车,为安全起见,大车司机普遍会和前车拉开较大距离并保持较低车速行驶,造成大车跟车的车头时距大于小车跟车。
4.2 跟车速度分析
作为车辆跟驰的要素之一,跟车速度对车辆跟驰的安全性影响巨大。跟驰车辆的速度越高,对驾驶员的反应要求也越高,由此产生的行车风险也越大。本文将车头时距不大于6 s的车辆判定为跟驰状态,统计分析车辆的跟驰速度,结果如图2、表2所示。
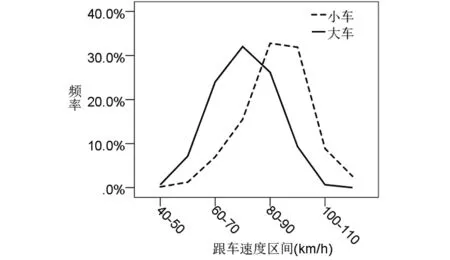
图2 不同跟车形式行驶速度频率图
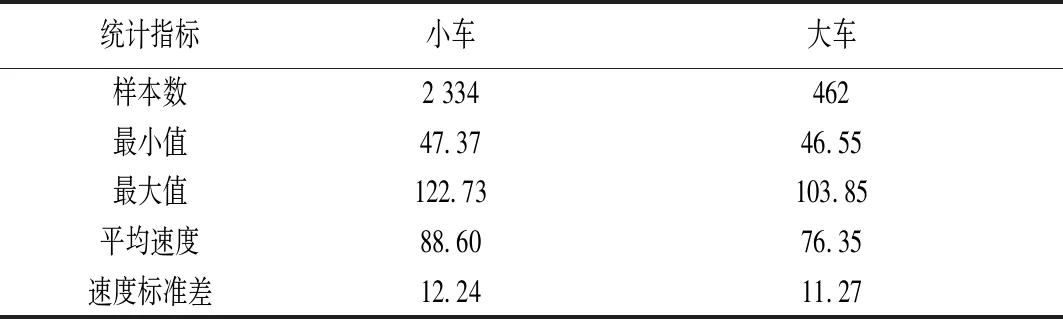
表2 不同跟车形式速度统计指标(km/h)
从以上图表信息可以看出,小车速度的最小值和最大值以及平均速度均超过大车,速度分布较大车离散,并且小车的高频率速度集中在80~100 km/h,而大车的高频率速度集中在60~80 km/h,究其原因,小车的制动性能更加优良,机动性较好,对环境的适应性比较高,司机驾驶较大车更加随心所欲,速度普遍较快,加大了车速的离散性,而大车由于自身车辆性能约束,为安全起见,司机普遍驾驶速度较低,更为谨慎,车速离散程度较小车比较小。
4.3 跟车车速差分析
后车与前车车辆的车速差大小是影响行车风险大小的因素之一,后车比前车越快,行车风险就越高。本文对车头时距小于6 s的跟驰车辆进行数据研究,研究结果如下图3所示。

图3 不同跟车形式车速差频率图
从上图数据可以看出,两种跟车车型的车速差主要集中于0附近,并且随着车速差绝对值的扩大,频率折线迅速下降,说明高速公路上面大多数跟车车辆速度较为均一,交通流运行比较流畅;在两种车型比较方面,大车跟车车型车速差小于0的比例大于小车,而在车速差大于0时,小车跟车的比例比大车高,究其原因,与前文分析内容一样,大车由于车辆性能较差,为安全起见,司机普遍会和前车保持安全距离,车速较低,造成后车比前车车速差小于0的比例比小车高。
4.4 跟车车间距分析
高速公路上机动车都处于高速运行状态,车间距的大小对行车安全影响巨大。本文基于跟驰车辆组的统计数据做了车间距研究,结果显示,大型车辆的跟车距离较小型车来说普遍更高。具体地,在0~50 m的距离范围内,小车的样本频率明显高于大车,而在大于50 m的跟车范围内,大车频率明显占上风,究其原因,是因为大车的操控性能,尤其是制动性能要比小车差很多,在同样的反应时间下大车的制动距离比小车高出许多,因此大车司机为了行车安全普遍会和前车拉开距离,采取稳健保守的驾驶行为。

图4 不同车型跟车间距频率分布图
4.5 后车车速与车间距分析
单一的交通流指标并不能全面描述车辆的跟驰特性,例如虽然后车的速度比前车大得多,但只要保持好一定的安全距离,车辆的行驶就仍然是安全的。为此,本文选取跟驰车辆样本,对后车的车速与车间距进行分析,结果发现跟车速度、跟车距离与各速度区间的的方差齐性检验的P值均小于显著性水平0.05,说明各个速度区间的跟车速度或跟车距离的方差存在显著性差异。通过分析各速度区间的标准差、四分位间距,发现随着速度的增大,跟车速度的离散性逐步减小,速度趋于集中,但前后车跟车距离的离散性在逐步加大,跟车距离的分布趋于分散。分析其原因,是因为在高速上随着车辆速度的提高,驾驶员变速的意愿逐渐降低,从而行车速度越大,分布越集中;与此同时,车速的提升也让驾驶员对前后车的距离更加敏感,为保持行车安全,驾驶员普遍会加大前后车距离,获得更大的自由行驶间距,这就提高了前后车车间距分布的离散性。

表3 不同速度水平下的跟车速度、跟车距离方差齐性检验表
4.6 车间距与车速差分析
在跟驰状态下,前后车的车速差会随着车间距的变化而发生动态变化,为研究这种变化的的分布规律,本文将速度差分为Δv>0(v后>v前)和Δv≤0(v后≤v前)两类,并以10 m为间隔对车间距进行分类,研究结果见图5所示。
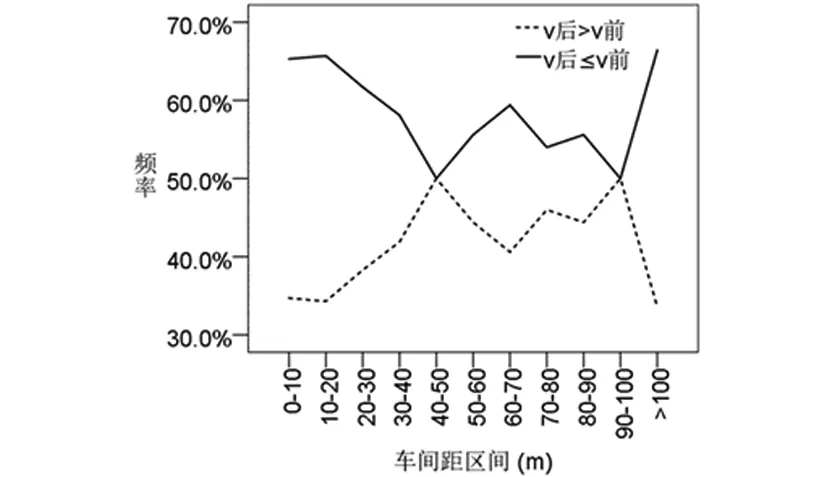
图5 不同跟车距离水平下两类车速差频率曲线
从以上数据可以看出,在车间距不大于50 m时,随着车间距的加大,后车车速比前车大的频率越来越高,当车间距在50 m到100 m时,两类车速差均呈现一定的波动性,当车间距大于100 m时,后车车速比前车慢的频率呈现陡升性。分析其原因,是因为当车间小于50 m时,随着车间距的加大,前车对后车的制约性得到了一定程度的减小,后车加速的意愿较为强烈,后车速度比前车大的频率也开始提高;当车间距在50~100 m时,前后车的制约程度达到了一个临界点,前车对后车的制约程度较低,此时后车速度受到前车车速、驾驶员行驶状态等多重因素的影响,频率曲线呈现一定的的波动性;当车间距大于100 m时,前后车已经足够安全,后车的加速意愿很低,加上高速上的限速因素,后车速度普遍比前车来得低,造成了频率曲线的的陡直。
4.7 后车车速与车头时距分析
在一般的跟车过程中,后车车速与车头时距紧密相关,本文选取符合条件的跟驰车辆样本,探究后车车速与车头时距之间的关系。研究发现当后车速大于90 km/h时,车头时距明显增大,但方差齐性检验的P值0.06>0.05,说明各个速度区间的车头时距方差并无显著性差异,同时平均值与5%截尾均值之间差异不大,说明数据并没有极端值或者极端值的影响被抵消得较为理想。分析其原因,是因为当后车速度较大时,后车对前车的注意性得到了提高,为安全起见后车普遍会控制速度,拉开与前车距离。而当跟车速度较小时,后车对前车的注意性被减弱,缩短了跟车距离,车头时距减小。

表4 不同跟车速度水平下的车头时距方差齐性检验表
4.8 车头时距与车速差分析
高速公路车辆在跟驰时,驾驶员通常都会选择合适的跟车距离,与前车保持一定范围的车速差,为此本文选取合适的车辆样本,以0.5 s为间隔划分车头时距间隔,研究了车头时距与车速差之间的关系,结果显示,当车头时距小于4.5 s时,两类车速差曲线波动较大,当车头时距大于4.5 s时,两类速度曲线较为接近和平稳,趋于频率50%。分析其原因,是因为当车头时距较小时,前后车在距离上普遍较为接近,增大了碰撞的风险,尤其当车头时距小于1 s时,后车车速较前车低的频率更是超过了70%;当车头时距大于4.5 s时,前后车普遍已经拉开较为安全的距离,两类车速差的频率分布差异逐渐缩小并趋于50%,符合实际驾驶的情况。

图6 不同车头时距水平下两类车速差频率曲线
5 结 论
为探究高速公路车辆的跟驰特性,论文结合启扬高速采集的实测数据,从数理统计的角度探究车辆跟驰的特点规律,主要结论如下:
(1)车头时距的分布受到车型和车道的影响,统计结果显示,分车道形式,超车道的车头时距平均值比行车道来得小;分跟车形式,小车跟车的车头时距比大车跟车来得小。
(2)大车和小车的跟车速度及跟车速度差存在一定的差异。统计结果显示,小车的跟车速度较大车来得大且离散,但在车速差方面两者均集中于0 km/h,并且大车跟车更偏向于行驶车速比前车小,同前车拉开比小车跟车更大的距离,同时,随着速度的增大,跟车速度的离散性逐步减小,速度趋于集中,但前后车跟车距离的离散性在逐步加大,跟车距离的分布趋于离散。
(3)车间距与车速差方面,当车间距介于50~100 m时,两类车速差频率均呈波动性;当车间距小于50 m时,两类曲线呈相交趋势;当车间距大于100 m时,两类速度曲线呈相离趋势。
(4)后车车速与车头时距方面,当后车速大于90 km/h时,前后车的车头时距明显增大,但各个跟车速度区间的车头时距方差并没有表现出显著性差异,车头时距的离散程度较为均一。
(5)车头时距与车速差方面,车头时距4.5 s是一个分界点,当车头时距小于4.5 s时,两类车速差曲线波动较大,当车头时距大于4.5 s时,两类速度差曲线较为接近和平稳,趋于频率50%。

