次品率对闭环供应链的影响分析和优化决策研究

葛祥龙，史成东 （山东理工大学 管理学院，山东 淄博255000）

0 引言

随着国家质量强国战略出台，中美贸易冲突的加剧，社会矛盾的转移，消费者对产品质量需求的提升，产品质量已经引起了供应链成员的密切关注。若产品的质量存在问题，不仅对供应链造成巨大的经济损失，也会损害公司的名誉。例如：2010年强生因污染和商标出错等原因召回40多种药物，公司销售额同比降低6亿美金；2016年三星因电池质量问题召回Galaxy Note7，企业在接下来两个季度损失接近30亿美元[1]。产品因质量问题而产生的退货行为时有发生，例如：福布斯对40家企业调查研究显示，产品的在线销售退货率高达30%[2]。由于机械、人工等客观因素，次品往往难以避免，崔铁军等[3]研究发现在流水线上的操作人员往往由于工作时间长而产生疲劳，导致生产的残次品增多，根据次品率统计，在8h内10个工人的次品率在0～0.2。公司为了预防产品因质量问题而造成的不良影响，也会做出应对措施，例如2019年长三角48家企业，其中包括银泰百货、联华华商、吉利汽车等，向社会公开承诺自愿参加长三角企业无理由退换货行动。

在现实情况中，由于产品的某些性质，若采取100%的质量全检，会丧失产品的实用价值，因此全检对于某些产品是行不通的，故只能采取抽样检验[4]。然而抽样检验势必会造成某些漏网之鱼，即次品的存在。Baiman S等[5]建立了供应商—销售商二级开环供应链，由供应商提供产品，销售商检测产品质量，文章对产品质量和检查精准度均衡进行了研究。Starbird S A[6]同样建立的二级开环供应链中除分析了销售商检测产品质量外，还制定了与产品质量相关的惩罚措施。但是Baiman S和Starbird S A的研究均假设产品质量在检测时没出现错误，然而在实际情况中质量检测错误时有发生，例如销售商会将次品通过检测，从而次品获得进入市场的资格。学者对于质检错误也进行了深入研究，Khan M等[7]在考虑产品质量检查错误的条件下，研究了有质量缺陷供应链的经济订货批量模型（Economic Order Quantity，EOQ）。Lee H H和Li C[8]也考虑产品质量检查错误的情况下，对比分析了激励、合作和检查对于供应商质量改进的效率。

依据以上研究，发现次品在供应链中存在是较为普遍的现象，但学者在研究闭环供应链的优化决策中为简化模型设计往往忽略次品因素，例如Savaskan R C等[9]研究了制造商回收、销售商回收、第三方物流回收的三种渠道产品再生产闭环供应链，陈菊红等[10]通过设计契约协调模型，实现了Stackelberg再制造闭环供应链系统的协调。李芳等[11]在研究有政府奖惩规制下的双渠道闭环供应链契约协调中，发现收益、费用共享协调决策是占优决策。也有学者意识到次品对于供应链的重大影响，但未分析次品率对于企业间优化决策的影响，例如Lee C H等[12]在销售商不完美的质量检验条件下，考虑次品存在于制造商、销售商二级开环供应链，分析了回购契约和收益共享契约对供应链的绩效表现。阮平等[13]研究了次品率对供应链的生产速率和生产成本的影响，徐兵等[14]研究了次品存在的单生产商和单销售商传统渠道供应链定货与信息服务的分散式与集中式决策模型，研究表明次品率的降低有利于供应链各企业的收益。Giri B C等[15]建立了在供应商、制造商、销售商和废旧产品收集者的闭环串行供应链中考虑次品存在的数学模型，并通过顺序和全局优化算法的研究表明供应链成员之间的整合可以提升总体利润。

结合以上文献研究，本文考虑销售商采取抽样检测的方式对单周期产品进行质量检测，抽样检测可能存在不完美检测的结果，故次品得以在制造商、销售商、消费者中流通，并以文献[10]模型为基础加入次品率这一因素进行延伸研究。

综上：依据以上文献研究结果表明，次品率的存在对于企业效益、企业形象的影响都是巨大的，然而由于产品的特性和不完美检测的存在，次品往往会流通至市场当中。而当学者研究企业收益占优决策时，为简化模型，往往会忽略次品这一重要因素。基于以上分析，本文建立有次品率存在的闭环供应链模型，分析次品率对于闭环供应链的产品批发价格、产品销售价格、企业收益和企业间优化决策的影响。

1 符号含义、模型基本假设、闭环供应链产品流动图

符号含义说明（如表1所示）。

表1 符号含义说明表

模型基本假设：

假设1：闭环供应链中只存在一个制造商、一个销售商和一个第三方回收商，以制造商为驱动下，进行产品的制造、销售和次品、废旧产品的回收再造。

假设2：闭环供应链博弈模型建立在有次品存在的产品单周期背景下，次品的存在由于产品质检的方式（抽样检验）和不完美检测造成。

假设3：废旧产品与次品可以再制造，再造产品单位成本均以cr计算，再造产品的品质与新鲜原材料制造的相同。再制造节约的单位产品成本为Δ，Δ=cm-cr，cm＞cr。

假设4：以谁生产谁负责的原则，返还的次品全部以原价、原路径退回。

假设5：为简化模型计算，产品、次品、废旧产品的仓储、运输成本均考虑在相应的价格中。

假设6：市场需求只与产品销售价格有关，市场需求函数为：D （p）=α-βp，其中α为市场基本需求，β为消费者对销售价格的敏感系数，α＞0,β＞0。

假设7：废旧产品回收总量G （b3p）=k+hb3p，k是消费者无偿返还废旧产品的数量，k越高，代表消费者环保意识越高，h是消费者对于回收价格的敏感系数，k＞0，h＞0。

假设8：回收成本Cb（b3p）=lG （b3p）2，l与产品的回收特性有关，l越大产品回收越困难，l＞0。

假设9：制造商、销售商、第三方回收商之间信息共享。

闭环供应链产品流动图（如图1所示）。

制造商以批发价格w将产品批发给销售商，销售商以销售价格p将产品销售给消费者，若消费者购买产品后发现次品，将次品以销售价格p退给销售商，销售商将次品以批发价格w返还给制造商；第三方回收商以回收价格回收废旧产品，将废旧产品以出售价格卖给制造商。闭环供应链以此形成了产品的正向物流、次品和废旧产品的逆向物流。

2 分散决策

闭环供应链各企业在分散决策下，均考虑自身收益最大化，企业间的决策互不影响。销售商、第三方回收商和制造商的最优收益函数如下：

分析销售商和第三方回收商的收益模型，求导销售价格p、回收价格b3p，得销售商和第三方回收商获最优收益时的销售价格和回收价格，如下：

将式（2）带入制造商的收益模型中。分析带入后的模型，求导批发价格w、废旧产品的出售价格bm，得制造商获最优收益时的批发价格和废旧产品出售价格，如下：

将式（3）与式（2）整合，得简式，如下：

定理1：次品率λ与批发价格wd、销售价格pd呈正相关关系，且批发价格wd相较于销售价格pd对次品率λ的变化更加敏感。

证明1：依据式（4），将wd、pd对λ求导，得：在λ⊆［0,1］的区间内：，且

经计算得供应链各企业的最优收益表达式，如下：

3 集中决策

集中决策下制造商、销售商和第三方回收商作为整体来进行产品的制造、销售和次品、废旧产品的回收再造，以期获得系统收益最大化，系统收益模型如下：

分析系统收益模型，对销售价格p、回收价格b3p求导，得：

定理2：次品率λ与销售价格pc呈正相关关系。

证明2：根据式（7），将pc对λ求导，得：dpc/dλ=cr/2（ 1- λ）2，在λ⊆［0,1］的区间内（dpc/dλ）＞0。将式（7）带入式（6）中，即得集中决策下系统最优收益表达式，如下：

结论1：分散决策下闭环供应链各企业均考虑自身收益最大化，导致了产品正向流动，废旧产品逆向流动中的双重加价效应，即：。此现象造成闭环供应链的内部消耗，故不能达到集中决策下的水准；相对于集中决策，分散决策下更高的销售价格减少了市场需求，低廉的回收价格提高了废旧产品回收的难度，产品、废旧产品的价格直接影响消费者的消费力度、废旧产品回收的参与度。

考虑产品同质，与集中决策相对比，分散决策下的闭环供应链未达到最优状态，然而集中决策在实际情况中难以实现，故本文通过契约协调（收益、费用共享）手段，对闭环供应链进行优化。

4 契约协调决策

契约协调决策打破了分散决策的弊端，闭环供应链各企业更多考虑如何减少企业间消耗，达到集中决策时的状态。故闭环供应链各企业以集中决策下销售价格、回收价格和系统收益为标杆进行收益与成本的分享。制造商作为闭环供应链的驱动者和契约协调的角色，分享销售商的销售收益同时承担第三方回收商的回收成本，分别为φ1、φ2为分享收益、承担成本的比例，其范围初定为［0,1］。

根据以上分析，得契约协调决策下销售商、第三方回收商和制造商的收益模型，如下：

为达成集中决策时的状态，将契约协调决策下销售价格、回收价格构建成与集中决策时一致的水平，如下：

令ps=pc，，得：

证明4：契约协调与集中决策次品率相同情况下，销售价格、回收价格达到了集中决策时的水平，这意味着市场需求、废旧产品回收总量也达到与集中决策时的水平。同时契约协调决策下的企业之间也达成了协调（式（11）），故契约协调达成了集中决策时的系统收益。

依据式（7）、式（8）、式（11）得出销售商、第三方回收商和制造商的最优收益表达式，如下：

定理5：企业若实施契约协调决策，必须满足以下φ1、φ2的范围，为：

证明5：契约协调达成的前提：制造商、销售商、第三方回收商在契约协调决策下比分散决策下收益更高。故将分散决策、契约协调决策下闭环供应链参与者的最优收益表达式各自进行对比计算（对比式（5）、式（12）），即得φ1、φ2的取值范围。

结论2：有次品存在的闭环供应链通过契约协调的方式达成了集中决策时的系统收益水平，若定理5成立，则销售商、第三方回收商、制造商均可获取更优收益；对于闭环供应链外部，更低的销售价格、更高的回收价格无疑是增大了市场需求和消费者对废旧产品回收的支持。

5 算例仿真与灵敏度分析

为验证以上分析的结果和观察次品率对契约协调决策、企业收益、批发价格、销售价格的影响，假定闭环供应链参数为：

契约协调决策顺利实施条件下，次品率λ的变化范围。

依据以上参数设置和定理5，可以确定契约协调决策时的收益分享比例φ1随次品率变化曲线，如图2所示。

由图2曲线变化趋势和定理5的分析，可得当次品率超过0.25时，契约协调在闭环供应链中无法实现，因为此时销售商在契约协调决策下的收益低于分散决策时的收益，销售商以收益角度无法接受契约协调决策。

确定次品率为0.1，在不确定的协调比例下，契约协调与分散决策时闭环供应链各企业的参数对比。

当确定次品率为0.1时，通过定理5，计算得收益分享比例变化范围：φ⊆［0.2 5,0.43］，如图3。

闭环供应链其他参数计算结果见表2。

表2 次品率确定，闭环供应链参数变量计算结果

为更清晰观察在次品率恒定（λ= 0.1）的状态下，闭环供应链中各企业采取契约协调决策随收益分享φ1、费用承担φ2比例变化的收益曲线，如图4至图6所示。

确定次品率λ=0.1，闭环供应链各企业为实施契约协调决策从而获得更优收益，可得收益分享比例φ1⊆［0．2 5,0．43］，费用承担比例φ2⊆［0.2 5,0.5］，结合表1和图4、图5、图6，得：

（1）闭环供应链各企业通过契约协调决策，降低了批发价格、销售价格、废旧产品出售价格，提高了回收价格，减少了闭环供应链的内部消耗，提高了市场需求。

（2）闭环供应链实施契约协调决策，销售商、第三方回收商、制造商的收益均比分散决策下的收益更高。

验证了结论1、结论2的有效性。

确定收益分享、费用承担比例均为0.32，契约协调与分散决策下闭环供应链各企业的收益对比。

当收益分享比例为0.32时，结合定理5，计算得次品率λ⊆［0,0.2］，如图7所示。

闭环供应链各企业收益计算结果见表3。

为更清晰观察在协调比例确定（φ1=0.32,φ2=0.32）的状态下，闭环供应链中各参数随次品率（λ⊆［0,0 .2］）变化的曲线，如图8至图10所示。

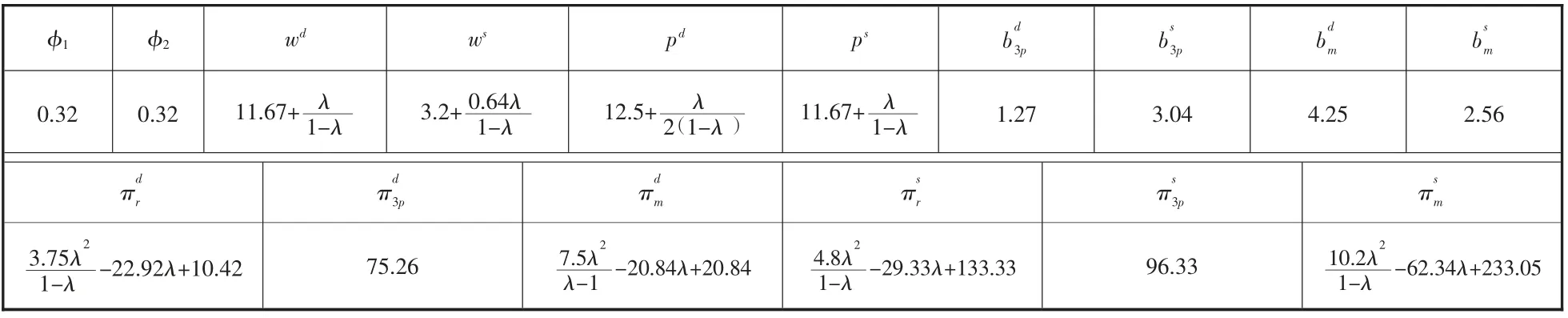
表3 协调比例确定，闭环供应链参数变量计算结果

在确定收益分享φ1、费用承担φ2比例均为0.32的状态下，经计算得企业间实施契约协调决策能够接受的次品率范围λ⊆［0,0 .2］，结合表2和图8、图9、图10可得：

（1）批发价格、销售价格与次品率呈正相关关系；且在契约协调决策下，闭环供应链成员拥有更低的批发价格、销售价格、废旧产品出售价格，更高的回收价格。

（2）销售商、第三方回收商、制造商在契约协调决策下获取了更优收益。

（3）销售商、制造商在契约协调决策下，随次品率的增加企业的收益均随之降低。

验证了定理1、2、3的有效性。

6 总结

本文以Stackelberg博弈模型为基础，以企业效益最大化为准则，考虑次品对闭环供应链中产品批发价格、产品销售价格、企业收益、企业间决策的影响，以期为闭环供应链各企业提供一些决策建议，主要结论如下：

（1）契约协调决策是闭环供应链各企业在考虑效益最大化的占优决策，通过实施契约协调决策，能够降低闭环供应链成员间的内部消耗、提高市场需求和消费者对废旧产品回收的支持。

（2）次品率的大小会影响契约协调决策能否在闭环供应链中顺利实施。当次品率超过一定限度时，销售商在自利动机驱使下，会采取分散决策保护自身效益。

（3）若次品率的范围在各企业能接受契约协调的前提下，产品的批发价格、销售价格与次品率呈正相关关系；制造商、销售商的收益与次品率呈负相关关系。

通过研究，可以得到如下决策启示：对于制造商而言，作为闭环供应链决策的驱动者和产品质量的把控者，为顺利实施契约协调决策，要严格把控产品质量，降低产品次品率。对于销售商而言，一是改进产品质量检验方式，减少质量检测时的出错率；二是可以通过以往周期产品的次品率来决定是否接受契约协调决策。