RS码的分布式编码协作系统方案设计

黄雅云

(南京航空航天大学 电子信息工程学院，江苏 南京 210000)

1959年，Reed和Solomon提出可以利用有限域中的多项式构造RS码(Reed-Solomon code)[1]。RS码的基础是循环码，可以用代数方法来构造和分析，因此可以找到多种实用的译码方法，且易于硬件实现。1961年Gorenstein等[2]发现RS码是BCH码(Bose,Ray-Chaudhuri,Hocquenghem Code)的一种子码，并提出了译码算法，但该算法在纠正大量错误时不够理想；1967年，Berlekamp[3]提出了Berlekamp-Massey译码算法，使得RS码能够纠正大量随机错误；1975年，Sugiyama等[4]证明欧几里得算法能够用于译码。现今RS码因具有强大的纠错性能，在无线通信、广播电视以及深空通信中有着广泛的应用[5]。

目前，RS码编码协作系统中使用的简单联合译码算法或智能联合译码算法，目的节点均不能充分利用获得的两路信号，误码率也不够理想。本文在参考前人文献资料的基础上，提出合并-智能联合译码算法。该算法能够充分利用获得的两路信号，进一步降低信噪比和误码率，提高RS码分布式编码协作系统的性能。

1 相关工作

1.1 信源与中继的相关编码

基于协作通信的三节点经典通信模型[6]，RS码编码协作场景的方案如图1所示。一个完整的编码协作传输流程，从信源产生信息到目的节点完整地译出信息，需要2个时隙[7]。在第1个时隙，信源首先将二进制序列m1映射为GF(2m)中符号序列a1，其中2m=n+1，n是码字长度；然后系统RS1(n,k1,d1)编码将符号序列a1编码，其中k1为信息位长度，d1为码字最小距离。由RS码的基础理论[8-9]可知，RS码的码字最小距离d1=n-k1+1。

RS1的生成多项式g1(x)由n-k1个根组成，g1(x)多项式可表示为：

g1(x)=(x-α)(x-α2)…(x-αn-k1)=

(1)

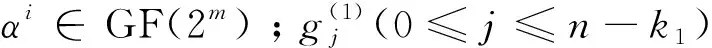
RS1码可以通过下式产生。

b(x)=a(x)g1(x)

(2)

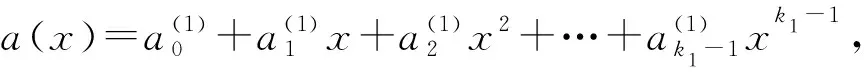
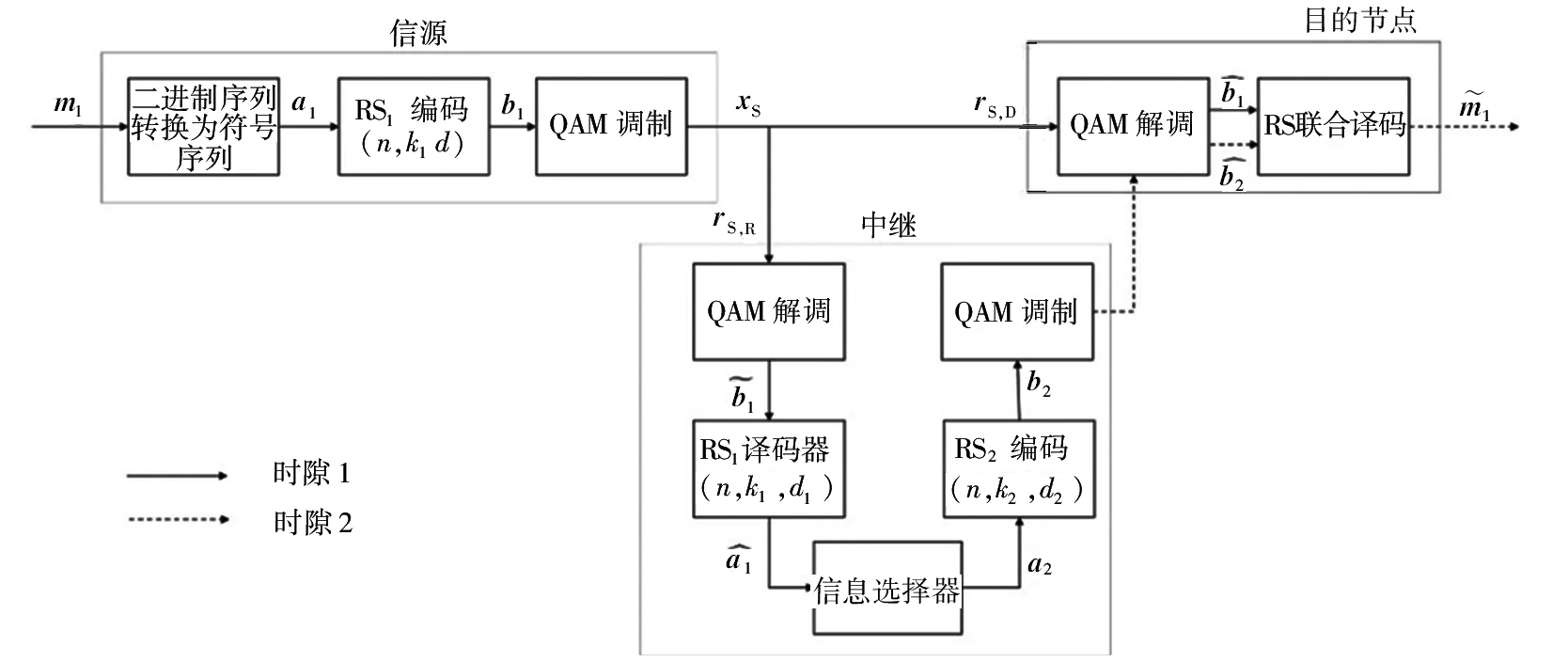
图1 RS码的编码协作系统框架结构Fig 1 Frame structure of RS code coding cooperation system

在编码协作方案中，使用系统RS码，其生成多项式可表示为：

b1(x)=xn-k1a1(x)+p1(x)

(3)

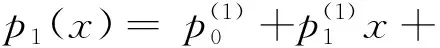
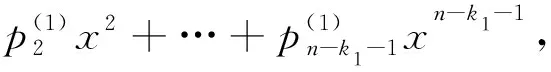
p1(x)可以通过GF(2m)中的多项式除法得到，计算式如下：

(4)

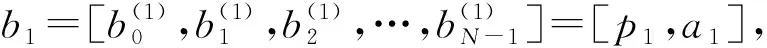
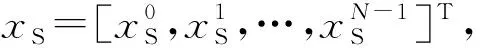
(5)

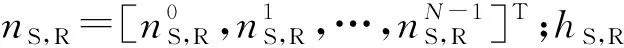
同样地，在第1个时隙，目的节点也将收到经信道传播的信息xS，令其为rS,D，表达式为：

(6)

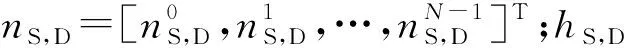
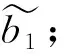
g2(x)=(x-α)(x-α2)…(x-αn-k2)=

(7)

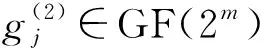
由于k1>k2，g2(x)比g1(x)有更多的根，所以RS2的纠错能力比RS1的高。系统RS2码可以表示为：

b2(x)=xn-k2a2(x)+p2(x)

(8)

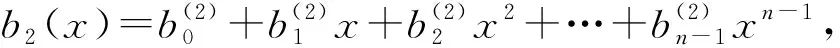
在此系统中，中继从信号

中选择前k2个符号作为信息a2。同样地，可以得到校验多项式p2(x),计算式如下：

(9)

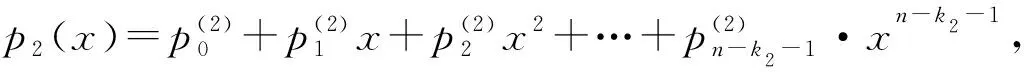
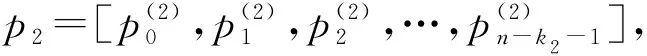
在第2个时隙，目的节点收到中继传输的信息rR,D，可表示为：

(10)

式中：hR,D是瑞利衰落系数，nR,D是高斯白噪声序列。

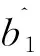
1.2 目的节点联合译码算法

联合译码是编码协作系统的关键特征之一，常用的联合译码算法有简单联合译码算法和智能联合译码算法。

1.2.1 简单联合译码算法

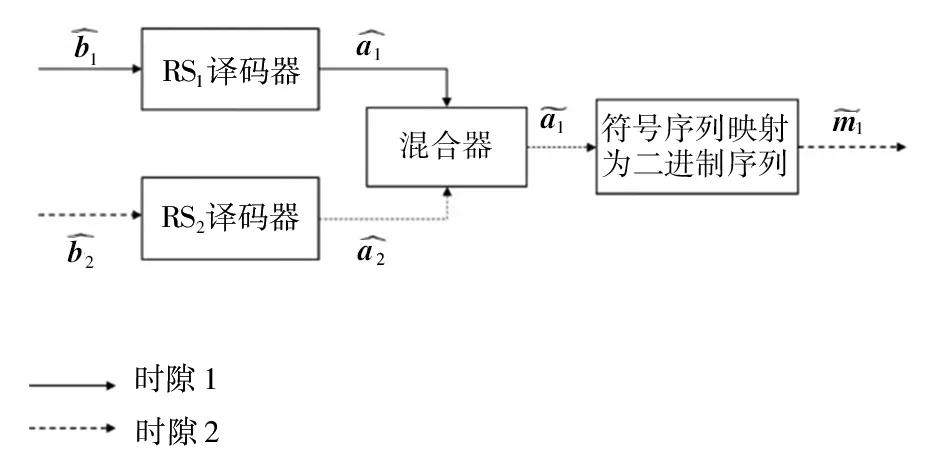
图2 简单联合译码算法框架Fig 2 Framework of simple joint decoding algorithm

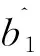
1.2.2 智能联合译码算法

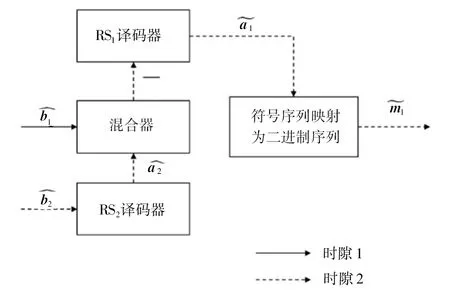
图3 智能联合译码算法原理Fig 3 Principle of intelligent joint decoding algorithm

1.3 两种联合译码算法的比较

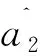
在智能联合译码算法中，不需要使用信噪比阈值来判断混合器的使用方式，而是使用RS2译码器的输出作为RS1译码器输入的一部分，因为RS2译码器可以纠正一部分传输错误，所以智能联合译码算法能够提高系统性能。但是在该联合译码算法中，目的节点仍旧不能充分利用获得的两路信号以降低系统误码率。

2 合并-智能联合译码算法设计

2.1 系统设计

为了目的节点能够充分利用获得的RS1和RS2两路信号，进一步降低系统误码率，提出了合并-智能联合译码算法，其具体框图如图4所示。

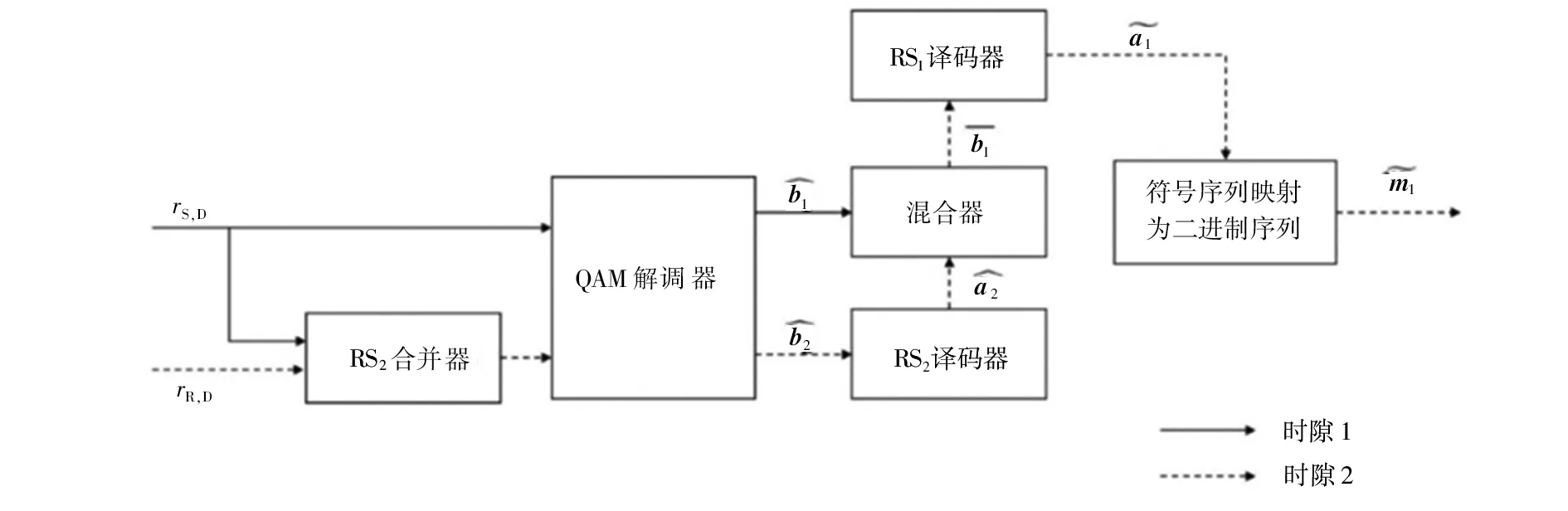
图4 合并-智能联合译码算法原理图Fig 4 Schematic diagram of merge-intelligent joint decoding algorithm

图4中，在目的节点的解调器之前增加一个合并器，将RS1的前k2个调制符号与RS2的k2个信息位的调制符号合并，合并系数参考协作通信中的最大比合并算法[12]。经过RS2合并器之后，调制序列为

(11)

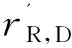
由此，系统可以充分利用RS1和RS2两路信号，使系统误码率进一步降低。

2.2 实现步骤

为实现上述算法，具体实现步骤如下：

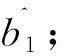
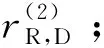
3 系统仿真及性能分析

在系统采用RS码的编码协作方案的基本框架时，分别对简单联合译码算法、智能联合译码算法与合并-智能联合译码算法3种不同的联合译码算法进行仿真实验，仿真条件如下：RS1码字为(63,51,13)RS码，RS2码字为(63,39,25)RS码，在AWGN信道中传输，使用64-QAM调制方式，设置信源—中继信道为理想信道，即σS-R=，且σR-D=σS-D+1。仿真结果如图5、图6。图5、图6中横坐标为信源—目的节点信道的信噪比，使用分贝数表示，单位为dB；纵坐标为误比特率(Bit Error Ratio，BER)。所示。需要注意的是使用合并-智能联合译码算法时，合并系数α随信噪比而变化。

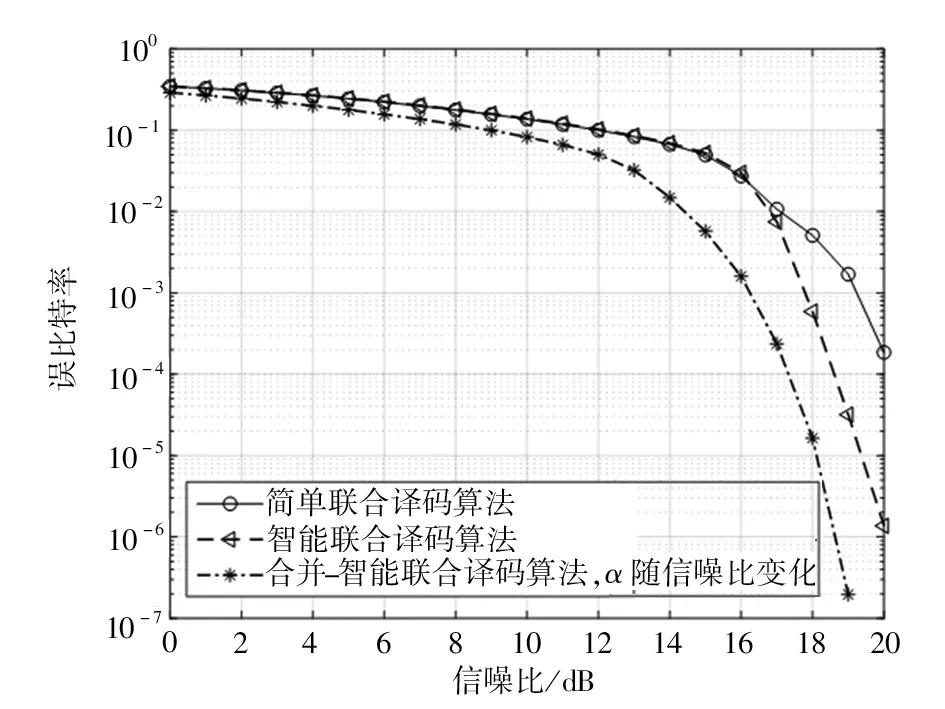
图5 不同联合译码算法的性能比较Fig 5 Performance comparison between different joint decoding algorithm

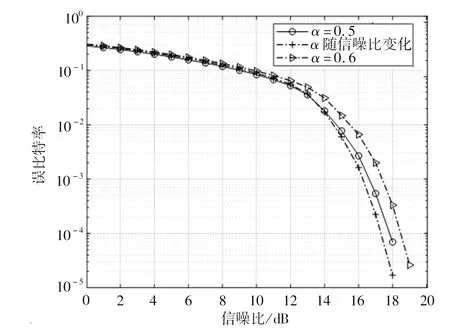
图6 合并-智能联合译码算法中使用不同合并系数的性能仿真Fig 6 Performance simulation of merge-intelligent joint decoding algorithm with different combining coefficients

图5为不同联合译码算法的性能仿真比较。从图5可以看出，当误比特率为10-3时，与非协作系统(non-coop)相比，使用简单联合译码算法的系统获得的增益只有0.6 dB，性能有限；使用智能译码算法的系统可以获得2.2 dB左右的增益；使用合并-智能译码算法的系统可以获得3.7 dB左右的增益。由此可见，使用合并-智能译码算法的系统误比特性能比使用智能译码算法的系统好。在低信噪比条件下，即当信噪比低于10 dB时，使用3种不同译码算法的系统误比特率性能相近；但当信噪比大于10 dB后，使用合并-智能译码算法的系统可以获得较大的性能提升。

图6给出了合并-智能联合译码算法中使用不同合并系数的性能仿真。从图6可以看出，当系统使用合并-智能联合译码算法时，不同的合并系数将会影响系统的性能，其中合并系数α随信噪比变化时，系统的性能会略好一些；当误比特率为10-4、合并系数为自适应系数时，系统性能比系数为0.5的好0.4 dB左右，比系数为0.6的好1 dB左右。

综上所述，合并-智能联合译码算法能够充分利用获得的两路信号，进一步降低信噪比和误码率，提高RS码的分布式编码协作系统的性能。

4 结语

本文分析了RS码的编码协作系统，研究了基于RS码的简单联合译码算法、智能联合译码算法。在此基础上，提出了合并-智能联合译码算法，并通过仿真比较了简单联合译码算法、智能联合译码算法与合并-智能联合译码算法3种不同的联合译码算法的性能。结果表明：合并-智能联合译码算法能够充分利用获得的两路信号，使其分集增益，进一步降低信噪比和误码率，提高RS码的分布式编码协作系统的性能。