GAMIT/GLOBK 多系统GNSS 数据处理分析
周建营,陈国恒,刘文建
(广东省国土资源测绘院,广州 510500)
0 引言
目前全球卫星导航系统(global navigation satellite system, GNSS)主要由美国全球定位系统(global positioning system, GPS)、中国北斗卫星导航系统(BeiDou navigation satellite system, BDS)、俄罗斯格洛纳斯卫星导航系统(global navigation satellite system, GLONASS)和欧盟伽利略卫星导航系统(Galileo satellite navigation system, Galileo)组成。随着这4 大系统的发展,精密定位服务也由单系统逐渐向多系统融合转变。多系统的组合定位能提供更多的可见卫星数和优化卫星的空间几何结构,以提高定位的精度[1]。对于GNSS 多系统在工程应用领域的数据处理研究,大多以GPS 作为主要的数据来源进行基线解算与平差计算,近年来不少学者利用国际 GNSS 服务组织(The International GNSS Services, IGS)观测站或连续运行参考站(continuously operating reference stations, CORS)的数据开始对BDS 数据进行精度分析。其中包括:文献[2]针对BDS 的相对定位问题,分析表明利用宽巷组合观测值进行BDS 基线解算是可行的,且与 GPS 精度相当;文献[3]利用GAMIT10.61 软件基于不同的参数对BDS 长基线精度进行分析,结果表明其解算的相对精度在1×10-8量级;文献[4]利用GAMIT10.61 软件对重庆8 个CORS 站的GPS 数据和BDS 数据进行处理,结果表明GPS 的解算结果整体优于BDS 的解算结果,但解算精度均能满足高精度的数据处理要求;文献[5]分别试验了利用GAMIT 软件进行BDS 的长、短基线解算,结果表明基于GAMIT 软件的BDS 精密定位解算精度较高;文献[6]通过GAMIT 软件对BDS 和GPS 的数据进行基线解算,结果表明GNSS 接收机收到的BDS 可见卫星的个数、分布和空间结构都不如GPS,导致BDS 的基线解算质量略低于GPS;文献[7]以国家GNSS 站的多系统观测数据作为研究对象,认为组合GPS/BDS 双系统解算能有效提升基线高程(U)方向的精度,而单BDS 基线解算精度尚不如GPS;文献[8]利用香港2017 年年积日第163—167 天的CORS 观测站进行GPS 和BDS 的数据处理,结果表明BDS 可应用于厘米级定位精度的测绘领域,但可用卫星个数不到GPS 的一半,导致卫星精密轨道和钟差精度相对较低;文献[9]利用新版GAMIT10.70软件解算GPS/BDS 基线,结果表明当基线较长时,GPS 基线解算精度和重复性均优于BDS 基线解算结果,当基线较短时,GPS 和BDS 的基线重复性均出现偏大现象。而对于GLONASS 和Galileo 的数据处理分析相对较少,其中包括:文献[10]利用我国和欧洲范围内的IGS 站GPS/GLONASS 观测数据,分析在Bernese 软件下,单系统和双系统定位结果的差异,结果表明GPS/GLONASS 组合定位比GPS 单系统的内符合精度要好,外符合精度在X、Y 方向上要好,在Z 方向上精度相当;文献[11]利用商用软件CGO 解算了BDS、GPS 和GLONASS 单星系统测量的GNSS 控制网,结果表明,GPS 的精度最高、BDS 次之、GLONASS 最差;文献[12]提出综合多系统组合的定位方法,同样采用商用软件CGO 处理GPS/GDS/ GLONASS 3 种组合的数据,结果表明GPS/BDS 方案较单GPS 或单BDS 可显著提高定位精度。
总体而言,在工程应用领域中,较少有利用GAMIT/GLOBK 软件进行GNSS 多系统高精度的数据处理分析。基于此,本文选择2019 年年积日第155—160 天香港CORS 的多系统观测数据,采用GAMIT/GLOBK10.7 软件分别进行单星基线解算,得到各系统的基线解算结果,再组合成多系统联合解进行平差计算,并对多系统数据处理精度进行分析,为GNSS 工程应用领域的高精度数据处理提供参考。但至截稿时,我国正在建设第3 代北斗卫星导航系统即北斗三号(BeiDou navigation satellite system with global coverage, BDS-3),暂未完成全球组网,只能利用北斗卫星导航(区域)系统即北斗二号(BeiDou navigation satellite(regional)system, BDS-2)的数据进行解算,因此本次实验采用的GNSS 卫星系统为GPS/BDS-2/GLONASS/ Galileo。
1 数据处理原理
1.1 基线解算原理
载波相位测量的观测值方程[13]为
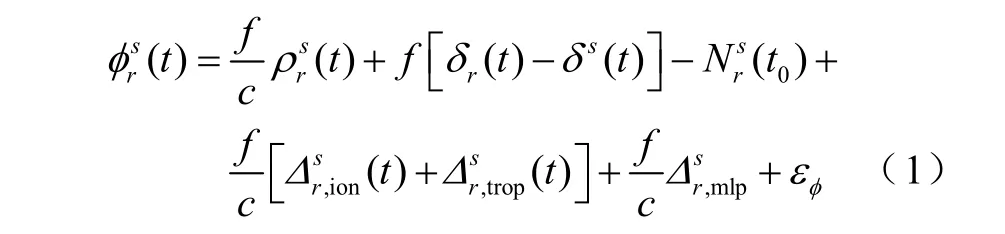
假设接收机A、B 同步观测s 卫星,由式(1)得到单差观测方程,并简化为
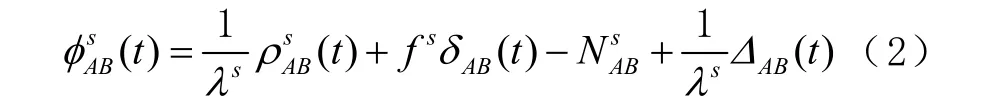
式中λ 为波长。由式(2)可见,单差法消去了卫星钟差。
假设接收机A、B 同步观测s、k 卫星(仅考 虑卫星频率相同,即 fs= fk),由式(2)可组成2 个单差观测方程,求差后得到双差观测方程,并简化为
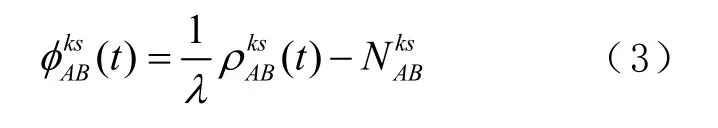
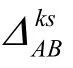
1.2 平差原理
GLOBK 平差采用的是卡尔曼(Kalman)滤波法,它将所有准观测值文件的松弛约束估计信息合并到1 个解中,并由时间更新和观测更新2 个步骤实现,其状态方程和观测方程为
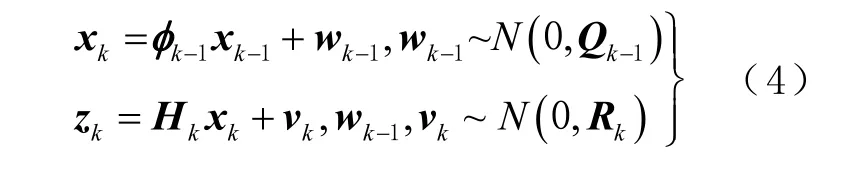
式中:x 和z 为状态和观测值向量;φ 为状态转移矩阵;H 为设计矩阵;w 和Q 为系统噪声向量及其协方差矩阵;v 和R 为观测噪声向量及其协方差矩阵。
时间更新,即卡尔曼滤波中的预报过程为
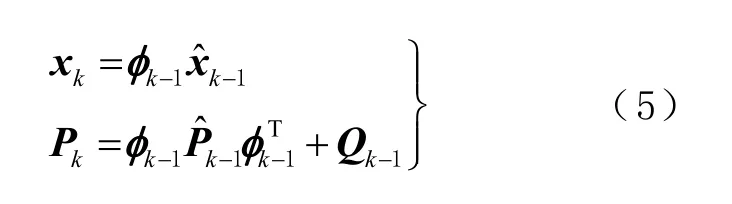
观测更新,即卡尔曼滤波中的改正过程为
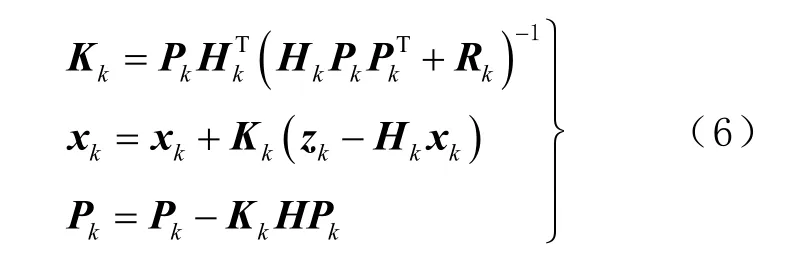
在GLOBK 软件中:上述公式变量x 为待估全局参数的解向量,初值为0,全局参数包括测站坐标及速度、卫星轨道参数等改正量;φ 为状态转移矩阵;P 为待估全局参数的协方差矩阵,其初值依据控制命令文件中的先验限制条件确定;Q 依据控制命令文件中马尔科夫(Markov)噪音项确定;H为待估全局参数的偏导数矩阵;R 为从准观测值文件中读取的协方差矩阵;z 为观测值和理论计算值的差值向量,其中观测值来自准观测值文件,理论计算值来自控制命令文件中的先验信息文件;下标表示输入顺序。
GLOBK 软件的平差原理可参阅参考文献[14-15]。
2 数据处理方案
本次试验数据采用 2019 年年积日第 155—160 天香港CORS 测站的多系统观测数据,分别是HKCL、HKKS、HKKT、HKLM、HKLT、HKMW、HKNP、HKOH、HKPC 共9 个测站。为保证各卫星系统解算参数保持一致,基线解算时的sittbl.表中测站约束设置HKKT 为0.05、0.05、0.05,其余测站均为100、100、100;历元间隔为30 s,卫星截至高度角为10°,海潮模型选择FES2004,其余参数均为默认;广播星历采用多模GNSS 实验跟踪网(multi-GNSS experiment, MGEX)[16]提供的混合星历产品,精密星历中BDS-2/GLONASS/ Galileo 采用武汉大学卫星导航定位技术研究中心( GNSS Research Center of Wuhan University, WHU)混合精密星历,由于使用WHS 混合精密星历解算GPS 过程中出现精密星历报错情况,故解算GPS 数据时,采用IGS 精密星历;在解算GLONASS 数据的过程中,出现5 号、9 号、17 号、21 号卫星不可用情况,故先剔除这几颗卫星再进行解算。各系统在基线解算批处理的命令为
1)GPS:sh_gamit-expt test -d 2019 155-orbit IGSF-gnss G -noftp;
2)BDS-2:sh_gamit-expt test-d 2019 155-orbit WUHM -gnss C -noftp;
3)GLONASS:sh_gamit-expt test -d 2019 155-orbit WUHM-gnss R-jclock sp3-noftp;
4)Galileo:sh_gamit-expt test-d 2019 155-orbit WUHM-gnss E-noftp。
基线解算后,分别得到各单星系统的o 文件、q 文件和h 文件,通过提取o 文件中的基线向量,比较年积日第155—160 天各系统的标准化均方差值(normalized root mean square, NRMS)值及基线固定误差和比例误差。而限于篇幅,选择提取年积日第 157 天的各基线分量,比较 GPS/BDS-2/ GLONASS/ Galileo 的基线解算精度。同样的,选择年积日第157 天的解算结果h 文件,以HKOH、HKKT、HKNP 作为固定约束进行GLOBK 平差计算,并生成单星及多星联合解进行平差精度的比较,平差方案为1)GPS;2)BDS-2;3)GLONASS;4)Galileo;5)GPS/BDS-2;6)GPS/GLONASS;7)GPS/Galileo;8)GPS/BDS-2/GLONASS/Galileo。
3 精度分析
3.1 基线解算结果分析
首先对年积日第155—160 天基线解算结果的NRMS值进行比较,它是用来表示单时段解算出的基线值偏离其加权平均值的程度[17],计算公式为
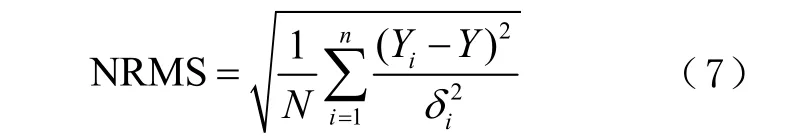
式中:N 为测站个数;iY 为年积日第i 天的基线边长;Y 为单天解基线边长的加权平均值;为单位权中误差。一般情况下小于0.3 即表示解算合格,其值越小证明解算质量越好。NRMS 值的比较分析如表1 所示。
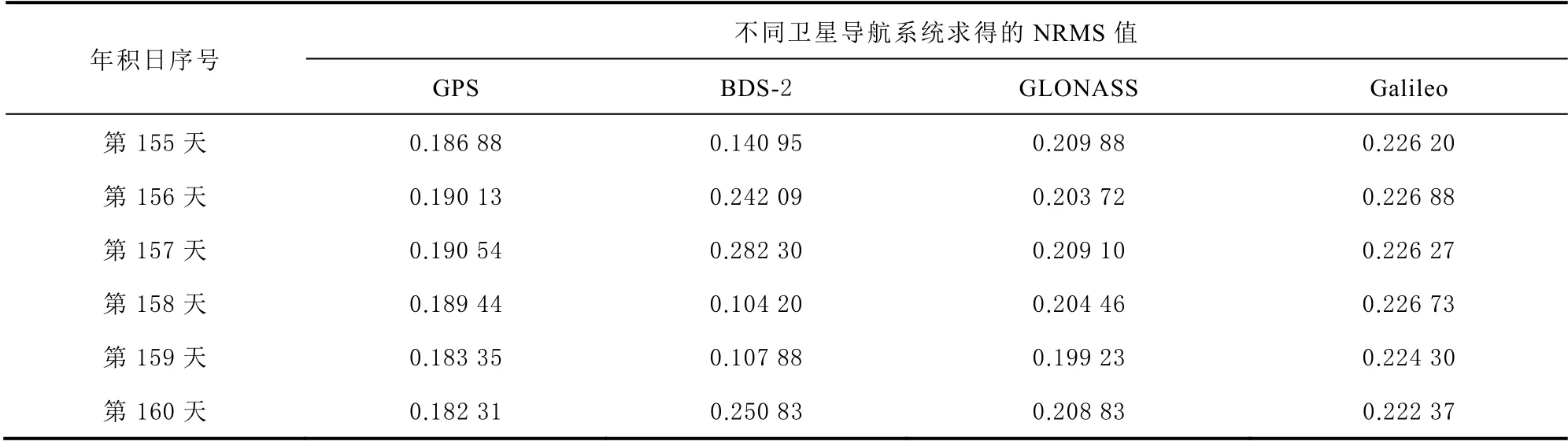
表1 各系统NRMS 值
由表1 各系统的NRMS值可得,GPS 均小于0.20,GLONASS 均小于0.21,Galileo 均小于0.23,而BDS-2 的NRMS值稍显不稳定,年积日第155 天、第158—159 天这3 d 小于0.15,年积日第156 天、第157 天、第160 天在0.24~0.29 之间,可能的原因是 BDS-2 精密轨道和钟差文件的精度要低于IGS 提供的 GPS 精密轨道和钟差文件[18-19],且GAMIT 软件使用的BDS 误差改正模型不够完善,误差消除不够彻底所导致[8]。但各系统的基线解算NRMS值均小于0.3,证明基线解算均良好。
再比较分析年积日第155—160 天的基线重复性,重复性定义[20]为
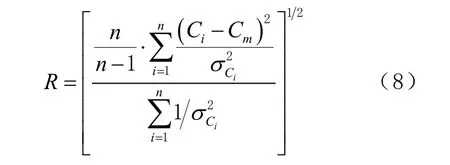
式中:n 为同1 基线的总观测时段数;Ci为1 个时段的基线某1 分量或边长;为该时段i 相应于Ci分量的方差; Cm为各时段的加权平均值。固定误差和比例误差如图1 所示。
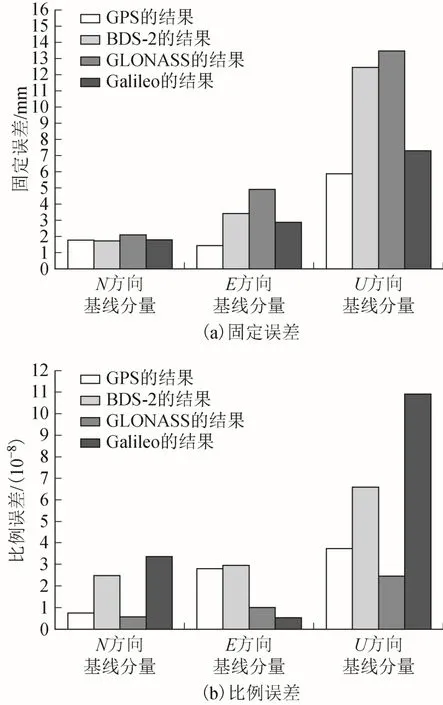
图1 年积日第155-160 天得的基线重复性
由图1 中年积日第155—160 天的基线重复性可见,在固定误差方面,各系统的N、E 方向均优于U 方向,其中N方向的固定误差精度相当,均小于2.1 mm;E 方向中,GPS 的误差最小,为1.45 mm;U 方向中,GPS 误差最小,为5.86 mm。在比例误差方面,N 方向 中,GLONASS 的误差最小,为0.557 55×10-8,E 方向中,Galileo 的误差最小,为0.527 96×10-8,U 方向中,GLONASS 的误差最小,为2.433 28×10-8。综合各系统的固定误差和比例误差分析而言,GPS 的基线重复性优于其他3 个系统。
为进一步分析各系统的基线解算精度,选取了年积日第157 天的解算结果进行比较分析,如图2 所示。
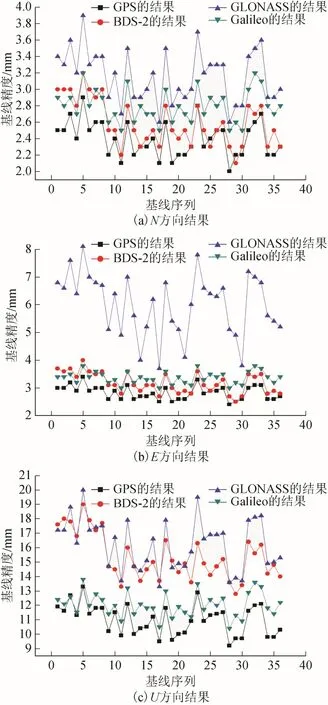
图2 各系统基线解算精度比较
由图2 各系统基线解算精度分析可得,在N 方向上,GPS 的解算精度最高,平均精度为2.39 mm,GLONASS 精度最低,平均精度为3.16 mm;在E方向上,GPS/BDS-2/Galileo 3 系统的解算精度相当,平均精度分别为2.83、3.18、3.37 mm,而GLONASS精度最低,平均精度为6.01 mm;在U 方向上,GPS的解算精度最高,平均精度为10.99 mm,Galileo 次之,平均精度为12.04 mm,而GLONASS 的精度最低,平均精度为16.22 mm。因此,在不同单星系统基线解算时,GPS 的基线解算精度依然最高。
3.2 平差计算结果分析
为进一步研究各系统的基线解算结果对平 差的精度影响,同样以选取的年积日第157 天解算结果h 文件为实验数据,利用GLOBK 软件分别进行各系统的平差计算。由于GPS 的基线解算精度最高,因此以GPS 作为组合基础,分别与BDS-2、GLONASS、Galileo 组成双系统联合解,同时组成GPS/BDS-2/GLONASS/Galileo 4 星多系统联合解算,分析不同方案的平差精度。比较分析结果如图3所示。
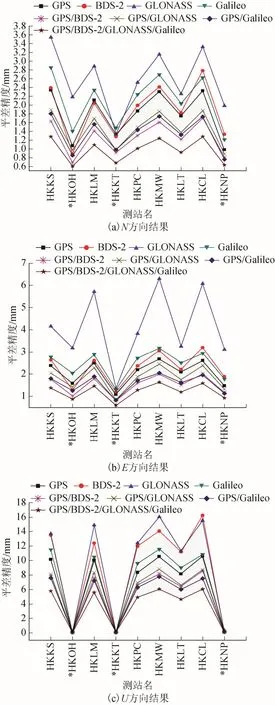
图3 多系统平差精度比较
由图3 多系统平差精度比较可得,若按单星解 进行的平差精度来看,在N、E、U 方向上的GPS平差精度均最高,平均精度分别为1.78、2.06、6.45 mm。若按双系统的平差精度来看,在N 方向上,GPS/BDS-2 的平差精度最高,相较于GPS 平均精度提高了29.97%;在E 方向上,GPS/BDS-2 的平差精度最高,相较于 GPS 平均精度提高了26.75%;在U 方向上,GPS/Galileo 的平差精度最高,相较于GPS 平均精度提高了26.62%。若按所有方案的平差精度来看,在N、E、U 方向上的GPS/BDS-2/GLONASS/Galileo 平差精度均最高,相较于GPS 平均精度分别提高了45.61%、41.23%、42.72%。
再通过平差结果中的坐标值进行分析,以平差精度最高的GPS/BDS-2/GLONASS/Galileo 平差坐标值作为基准,分别和其他方案的平差坐标值作较差,结果如表2 和表3 所示。
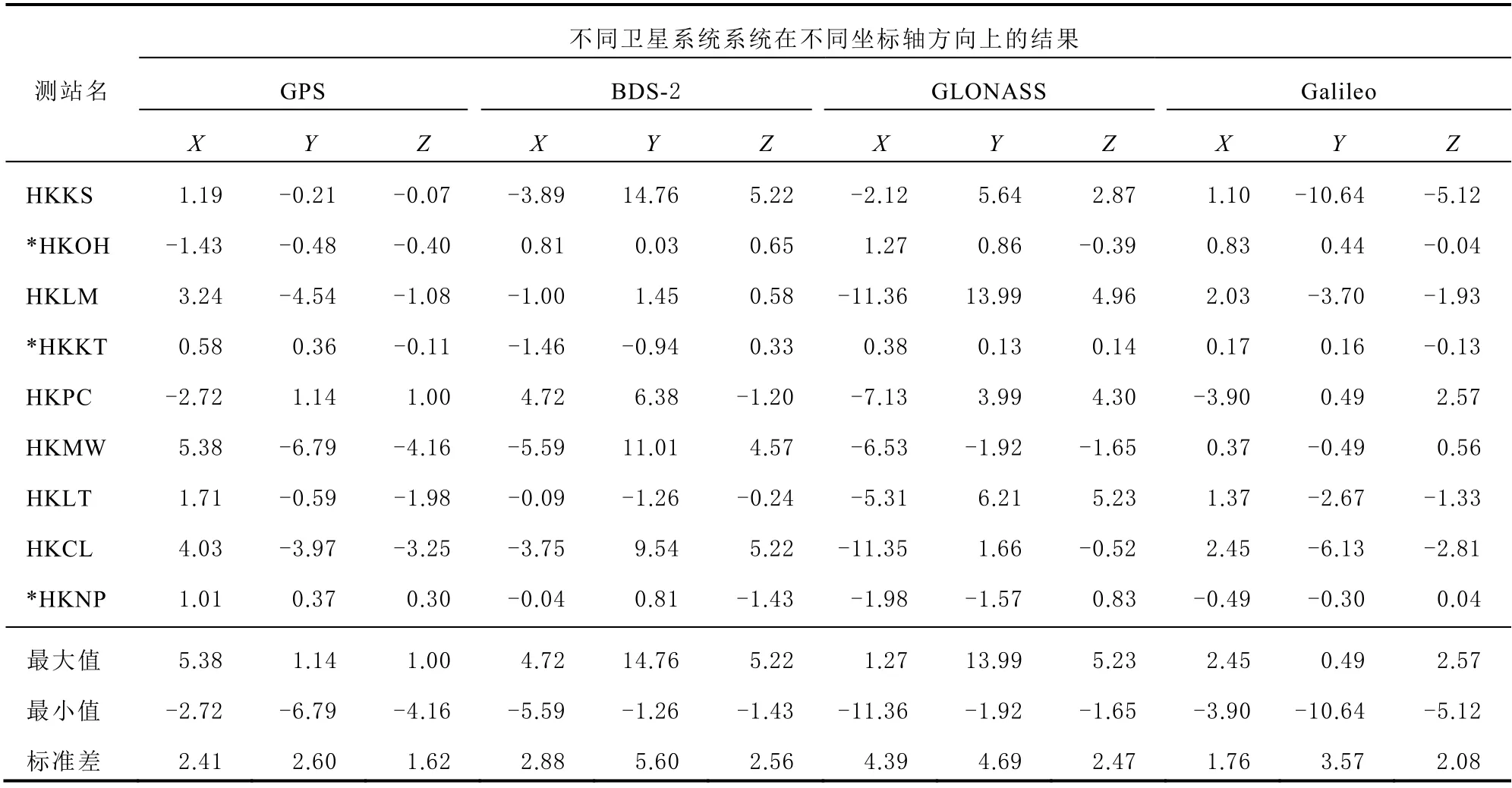
表2 与GPS/BDS-2/GLONASS/Galileo 坐标值较差比较 单位: mm
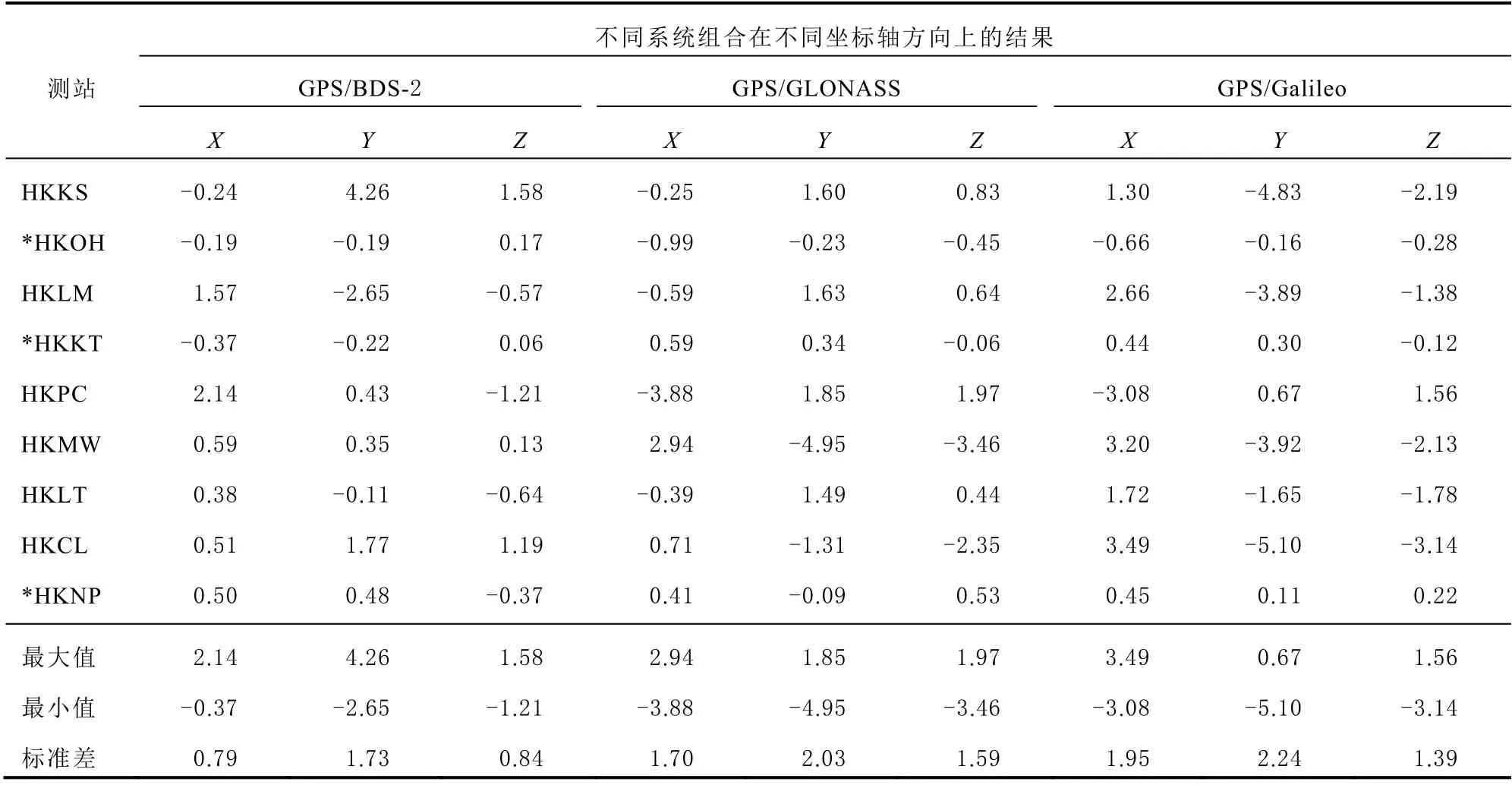
表3 与GPS/BDS-2/GLONASS/Galileo 坐标值较差比较 单位: mm
由表2 和表3 可得,当利用单星系统进行平差计算时,从较差的最大值、最小值及标准差来看,GPS 的坐标值和4 星系统最吻合。当利用双星系统进行平差计算时,从标准差来看,GPS/BDS-2 和4 星系统更接近,Y 方向的最大值为4.26 mm,最小值为-2.65 mm,较其他双系统稍大些,但均为毫米级的差异。
4 结束语
本文基于GAMIT/GLOBK10.7 软件进行GPS/ BDS-2/GLONASS/Galileo 多系统的基线解算及平差计算,得到以下几点结论:
1)通过年积日第155—160 天的基线解算,各个系统的NRMS 值均小于0.3,表明基线解算结果良好,但BDS-2 的这几天NRMS值稍显不稳定,年积日第155 天、第158—159 天这3 d 小于0.15,年积日第156 天、第157 天及第160 天则在0.24~0.29之间;重复性方面,综合固定误差和比例误差的比较,GPS 的基线重复性优于 BDS-2/GLONASS/ Galileo 3 系统。
2)选取了年积日第157 天的基线解算结果分析,在N、E、U 方向上,GPS 的基线解算精度最高,GLONASS 的基线解算精度最低,因此在单星系统基线解算上,GPS 是最优的选择。
3)选取了年积日第157 天的基线解算结果,分别进行单星系统及多星系统组合平差计算。在GPS/BDS-2/GLONASS/Galileo 联合平差的情况下,其平差精度最高,用于高精度的数据处理时可优先考虑选择;在单星系统平差的情况下,GPS 在N、E、U 方向上的平差精度最高,因此GPS 是最优的选择;在双星系统联合平差的情况下,GPS/BDS-2在N、E 方向上平差精度最高,GPS/Galileo 在U 方向上平差精度最高,但由于GPS/BDS-2 平差坐标值与GPS/BDS-2/GLONASS/Galileo 的更吻合,在双星系统平差计算时可优先选择GPS/ BDS-2。

