基于简便运算的错题分析及对策初探

朱文娟

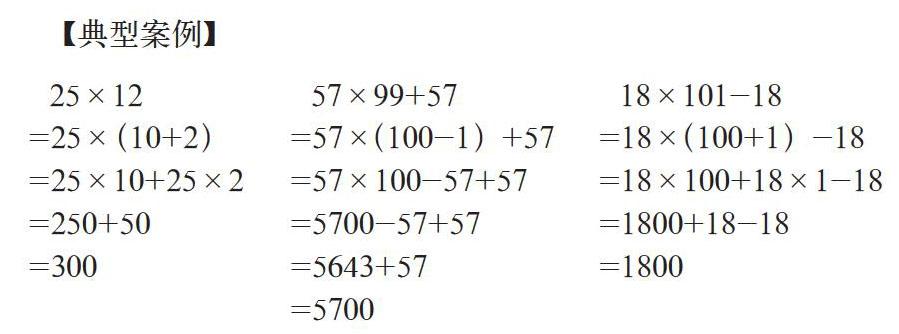
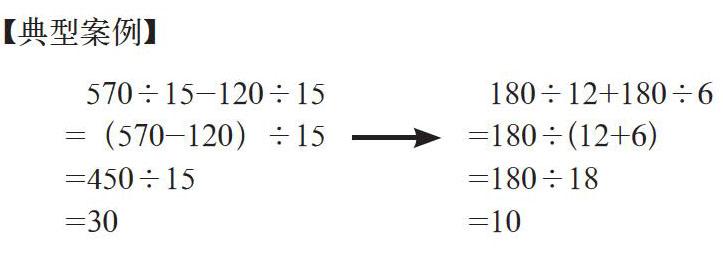
摘 要：简便运算是根据数的特征和运算的特征，依据运算律和运算性质简化复杂计算的技能，对培养学生的计算能力、应用能力起着重要的作用。可在教学中发现，很多学生把不能简算的简算了，能简算的不简算，针对此现象，笔者对自己班级中出现的简算错题进行了整理与分析，发现了四大主要致错原因，分别是乱凑整，思维定势下的按部就班，负迁移，不理解运算律的算理等，并试着提出了一些应对策略。

关键词：简便运算;分析;对策

简便运算是小学数学教学中“数与代数”的必学内容之一，要求学生能结合相关算式的特点，根据四则运算律或运算性质，在不改变运算结果的前提下灵活处理运算顺序，使算式简便易算。它能使学生思维的灵活性得到充分锻炼，对提高学生的计算能力、应用能力起到重要的作用。

例如：一年级上册学习9加几时，引导学生想到“几”哪里去借一个1，和9凑成10，这样加会比较简便;而加法、乘法竖式计算方法，问题解决中的某些不同算法等，不同程度上也运用了运算律。有了前期的铺垫，在四年级上册第四单元，教材安排了《运算律》这一课，学生开始系统学习这五大定律，并用之于简便运算。于是我将这些典型的错误整理起来，结合自身的教学经历以及对学生的研究，而后发现这些错误的背后有深层次的心理因素，主要可归纳为以下四个方面，并试着提出一些应对策略。

1 “条件反射”——乱凑整，忽视运算顺序

【典型案例】

【现象分析】不管哪个年级的学生都会出现这样的例子，当我们批改给他一个叉叉时，学生自己又能马上觉悟并予以订正，可下次遇到类似的题型还是会有不少人再次掉入出题者的“陷井”。如果第二题的题目是86×35+59，大多数学生就不会出现错误了。显然，题目中的+=1，35+65=100，25×4=100给了学生很大的“刺激”，他们忽视了运算顺序，把注意力集中在了数字凑整上。

【对策】学生对数敏感是件好事，但一看见“特殊的数字”，不管三七二十一就计算，却是聪明反被聪明误了，这在一定程度上也归咎于老师在平时的上课中过分强调可以“凑整”的数，而忽视了算式运算顺序的教学，从而在教学中要更加注重强化算式整体意识，在学生观察时，要加强引导他们将整体印象与细节观察相互补充。例如+×2和（+）×2，86×35+65和86×（35+65），25×4÷25×4和（25×4）÷（25×4）等不同算式，把学生的注意力引向算式的运算顺序，要向学生强调：算式整体，再进一步对算式中数的特征进行简便运算。使学生明确无论算式怎么变，算式的背后的运算顺序是不变的，切不可背离了运算的顺序。

2 思维定势，缺乏对数拆分的敏感度

【典型案例】

【现象分析】以上几题都不能算错，但却未真正达到简便之最。第一题，对于较“隐蔽”的用乘法结合律计算的题目，一些学生却常常习惯用乘法分配律计算，第二题和第三题，本来可以直接应用乘法分配律进行简算的算式，不少学生出现烦琐或者错误计算的现象。究其原因，有以下几个方面：首先，在学生眼里，两位数乘两位数，只要把其中一个乘数拆成几十和几就是简便运算了。25×12，可以将12拆成10+2，这恰好符合学生们的思维能力和感知规律，学生看到了整数10就觉得是簡便算法了。而把12分成3×4，25×4刚好能计算出整百，像这种更深入的简便方法的思维能力大多同学就没有意识到。经过老师多次点拨，学生或许下次看见25×12会把12拆成3×4，并牢记看见25就尽量去找4，可是当数字变大后，比如25×112时，学生很难会想到拆成25×4×28，因为112的分解已经不属于表内乘法，学生会避开112÷4的过程，只会将112拆成100+10+2。后面两题，由于是乘法分配律通常形式的反向运用，又与原乘法分配率基本形式的结构相比发生了一些变化，“乘加乘”的模式始终定格在学生们的思维中，当形式发生了变化，学生就“不识庐山真面目”了。

【对策】有些简便计算题本来就存在一题多解的情况，但对数合理拆分会使简便更简便，对于第一题的问题，教师应注重学生对数合理拆分的成功体验，提高学生对数的敏感度。例如25×48，先让学生讨论拆分哪个数，怎么拆分，然后将学生的不同拆分方法进行罗列，出现25×（40+8），25×4×12，5×5×4×12，48×（20+5）等不同形式。此时教师不必急于否定学生的拆分方法，也不必急于运用定律计算，而是先让学生进行对比筛选，把真正能运用运算律帮助我们简算的方法留下后再让学生动手计算，让学生体验不同的策略的优势，从而优化解题策略。

3 知识负迁移致错误猜想

【典型案例】

【现象分析】在学习了分配律之后，不少教师就会出一些125×34-25×34，84÷7-14÷7这样类似的姊妹题，结合乘法分配律，学生猜想84÷7-14÷7=（84-14）÷7=10，验证发现猜想是正确的，学生们犹如哥伦布发现新大陆一样欣喜，认为自己发现了除法分配律，即a÷b±c÷b=（a±c）÷b，于是当出现第二个题时，他们想当然认为类似的180÷12+180÷6=180÷（12+6）也是成立的。因之前有了乘法分配律和类似570÷15-120÷15=（570-120）÷15的知识体验，知识的负迁移造成了学生对位置排列上类似于分配律特点的除法运算，错误运用“除法分配律”去解决。

【对策】解决因负迁移导致的计算出错问题，教师既要在备课时预见这一常见的错误，引导学生辨析a×b±c×b与a÷b±a÷c，a÷b±a÷c与a÷b±c÷b的形式结构，用纠错练习方法来帮助学生找出它们之间的联系和区别，同时要充分利用因负迁移引起的错误资源，通过比较、辨析，分析出错的原因，寻找避免出错的方法，更要不轻易否定出错学生的计算方法，保护出错学生的自信心和创造力。

4 对运算定律的不理解

简便运算是拓展学生运算思路，提高运算速度，发展对数的意义和运算意义理解的有效途径，教师原以为教给了孩子简便的计算方法，却不料成了一些孩子的负担，简便运算对他们而言并不简单，在运算律之间徘徊，我想教师在教给孩子方法的同时应当将算理也和孩子讲清楚，平时注重简算能力的培养，并把生活和简算紧密结合，针对学生常出的简算错误进行原因分析想出对策，适当做一些变式练习，让孩子真正掌握简算的窍门，也让简算真正成为孩子们计算的好助手！

参考文献：

[1] 苏霍姆林斯基.给教师的建议.教育科学出版社，1984-06.

[2] 杨慧娟.小学生计算错误原因分析及对策[J].中小学数学.2009.9.

[3] 曹培英.关于小学数学学习心理的研究[J].小学数学教育，2002.5.

[4] 周超.数学学习的心理基础与过程[M].上海;上海教育出版社，2009.10.