例谈提升数学思维小专题复习课的设计原则

余雪娇

【摘要】郑毓信教授在《数学思维之深思》提出：数学教育应当致力于促进学生更加积极地进行思考。学生的主体作用和教师的主导作用应表现出能动性，这一能动性应统一在形式多样（动脑、动口、动手）的数学活动中。

【关键字】数学思维   小专题复习课   设计原则

【中图分类号】G633.6【文献标识码】A【文章编号】1992-7711（2020）08-064-02

现在流行的复习课形式基本上是知识清单加题海战术。学生不停地动手写，复习课就是习题课。重复机械的劳动，从应试的角度来看可以提高常规题的命中率，有其积极的一面。但学生缺乏时间动脑、动口;缺乏思维碰撞。一者，学生觉得数学乏味，另者不利于学生数学思维的培养。没有深层次的理解，不会变通，不灵活。小专题复习正是突破常规复习的形式，走出单纯的知识记忆模式，提升学生数学思维为主要目的一种复习形式。

小专题指的是以一道中等题目为主基调，抽出要学习的主题;通过“以退为进”，让学生“退”到题目的最基本概念和原理。再在“以小见大”部分解决新的问题，突出核心知识和数学思想的思维的训练。小专题着力点在于思维，其学案设计尤为重要。结合具体的例子谈谈设计要遵循的3个原则。

《直角三角形中求线段长度》学案

（A版）

一、以退为进

1. 在Rt△ABC中，∠A=90°，

AB=5，AC=12;

（1）求BC的长度.

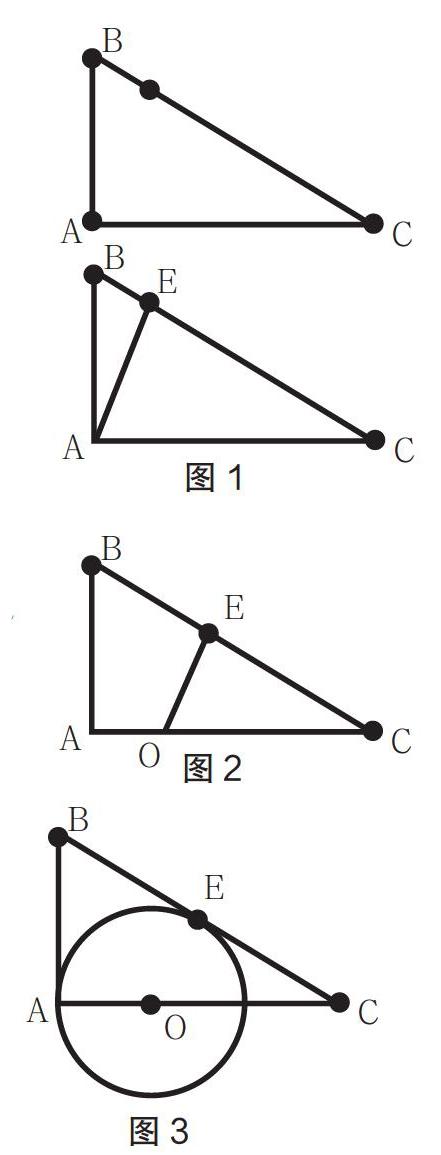
（2）如图1，若AE⊥CB于E，

则AE=          ;

（B版）

一、以退为进

1. 在Rt△ABC中，∠A=90°，

AB=5，AC=12;

（1）如图1，若AE⊥CB于E，

则AE=           ;

（2）如图2，若点O在AC上，

过点O做OE⊥CB，且

OC=8，求OE长。

二、以小见大

2.如图3，在Rt△ABC中，

∠A=90°， AB=5，AC=12，

点O在AC上，

⊙O切BC于点E，点A在

⊙O上，求⊙O的半径。

（你能想到几种方法？）

三、变式迁移

3.抛物线y=-x2-2x+3与x 轴交于A，B两点（点A 在点B的左侧），与y轴交于点C，顶点为D，连接AD，抛物线的对称轴与x轴的交点为E.抛物线的对称轴上是否存在点P使得点P到AD的距离等于点P到X轴的距离？若存在，请求出点P的坐标;若不存在，请说明理由。

一、以题点知，学习中心原则，提升学生思维的慎密性。（以退为进）

用简单的题目激活学生的已有知识。不是干巴巴的概念或定理的填空。学生通过完成题组形式，去唤醒知识点。设计时要考虑学生已有的经验，心理发展水平;要了解学情，尊重学生，因人制宜。针对不同的班级，设计的起点、幅度要相应的变化。让不同程度学生都能参与其中的数学活动中。A版设计适合于学生层次较低的，B版是层次较高的。以学生的学习为中心，针对不同层次学生适当的退。保证每位学生都有可完成的数学活动，都有可思考的问题。回归到原理或者基本概念的学，追根寻源。教师在学生学的过程中启发诱导，把几个零散的知识点用一条主线（主线可以是一个基本图形，例如图2）串联起来，形成知识链（相似、三角函数、等面积法、勾股定理）。形成学生良好的认知结构，提升学生思维的缜密性。

二、简化经典，凸显知识主干，提升思维的深刻性，广阔性。（以小见大）

中考的压轴题是命题者精心设置的，思维含量极高。但对大部分学生来说：偏难。教师可以选取某个点，略去其他无关的部分。化繁为简，适当的搭脚手架，降低难度，改编为中档题。不失为锻炼学生思维的上好素材。

例如：2016年广州中考24题：

已知二次函数y=mx2+（1-2m）x+1-3m与x轴相交于不同的两点A、B.

（1）求m的取值范围。

（2）证明抛物线一定经过非坐标轴上的一点P，并求点P坐标。

（3）当0.25≤m≤8时，由（2）求出的P点和A、B点构成的△ABP的面积是否有最值，若有，求出最值及相对应的m值，若没有，请说明理由。

我们可以把中考真题从不同角度进行改编。若选取面积作为小专题，则可以抛弃恒过定点问题;如果恒过定点问题，则可抛开面积最值。改编后放在以小见大的位置，着重在于解题背后的思想方法提炼。通过师生、生生交流，分享而引发思维碰撞。

第2题是把原题中的直角坐标系去掉，保留核心主干改编题。本题的方法较多，至少有五种方法。学生先是独立的思考完成，进而交流。不同的解法，收获不同的思维。教师可以适时提出问题：

1.“以小见大”与“以退为进”的题有什么异同点 ？

2.你是怎样想到这种解法？不同解法之间的有什么共同点？那些解法是可以推广的？

3.你可以提出什么样的问题，或者说这题可以有怎么样的变式（从动态的观点看o点运动，例：o点在线段CA的延长线上）。

学生围绕着这些问题，又进入新的学习、交流。抓住生成会使课堂大放光彩，让复习课有新意。不是炒冷饭，从而焕发生机。这样精心改编设置的题不仅融合了核心主干知识，还在简单的题目中培养学生审同辨异同，同中观异的好思维。学生经过思考，交流，再现核心知识，最后通过新问题的讨论学习，使理解进入更高层次，是深度的理解。当知识发生过程成为一个有内在需求的，非被动接受的过程时，才能更好的主动建构知识体系。教师及时的归纳，渗透数学思想方法，比如转化与化，归特殊到一般，分类等。学生感悟数学理性的精神，提升思维的深刻性，广阔性。这种解题背后的思考，才能把相應的解题行为看作是真正的数学活动，即由单纯的“问题解决”过渡到“数学思维”。学生才会更深刻的理解知识本质，题型特征，提升思维，能得心应手的解决一大类问题。就像由一颗树看到几颗树甚至是一片森林，起到以小见大的作用。

三、聚焦基本点，题与题之间连贯性原则，提升思维的灵活性敏捷性

现代认知心理学认为：理解，无非就是指新学习的知识与主体已有的知识与经验之间建立了直接的联系（包括同化与顺应），其程度也完全取决于联系的数目和强度。如果潜在的相关的各个概念中，心理表征只有一部分建立联系或者说联系脆弱，这时的理解是有限的。小专题学案在设计上必须围绕一个主题，以退为进，以小见大，变式迁移的三个环节中，题与题之间必须是相关联的（题量不宜多，4题左右）。体现的均是同一块核心知识的本质属性。只是呈现形式不一样罢了。例如第1题仅仅是直角三角形斜边上的高，第2题添加圆背景，第3题就在直角坐标系下抛物线的背景，并把静态问题变为动态问题。这3个题目是一脉相承的，本质特征都是直角三角形中求线段长度，但又有其不同的地方。在特定的背景下，又会有特定的方法。例如直角坐标系可以从函数角度求线段，思路会更宽更广。这种注重题与题之间的联系，可以使学生对已学的知识有更深刻的认识，可以较为系统的把握知识间的逻辑。便于比较、鉴别、取舍、融合。能在新背景下较快地找到解题的突破口，提高了思维的灵活性与敏捷性。

数学新课标指出：思维能力主要指会观察、实验、比较、猜想、分析、综合、抽象和概括;会归纳、演绎、类比进行推理;合乎逻辑的准确的阐述自己的思想和观点。小专题在题量少，相互联系中，给时间和空间，让学生观察，思考，抽象，概括表达，对提升数学思维有积极的意义。

[参 考 文 献]

[1] 刘永东.例谈数学小专题复习的策略和应用[J].教育导刊（上半月）2013（1）.