基于拓扑优化技术的某轿车拖钩强度分析设计

周德生 胡冬青

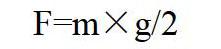
摘 要：为了提升汽车拖钩结构强度，根据国标GB32087-2015《轻型汽车牵引装置》的要求，在HyperMesh软件中建立某车型后拖钩强度的有限元模型。首先，利用ABAQUS/Standard求解器进行拖钩强度分析，预测结构的风险区域，同时，应用CAE拓扑优化技术对其进行优化分析和改进设计，改进后的结构满足强度分析要求。最后，对改进方案的结构进行拖钩强度试验验证，结果表明改进方案满足设计要求，从而验证了拖钩强度有限元模型的准确性，为拖钩强度分析和优化设计提供依据。

关键词：拖钩;强度;拓扑优化;改進方案

Abstract： In order to improve the strength of car towing hook， according to national standard GB32087-2015《towing devices for light-duty vehicle》， The finite element mode was built by HyperMesh software. Firstly， the strength analysis of towing hook was carried out by the ABAQUS/Standard solver module， which can be used to predict the hazard area of structure. Meanwhile， the optimization analysis and improvement designing of towing hook structure strength were used by CAE topology optimization， the improvement program shows that the result meet the strength requirement. Finally， the strength test verification of the improvement program structure was carried out， the results showed that the improvement program meet the design requirement. Thus， the accuracy of the finite element model of the towing hook strength was verified， which provided towing hook strength analysis and optimization design.

Keywords： Towing hook; Strength; Topology optimization; Improvements program

前言

拖钩是汽车上一种安全装置之一，当汽车损坏失去动力时，可以借助外力使其走出困境，因此拖钩及其安装板都应具备足够的强度[1-2]。因为拖钩使用过程中会遇到如转弯、加速、制动、过减速带等极限工况，主要受力零部件包括牵引钩、防撞梁、纵梁及牵引钩套管及加强板等。当装置中任一受力部件强度不足或结构损坏时，牵引装置将失效[2-5]。因此，为了节省开发成本、时间等资源，在概念设计阶段时须通过强度分析，并结合CAE优化技术进行优化分析改进设计，为拖钩的前期设计提供参考和指导。

本文根据国标GB32087-2015《轻型汽车牵引装置》的要求[6]，在Hypermesh软件中建立某轿车后拖钩的有限元模型[7]。对轿车拖钩结构进行变形、塑性应变分析，确定拖钩结构的风险部件，并应用CAE拓扑优化技术进行分析，结合三维建模软件进行改进设计，通过多轮的优化分析和改进设计，得出螺管安装板的最佳改进结构。根据改进方案的结构进行了拖钩强度试验验证，最终通过了拖钩强度试验要求，也充分验证改进方案的有效性和可行性。

1 拓扑优化方法

1.1 拓扑优化方法

结构的拓扑优化过程实际是在给定的设计区域内寻求最优材料分布的问题。通过不断的优化迭代计算，保留对结构传力路径有利的结构单元，而删除对结构传力路径作用不大的单元，能够高效地实现最佳结构。其本质是一个对单元集合中的单元进行增删的离散型优化问题[8-9]。

拓扑优化常采用连续变密度方法[10-11]，即SIMP方法（Solid Isotropic Material with Penalization）。从根本上说是离散变量0，1的组合优化问题，即通过确定变量为0或者1来决定结构单元是否被删除。基于SIMP 方法的拓扑优化模型可广泛应用于各种性质的目标函数和约束条件的场合，如最小柔度问题，最小特征值问题，最小重量问题等。

基于变密度理论SIMP法的连续型拓扑优化问题的数学模型可表达为：

式中：目标函数C定义为结构的总体柔度，F为力向量，U为位移列阵，K为优化前的结构总刚度矩阵，V0为整个设计域的初始体积，V是优化后的结构体积，f为优化体积比。

连续体结构拓扑优化问题有设计变量、目标函数、约束条件三要素，其定义如下：

设计变量：拓扑优化中一般采用结构单元的相对拓扑密度作为优化设计变量，式（1）中的优化设计变量定义为单元相对密度x={x1 ，x2 …，xi}T。

目标函数：常采用结构的体积和质量，或者结构柔度、位移、频率等作为设计目标。另外，在多目标优化设计中也可以采用结构响应的组合函数作为优化目标。式（1）中采用结构的整体柔度作为目标函数。

约束函数：可以采用结构优化的体积比，或者结构的整体响应，如结构柔度、位移、频率等作为约束。式（1）中采用结构体积的百分比作为优化约束函数。

2 加载边界条件和工况要求

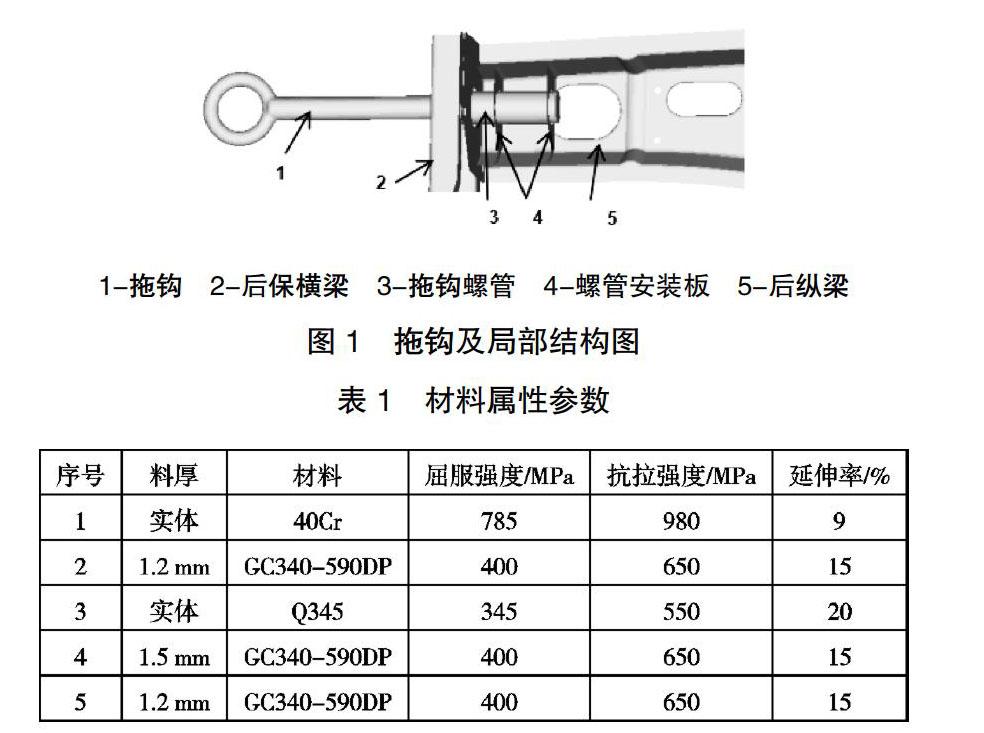
本文以某轿车后拖钩为例，为提高计算效率，截取白车身后半部分，拖钩及局部结构如图1所示，材料属性参数如表1所示。

依据GB32087-2015《轻型汽车牵引装置》的要求，牵引装置应能承受的最小静载荷F 为：

式中：F牵引装置承受的最小静载荷，单位为牛（N）;m最大允许总质量，单位为千克（kg）;g为重力加速度，9.8 m/s2。

依据GB32087-2015《轻型汽车牵引装置》的要求，拖钩强度试验可分解为四个加载工况。

工况一：垂直方向向上5°拉壓：在拖钩上沿x向向上偏斜5°施加F载荷，并按照拉伸、卸载、压缩、卸载的加载顺序进行，如图2所示。

工况二：垂直方向向下5°拉压：在拖钩上沿x向向下偏斜5°施加F载荷，并按照拉伸、卸载、压缩、卸载的加载顺序进行，如图2所示。

工况三：水平方向向内25°拉压：在拖钩上沿x向向内偏斜25°施加F载荷，并按照拉伸、卸载、压缩、卸载的加载顺序进行，如图3所示。

工况四：水平方向向外25°拉压：在拖钩上沿x向向外偏斜25°施加F载荷，并按照拉伸、卸载、压缩、卸载的加载顺序进行，如图3所示。

根据GB32087-2015 《轻型汽车牵引装置》的要求，在完成拖钩强度试验后，牵引装置及其固定件不应出现失效、断裂或产生影响正常使用的变形，以及损坏牵引装置附件的其他部件。结合CAE分析方法和实践经验，将仿真分析结果转化为设计指标，即仿真分析时加载点最大位移小于10mm，残余位移小于1mm;结构件的最大塑性应该小于2%。

3 拖钩强度分析及拓扑优化

3.1 拖钩强度分析

根据国标的要求和上述分解的四个工况，对拖钩强度模型进行仿真分析，分析结果如表1所示，从表中可知，工况一和工况二的分析结果比较接近，查看两个工况的结构的塑性应变云图，其风险区域也相似;工况三、工况四的分析指标值也比较接近。工况三的分析结果是四个中最恶劣的，以工况三作为案例进行分析，其加载点最大位移为14.0mm，超过目标值10mm，如图4所示;而残余位移为5.8mm，也超过目标值;特别是塑性应变，最大值为16.9%，超目标值和材料的延伸率，有断裂的风险，存在安全隐患。四个工况中除了后纵梁和螺管安装板的塑性应变超目标值，其它结构件塑性变形都小于目标值，失效风险小。后纵梁的最大塑性应变位置发生在跟螺管安装板的焊点处，不属于危险区域，如图5（a）所示;而螺纹安装板的最大塑性应变为16.9%，发生跟螺管连接处，在安装板的折弯处也出现较大的塑性应变，其值为16%，属于失效的风险点。由此可知，拖钩结构不满足强度要求，以此结构进行拖钩强度试验时，断裂失效的风险非常大，有必要借助CAE优化技术，提高其结构强度，以达到目标要求。

3.2 拓扑优化分析

根据以上强度和变形分析结果，拖钩强度分析结果不能满足要求，需要对拖钩结构进行优化分析和改进设计，从而提高其强度和抗变形能力。改进方案可以从两方面进行，第一针对位移过大问题可以加强拖钩本身的刚度，即通过缩短拖钩的长度或者增大拖钩的外径，受到造型的影响，可能性非常小;第二针对拖钩螺管安装板强度不够问题，可直接增加安装板和纵梁的材料厚度，但会增加重量和成本，或应用CAE拓扑优化技术进行重新设计，而本项目还处于项目的概念开发阶段，因而可保证在不改变其他结构的情况下，应用拓扑优化技术，对螺管安装板进行拓扑优化和改进设计。

把原螺管安装板的区域作为拓扑优化设计空间，在HyperMesh软件中处理后的设计空间材料分布如图6所示。为使安装板结构满足强度性能要求下的质量最小的目的，本次优化目标为材料体积最小，同时设置加载点的位移为最小，拓扑优化材料按照整车坐标系X、Z 轴对称分布，另外为了能使拓扑优化结果有很好的加工性，设定优化区域的材料沿整车坐标系X方向进行拓扑优化。

经过15次迭代计算后，拓扑优化后的材料分布如图7所示。由于结构的拓扑优化仅仅考虑了结构本身材料的一种最优分布形式，没有考虑加工制造、生产工艺和成本等因素，优化后结果是一种不规则的空间形状，一般是无法获得精准的材料分布或零件尺寸，可能导致制造难度与提高生产成本，所以在详细设计中须对拓扑优化结果进行改进设计[8-10]。

3.3 改进方案强度分析

拓扑优化结果的材料分布图形并不是真实的结构，其结果也无法直接应用到实际设计中，但可以为结构的设计提供参考，只有转化为具体的结构方案后才有意义。因此需要将拓扑优化后的结果在CAD软件中进行重新建模，同时结合形貌、尺寸等优化手段，进行反复的优化分析，最终得到最优的方案。根据拓扑优化的结果对螺管安装板进行重新建模设计，进过多轮优化分析和强度校核后，最终优化改进后的拖钩结构如图8所示。上下层安装板通过点焊跟后纵梁连接，而拖钩螺管跟安装板支架通过二氧化碳保护焊进行连接，改进方案拖钩装配局部结构如图8所示。

根据最终的改进方案结构进行了拖钩强度分析，四个工况分析结果如表3所示。各工况的最大位移为4.6mm，如图9所示，小于目标值10mm的要求，最大残余位移为0.5mm，也小于目标值1mm，而最大塑性应变为1.6%，小于2%的目标值。虽然各项指标的极值都发生工况三的分析结果中，但都是满足仿真分析要求的。如图10为工况三的塑性应变云图，从图中可以看出拖钩最大塑性应变发生在拖钩螺纹管安装板处，其塑性应变值低于目标值2%的要求，也远低于各自材料的最大延伸率值，断裂失效的风险很小。从四个工况分析结果可知，改进方案的分析结果能满足各项指标值，满足强度分析和设计要求。

4 拖钩强度试验

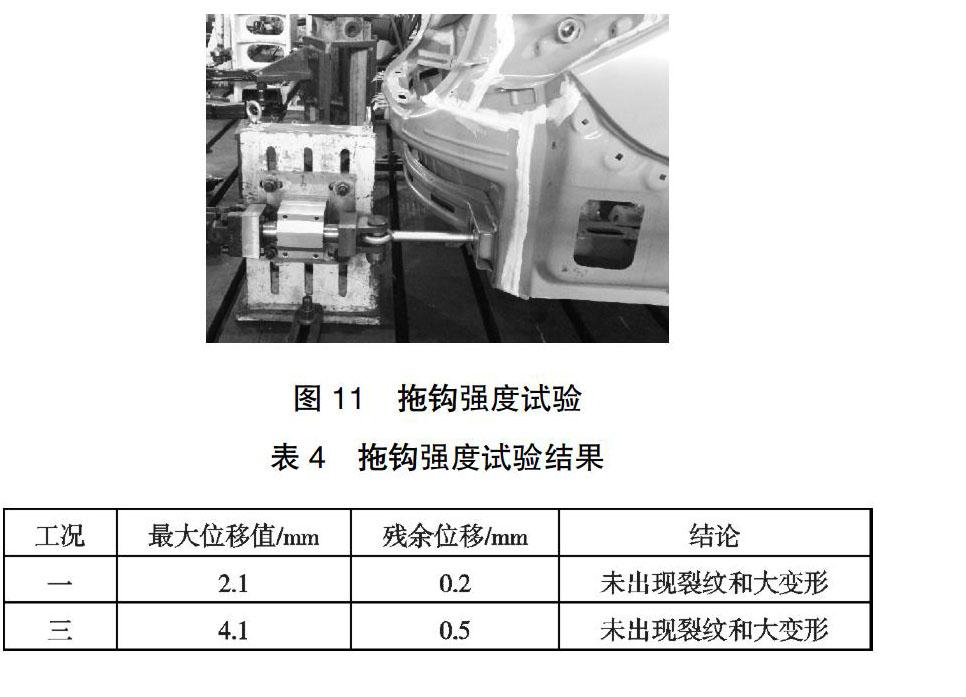
为了验证改进方案的拖钩结构强度的可靠性，根据最终的优化改进结构完成了该项目ET阶段的样车设计和制造，并按照GB32087-2015《轻型汽车牵引装置》的要求，在如图11所示的台架上进行拖钩强度试验。为了节约开发成本和提高效率，根据强度仿真分析结果，只进行了工况一和工况三的强度试验，试验结果如表4所示。从表中可知，工况一的最大位移为2.5mm，残余位移为0.4mm，而工况三的最大位移为3.8mm，残余位移为0.8mm，两工况试验后都未出现裂纹或者大变形等，满足拖钩强度试验的国标要求，试验结果验证了改进方案的可靠性。

对比表3的仿真分析结果和表4的试验结果，仿真分析结果的最大位移比试验结果略大，其误差在工程可接受的范围内，也说明了有限元分析结果是可信的，为后续研发项目提供优化思路和设计方案。

5 结语

本文通過对某轿车后拖钩进行强度分析，得到拖钩结构的危险部件，然后应用CAE拓扑优化技术，通过多轮优化和改进设计，并得到最终的改进方案。

通过对改进方案的结构进行拖钩强度试验，试验结果满足国标要求。试验结果表明改进方案可实施性、可靠性，也说明CAE技术对于提高拖钩结构分析和改进设计具有一定的指导意义。

参考文献

[1] 漆杰，童杰.基于CAE分析的汽车牵引装置优化设计[J].农业装备与车辆工程，2016（9）：62-65.

[2] 王峻峰，乔鑫.某轻型汽车前端牵引装置强度有限元分析与优化. 2014年中国汽车工程学会年会论文集[C].北京：机械工业出版社， 2014：793-796.

[3] 明宇.基于CAE技术的轿车拖钩分析与结构改进[J].汽车实用技术，2016 （1）：151-154.

[4] 傅薇，张影.轿车拖钩强度分析[J].合肥工业大学学报（自然科学出   版），Vol.32 No.Sup Nov.2009：101-103.

[5] 尚宝玲.关于房车拖钩强度分析以及优化[J].轻型汽车技术：2015 （1/2）：30-34.

[6] GB32087-2015《轻型汽车牵引装置》[S].中国标准出版社：2015.

[7] 王钰栋，金磊，洪清泉，等.HyperMesh&HyperView应用技巧与高级实例[M]：机械工业出版社，2012.

[8] 洪清泉，赵康，张攀，等.OptiStruct & HyperStudy理论基础与工程应用[M]：机械工业出版社，2012.

[9] 张伟，侯文彬，胡平.基于拓扑优化的电动汽车白车身优化设计[J]. 湖南大学学报（自然科学版），2014（10）42-48.

[10] 尹艳山.基于变密度法的连续体结构拓扑优化[D].沈阳：东北大学，2014.

[11] 朱剑峰.结构拓扑优化理论及在轿车副车架开发中应用研究[D]. 北京：北京理工大学，2015.