地铁车辆连续测力轮对仿真与试验研究

钟旭婕，寇 杰，张济民，王承萍

（同济大学铁道与城市轨道交通研究院，上海201804）

1 引言

轮轨作用力作为轨道车辆运行安全性的重要评价指标一直作为车辆线路安全性测试的重要选项，现有轨道车辆线路测试中有多种轮轨力测量方法。TB/T 2360-93 中列出了辐条式测力轮对、辐板开孔式测力轮对的间断测力轮对原理，辐条式测力轮对、辐板测力轮对的连续测力轮对原理[1]。通过在车轮几个半径上的合理组桥来尽量消除车轮转动的影响，然后求解多个非线性方程组而得到横向力、垂向力以及轮轨作用点位置[2-5]。文献[6]研究了根据车轮横向变形测量轮轨横向力的方法。文献[7]对比分析了1：5车轮上分别采用简易余弦桥和直流桥法的测试精度，分析结果表明简易余璇桥有更高的测试精度，测量结果更接近实际轮轨作用力。文献[8]通过元仿真的手段对400km/h 速动车组的车轮进行了静态载荷模拟计算。文献[9]利用仿真技术对连续连续测力轮对的最佳贴片位置选择进行研究。文献[10]利用有限元分析方法和数字试验方法寻找测力轮对最佳贴片位置。文献[11]将轮对标定试验台加载分为位置同步和力同步两个环节，分别应用主从式和交叉耦合式同步控制，很好的提高了系统的同步性能。以上文献基本均采用有限元仿真与数字分析相结合的模拟分析技术，未进行实际测力轮对贴片标定实验。利用某地铁车辆测力轮对，在有限元仿真和数字分析的基础上，进行了连续测力轮对的贴片、组桥和标定工作，可以为轨道车辆的连续测力轮对开发提供仿真及试验经验。

2 连续测力轮对原理

想要实现连续测力，测力轮对上贴片位置以及组桥方式是关键。采用余弦桥法，进行测力轮对的测试。当车轮旋转时，垂向力P 和横向力Q 均为时间函数，在相对于起始位置，车轮向前滚动任意角度θ，任意时刻t，车轮辐板某处的径向应变为时间和角度的函数：

相同半径的系数kpi和kqi相等，不同半径不等。

通过组桥构造的方法可以使角度函数为余弦函数即：

通过式（3）和式（4）反向计算可以得出轮轨垂向力和横向力的计算公式如下：

式中：垂向力p 恒为正，因而可以通过平方和在开根运算求得。而横向力在会出现正负值差别。

根据理论公式分析可以得出，获得连续测力的前提是找到合适半径的径向应变，通过合理的组桥方法，使应变数据和垂向载荷以及横向载荷间的比值系数呈余弦函数规律变化。

3 虚拟组桥分析

为分析轮对辐板上合适的应变片粘贴位置，先利用有限元计算得出轮对在垂向力和横向力的作用下的轮对辐板应力分布。根据地铁企业给定的轮对参数，在Ansys 建立LMA 型踏面轮对，模型共513600 个单元，杨氏模量和泊松比分别为2.1e11Pa 和0.3，材料密度为7800kg/mm3。利用Ansys 对曲辐板式轮对进行横向和垂向载荷计算，计算在不同载荷作用下轮对辐板表面径向应变大小，选取合适的测力轮对径向应变片粘贴半径。

3.1 有限元加载计算

在车轴左右轴承作用位置定义6 自由度的固定约束，在左右车轮轮轨接触位置的接触节点处分别加载垂向作用力10kN，如图2.1 所示。如图2.1 所示，在车轴中央位置定义纵向和横向的平动约束，在左右车轮轮轨接触位置的接触节点处分别加载方向均指向轮缘侧的横向作用力10kN。

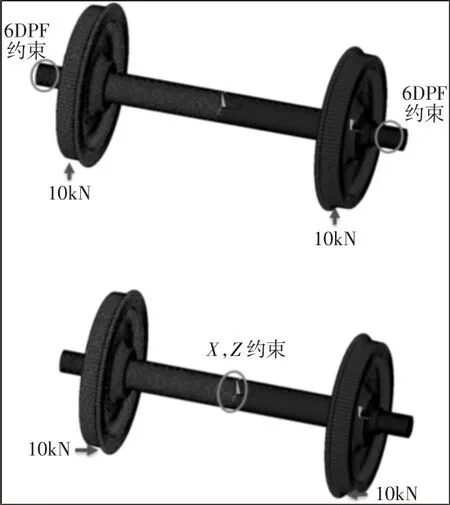
图2 .1 垂向和横向加载示意图Fig.2.1 Vertical and Lateral Loading Schematic

3.2 应变数据谐波分析

车轮辐板的径向应变是一个关于圆周角的函数，此函数具有谐波性，即车轮的径向应变可分解为多个简谐函数之和。

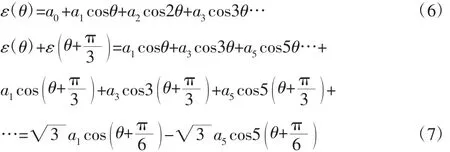
图2 .2 消除偶次和三次谐波贴片组桥方案图Fig.2.2 Eliminate the Even and Third Harmonic Patch Bridge Scheme

通过图2.2 的贴片和组桥方案可以消除偶次谐波和三次谐波，使桥路输出应变值接近余弦波。通过谐波分析求出组桥后的第一阶谐波的系数，在垂向和横向加载工况下，分别输出辐板外侧不同半径的一圈节点径向应变数据，利用谐波分析法，分析应变数据随角度变化的函数的一阶谐波分量。观测半径为（170～230）mm，每间隔4mm 取一个半径观测，共15 个应变观测半径。从图2.3 可以看出，垂向加载和横向加载下，应变余弦桥输出数值经过谐波分析后，从观测半径1 到观测半径15，第一阶系数a1的值均先增大后减小，并且在观测半径7 和观测半径8 附近达到最大，此时半径为200mm。为了使组桥后输出值足够大，保证测试的灵敏度且两个半径下的应变片可以方便布置，最终选定应变片在车轮辐板外侧的布置半径为195mm 和210mm。

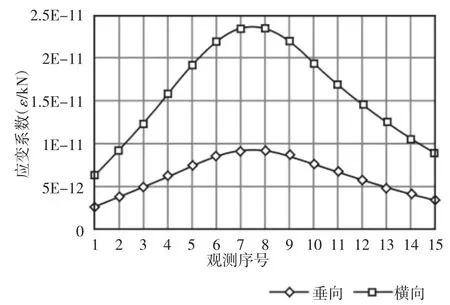
图2 .3 各观测点第一阶系数Fig.2.3 First Order Coefficient of Each Observation Point

4 试验台标定试验

根据有限元分析和数值虚拟组桥，选定应变片布置半径后，设计出的应变片布置方案，如图3.1 所示。分别在车轮辐板外侧195mm 和210mm 两个半径的圆上布置两个全桥，全桥的应变片圆周位置根据消除偶次和三次谐波贴片组桥方案选定，如图2.3所示。

图3 .1 应变片布置图Fig.3.1 Strain Gauge Layout

将应变片分别径向布置于图3.1 所示指定位置，完成全桥组桥和封装工作，将测力轮对放置于测力轮对标定试验台，如图3.2所示。测力轮对安置到位后，将全桥引出线经过集流环后连接至全桥应变数据采集设备。

图3 .2 测力轮对放置于试验台Fig.3.2 Force-Measuring Wheelset Placed on Test Bench

将测力轮对圆周360°等分为12 份，每30°为一个测试角度点。在12 个测试角度点分别进行横向和垂向加载测试。垂向加载方案为：左右两侧轴箱上方分别设置一台液压千斤顶，利用液压千斤顶同步对测力轮对左右车轮施加垂向载荷，施加载荷为（0～70）kN，按10kN 的载荷梯度分7 次施加；横向加载方案：通过左右两根顶杆，将横向布置的液压千斤顶的作用力施加于轮对内侧，施加载荷为（0～40）kN，按10kN 的载荷梯度分4 次施加。左右车轮下方分别布置了一台三向测力传感器，传感器上方分别固定有一段与车轮踏面相接触的模拟钢轨，当在轴箱和车轮内侧施加载荷时，三向测力传感器可以测试轮轨接触位置车轮所受的作用力，采用模拟钢轨与三向测力传感器相结合的方案可以更加真实准确地模拟实际轮轨接触作用力。

图3 .3 加载方案示意图Fig.3.3 Loading Plan Diagram

5 标定结果分析

5.1 横向标定

计算各载荷等级下，应变片全桥数据与横向力数据，计算应变全桥电压输出值与垂向力数据斜率系数值。计算结果，如图4.1所示。

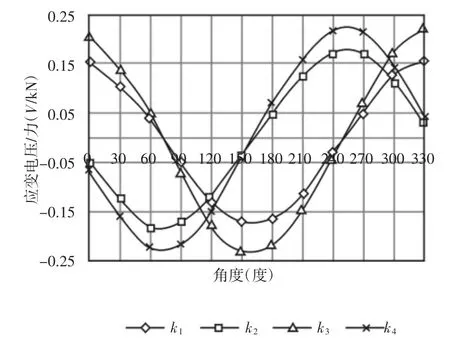
图4 .1 四个桥横向变系数Fig.4.1 Lateral Strain Coefficients of Four Bridges

从图4.1 可以看出，四个全桥的电压输出数据与作用力计算所得的横向应变系数基本均随加载作用角度成余弦函数变化，且相差90°布置的两个全桥间全桥1 和全桥2，全桥3 和全桥4 的横向应变系数余弦曲线相位基本相差90°。同时在相同角度不同半径布置的全桥1 和全桥3，全桥2 和全桥4 的横向应变系数曲线相位一致。在Matlab 中对离散数据点进行三角函数拟合，分别求出一阶三角函数的系数值，计算结果如下：

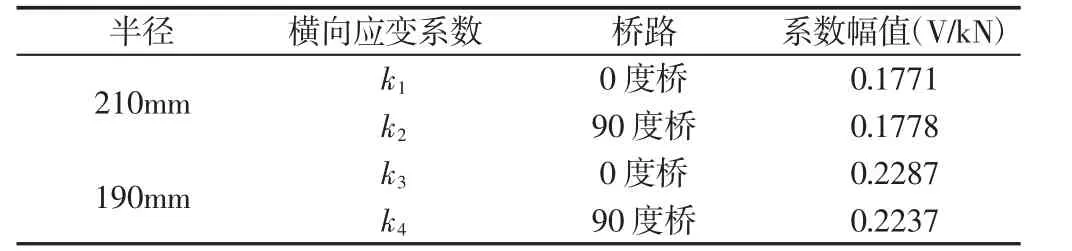
表1 横向应变系数拟合幅值Tab.1 Lateral Strain Coefficient Fitting Amplitudes

从表1 可以看出横向应变系数k1和k2，k3和k4相差均在5.0%以内，标定结果可信度较高。因此横向标定系数k1q和k2q可由相应半径的应变系数平均得出。

5.2 垂向标定

计算各载荷等级下，应变片全桥数据与垂向力数据，计算应变全桥电压输出值与垂向力数据斜率系数值。计算结果，如图4.2所示。

图4 .2 四个桥垂向应变系数Fig.4.2 Vertical Strain Coefficients of Four Bridges

从图4.2 可以看出，四个全桥的电压输出数据与作用力计算所得的垂向应变系数基本均随加载作用角度呈余弦函数变化，且相差90 度布置的两个全桥间全桥1 和全桥2，全桥3 和全桥4的应变系数余弦曲线相位差为90 度。同时在相同角度不同半径布置的全桥1 和全桥3，全桥2 和全桥4 的横向应变系数曲线相位一致。在Matlab 中对离散数据点进行三角函数拟合，分别求出一阶三角函数的系数值，计算结果如下：

表2 垂向应变系数拟合幅值Tab.2 Vertical Strain Coefficient Fitting Amplitudes

从表1 可以看出垂向应变系数k1和k2，k3和k4相差均在5.0%以内，标定结果可信度较高。因此垂向标定系数k1p和k2p可由相应半径的应变系数平均得出。

由标定试验可以得到垂向标定系数k1p和k2p及横向应变系数k1q和k2q。根据式（3）～式（5），只需要测试出全桥1～4 的输出电压即可计算出轮轨接触垂向力和横向力。

6 结论

利用某地铁车辆测力轮对，在有限元仿真和数字分析的基础上，进行了连续测力轮对的贴片、组桥和标定工作。并得出以下结论：（1）根据仿真计算和虚拟组桥结果得出需要在车轮辐板外侧半径为195mm 和210mm 两个半径的圆上布置两个全桥。全桥组桥可以消除应变随角度变化函数的偶次及三次谐波值，实现近似余弦变化特性，组成余弦桥。（2）标定试验中在左右车轮下方分别布置了一台三向测力传感器，传感器上方分别固定有一段与车轮踏面相接触的模拟钢轨，当在轴箱和车轮内侧施加载荷时，三向测力传感器可以测试轮轨接触位置车轮所受的作用力，采用此方案可以更加准确地模拟实际轮轨接触作用力，提高标定测试精度。（3）通过圆周一圈12 个角度测试点的横向及垂向标定试验，根据车轮辐板上布置的全桥1～4 的输出电压值随载荷线性变化，计算线性斜率系数。全桥输出电压随载荷变化系数均呈余弦特性，且90 度布置的两个全桥间的应变系数余弦曲线相位相差90 度。通过三角函数拟合后计算得出垂向标定系数k1p和k2p为0.0078145 和0.008088 及横向应变系数k1p和k2p为0.17745 和0.2262。根据余弦桥计算公式，线路试验时只需要测试出全桥1～4 的输出电压即可计算出轮轨接触垂向力和横向力，实现连续轮轨力测试。