基于灰色二次回归的轴温预测模型

王 超，邹益胜，邓佳林，罗怡澜

（西南交通大学机械工程学院先进设计与制造研究所，四川 成都 610031）

1 引言

随着机车车辆运行速度的提高，运行安全显得尤为重要，必须在提升速度的同时保障旅客的人身安全。轴箱轴承作为列车走行部的关键零部件，一旦发生故障，严重时可造成列车脱轨，产生运营事故[1]。由于正常轴承在运转过程中有一定的温度波动范围及热平衡线，而故障轴承则内部振动增大、摩擦增大使得轴承产生的热量增加，最终导致轴承温度高于正常轴承的温度波动范围，因此可以使用温度作为判定轴承是否正常工作的指标。

车载轴温监测报警系统被设计用来监测列车转向架上各轴承的温度，通常分为暖轴预警及热轴报警两个等级，均由一定设定的温度限及流程逻辑进行控制[2]。如果轴温报警系统发出报警信号，则必须进行停车处理，严重影响行车调度，同时也造成不良的社会影响和较大的经济损失。因此，如果能够预测轴温的发展趋势，便可争取更充足的处理时间，以便采用更多的处理手段来保障行车安全、同时降低社会影响和经济损失。

在基于时序的经典预测模型中，灰色模型由于建模样本量小、计算效率高和短期预测精度较高等特点，得到了众多研究者的青睐。其中GM（1，1）模型是在预测领域使用最为广泛的模型之一，通过一阶微分方程及一阶累加算子进行构造[3]。同时，对GM（1，1）模型的改进也在不断研究当中，模型的改进主要分为三个方面[4]：（1）原始序列数据变换方面，文献[5]提出一种“幂函数-指数函数”复合变换的数据变换形式；（2）模型背景值方面，文献[6]使用遗传算法优化背景值建立了ITGM（1，1）模型；（3）模型建模机制方面，文献[7]构建了差值GM（1，1）模型。

值得提出的是，已有学者使用灰色理论模型进行机车车辆的轴温预测研究：如文献[8]基于固定数值的新陈代谢GM（1，1）模型对相对温升进行单步预测，为研究提供了借鉴思路。

在采用GM（1，1） 模型对高速列车轴温进行多步预测研究中，发现存在以下问题：（1）所采集到的轴温数据为整数，数据平滑性不好，导致预测结果误差较大；（2）在轴温升降趋势变化的拐点处预测误差较大。针对上述问题，首先采用对轴温数据进行迭代三次的滑动平均处理，提高数据的平滑性，再通过引入二次多项式与GM（1，1）模型融合重构，形成灰色二次回归轴温预测模型，提高了拐点处的轴温预测精度，且在轴温的单调变化区间保持了GM（1，1）模型的精度。以某高速列车轴温数据为例，分别对轴温先升后降、先降后升和连续波动三种典型样本进行后序5min 多步预测，通过预测结果和实际数据的对比发现，这里重构模型的预测精度全面优于GM（1，1）模型，从而验证了这里方法的有效性。

2 基于GM（1，1）的轴温预测模型

设一组原始时间序列的轴温数据为：

使用GM（1，1）模型对轴温进行预测的步骤如下：

（1）确定一定的建模数m≥4 和预测点数s，即使用m 分钟的轴温数据预测未来s 分钟的轴温数据，当轴温数据积累到满足建模时即可开始预测。

（2）对建模数据进行预处理，再将处理过的数据作为GM（1，1）模型的原始序列带入GM（1，1）模型进行计算，得出m 个点的模拟值和s 个点的预测值。

（3）每当得到新的轴温数据点时，使建模窗口内的数据吐故纳新，将最新的数据纳入，最老的数据移除，再通过数据预处理后进入GM（1，1）模型，从而构成新陈代谢GM（1，1）模型。在保证建模数不变的情况下，纳入最新趋势数据，削弱老数据对现在趋势的影响，从而提高预测精度。

（4）将第一次求得的m 个模拟值及s 个预测值同之后每次求得的第s 个预测值拼接起来，即可得到完整的基于GM（1，1）的轴温预测结果。

3 建模数据的平滑处理方法

现实中，由于车载轴温数据存在每分钟采集一次且数据为整数等问题，因此必须对轴温数据进行平滑处理以提高其平滑度，进而提高预测模型的预测精度。

若使用曲线拟合方法对轴温数据进行平滑处理，则不同的核函数会导致平滑后的温升趋势趋近于所选择核函数特定的趋势，进而改变了原始轴温数据的温升趋势，而滑动平均处理则不会改变数据的固有趋势，因此选择使用滑动平均的数据预处理方式对轴温数据进行平滑处理。

滑动平均处理后的结果可再次滑动平均以进一步提高数据平滑度和预测结果精度，但平滑次数过多会使得数据过于平稳导致数据失真，使得预测模型无法获取温升趋势，最终导致预测精度不高。根据对比实验，选择进行迭代三次的滑动平均。经过迭代三次滑动平均的GM（1，1）预测结果在预测精度及平稳性方面均较好，如图1 所示。

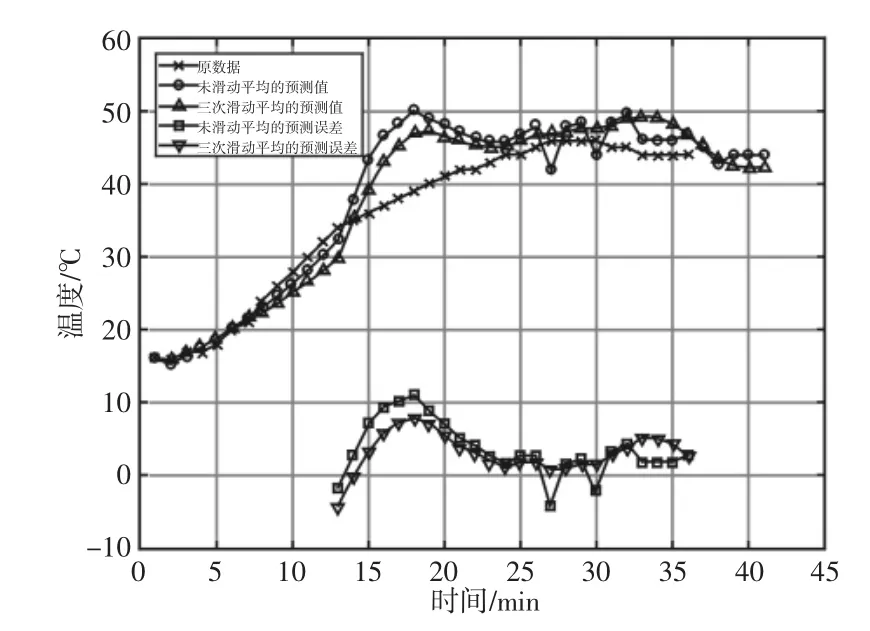
图1 有无滑动平均处理的5 分钟预测结果对比Fig.1 Comparison of the 5-Minute Forecast with or without Moving Average

4 基于灰色二次回归的轴温预测模型

通过将二次多项式模型融合到GM（1，1）模型当中进行模型重构，进而得到基于灰色二次回归的轴温预测模型：

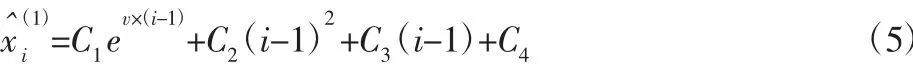
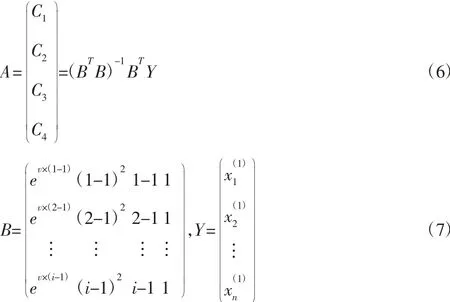
通过上述过程，即可获得基于灰色二次回归的轴温预测模型，利用该模型进行轴温预测的步骤，如图2 所示。

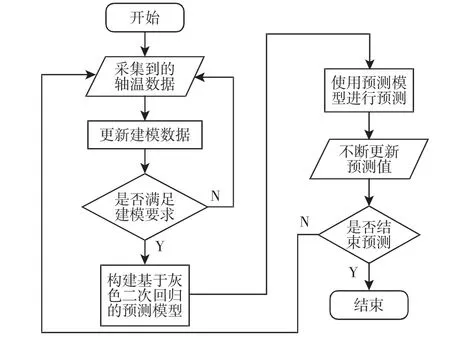
图2 基于灰色二次回归的轴温预测模型预测流程Fig.2 Forecasting Process of Prediction Model of Axle Temperature Based on Grey Quadratic Regression

5 实例验证

以某高速列车轴温数据为例，对提出的基于灰色二次回归的轴温预测模型的有效性及优越性进行验证。数据来源为某高速列车车载轴温监测系统所测得的温度数据，温度传感器为PT100，采样频率为1/60Hz，监测数据每分钟传输一次。每节车厢包含4 根车轴，每根车轴测点安装有一组温度传感器，拖车车轴测点在左右两端的轴箱上安装轴箱温度传感器，动车车轴测点在车轴及其传动链上安装了9 个温度传感器。以动车的1 轴为例，具体位置，如表1 所示。

表1 动车1 轴各温度传感器通道位置Tab.1 The Position of Temperature Sensor on Axis 1

在进行轴温预测时，建模点个数选取的不同会影响到预测模型的预测精度，数量过少会使得预测模型无法捕捉到轴温变化的总体趋势，数量过多则会使得预测模型侧重陈旧信息，进而无法充分使用新数据所包含的趋势信息。根据实验，采用当前时刻前序连续8 分钟（8 个点）的数据作为建模样本，来预测当前时刻后序5 分钟（5 个点）的轴温，并将预测值与实际值进行比较。下面通过三种典型轴温变化趋势来验证所建立的基于灰色二次回归的轴温预测模型的可行性与优越性。

5.1 轴温先升后降样本的测试结果

以1 轴小齿轮箱电机侧通道（通道9）的数据为例，分别使用GM（1，1）模型及模型进行预测，预测结果，如图3 所示。误差分布，如图4 所示。误差统计，如表2 所示。结果显示模型相比于GM（1，1）模型，最大绝对误差降低了1.95℃，同比下降了24.62%；平均绝对误差降低了1.12℃，同比下降了31.55%；误差分布更为集中且误差值较小。

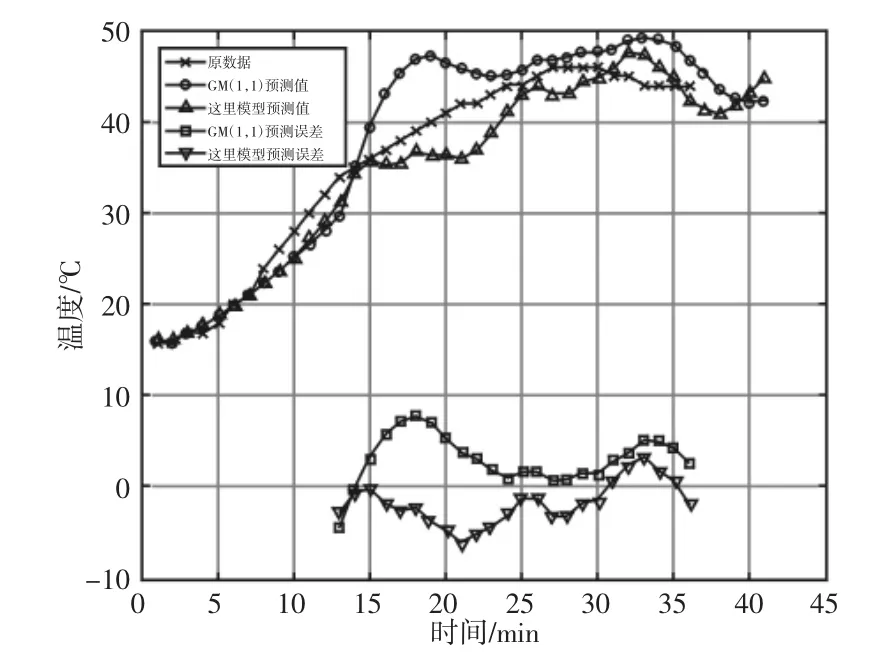
图3 轴温先升后降预测结果对比Fig.3 Comparison of Results to Axis Temperature First Rise and then Decline

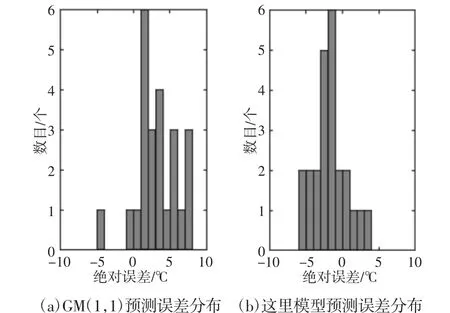
图4 轴温先升后降预测结果误差分布对比Fig.4 Comparison of Error Distribution to Axis Temperature First Rise and then Decline

表2 轴温先升后降预测结果对比Tab.2 Comparison of Results to Axis Temperature First Rise and then Decline

5.2 轴温先降后升样本的测试结果

以1 轴小齿轮箱电机侧通道（通道9）的数据为例，分别使用GM（1，1）模型及模型进行预测，预测结果，如图5 所示。误差分布，如图6 所示。误差统计，如表3 所示。结果显示模型相比于GM（1，1）模型，最大绝对误差降低了1.52℃，同比下降了26.21%；平均绝对误差降低了0.15℃，同比下降了10.49%；误差分布更为集中且误差值较小。

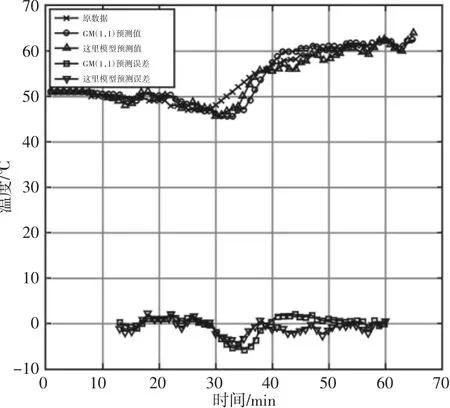
图5 轴温先降后升预测结果对比Fig.5 Comparison of Results to Axis Temperature First Decline and then Rise

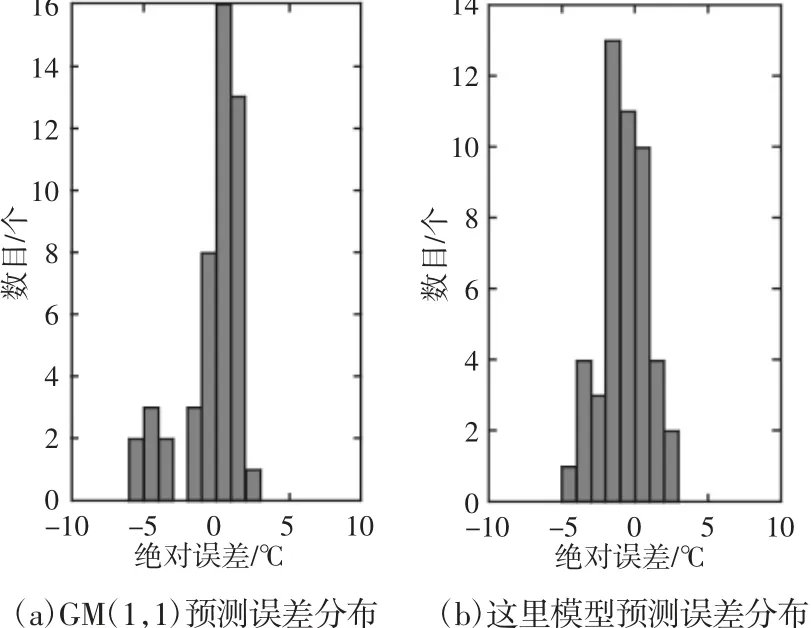
图6 轴温先降后升预测结果误差分布对比Fig.6 Comparison of Error Distribution to Axis Temperature First Decline and then Rise

表3 轴温先降后升预测结果对比Tab.3 Comparison of Results to Axis Temperature First Decline and then Rise

5.3 轴温连续波动样本的测试结果

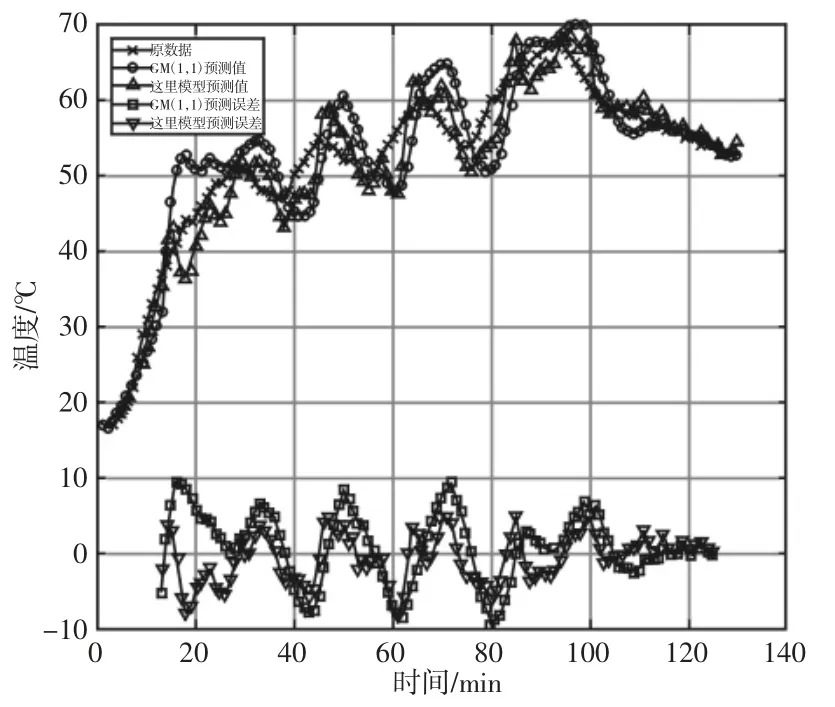
图7 轴温上下波动预测结果对比Fig.7 Comparison of Results to Fluctuations of Temperature

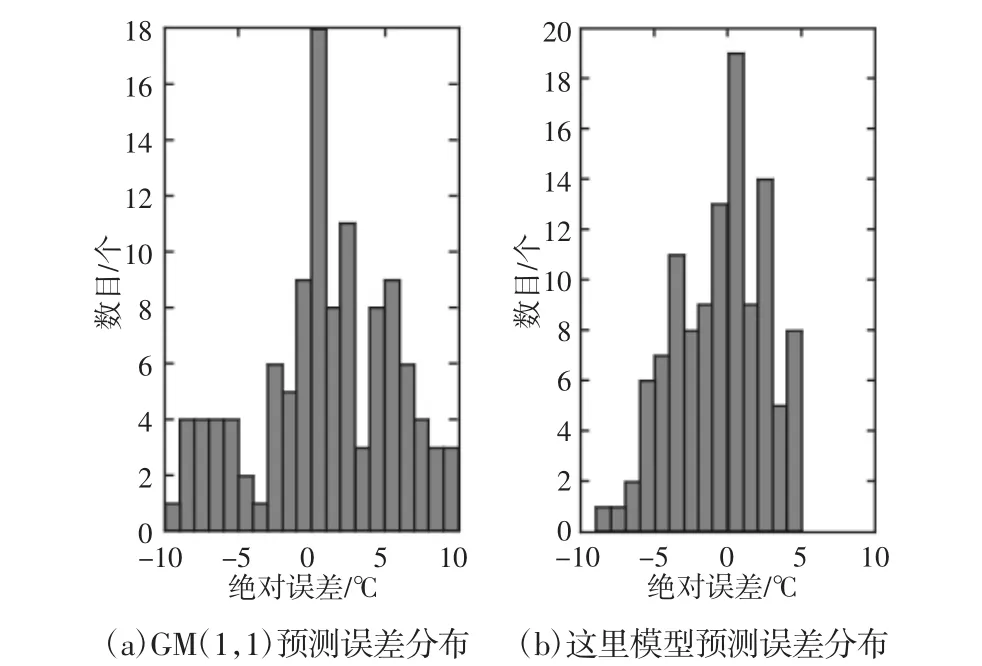
图8 轴温上下波动预测结果误差分布对比Fig.8 Comparison of Error Distribution to Fluctuations of Temperature

表4 轴温上下波动预测结果对比Tab.4 Comparison of Results to Fluctuations of Temperature

以1 轴大齿轮箱电机侧通道（通道29）的数据为例，分别使用GM（1，1）模型及模型进行预测，预测结果，如图7 所示。误差分布，如图8 所示。误差统计，如表4 所示。结果显示模型相比于GM（1，1）模型，最大绝对误差降低了1.25℃，同比下降了13.17%；平均绝对误差降低了1.23℃，同比下降了32.63%；误差分布更为集中且误差值较小。

5.4 轴温连续波动不同通道测试结果

以动车1 轴各温度传感器数据为测试样本，分别使用模型和GM（1，1）模型进行预测，预测结果对比，如表5 所示。结果表明在所有通道类型下，模型的预测结果均好于GM（1，1）模型。

表5 1 轴各通道类型预测结果对比Tab.5 Comparison of Results to Each Channel Type of 1st Axle

6 结论

以GM（1，1）模型为基础，通过对所采集的离散整型轴温数据进行迭代三次平滑处理，提高了建模样本数据的平滑性，再将二次多项式与GM（1，1）模型进行融合重构，获得一种基于灰色二次回归的轴温预测模型。基于三种典型轴温数据样本，通过对比模型和GM（1，1）模型的预测精度，验证了方法的有效性，并得出以下结论：（1）用于建模的轴温样本数据经过滑动平均处理三次后，有效提高了的模型预测精度；（2）所构建的模型相比GM（1，1）模型，提高了轴温升降趋势变化拐点处的预测精度，且在所有通道的预测结果中都得到体现；（3）在测试实例中，所构建模型相比GM（1，1）模型，其预测误差分布更为集中且误差值更小；在轴温先升后降的样本中，最大绝对误差降低了1.95℃，同比下降了24.62%，平均绝对误差降低了1.12℃，同比下降了31.55%；在轴温先降后升的样本中，最大绝对误差降低了1.52℃，同比下降了26.21%，平均绝对误差降低了0.15℃，同比下降了10.49%；在轴温连续波动的样本中，最大绝对误差降低了1.25℃，同比下降了13.17%，平均绝对误差降低了1.23℃，同比下降了32.63%；在不同通道类型的连续波动样本中，模型的预测结果均好于GM（1，1）模型，验证了模型的通用性。