积分上限函数的求导方法及其应用——以一道考研试题的解法和拓展为例

陈亚

（安阳师范学院，河南安阳 455000）

每年的研究生入学数学考试中，积分上限函数是一个必考的知识点，积分上限函数难度系数不算很高，但学生在求解过程中的计算步骤较多，中间有任何一步计算错误就会得出错误结论，近几年的考试题目在传统题型的基础上不断加大难度，出现了跟课本上不一样的类型，其目的还是考查学生对积分上限函数的概念是否理解，学生做题过程中经常死搬硬套课本上的求导方法，结果导致计算错误，本质上还是对积分上限函数理解不到位，下面以一道考研题目为例，对积分上限函数常见的题目类型进行分析，并给出通用的解题方法及思路。

2017年考研数学三第15 题是一道简答题，题目如下：

1 题目分析

这道题目本质是求极限问题，分子分母均趋向0，属于不定型，符合洛必达法则使用条件，所以可以使用洛必达法则进行求解，求解过程中，需要涉及积分上限函数求导问题，在经济数学教材中对积分上限函数给出了3 种情形，它们分别如下。

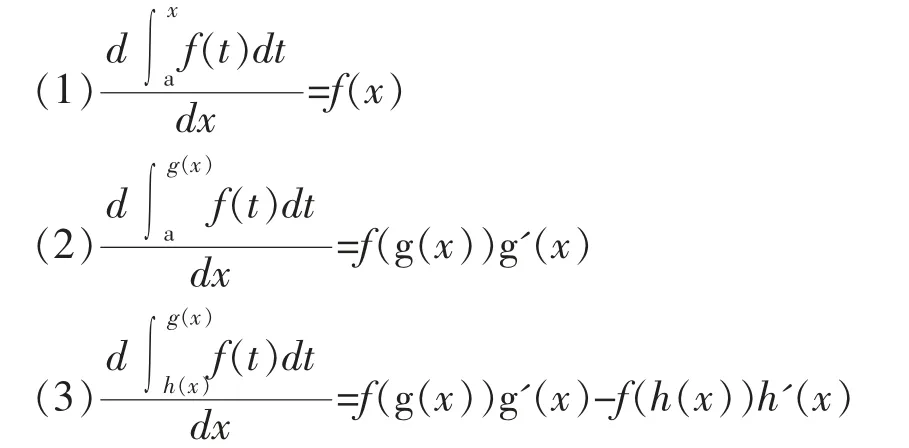
这3 种情形是最为常见的情形，它们的共同之处就是被积函数只包含形参，不含有f（x）的项，若碰到积分里面含有f（x）的项，则上述公式就失效，如果硬套用公式，就会得出的错误结论[1-3]。 被积函数里含有f（x）的的积分上限统称为含参积分上限函数，对于这类函数的求导最常见的方法是通过变换将含x 的项分离出来，分离之后再利用求导法则进行求解。

2 题目解法

解法1：将含x 的项分离出来，将之转化为常见场景：

经过变换，上述式子已经完全转化为普通的积分上限函数，因此可以同基本求导公式进行计算。按照洛必达法则，原式

解法2：

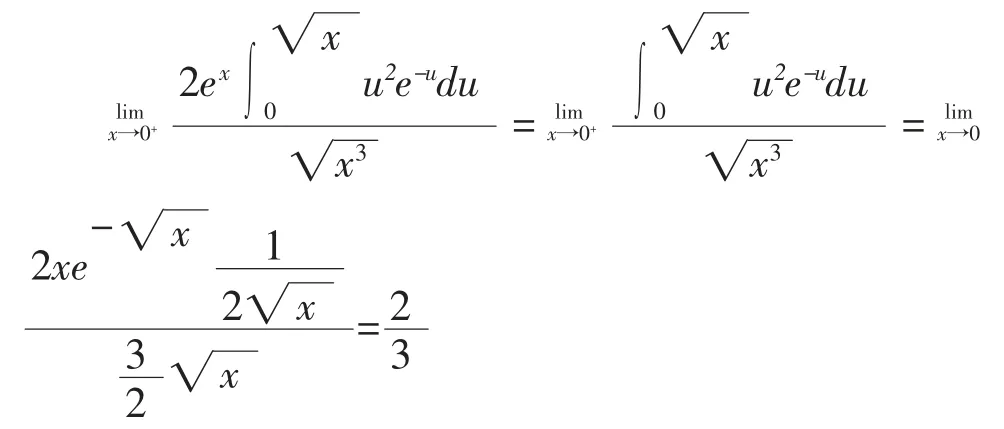
3 问题总结与拓展

一般来讲，大多数含参积分函数可以通过换元积分法将含的项独立出来，独立出来之后函数就变换为常见的3 种场景，然后可以根据教材上的求导方法进行求导，那对于一般的含参积分有没有通用的求导方法呢？

我们有如下定理：

此定理没有采用分离变量的办法，而是将函数分离成两个函数，分离之后问题就转化为一个f（x）和一个含参积分上限函数，问题就有可能转化为上述常见的3 种情形，从而问题得到解决。按照这个定理，我们就可以对一些含参积分上限函数进行求解，下面以几道例题进行分析。

4 应用实例

即f（x）为减函数，且f（1）=0，故0＜x＜1 时，f（x）＞f（1）=0，当x＞1 时，f（x）＜f（1）=1，综上，f（x）＞0 成立的取值范围为0＜x＜1。

思路分析： 不等式常见的方法有做差法和比商法，此题目采取做差的办法，构造出一个新的函数，对新函数进行求导分析，确定其增减性，根据增减性解决问题。

分析：f（x）表达式是隐性的，无法直接通过积分得出具体表达式，但f'（x）可以通过求导公式表达出来，因此符合分部积分法的特征，可以利用分部积分法进行求解。

例4：设函数f（x），g（x）在区间[a，b]上连续，且f（x）单调增加，0≤g（x）≤1，证明：

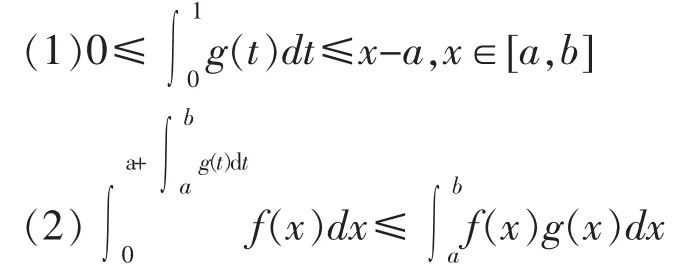
分析：第一问是积分估值不等式的直接应用，较为简单，第二问可通过构造函数（a）=0，然后结合函数求极值的方法进行解决。

证明：（1）∵x∈[a，b]，g（x）在[a，x]上连续，0≤g（x）≤1，由估值不等式

此题目为含参积分上限函数，令F（x，t）=sin（x-t）2按照拓展定理，令，代入可得：

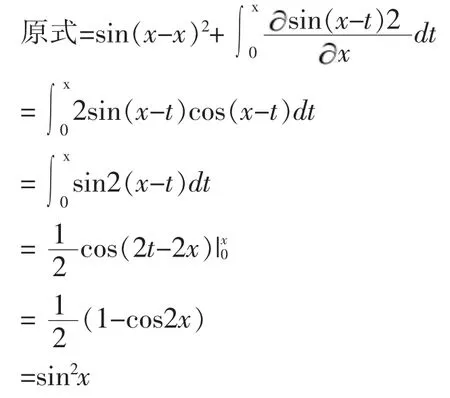
思路分析：此题目直接应用定理，将求导转化为积分，积分函数为三角函数易于求解[7-9]。也可采用变量替换的方法求解，难度基本一致。

5 结语

积分上限函数在考研题目属于高频题型，在很多数学教材上，仅仅针对3 种常见的情形进行了说明，对于含参积分上限函数的求导问题学生往往束手无策，该文通过一道考研题目的分析，给出了含参积分上限函数的常见解法，并针对一些常见题目做了应用分析，在考试中学生可结合洛必达求导法则、分部积分法、常微分方程求解等知识点，分析题目难点，充分理解积分上限函数的意义，掌握常见的求导方法，则在实际应用中就能得心应手。