泥沙吸附重金属污染物的数值模拟研究
胡新启 程凯 周晓泉


摘 要:为研究分相模型中泥沙颗粒吸附重金属的过程,以Langmuir等温式为基础,将泥沙相和重金属相看作两相,通过步进法和UDS方法两种计算方法对泥沙颗粒的吸附过程进行了数值模拟。首先利用Fluent软件将组分输运模型与UDS法相结合,模拟了7种湍流模型下的泥沙吸附过程,所得结果与Langmuir模型对比,验证了该方法的可行性,并选出了吻合度最高的模型。其次,应用选出的模型对不同含沙量、不同粒径泥沙颗粒吸附量和镉离子水相浓度变化趋势进行了模拟。结果表明:含沙量直接影响水体的吸附作用,含沙量越小,吸附作用越弱,吸附速率越慢,浓度小于一定限度时水体吸附作用可忽略不计;不同粒径泥沙在水体中的吸附作用差异明显,但并不能决定泥沙吸附量;UDS方法和步进方法在考虑粒径的影响时计算的吸附量不同,从吸附量的角度来看UDS法更加贴切,从到达动态平衡的角度来看步进法更加吻合。
关键词:泥沙颗粒;吸附;重金属;湍流模型;Fluent;UDS;步进法
中图分类号:TV142 文献标志码:A
doi:10.3969/j.issn.1000-1379.2020.05.019
Abstract:In order to study the heavy metal pollutant adsorption of sediment under the phase-separation model, based on the Langmuir isothermal equation, the sediment and heavy metal phases were regarded as two phases and the adsorption process was numerically simulated through two calculation methods: time-step method and UDS method. Firstly, the sediment adsorption process under seven turbulence models was simulated by combining component transport model with UDF using commercial software fluent. The results were compared with the Langmuir model, the feasibility of the method was verified and the model with the highest consistency was selected. Secondly, the adsorption capacity of sediment particles under different sediment concentration and particle size were obtained by using the selected model. And the change trend of cadmium ion concentration in aqueous phase was simulated. The results show that the sediment concentration directly affects the adsorption of water, the smaller the concentration, the weaker the adsorption, the slower the adsorption rate is, the less the concentration is and the less the adsorption can be. The adsorption effect of sediment particle size in water is obvious, but it cannot determine the amount of sediment adsorption. Both UDS and time-step methods have advantages and disadvantages in calculating the adsorption amount under the influence of particle size. The results of the dynamic time obtained by the stepwise method are more appropriate and the numerical results of the adsorption amount obtained by the time-step method are in better agreement with each other.
Key words: sediment particles; absorption; heavy metal; turbulent model; Fluent; UDS; time-step method
水環境污染一直以来都是备受人们关注的问题。目前,国内外大多数水域都存在不同程度上的污染,其中危害最大的便是重金属和难降解的有毒无机物[1],由于重金属离子在天然水体中具有易富集、难降解、可通过食物链进行转移等特点,因此受到越来越多学者的重点关注。前人在研究水体中的重金属离子时,发现水中的泥沙颗粒可以吸附重金属离子进行迁移转化,从而达到净化水体的目的;另一方面,当水体中的外部环境发生改变时(如水温、pH值、盐度变化),吸附在泥沙颗粒表面的重金属可能被再次释放,从而造成二次污染。为了尽可能减轻重金属对于人类生活的影响,泥沙颗粒吸附重金属规律的研究便显得十分迫切。
以往大多数学者在研究泥沙颗粒的吸附效应时,多采用物理模型试验和利用实测数据进行分析的方法[2],但是由于物理试验以及实测方法费时费力,并且泥沙吸附重金属是一个微观过程,研究结果易受外部因素干扰,因此有学者开始探索利用数值模拟方法来研究泥沙吸附重金属的规律。如:郑康[3]运用数值模拟法对水沙环境中重金属离子的迁移转化进行了初步分析,并通过算例证明了泥沙颗粒是重金属离子迁移转化的主要载体;朱蕾[4]对重金属的迁移扩散规律进行了模拟,但所得重金属浓度分布与实际情况有一定出入。前人在数值模拟方法上取得了一定成果,不过在采用数值模拟方法进行泥沙吸附重金属的研究时,大多把泥沙和重金属看作一相来表明其吸附完成过后的迁移转化规律。而在天然河流水体中,不仅存在已经吸附在泥沙颗粒上的重金属离子,也存在着溶于水中的重金属离子,所以不应简单地仅考虑泥沙颗粒的迁移转化,而要将天然河流看作一个整体来进行分析。因此,本文将泥沙颗粒和重金属离子(以镉为例)看作两相,结合组分运输模型和用户自定义标量方程(User Defined Scalars,简称UDS),得出镉离子浓度在水中的变化过程,从而为研究泥沙吸附重金属的过程提供一个新思路。
1 数学模型的建立
本文主要采用Fluent软件进行泥沙吸附重金属的数值模拟,由于天然水体的水流多处于复杂的三维紊流状态,流速相对较低,且水是不可压缩流体,因此建立不可压缩黏性三维紊流的数值模型。
1.1 控制方程
1.1.1 质量守恒方程
解决流动问题首先需要满足质量守恒定律。质量守恒方程[5]为式中:cS为组分S的体积浓度;ρcS为组分S在系统中的质量浓度;DS为组分S在系统中的扩散系数;SS为系统内单位体积、单位时间化学反应所产生的组分S的质量。
1.1.3 动量守恒方程
1.2 吸附等温式
研究泥沙颗粒吸附水体中重金属污染物的问题时,通常采用Henry吸附等温式、Langmuir吸附等温式以及Freundlich吸附等温式3种吸附模型,3种模型包括了平衡吸附模式和动力学吸附模式[10]。Henry等温式建立在泥沙颗粒吸附量与污染物浓度成正比且重金属污染物浓度很低的基础上,可以描述为式中:kd和n都是常数,没有明确的物理意义。
Langmuir吸附等温式的适应情况比较广泛,通常在任何浓度条件下都可以采用。它是以单分子层吸附理论为基础推导得出的,该等温式有3个假设性条件:①吸附颗粒表面均匀,分子吸附可能性相等;②每个位置只能吸附一个分子且为单层吸附;③吸附过程是个动态平衡的过程。
由于Langmuir吸附等温式适用于任何条件,因此在泥沙颗粒吸附重金属污染物的研究中得到了广泛应用。比较上述3种吸附等温式,Langmuir吸附等温式应用更为广泛,且式中的每一项参数都有明确的物理意义,因此本文采用Langmuir吸附等温式作为吸附理论和CFD(计算流体力学)模拟的基础。
1.3 UDS法的源项
泥沙吸附重金属是个极其复杂的微观过程,仅通过Fluent软件自身所提供的模型无法很好地模拟吸附过程,因此采用C语言编程来实现对吸附过程的模拟,采用步进法和用户自定义标量方程(UDS)两种不同的求解方法进行分析对比,并将所得结果与基于Langmuir吸附等温式以及前人的试验数据[11]所得的理论吸附量进行对比。所用的两种方法均基于理论吸附量,理论吸附量通过Langmuir吸附等温式并结合试验数据计算得到。
2 计算模型
2.1 几何模型及网格划分
本文采用的几何模型思路来自杨美卿、钱宁的研究成果[12]。受数值模拟的限制,对模型进行了部分类比转化,建立的几何模型见图1,为一内置旋桨的圆筒,通过给旋桨一定的转速以达到混合筒中水沙的目的。采用多坐标系的方法建立三维非定常数学模型,将模型划分为3部分:顶部段、旋转段以及底部段。使用非结构化四面体网格划分模型,对旋转段进行了网格的局部加密,计算区域共设置60 840個网格单元。不同部分接触面之间设置为INTERIOR,计算网格见图2。
2.2 初始条件及模型参数
本文所用的初始参数均来自前人试验[9],水体中的组分有3种:泥沙颗粒、镉离子以及水。由于初始时的镉离子溶解于水中,其基本物理参数设置与水相同。各组分物理特性见表1。Langmuir方程参数参照设置分别为:吸附速率K1=9 m3/(kg·s),解吸速率K2=0.001 08 1/s,饱和吸附量B=0.000 767 kg/kg。
3 模型验证
3.1 流场模拟
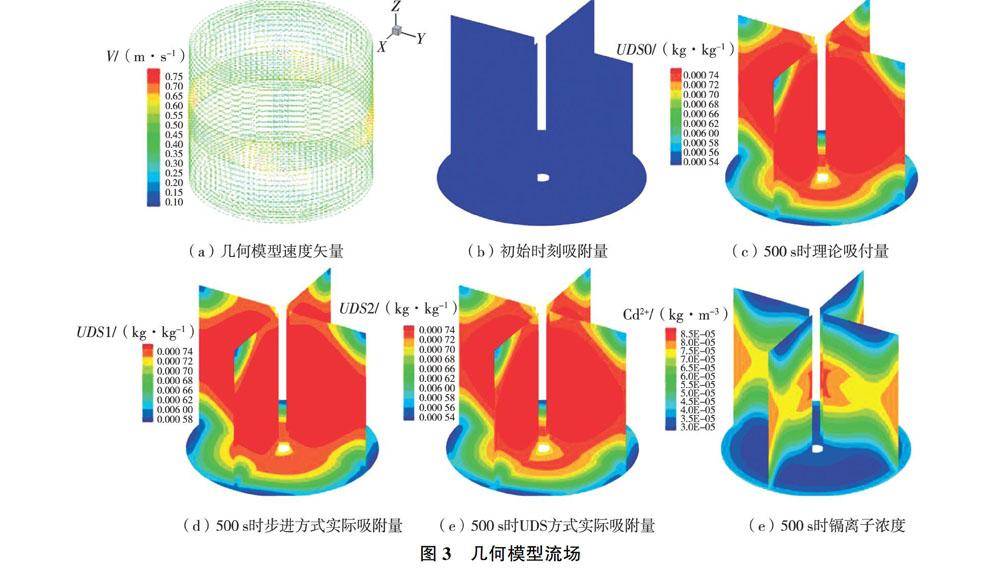
仅选取Reynolds Stress湍流模型(简称RSM)流场作为研究对象来对流场模拟结果进行分析。几何模型速度矢量图及流场模拟结果见图3。由图3可知,旋桨所在位置水流流速最大,并带动上下水流同时运动,顶部段的流速与底部段的流速在数值大小上关于旋桨对称;初始时刻水体中并未产生吸附作用,因此其理论吸附量数值为0,随着时间延长,模型内部发生吸附现象,500 s时UDS方法计算结果与理论吸附量基本相等,而与步进法的计算结果有一定差异。几何模型的吸附量最大值处于旋桨及其附近区域,在这一区域水流流速较大且掺混剧烈,因此镉离子吸附量最大,外层水流紊动逐渐减弱,因此吸附量开始逐渐减小。镉离子则主要集中在中间的旋转段,随着与旋转段距离的增大而逐渐减小,这一趋势同镉离子吸附量的趋势一致。计算结果与实际情况符合,因此可认为本文所采用的计算模型具有实用性。
3.2 7种不同湍流模型对比
Fluent软件中提供了多种湍流模型,但是实际工程中并没有一种湍流模型可以完全适用于所有的流动,每种湍流模型都有一定的适用范围。因此,本文使用7种不同的湍流模型进行验证,以找到最适用的湍流模型。
由于Langmuir模型在各种浓度条件下都可用于吸附量的计算,并且前人通过这一模型进行过众多关于吸附作用的试验研究,认为Langmuir模型能较好地描述试验结果,因此本文选用Langmuir模型来对不同湍流模型的计算结果进行验证,从而选出与实际情况吻合程度最高的湍流模型。Langmiur模型见图4。
图5为7种湍流模型的吸附量与镉离子水相浓度统计情况,整体来看,各湍流模型不同方式吸附量的变化趋势与Langmuir模型的基本相同,因此认为本文采取的数值模拟方法可以用来描述泥沙颗粒对重金属离子的吸附过程。同时,虽然不同湍流模型的吸附量变化的基本趋势类似,但是计算结果仍然存在一定差异。由图5(a)中Ke-RNG曲线可以看出,RNG k-ε模型的最终水相浓度远低于其他湍流模型的,且镉离子浓度的减少量与泥沙颗粒的吸附量并不相同,其计算结果可能存在较大误差;由图5(b)、(c)、(d)中Ko-std以及Ko-SST曲线可以看出,在k-ω模型中,泥沙颗粒的吸附量变化速率出现了先增大至一定点后保持不变,然后继续增大的趋势。本文在旋转模型中进行模拟,模拟中途并未增加其他变化情况,其吸附速率的变化应为一个连续过程而并不会出现k-ω模型曲线中的拐点,因此k-ω模型不适用于本文的模拟条件。在其他湍流模型中,无论是吸附量与镉离子在水相浓度中的对比还是其吸附速率与时间的变化趋势,RSM模型都能较好地满足Langmuir模型与试验数据,因此本文在下面的研究中选用RSM模型。
4 泥沙吸附重金属的数值模拟
4.1 含沙量的影响
为研究不同的含沙量对重金属离子吸附的影响,在离子浓度为2 mg/L的情况下,选取0.000 9、0.000 7、0.000 5、0.009、0.007、0.005、0.003、0.001、0.03、0.01 kg/m3共10种含沙量进行泥沙吸附重金属的数值模拟计算,结果见图6。由图6可以看出:随着含沙量增大,水体吸附作用增强,吸附速率加快,吸附量增大。当含沙量小于一定限度时,泥沙颗粒的吸附量差距不大,可以忽略不计。同时也可以看到,随着初始含沙量增大,吸附达到动态平衡所需的时间缩短。
10种含沙量的理论吸附量计算结果完全相同。理论吸附量的计算结果是通过公式计算得到的,含沙量并不影响计算结果。
初始时刻含沙量不同时,两种方式的计算结果基本相同,都符合Langmuir模型,不存在较大波动。当镉离子浓度相同时,不同含沙量的吸附量计算结果相同,其原因为在一定镉离子浓度下,水体中的泥沙颗粒吸附量存在最大值,无论含沙量如何改变,其吸附量只能达到一定的限值,也即含沙量的大小并不会影响吸附等温式的参数,当吸附量达到该数值以后,吸附速率与解吸速率始终保持平衡,不会随着含沙量变化而改变。
4.2 泥沙粒径的影响
为研究不同粒径泥沙颗粒对镉离子的吸附作用,选取4组不同粒径的泥沙分别进行计算,泥沙颗粒参数见表2,计算结果见图7。理论吸附量的计算结果取决于Langmuir吸附等温式与试验所测数据,不同粒径泥沙颗粒的分组中,公式所用的参数也不相同,因此计算所得的理论吸附量存在较大差距。由吸附量计算结果可知,不同粒径泥沙颗粒分组下,镉离子的水相浓度以及泥沙颗粒的吸附量均存在较大差异,泥沙粒径的大小并不会直接决定吸附量的多少。造成这一现象的主要原因:泥沙颗粒吸附重金属时,存在物理反应和化学反应两种情况,物理反应主要取决于泥沙颗粒的表面形貌,而化学反应则取决于泥沙颗粒表面的活性组分,因此泥沙粒径的大小并不能够决定吸附量的多少。同时,观察吸附量计算结果可以看到两种不同的计算方法所得的结果有一定出入。步进法计算结果的吸附过程与理论吸附过程的拟合程度更高,但是在最终吸附量的计算结果上与理论吸附量有一定的差距,UDS方法在吸附过程的模拟上不如步进方法准确,但是在最终吸附量的计算结果上更加接近理论吸附量的计算结果。因此,在考虑泥沙粒径对吸附过程的影响时,本文所采用的两种方法都存在一定缺陷,需要将两种方法的计算结果结合起来进行分析,不能够单一而论。
5 结 语
(1)前人的研究大多把泥沙颗粒与重金属离子看作一相,重点研究泥沙颗粒吸附重金属离子后的迁移转化过程。本文使用Fluent软件,将泥沙颗粒和镉离子看作两相,研究其吸附过程,为使用数值模拟方法研究泥沙吸附作用提供了新的思路。
(2)使用7种不同的湍流模型对选用的方法进行验证,结果表明各湍流模型都能较好地模拟泥沙颗粒与镉离子之间吸附作用的变化趋势,因此本文所选的方法具有实用性。但是,不同湍流模型的吸附量之间存在一定差异,RSM模型相对于其他湍流模型的吻合程度最好。
(3)步进法和UDS法所得的计算结果基本相同,其中UDS法所得的计算结果与理论吸附量吻合程度更高。
(4)对不同含沙量下的泥沙颗粒吸附重金属过程进行了模拟,在其他条件相同的情况下,随着含沙量的增大,泥沙颗粒与重金属离子的吸附作用增强,吸附速率加快,吸附量增大。
(5)研究不同泥沙粒径对于吸附过程的影響中发现,本文所提出的两种计算方法相对于理论吸附量都有一定差别。从吸附量的角度来看,UDS法更加贴切;从到达动态平衡的角度来看,步进法更加吻合。
参考文献:
[1] 路瑞利,李彬,高柯,等.河流水体污染与泥沙环境效应研究进展[J].人民黄河,2010,32(4):77-78.
[2] 黄岁梁,万兆惠.河流泥沙吸附-解吸重金属污染物试验研究现状(一)[J].水利水电科技进展,1995,2(2):28-32.
[3] 郑康.水沙环境中重金属迁移转化数学模型初探[D].天津:天津大学,2008:45-46.
[4] 朱蕾.重金属迁移的实验及数值模拟[D].天津:天津大学,2010:46-47.
[5] VEERSTEG H K, MALALASEKERA W. An Introduction to Computational Fluid Dynamics: The Finite Volume Method[J]. Pearson Schweiz Ag., 1995, 20(5): 400.
[6] 王福军.计算流体动力学分析[M].北京:清华大学出版社,2004:24.
[7] 彭荣.多孔材料吸附储氢的CFD模拟与优化[D].武汉:武汉理工大学,2012:12.
[8] 黄岁梁,万兆惠,王兰香.泥沙吸附重金属污染物室内静态试验研究[J].水科学进展,1994,5(4):271-279.
[9] 黄岁梁,万兆惠,王兰香.不同粒径泥沙解吸重金属污染物静态试验研究[J].水动力学研究与进展,1995(2):204-213.
[10] 李然,李嘉,赵文谦.水环境中重金属污染研究概述[J].四川环境,1997,16(1):18-22.
[11] 黄岁梁,万兆惠,张朝阳,等.泥沙粒径对重金属污染物吸附影响的研究[J].水利学报,1994,25(10):53-59.
[12] 杨美卿,钱宁.紊动对细泥沙浆液絮凝结构的影响[J].水利学报,1986,17(8):23-32.
【责任编辑 翟戌亮】

