应用多层圆筒热传递改进模型的高温作业服设计

赵紫曼 路标 于哲苏

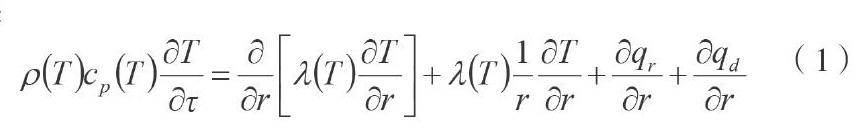
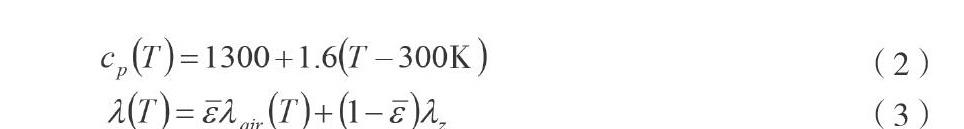
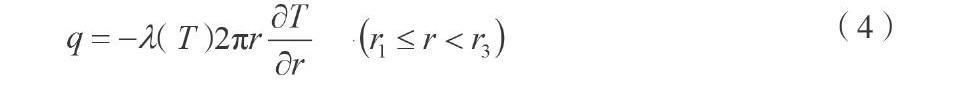
摘  要：高温作业服可以有效避免灼伤，并在实际作业中得到广泛应用，其一般由3层及以上的不同材料合成。该文就高温服材料的厚度优化问题进行研究，将人体近似看成圆柱体，作业服则为多层圆筒建立非稳态导热模型，利用傅里叶定律、牛顿冷却公式、能量守恒定律，结合边界条件和初始条件，分析了在高温条件下不同厚度作业服的温度随时间变化的分布状况。得到了在人体皮肤所能接受的温度条件下，合适的织物厚度、织物与人体之间的空气层厚度以及人体在高温条件下所能暴露时间的极值。这对于人员的安全以及防护服制作都有着重大意义。最后对该文所使用的模型进行了综合评价。

关键词：多层圆筒导热模型;高温防护服;非稳态一维传热;微元分离变量

中图分类号：TS941            文献标志码：A

1 问题假设

由于人体和防护服均属于不规则三维几何体，不能直接建立“外界-服装-空气层-皮肤”的三维非稳态温度场分布模型，因此我们假定人体受热部分近似为圆柱体，因为人体散热比较均匀，所以为了更接近实际情形，我们假定传热过程只沿一维径向（垂直于皮肤表面）进行，且只考虑对流和传导。

2 模型建立

2.1 单层圆筒壁模型

图1为一维热传递过程。在计算过程中，因为人体受热是均匀的，所以我们可以将圆柱体分成若干微元体进行分析[1]。

假设服饰织物为灰体，我们可以得出单层织物的传热模型：

2.2 非稳态传递模型的2个定解条件

2.2.1 初始条件

热防护服在刚进入高温环境中时间t=0时的温度T（r，0）已知，假设最外层织物的半径为r1，在高温强对流的作用下，此时几乎没有热量耗散，织物最外层温度就相当于外界温度，即

2.2.2 边界条件

假设防护服由3层不同的材料组成，即最外层（半径r3），中间层（半径r2）和内层（半径r1）。基于假设中间层与内层可以近似看成只存在热传导[3]，由此可以写出在任意时刻织物左边界的热流密度q的分布函数：

2.3 模型的求解

設圆筒型的“外界-三层织物-空气层-皮肤”的温度分布函数为θ（r，t）。

式中：。代入边界条件得到为方程的根。a为热扩散率，为温度对半径的偏导，U、W、V、S查《热传导理论》可得[2]。最后我们将θ（r，t）函数输入Fluent软件中，并设定环境温度为75 ℃、I层厚度为0.6 mm，II层厚度为6 mm、III层厚度为3.6 mm、空气层厚度为5 mm，在工作时间为90 min的情况下，对实验的相应参数进行观察，得到的温度分布图像大致如图2所示。

3 模型测评

3.1 织物层厚度与温度分布关系

我们发现随着厚度的增加，人体可暴露的安全时间就越长，但太厚的织物不宜穿戴，而且热量不易散失，停留在皮肤表面的时间会增加。从织物层厚度的温度变化曲线可知，第二层两端的温差最小，其对最大温度的影响最小。放在最不利的温度变化条件中，我们使中间层厚度满足约束条件。设定不同厚度的中间层，并列出温度与时间的约束条件，并得到曲线图3。

3.2 结果分析

从图线中可以看出5点。1）皮肤外层与厚度r满足非线性单调递减关系。2）不同厚度对于趋近于稳态的最大温度影响不大。3）随着厚度的增加，调节时间（达到稳态的收敛时间）不断增大。4）当厚度增加到一定值后，趋近于稳态的最大温度会明显降低——意味着衣物的重量与笨拙度增加，不符合舒适与经济性能指标。5）最后考虑到舒适性、经济性、性能稳定性与安全性要求，得到中间层厚度在12 mm～16  mm较为合适，且可以在皮肤暴露时间>50 min的状态下保持稳定。

3.3 空气层厚度与温度分布关系

通过计算过程分析可得，没有空气层比存在空气层时，温度上升速率更快，所以空气层是较为理想的绝热体，在防护服的加工过程中，可以增大织物层之间的缝隙，以此来保护人体皮肤。

4 结论

结合实际情况以及优化目标建立相应约束条件后，得到基于模型的温度分布情况，使用Fluent对中间层厚度与温度变化的模型进行模拟，得到织物的最优厚度为16 mm～20 mm。并对模型进行了检验，证明多层圆筒温度分布模型较为准确，可以推广至其他热传递相关的问题，例如保温杯的材料层厚度设计等问题。

参考文献

[1]朱方龙.服装的热防护功能[M].北京：中国纺织出版社，2015.

[2]胡汉平.热传导理论[M].北京：中国科学技术大学出版社，2010.

[3]卢琳珍.多层热防护服装的热传递模型及参数最优决定[D].杭州：浙江理工大学，2018.