基于机器学习和动力学模型的湖北省新型冠状病毒肺炎疫情分析

余锦芬，宋玉凯，费菲，孙卫强，宋祖峰

(1.华中科技大学同济医学院附属湖北妇幼保健院，武汉 430070；2.电子科技大学格拉斯哥学院，成都 611731；3.中冶南方工程技术有限公司，武汉 430223)

1 引 言

2020年1月，新型冠状病毒肺炎(COVID-19)疫情在我国境内爆发。如今，在全体国人的共同努力下，疫情已经得到基本控制。在此，我们基于湖北省武汉市武昌方舱医院轻症患者的数据和其他官方数据，利用机器学习、回溯传播模型、抽样检测模型、SIR及SIER动力学模型、元胞自动机模型等工具对湖北省的此次疫情进行复盘，以总结出在未来如何更好地应对类似突发疫情的宝贵经验。

2 机器学习拟合

在收集了官方数据后，以2019年12月8日武汉第一次发现感染者为起点，对数据进行机器学习拟合[1]。由于文章篇幅限制，在此仅讨论时间和死亡病例数量之间的函数关系。

假设死亡人数与经过天数的函数关系为：

hθ(t(i))=θTt=θ0+θ1t+θ2t2

(1)

其中，hθ(t(i))代表假设的函数关系，t代表经过的天数，θT，θ0，θ1，θ2代表拟合的参数。则此函数的代价函数为：

(2)

其中，D为实际的死亡人数，m是数据集中数据的个数，在此取得2020年1月25日至2月11日(对应为第49天至第66天)共18个数据，即m=18。接着对代价函数的参数θj求偏导可得：

(3)

经过推导可得最终的每轮参数更新算法为：

(4)

其中，α为学习率，此处取α=0.01，轮数设为400轮，MATLAB拟合后得到误差曲线，见图1。

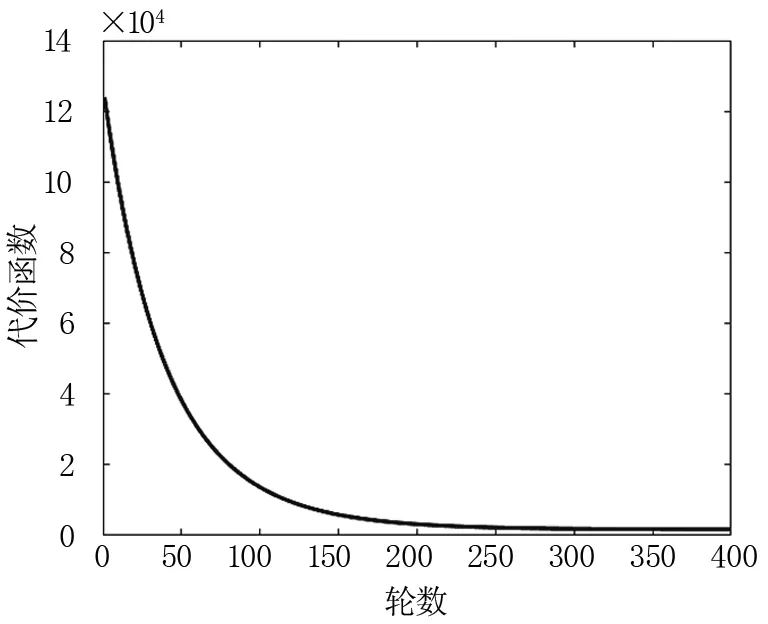
图1 代价函数与轮数的关系曲线

经过400轮学习后，最终得到的参数是θ0=5420，θ1=-231.9，θ2=2.492。该拟合函数相比较实际数据，相关系数R2≈0.99，高于一般统计学所规定的显著性水平(0.95)。由于早期数据的缺失，则只对第49天至第66天(2020年1月25日至2月11日)的数据进行了比较，见图2。

3 回溯传播模型

回溯传播模型主要是借鉴了英国帝国理工学院的成果，同时对其中的一些参数进行了更新[2]。我们做出如下假设：

(1)境外国家和地区对来自武汉的游客增设入境筛查，检验工作始于2020年1月15日，且武汉的游客随机均匀分布在离境和未离境人口中。

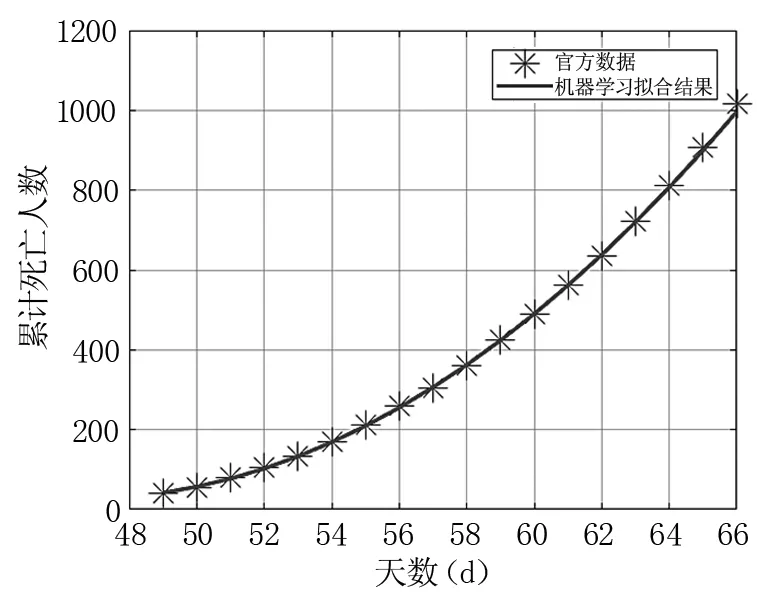
图2 机器学习拟合结果与官方数据的比较

(2)由武汉至境外的COVID-19患者均可被确诊。

(3)武汉天河机场的吞吐量为每年2 715.2万游客。

(4)COVID-19患者从感染到就医之间的间隔时间平均为T=10 d[3-4]。

(5)从武汉天河机场出发进行国际旅游的游客数量为n2=3 301/d。

(6)武汉天河机场覆盖的总人口，即武汉市的总人口为N2=1 400万。

将武汉感染COVID-19总人数设为N1,其中境外确诊的病例数为n1，则任一从武汉出境人员在目的地被确诊患病的概率p为：

(5)

而概率p也可由平均潜伏期内武汉市人口出境比例给出：

(6)

其中，n2为武汉天河机场每天出境的人数，N2为武汉市总人口，T为从感染到确诊的时间。

至2020年1月18日，境外共报告了n1=7例感染者。根据式(5)和式(6)可以推算出，武汉市1月18日感染COVID-19的总人数N1约为：

(7)

在95%的置信区间里，确诊人数范围为1 700至8 600人。同理，依据1月12日境外一共报道了3例感染者，可以推断出1月12日武汉有1 272人感染，由于早期感染者主要集中在武汉，整个湖北省的感染人数约等于武汉市的感染人数。

4 抽样检测模型

此处的估算是基于部分国家于2020年1月31日左右进行的撤侨，具体数据见表2。这里做出如下假设：

(1)在武汉的外国侨民与武汉市民充分均匀混合，感染COVID-19的概率与普通武汉市民一致。

(2)各国在撤侨行动中没有拒绝已经有发热症状的侨民登上飞机。

(3)各国侨民在1月23日武汉封城后，严格遵守了不出门的居家隔离政策，未再出现新的感染。

(3)从武汉撤回各国的侨民均得到了充分的核酸检测，做到每人排查到位。

表2 各国从武汉撤侨数据

基于各国的撤侨数据在95%的置信水平下，可估算出1月23日武汉实行封城时感染人数大致在10万至30万，平均值为19万。在疫情早期，只有核酸检测双阳才可被称做确诊，同时由于检测试剂的缺乏，导致了大量患者的漏诊，因此中南医院的专家也提出过用CT检测代替核酸检测的建议。

5 SIR模型

在上述第3节和第4节对实际感染人数估计的基础上，SIR模型被用于此次疫情进行动力学分析[5]。这个系统中包含的人群及其之间的转化关系见图3。

图3 SIR传染病模型

SIR模型可分为两个阶段：

(1)感染人群接触到易感人群后，就有可能将他们感染，数学描述为：

(8)

其中，S代表易感人群总数，t代表时间，β代表传染率，等于感染者平均每天接触到的易感人数k与密切接触易感者传染的概率b相乘，β=kb。N=S+I+R代表人群总数，现有感染人群恢复，其变化规律可表示为：

(9)

其中，γ=1/C为死亡或治愈的平均速率，取决于感染持续的平均时间C，即医学意义上的总病程。

(2)由式(8)和式(9)可推导出现有感染人群变化规律：

(10)

式(8)、式(9)和式(10)共同组成了SIR传染病动力学系统。在此基础上设感染人群的死亡率为d，则死亡数D与时间t的关系为：

D(t)=d·[N-S(t-C)],t>C

(11)

5.1 参数估计

下面是对动力学系统参数的估计。

(1)人口总数N=S+I+R取湖北省的总人口数，为5 917万人。

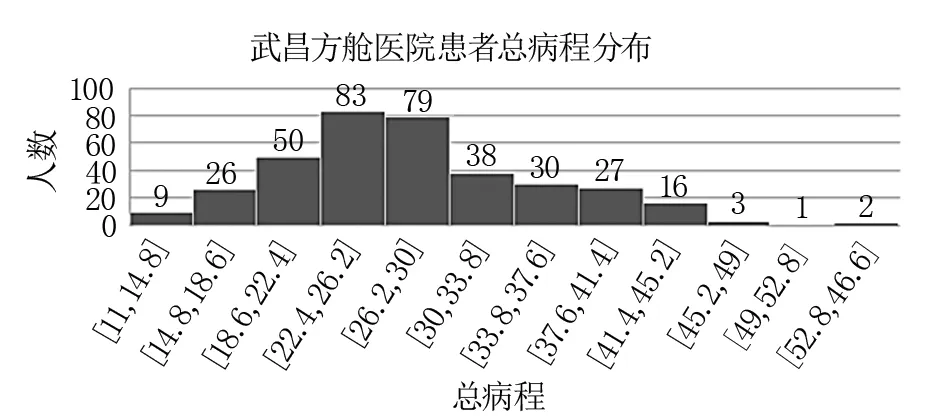
图4 武昌方舱医院患者总病程分布

(3)由官方数据可以估算感染者平均每天接触到的人数k，k的值近似等于每天密切接触者变化量/感染人数变化量，得到不封城时的k近似12， 封城后的k近似为5。

(4)由可靠的迁徙大数据工具可以得知，2020年1月23日前，武汉市总人口1 400万中的约1 200万滞留在了湖北省(其中900万在武汉市)。根据回溯传播模型的计算，可以得到表3。

表3 撤侨抽样模型估计感染人数结果

(5)根据回溯传播模型得到表4。

表4 回溯传播模型估计感染人数结果

(6)最新数据表明，湖北省的COVID-19患者死亡率为4.55%。

假设最初2019年12月8日的零号患者只有1人。在疫情早期，感染和恢复的人数相对易感人群数量均非常少，因此有：

S=N-I-R≈N

(12)

基于式(12)，式(10)可以简化为：

(13)

在前面已经预设了初始只有一位零号患者，即I(t=0)=1，则求解式(13)可得到：

I=e(kb-γ)t

(14)

而基于两个规模估算模型得到的数据，分别按照式(14)进行拟合，可以得到接触时传染的概率b分别为0.01207和0.00937，进一步对病毒的基本再生数R0进行计算：

4.07或3.16

(15)

此结果和帝国理工[6]估计的1.9～4.2是很接近的。相比之下，,埃博拉病毒的基本再生数为1.5～2.5,重症急性呼吸综合征(SARS)的基本再生数为0.85～3，甲型H1N1流感的基本再生数为1～2，由此可知，COVID-19的传染能力是很强的。

5.2 结果

从3月份的后续情况来看，R0=4.07更接近实际，所以，在此只显示R0=4.07的结果。利用MATLAB软件模拟湖北省消极防控疫情，结果见图5。

由图5可以看出，疫情将在开始后的第78天达到峰值，预计将有超过3 600万人被感染，占湖北省6 000万总人口的60%，此数据与德国、英国政府消极防控预计有60%的人将被感染的结论也相吻合。

与消极防控的西方政府不同，中国政府采取的最强有力的防控措施很快实施到位，使参数k和b均明显下降。调整了MATLAB程序的参数后，对疫情发展进行了新的模拟，结果见图6。

图5 SIR模型对政府消极防控的模拟

图6 SIR模型对政府积极防控的模拟

由图6可知，在积极防控之后，湖北省的现有感染人数峰值的出现时间从第78天提前到了第46天，说明现有感染人数的上升趋势得到了有效遏制，峰值也下降99.6%左右。

下一步是预测拐点。随着诊断技术的进步和医疗资源的逐渐丰富，检测能力明显增强，所以采用指数函数模型对政府检测的病例数进行拟合，MATLAB模拟的结果见图7。

依据官方的定义，拐点为现有确诊人数开始下降的时间点，即政府预测曲线和实际感染曲线的交汇点，之后现有确诊人数几乎会和实际感染人数的趋势相同，一起下降。依据拟合的结果可知，在第72天至第74天(2020年2月17日至2月19日)之间将会出现拐点，这与实际中2月18日出现拐点是很接近的。

6 SIER模型

基于SIR模型，我们又加入了处于潜伏期的患者人群E，引申出SEIR模型。图8和式(16)展示了此SEIR模型中不同人群的转化关系。

图7 基于SIR模型的拐点预测(拐点为两条曲线的交汇点)

(16)

依据相关信息可知，COVID-19即使在潜伏期依然具有很强的传染性，而SEIR模型的基本假设是潜伏期的患者不具备传染性，由此可知，SEIR模型对疫情的模拟效果比SIR模型要差。所以，在此仅展示SEIR模型对政府消极防控的模拟结果，见图9。

由模拟结果可知，疫情将会在第109 d达到峰值，预计约有2 500万人感染。

7 元胞自动机模型

动力学模型虽然能从宏观角度对疫情进行很细致的分析，但却难以从微观的角度对疫情发展有更细致的研究。因此，在此采用元胞自动机模型从微观角度做进一步分析。

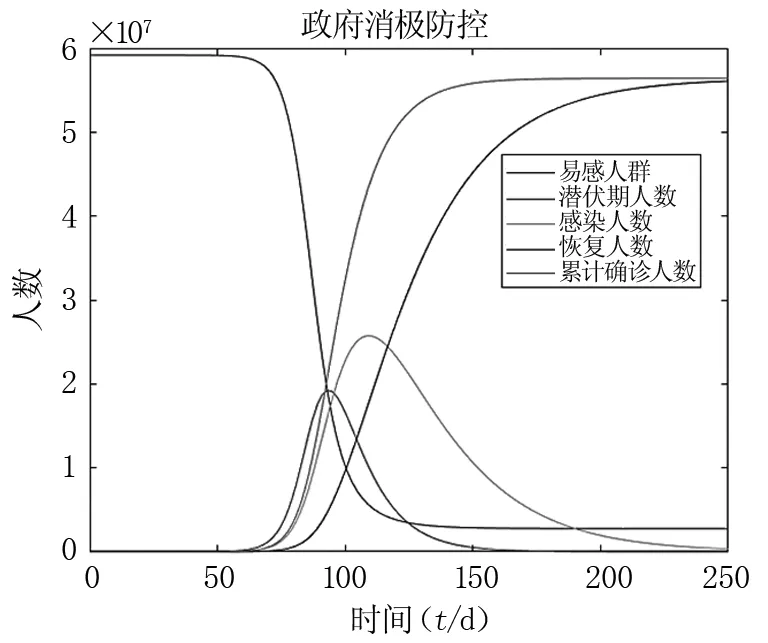
图9 SEIR模型对政府消极防控的模拟

该模型遵循以下规定：

(1)不同种类的元胞代表不同种类的人群(S元胞：易感人群,I元胞：现有感染人群,R元胞：恢复人群)。

(2)如果易感人群(S元胞)的东西南北有现有感染人群(I元胞)，则S元胞第二天将以概率Pr转化为I元胞；(1-Pr)的概率保持原状。

(3)现有I元胞经过T天后会被隔离，失去传染能力。

(4)I元胞经过C天后转为恢复人群(R元胞)。

(5)R元胞的状态不会再发生任何变化。

7.1 参数估计

恢复时间C取28.1 d，经过平均约T=11 d后，感染者去医院进行隔离，隔断传染途径。在T时间段中，现有感染者能传染给R0人，R0取4.07。因此，每天传播的概率为：

(17)

7.2 结果

首先在500×500的空间里对采取消极防控后的疫情发展进行模拟，早期的情况见图10。

由图10可知，现有感染人群(I元胞)区域迅速扩大，而早期恢复获得抗体的人数很少，无法阻止疫情的蔓延趋势；在后期，疫情将会慢慢好转，但这是以较多人群感染后死亡为代价的，见图11。

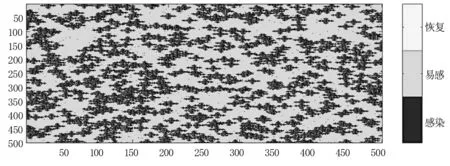
图10 元胞自动机模型对疫情早期政府消极防控的模拟

图11 元胞自动机模型对疫情后期政府消极防控的模拟

而假如从疫情开始就积极防控，则能较快抑制疫情，图12展示了积极防控疫情后的效果。可以看出，和消极防控后的疫情发展相比较，并未危及太多人群，最大可能地保护了人民群众的生命安全。

图12 元胞自动机模型对政府积极防控的模拟

8 结论

机器学习可以很好地对疫情发展进行拟合，可用于疫情数据的早期预报，以便判断疫情的严重程度，制定相应的防控措施。根据SIR模型的预测，在此次疫情中，如果政府不采取强有力的措施进行防控，湖北省将有3 600万人被感染，且疫情需到2月末才能达到顶点；而在采取了防控措施后，疫情的上涨趋势得到抑制，顶峰提前至1月出现，拐点将在2月17日至19日之间出现，这与实际数据非常接近。元胞自动机模型能模拟不同环境下疫情的发展变化，适合进行微观研究，同时也可以直观地比较政府采取强有力防控措施和消极防控的不同效果。