液压重载机械臂的精确建模与模态参数识别

高海勇，熊 健，张玉凯，张丰松

1洛阳矿山机械工程设计研究院有限责任公司 河南洛阳 471039

2国家矿山机械质量监督检验中心 河南洛阳 471039

3矿山重型装备国家重点实验室 河南洛阳 471039

近 年来，随着我国工业装备向着综合化、大型化、智能化的方向发展，重型工件的搬运、装配以及重型装备的维护作业等工业生产活动使得重型机械臂逐渐成为重载环境下不可或缺的核心技术装备。重载机械臂能够提高工作效率，降低风险，在未来工业发展中将逐渐取代大部分人力劳动[1]，为航空、矿山、冶金等工业领域提供安全保障。液压重载机械臂具有结构复杂，自重下挠及附属部件较多，需要进行空间上的自由移动、转动和大跨度轨迹作业，实现高精度、多自由度运动，同时工作环境比较恶劣，需要承受大载荷、高强度的工作压力，因此获取和掌握液压重载机械臂的动力学特性及模态参数是进行技术优化及改进的必然要求。

模态是机械结构特定的属性，包含固有频率、阻尼比和模态振型。通过计算分析法和试验模态法可以获取液压重载机械臂的动力学特性及模态参数。计算分析法通过有限元软件实现，但由于模型简化处理以及模型参数设置无法与实际设备完全一致而产生计算误差。模态试验法通过试验采集系统，对液压重载机械臂实施激励，获取的参数准确、全面、精度高[2]，可为机械臂有限元模型的计算优化提供可靠的试验数据。

1 试验模态分析

试验模态分析是通过激励装置对结构进行激励，同时测取激励和结构响应信号，经动态信号分析和模态参数识别，最终建立结构在已知激励条件下的响应模型，进而预测结构在各种振源作用下的实际振动响应。

机械结构动态特性用频响函数来描述，频响函数是测量得到的结构输出和输入的傅里叶变换之比[3]，频响函数

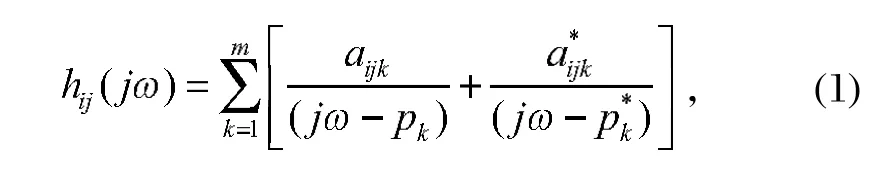
式中：aijk为留数，与模态振型直接相关；j为虚数，j=为系统的频率，Hz；pk为极点，包含了系统的频率和阻尼信息[4]，通过曲线拟合和识别算法，识别结构的模态参数。

2 精确几何建模

常规试验模态分析是利用图纸设计尺寸离散确定模态测点及几何模型，缺点是没有考虑安装及制造误差、重型设备因自重产生的空间变形等因素，造成测点位置不准确、几何模型有偏差。针对液压重载机械臂结构复杂、臂体下挠变形及附属部件较多等特点，利用激光跟踪仪测量基于计算模态分析结果选择的目标测点，直接、快速、准确得到机械臂模态测点的空间坐标，获取模态分析所需要的全部几何参数，实现试验模态分析的精确建模，提高模态参数识别的可信度。

激光跟踪仪测试系统如图 1 所示。在目标测点放置反射靶球，激光跟踪仪主机发射红色氦氖激光束至反射靶球，靶球将激光反射回跟踪仪主机，利用安装在跟踪仪主机俯仰角和方位角轴的角度编码器、干涉计，获取目标测点的水平方位角、俯仰角和距离r，根据激光跟踪仪坐标系得到目标测点的空间坐标。通过移动靶球，可以快速得到所有目标测点的空间坐标和构建模型。

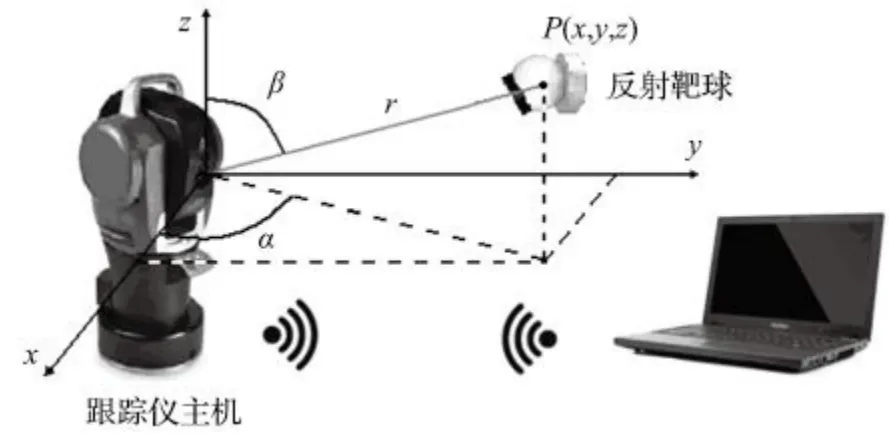
图1 激光跟踪仪测试系统Tab.1 Testing system with laser tracker

激光跟踪仪坐标系的目标测点坐标[5]为

3 机械臂模态试验

3.1 试验测点选取

机械臂试验模态测点布置遵循的原则：一是测点位置能有效显示各阶模态振型的变形特征及各阶模态振型的区别；二是选取的测点应避开机械臂的节点位置。基于以上原则，根据计算模态分析结果，测点位置示意如图 2 所示。

图2 测点位置示意Tab.2 Sketch of location of testing points

3.2 激光跟踪仪精确几何建模

利用激光跟踪仪进行空间扫描，可以快速得到机械臂模态测点的空间坐标，建立精确地模态试验几何模型。由于回转驱动、变幅液压缸、操作台等附属组件的遮挡，测取机械臂全部测点的空间坐标比较困难，经过多次尝试确定了激光跟踪仪主机的放置位置，该位置可以一次扫描到大多数测点。对于无法直接扫描到的测点，通过实测该点与可测点的相对空间距离，建模时给予修正补充。通过测量，以机械臂转台平面中心为坐标原点建立坐标系，得到机械臂转台、支座和臂体等部件的模态测点空间坐标，并导入试验模态分析软件，生成精确测点及几何模型。模态测点及模型如图 3 所示。

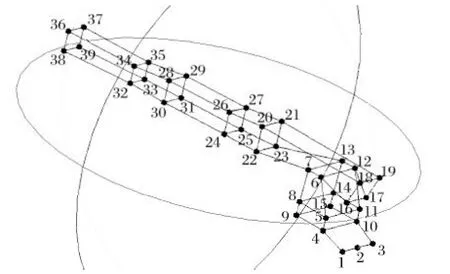
图3 模态测点及模型Tab.3 Modal testing points and model

3.3 边界条件和激励方式

重载机械臂样机安装于输送台车上。为了尽可能接近实际工作状态下的边界条件，确保获得真实可靠的动力学响应，试验时将输送台车牢固固定在刚性平台上，试验过程中保持支撑刚度不变，以保证试验模态结果的重复性和准确性。

由试验模态分析基本原理可知，获得频响函数的一行或一列就可以识别出模态矢量和极点位置，进而得到所有模态参数。考虑到仪器通道数量及机械臂的结构特点，试验选择激励点不动，依次移动响应测量点，每次测量 4 点响应。由 PCB 公司力锤加装软锤头分别在水平和垂直方向进行激励点输入，响应点输出通过 LMS 公司 SCADAS III 系统进行采集。为保证模态结果的准确性，各力、振动传感器使用校准器进行校准。

3.4 频响函数

试验模态测试中实时监控锤击效果、相干函数及频响函数。根据计算模态分析结果频率范围限定在0～100 Hz，相干系数 0.8 以上的数据被接受，最终筛选 10 次结果，通过 H1 估计法得到频响函数的最小二乘近似值。机械臂垂直方向的频响函数如图 4 所示。

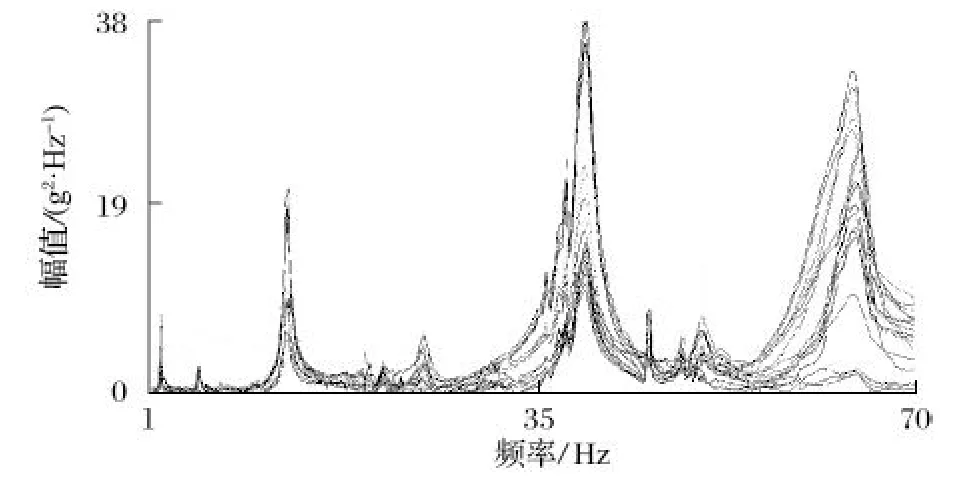
图4 机械臂垂直方向的频响函数Tab.4 Frequency response function of mechanical arm in vertical direction

由图 4 可知，除机械臂转台的个别测点外，臂体伸缩部分各测点的频响函数曲线光滑，一致性较好，峰值明显。

3.5 模态参数识别

模态参数识别使用 LMS 试验模态分析软件进行。估计极点数目和位置时，各测点测取的频响函数按幅值求和，使峰值显示在一个综合频响函数中。极点确定时，在稳态图的最低阶次中选择标有“s”(stable) 的真实模态频率，并与下一阶次极点的阻尼比进行比较，1 阶和 2 阶模态指示函数位于谷值时，可以认定该频率为真实稳定的模态频率。机械臂全伸长状态下垂直方向模态参数稳态图如图 5 所示。

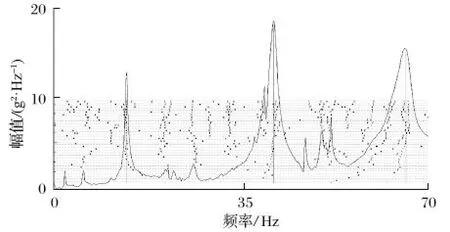
图5 机械臂垂直方向模态参数稳态图Tab.5 Steady-state diagram of modal parameters of manipulator arm in vertical direction

从图 5 可以看到 3 个明显的峰值，对应垂直方向的 3 个模态频率。根据模态频率识别原则，得到机械臂全伸长状态下的水平和垂直方向共 6 组模态参数，如表 1 所列。

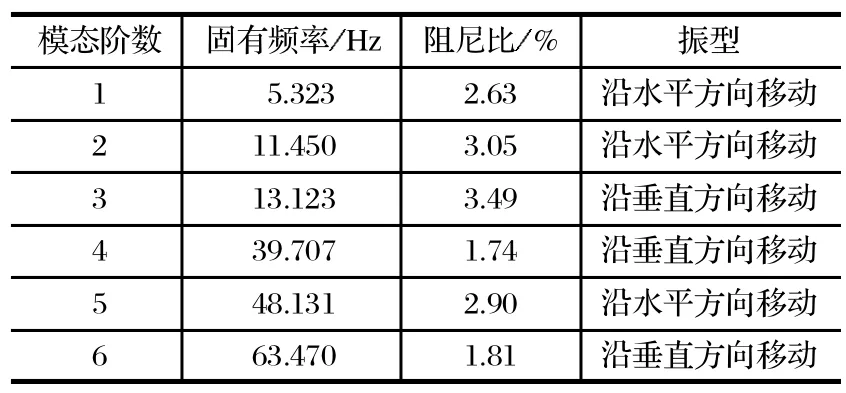
表1 机械臂前 6 阶试验模态参数Tab.1 Test modal parameters of preceding six orders of mechanical arm

由表 1 可知，机械臂系统的阻尼在 2%～4% 之间，属于大阻尼系统。机械臂前 6 阶试验模态振型如图 6 所示。

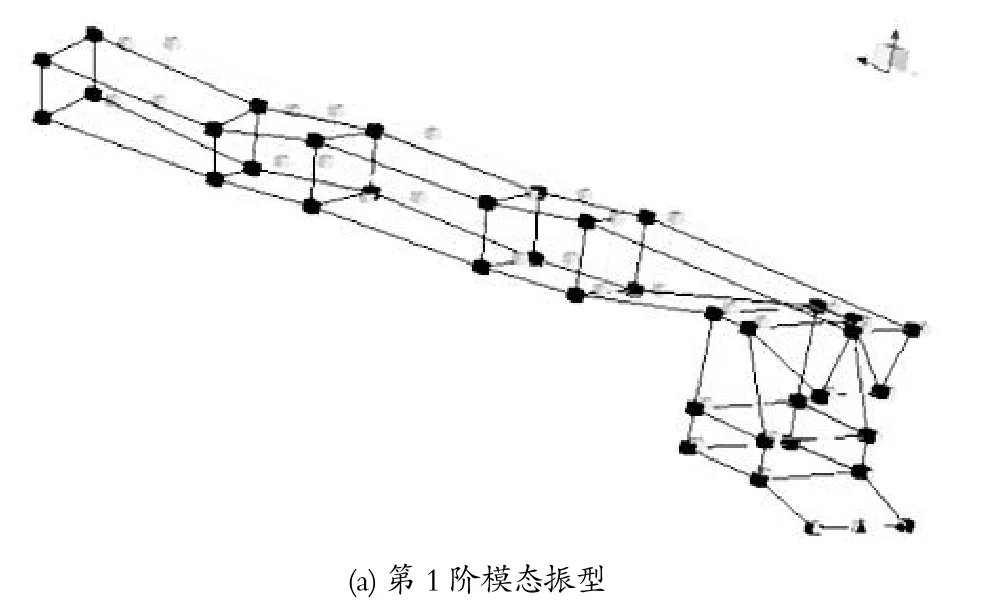
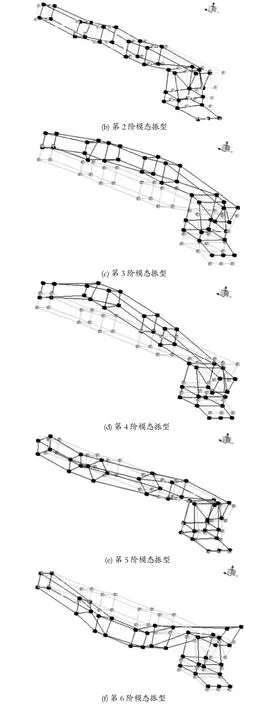
图6 机械臂前 6 阶试验模态振型Fig.6 Test modal vibration mode of preceding six orders of mechanical arm

3.6 结果验证

3.6.1 模态置信判据

模态置信判据 MAC 表示模态的可信程度[6]，用于比较模态阵型的一致性。它将 2 个模态的相关程度用 [0，1]的数值表示。如果 2 个模态阵型存在线性关系，则 MAC 值趋近于 1；反之，MAC 值将会趋近于0。机械臂水平和垂直方向的 MAC 判据矩阵如图 7 所示。

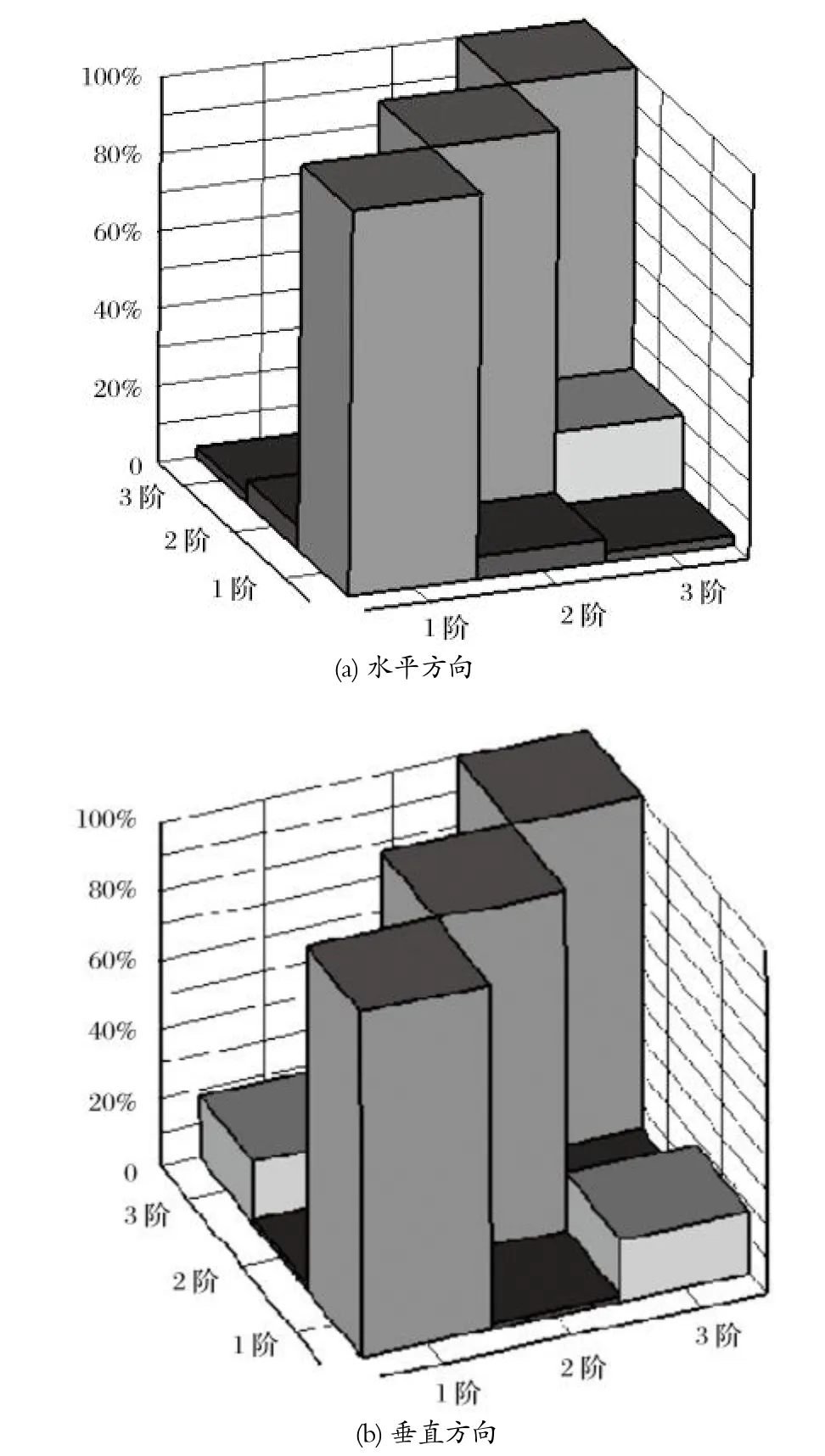
图7 机械臂的 MAC 判据矩阵Fig.7 MAC criterion matrix of mechanical arm

由图 7 可知，水平和垂直方向不同阶次之间最大的 MAC 值为 14.6%，表明各阶振型正交性较好，分析结果可靠。

3.6.2 模态复杂性验证

MPC 值越高，表明模态越接近真实模态，一般MPC 值应大于 90%。MPD 值越小，表明模态振型在相位上的分散程度越小，一般 MPD 值应小于 15%。机械臂水平和垂直方向的复杂性验证数值如表 2 所列。

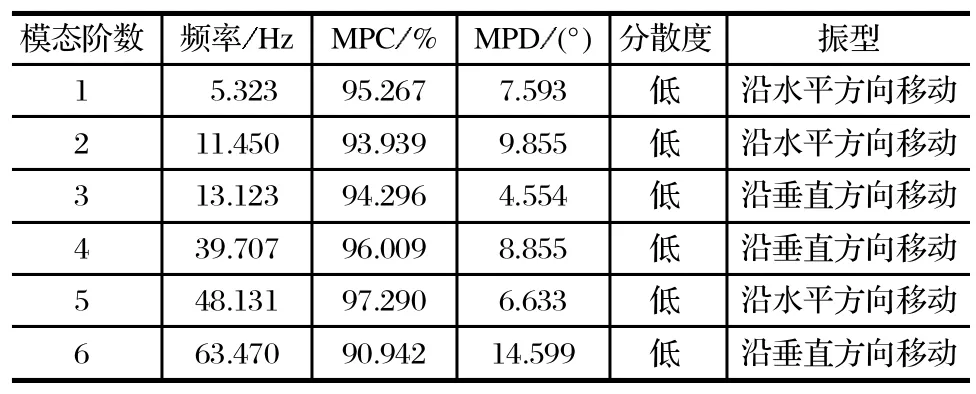
表2 各模态振型相关函数值Tab.2 Correlation function value of various modal vibration modes

4 计算模态和模态试验对比

机械臂计算模型采用设计参数进行仿真，简化了部分倒角、圆角和螺栓孔，忽略了液压系统阀体和供油管路。为了反映机械臂的实际工作状态，边界条件设置为后端固定约束，前 6 阶模态与模态试验对比如表 3 所列。

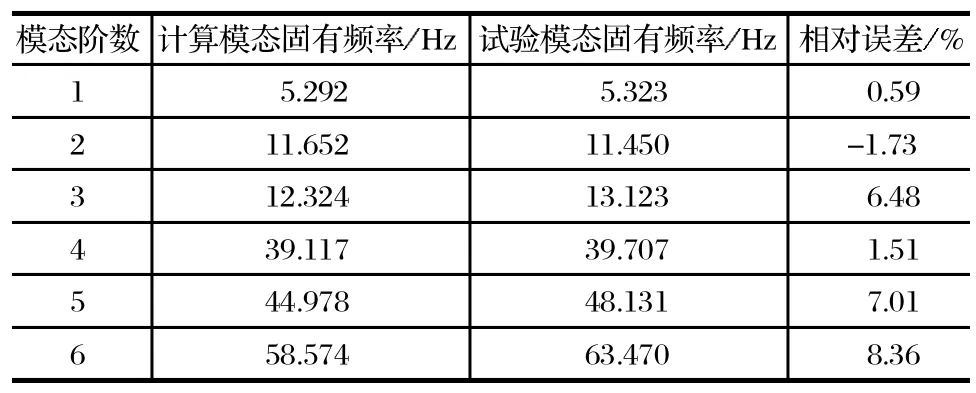
表3 计算模态和模态试验识别对比Tab.3 Comparison of calculated modes and test identif ied ones

由表 3 可知，试验模态识别出的前 6 阶固有频率值与有限元计算分析结果相对误差均在 10% 以内，通过模态数据对比得到计算模态和模态试验相似度较高，各阶模态振型均可靠。

5 结语

以液压重载机械臂为研究对象，通过试验模态法对机械臂进行模态参数识别，提取了可信的模态参数，并与计算模态进行了对比，误差在 10% 以内，验证了机械臂计算模态的可靠性。在试验过程中使用激光跟踪仪精确测量模态测点空间坐标，确保模态几何模型建立的准确性，提高了试验模态参数识别的可靠性，为机械臂的振动特性分析、结构动力特性的优化设计及故障诊断提供了可靠支持。