矿用挖装机履带行走机构动力学仿真
三一重型装备有限公司研究院 辽宁沈阳 110027
矿 用挖掘式装载机 (以下简称“挖装机”) 是用于煤矿井下平巷、斜巷的装载设备。该机的作业特点是行走时不挖掘,挖掘时不行走,行走机构既承受运输机构的间歇性载荷作用,又受工作机构不均匀载荷的影响,加之工作环境恶劣、工况复杂,导致行走机构常出现机械故障,降低工作效率和使用寿命。因此,研究不同工况下矿用挖装机行走机构的动力学性能具有重要意义。
为此,笔者通过分析整机,建立关键工况下的数学模型进行分析,从而得出其运动速度和履带板受力的变化规律,为进一步履带优化设计奠定基础。
1 工作力学模型的建立
1.1 矿用挖装机工作状态分析
矿用挖装机的工作状态有满载、坡道、倾斜、偏载、高位、低位、侧位等,笔者就最不利工况[1]32(满载坡道上行驶和作业) 研究其工作状态,如图 1 所示。该工况下挖装机的受力可通过力平移转化到行走机构上,得到行走机构的力和力矩。

图1 矿用挖装机工作状态Fig.1 Working status of mine-used backhoe loader
这时,履带行走机构主要受到地面支持力、车身压力、行走阻力、工作负荷的作用,履带工作于复杂的作业环境中。为简化分析,按照动力学建模理论和方法,采用离散体动力学模型法 (即将分布性质相似的质量浓缩成集中质量的离散化方法[2-3]) 将多节链环集中为质量块,建立纵向运行的动力学模型。
1.2 挖装机阻力模型
挖装机挖煤工作力为FA,其反作用力为FC(即煤对工作机构的作用力),FC经平移转化到行走机构上,得到挖煤阻力FW和力矩MW,如图 1 所示。挖煤阻力FW的大小与散煤矿力学分布特性密切相关,可以通过研究煤矿分布力得到挖煤阻力的随机过程。根据最大熵原理拟合的散煤矿力学特性与正态分布有很好的重合性[4],那么研究散煤的力学分布特性可以用正态分布简化。因此挖装机挖煤阻力模型用正态分布规律建立为
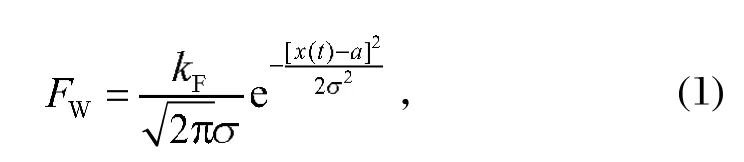
式中:kF为挖煤阻力幅值系数;x(t) 为任意时刻的挖煤阻力分布样本;a为正态分布的值;为正态分布的方差。
2 建立纵向运行动力学模型
履带行走机构是一个复杂的结构部件,其动力学模型是一个多自由度的系统。为方便计算与分析,根据实际结构和工作状态进行以下合理的假设与简化:①各部件质量均匀,最终简化为集中质量点;② 各连接部件之间的弹性很小,视各部件为无质量的元件连接,阻尼为黏性阻尼;③忽略驱动轮圆周线速度与履带链传动之间存在的多边形效应,假设传动速度连续平稳。

图2 矿用挖装机履带行走机构的纵向运行工况分析Fig.2 Analysis on crawler walking mechanism of mine-used backhoe loader in longitudinal motion mode
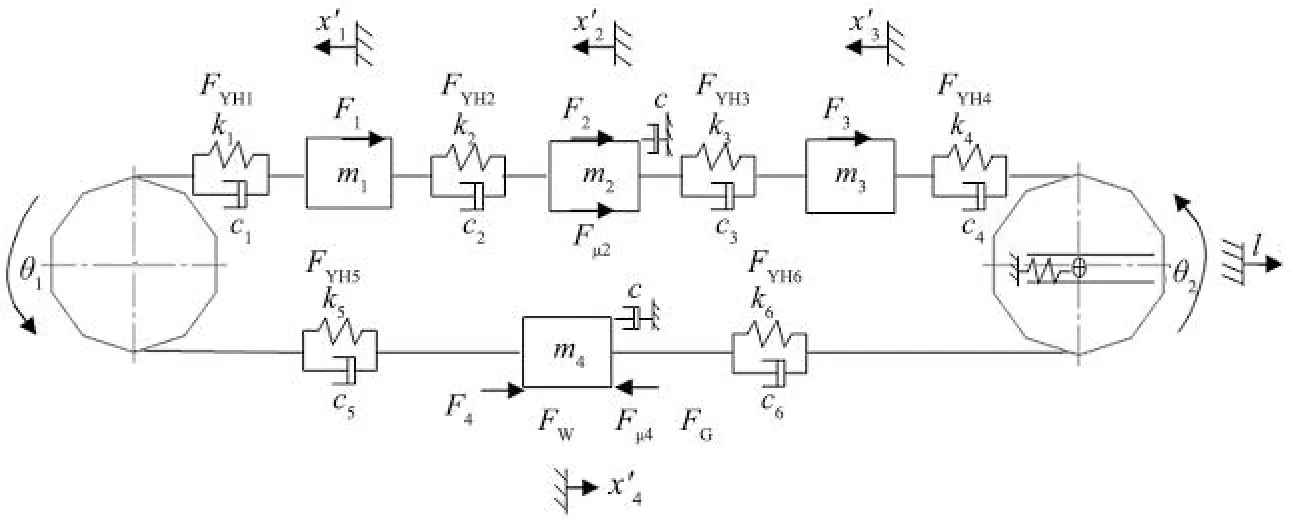
图3 矿用挖装机履带行走机构纵向运行的动力学模型Fig.3 Dynamic model of crawler walking mechanism of mine-used backhoe loader in longitudinal motion mode
取某型挖装机为研究对象,设驱动轮正向运行(逆时针运动),如图 2 所示。图 2(a) 折算成图 2(b)时,每个瞬时各段链的质量恒定。履带行走机构纵向运行的动力学模型如图 3 所示。上履带链相同性质的集中质量分别为m1、m2和m3,集中质量之间的刚度系数、阻尼系数分别为k2、c2和k3、c3,集中质量m1、m3与两端轮上履带链之间的刚度系数、阻尼系数分别为k1、c1和k4、c4。下履带链的性质一致,其集中质量为m4,m4与驱动轮、导向轮上履带链之间的刚度系数、阻尼系数分别为k5、c5和k6、c6,托链架和支撑轮阻力的等效阻尼为c。由于履带链是黏弹性体,取阻尼系数c1、c2、c3、c4、c5、c6相等。
任意时刻履带链拉力如下:

式中:FYH1、FYH2、FYH3、FYH4、FYH5、FYH6分别为导向轮与m1轮、m1与m2、m2与m3、m3与驱动轮,导向轮与m4、m4与驱动轮之间的链拉力;F1、F2、F3、F4分别为集中质量m1、m2、m3、m4所受的下滑阻力;x1、x2、x3、x4分别为集中质量m1、m2、m3、m4的位移;Fμ2、Fμ4分别为集中质量m2、m4的摩擦阻力;FV为预紧力;FG为挖装机坡道阻力;q为履带链的密度;g为重力加速度;R1、R2分别为导向轮、驱动轮的半径;分别为导向轮、驱动轮的转角。
3 仿真分析
3.1 坡道行走不作业工况分析
某型矿用挖装机最大爬坡角为 30°,必须预紧力FV=35.28 kN[8],并正向运行 0~10 s,集中质量m1、m2、m3、m4两端的链拉力变化依次如图 4(a)~(f) 所示,驱动转矩如图 4(g) 所示,矿用挖装机的行驶速度(即履带链集中质量m4的速度) 如图 4(h) 所示。
统计集中质量m1、m2、m3、m4两端链拉力的仿真结果,如表 1 所列,稳定速度均值为低于矿用挖装机行驶速度基准可见此仿真符合实际运行工况。


图4 行走不作业运行仿真结果Fig.4 Simulation results in walking and non-operating mode

表1 行走不作业时履带链拉力的仿真结果Tab.1 Simulation results of traction of crawler chain in walking and non-operating mode kN
矿用挖装机行走不作业工况下的仿真结果表明:刚起步时,履带链拉力变化幅值最大,随着运行速度的增加,拉力幅值逐渐减小,然后趋于稳定。随着运行的持续,拉力均值趋于稳定,拉力幅值增加到稳定值。从统计分析看,靠近驱动轮端的履带链是紧边,上侧紧边链拉力均值和标准差比下侧紧边链拉力均值和标准差大,在托链架上的履带链处于最危险工况。
3.2 坡道作业不行走工况分析
在最大作业坡度上,提供一个制动力矩 (见图5(h)),使矿用挖装机不行走 (即集中质量m4不动),取预紧力FV=35.28 kN[5],挖煤阻力如图 5(g) 所示,并正向运行 0~10 s,得到矿用挖装机在该工况下集中质量m1、m2、m3、m4两端的链拉力变化情况,依次如图 5(a)~(f) 所示。

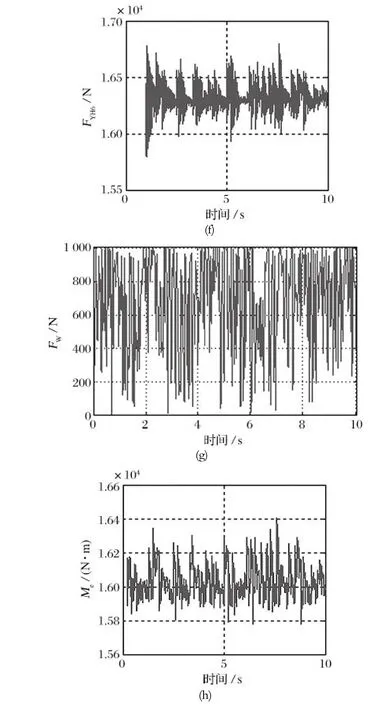
图5 作业不行走运行仿真结果Fig.5 Simulation results in operating and non-walking mode
统计集中质量m1、m2、m3、m4两端链拉力的仿真结果,如表 2 所列。

表2 作业不行走时履带链拉力的仿真结果Tab.2 Simulation results of traction of crawler chain in operating and non-walking mode kN
矿用挖装机作业不行走工况下的仿真结果表明:履带链拉力处于动态平衡中,并随着挖煤阻力的干扰有所增加,然后趋于平稳。从统计分析看,靠近驱动轮端的履带链是紧边,上侧紧边链拉力均值和标准差比下侧紧边链拉力均值和标准差大,即靠近驱动轮的上侧履带链处于最危险工况。
4 结论
(1) 行走仿真结果表明:刚起步时履带链拉力变化幅值最大,随着速度的增加,拉力幅值逐渐减小,然后趋于稳定,且近驱动轮端的履带链是紧边,上侧链拉力比下侧链拉力大,在托链架上的履带链处于最危险工况。
(2) 作业仿真结果表明:作业时履带链拉力处于动态平衡中,并随着挖煤阻力的干扰有所增加,然后趋于平稳,且靠近驱动轮端的履带链是紧边,靠近驱动轮的上侧履带链处于最危险工况。
不同工况下履带行走的仿真研究为履带行走机构的合理设计和正确使用提供了理论依据。

