自适应动态学习鸡群优化算法

顾艳春，鲁海燕 ，2，向 蕾，沈莞蔷，2

1.江南大学 理学院，江苏 无锡 214122

2.江南大学 无锡市生物计算工程技术研究中心，江苏 无锡 214122

1 引言

群智能优化算法是通过模拟自然现象的物理规律及自然界各类生物种群的生活习性和行为特点而构造的一类随机优化算法，如遗传算法[1-2]（Genetic Algorithm，GA）、粒子群算法[3-4]（Particle Swarm Optimization，PSO）、蝙蝠算法[5]（Bat Algorithm，BA）、蜂群算法[6-7]（Artificial Bee Colony，ABC）等。这些算法为解决大量存在于计算科学、工程科学、管理科学等领域的复杂问题提供了新的求解途径。

鸡群算法[8]（Chicken Swarm Optimization，CSO）是2014年由孟献兵等人提出的一种智能优化算法，该算法具有原理简单、易于实现和全局搜索能力较强等优点，因此被广泛研究并应用于图像处理[9]、电网优化[10]、传感器与通信[11]等优化问题[12-14]。但鸡群算法也存在求解精度偏低、局部求解能力较弱等问题，因此，众多学者进行研究改进，提出了一系列改进鸡群优化算法。李振壁等人[15]将模拟退火的思想引入鸡群算法，提高了算法的寻优性能。史旭栋等人[16]把鸡群算法和人工蜂群算法相融合，平衡了算法的全局和局部搜索能力。张慕雪等人[17]在算法的公鸡更新公式中添加了向当前最优个体和最差个体学习部分，提高了算法跳出局部极值的能力。郑家明等人[18]在算法中用佳点集构造初始种群，并引入了寻食速度因子和聚集度因子，提高了算法的稳定性和求解精度。张莹杰等人[19]改进了鸡群算法的边界约束处理机制，提高了算法的收敛速度。韩萌[20]将耗散结构引至公鸡位置的更新中，并对随机选择的个体进行差分变异操作，增强了算法的全局搜索能力。

上述改进算法在一定程度上提高了算法的寻优能力，但仍存在着一些不足。比如，有些改进算法虽然提高了算法的求解精度，但算法的收敛速度较慢；还有些改进算法在求解高维问题上，仍存在早熟收敛等问题。为此，本文提出自适应动态学习鸡群优化算法（ADLCSO），利用反向觅食机制和非线性递减的学习因子来动态地自适应更新种群中的公鸡位置，以提高公鸡个体跳出局部极值的能力，从而提高求解精度和收敛速度；同时利用整个种群中个体间适应度值之差定义了一种新的种群相似度指标，根据该指标使母鸡个体进行自适应更新，在保持种群多样性的同时使母鸡个体朝着对整个群体较为有利的方向觅食。通过对12个经典测试函数的仿真实验，结果表明上述两个更新策略能够有效地提高鸡群算法的求解精度和收敛速度，特别是在求解高维问题上ADLCSO算法比标准鸡群算法有显著优势。

2 鸡群优化算法

鸡群算法是模拟鸡群的等级制度和觅食行为的一种随机优化算法，该算法遵循如下规则：

（1）将整个鸡群分成若干子群，每个子群都由一只公鸡，若干只母鸡和小鸡组成，即子群的个数由公鸡的个数决定。

（2）按照每只鸡适应度值的大小将种群分为公鸡、母鸡和小鸡三种，其中适应度较好的若干个体为公鸡，适应度较差的若干个体为小鸡，其余的为母鸡。

（3）公鸡、母鸡、小鸡三者之间的等级制度一旦确立将数代保持不变，等级制度每隔G(G∈[2,20])代更新一次。

（4）每个组内母鸡跟随该组的公鸡觅食，也可随机偷取其他组内食物；每组内小鸡跟随妈妈母鸡进行觅食。

（5）每一只鸡的位置都对应优化问题的一个解。假设在一个种群里有N个个体，公鸡、母鸡、小鸡、妈妈母鸡的数量分别为NR、NH、NC、NM。妈妈母鸡是从母鸡中随机选取，每个母鸡妈妈有若干个孩子小鸡。

（6）在鸡群中，不同等级的鸡的位置更新方式有所不同。公鸡作为适应度最好的鸡群，在整个觅食过程中占据主导地位，可以在更广泛的空间里寻找食物。公鸡位置更新公式如下：

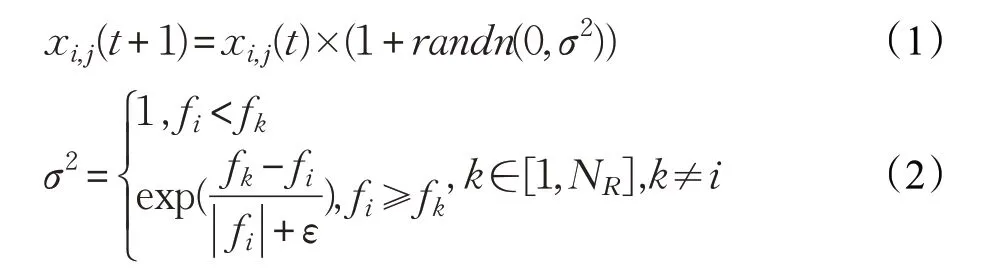
其中，randn(0,σ2)是均值为0、标准差为σ2的一个高斯分布；fi为个体i的适应度值；ε为充分小的正数，以防止的分母取值为0；k为任一公鸡个体的编号，且k≠i。

母鸡位置更新公式如下：

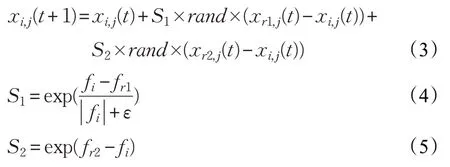
其中，r1 为第i只母鸡的配偶公鸡个体的编号，r2 为随机选取的任一公鸡或母鸡个体的编号，且r1 ≠r2，rand为[0，1]内的随机数。

小鸡位置更新公式如下：

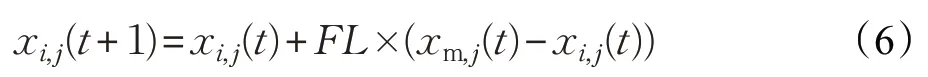
其中，xm,j(t)代表第t次迭代时第i只小鸡的妈妈的位置，FL(FL∈[0,2])为跟随系数。

3 自适应动态学习鸡群算法

本文在标准鸡群优化算法中引入了非线性递减学习因子和反向觅食机制，使公鸡个体在向全局最优个体动态学习的同时还自适应地进行反向觅食，可提高算法跳出局部极值的能力；此外定义了种群相似度指标，根据该指标使母鸡个体进行自适应更新，可进一步提高算法的性能。

其中，tmax为总迭代次数；w(t)为第t次迭代的学习因子；wmax和wmin为学习因子的最大值和最小值(wmax=0.9,wmin=0.4)。

在算法迭代前期，学习因子较大，从而使公鸡个体有较大的学习范围，不仅能扩大搜索区域，还能有利于跳出局部极值；而在算法后期搜索阶段学习因子较小，有利于提高公鸡群体的局部搜索能力，从而有利于找到全局最优值。

3.1.2 公鸡个体向最优个体学习

公鸡群体是整个种群中适应度值最好的群体，它起着引领其他群体向全局最优位置前进的作用。为了加快整个种群搜索到最优解的速度，本文使公鸡个体在向自身学习的同时还要向当前种群中最优个体动态学习，从而能够使公鸡个体尽快地进入最优解附近的区域。改进的公鸡更新公式如下：

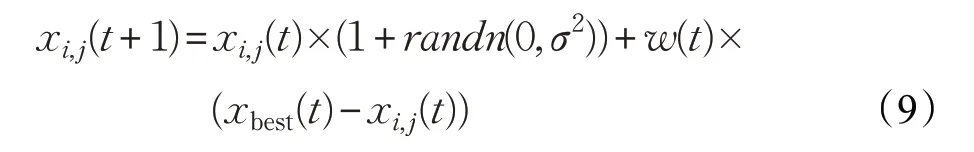
其中，xbest(t)为第t次迭代最优个体的位置。

3.1.3 反向觅食机制

公鸡个体向当前种群中最优个体学习虽然能够提升算法的收敛速度和求解精度，但在解决高维多峰函数时容易使大多数个体聚集在局部极值附近难以跳出，算法会出现早熟收敛的情况。

为了合理地判断算法是否陷入局部极值，本文通过计算从第t+1-K次迭代到第t次迭代出现的K个最优解的方差来检测算法是否早熟收敛，计算公式如下：

3.1 基于反向觅食机制的公鸡位置更新

3.1.1 非线性递减学习因子

为了能较好地平衡鸡群算法的全局和局部的搜索能力，本文在鸡群算法的公鸡更新公式中引入非线性递减的学习因子，该学习因子的公式如下：

其中，δ(t)为第t+1-K次迭代到第t次迭代出现的K个最优解的方差；xmean为K个最优解的均值。当δ(t)＜ε（ε为充分小的正数），表明连续K次迭代最优解没有发生明显变化，则可认为算法出现早熟收敛现象。

为了提高算法跳出局部极值的能力，文献[17]在算法陷入局部极值时使公鸡个体向当前整个种群中最差粒子学习，使得整个鸡群能够以一定的概率跳出局部最优区域，文献[17]中的公鸡更新公式为：

其中，xworst(t)为第t次迭代的最差解向量；Q为学习系数，在文献[17]中Q=0.5。

文献[17]的改进策略一定程度地增强了算法跳出局部最优的能力，但使用常数学习系数不利于平衡全局与局部的搜索能力。为此，本文在公鸡位置更新中引入反向觅食机制，当算法陷入局部极值时使公鸡个体向远离全局最优位置的方向进行觅食，并且在更新公式中加入了非线性递减的学习因子。此时公鸡个体的更新公式为：

其中，xbest(t)为第t次迭代的最优个体的位置。

3.2 基于种群相似度指标的母鸡位置更新

3.2.1 种群相似度指标

当前种群的多样性与算法的搜索能力密切相关，当种群多样性较差时，算法的全局搜索能力较弱。因此，一些学者通过定义种群中个体之间的密集度来衡量当前种群多样性的高低。王丛佼等人[21]定义群体适应度值方差来反映种群中所有个体聚集程度，以此来改进差分进化算法。何琼月等人[22]在改进粒子群算法时，用当前粒子之间的欧氏距离来定义种群的相似度。

本文在鸡群算法中引入种群相似度概念，利用当前整个种群中每个个体与最优个体之间的适应度的差来定义整个种群的相似度，继而根据种群的相似度对母鸡个体进行自适应更新。当两个个体之间的适应度差值较大时，很容易判断这两个个体相似度较低；当两个个体之间的适应度差值较小时，对个体之间相似度的判断则较为困难。为了合理度量两个个体之间的相似度高低，本文在设计相似度指标函数时需要遵循以下几点要求：

（1）函数的值域为(0,1)。

（2）在自变量较小时，函数值对自变量变化比较敏感，函数的图像较陡。

（3）在自变量较大时，函数值受自变量变化的影响较小，函数的图像较缓。

遵循以上几点要求，定义个体之间的相似度指标公式如下：

其中，fi为个体i的适应度值；fp为当前种群中最优个体的适应度值；u(i,p)为个体i与最优个体的相似度指标；a为固定常数，大量实验表明，当a=5 时算法求解效果较好。

通过分析公式（14）知，函数u为增函数，当两个个体之间适应度的差值越大时，个体之间的相似度指标越大，两个个体之间相似度就越低。为了更加直观地看出相似度指标函数图像前陡后缓的特点，特地给出了函数图像（见图1）。

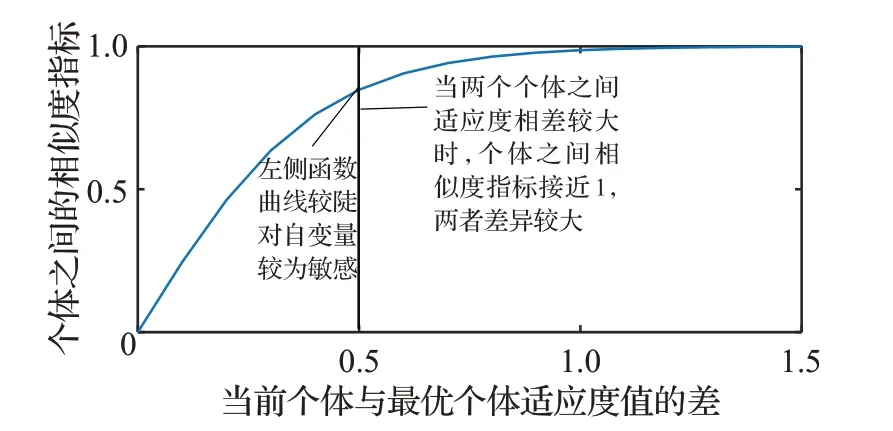
图1 u 函数的曲线图

由公式（14）可得到个体与最优个体之间的N（种群个数）个相似度指标值，然后对这N个指标值进一步求均值来度量整个种群的相似度。种群相似度指标s(t)的表达式如下：

其中，s(t)表示第t代的种群多样性指标。当s(t)→1时，种群中个体的相似度较低，种群多样性较好；当s(t)→0 时，种群中个体的相似度较高，种群多样性较差。

3.2.2 母鸡个体更新方式

根据上述的种群相似度指标，本文改进的母鸡更新公式如下：

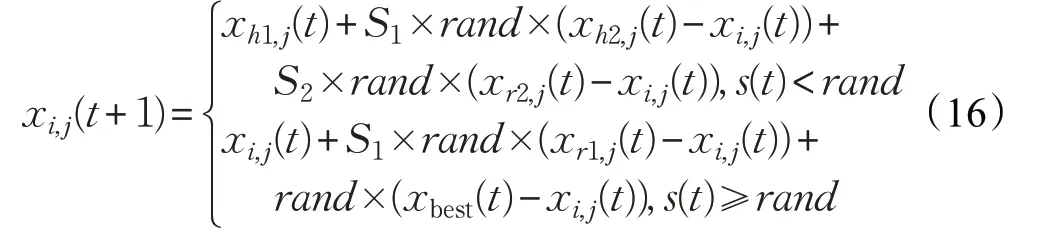
其中，h1 和h2 为鸡群中的随机个体的编号。若s(t)＜rand，则第i只母鸡选择随机粒子进行随机学习，以增加种群多样性；若s(t)≥rand，则第i只母鸡选择最优个体和自身所在子群的公鸡个体学习，从而促使个体向最优解靠近。

3.3 ADLCSO算法的求解步骤

自适应动态学习改进鸡群算法（ADLCSO）的求解步骤如下所述：

（1）种群初始化。设置种群数量N，公鸡个数NR，母鸡个数NH，小鸡个数NC，小鸡妈妈的个数NM，进化代数G，最大迭代次数tmax等相关参数。

（2）计算鸡群里每个个体的适应度值，设置整个鸡群全局最优位置，设置迭代次数t=1。

（3）根据公式（7）～（8）计算学习因子；根据公式（14）～（15）计算当前种群相似度指标值。

（4）若mod(t,G)=1，则根据鸡群里每个粒子的适应度值对鸡群里每个个体进行排序，建立等级制度。

（5）如果t≥K,则根据公式（10）～（11）计算方差δ(t),然后转步骤（6）；否则转步骤（7）。

（6）如果δ(t)＜ε，则转步骤（8）；否则转步骤（7）。

（7）根据公式（9）对公鸡个体进行更新。

（8）根据公式（13）对公鸡进行位置更新。

（9）然后根据公式（16）对母鸡位置更新。

（10）根据公式（6）对小鸡位置更新。

（11）更新鸡群中的全局最优位置，t=t+1。

（12）若满足算法终止条件，则迭代停止，输出最优解；否则转步骤（3）。

4 数值实验与结果分析

4.1 算法参数设置和测试函数

本文通过12 个基准测试函数对本文改进算法（ADLCSO）进行测试。为了保证比较的公平及合理性，令所有算法的种群规模为100，迭代次数为1 000，独立运行30 次，所共有参数保持一致。各算法的参数设置见表1。在12 个测试函数中，f1～f4为单峰函数，f5～f11为多峰函数，f12为固定维数的多峰函数。函数理论最优值都为0，12个基准测试函数表达式如下：

（1）Sphere函数

（2）BentCigar函数

（3）Discus函数

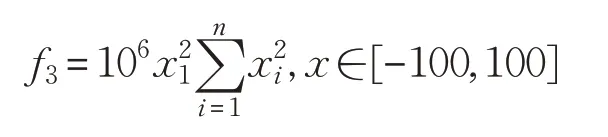
（4）High Conditioned Elliptic函数：

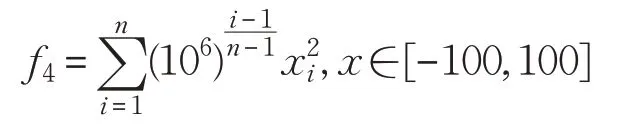
表1 三种算法的参数设置

（5）Ackley函数

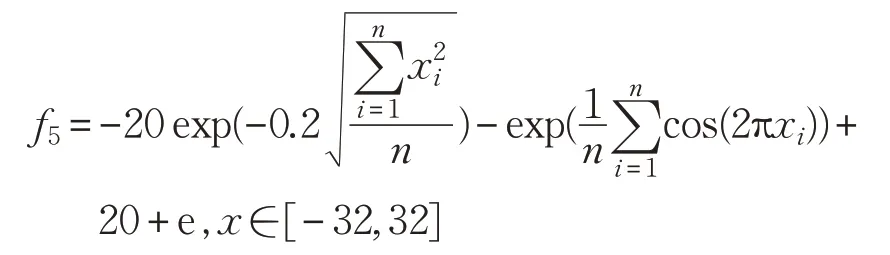
（6）Griewank函数

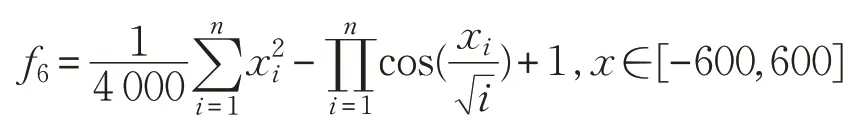
（7）Rastrigin函数

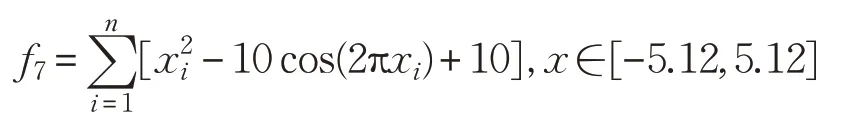
（8）Powell函数

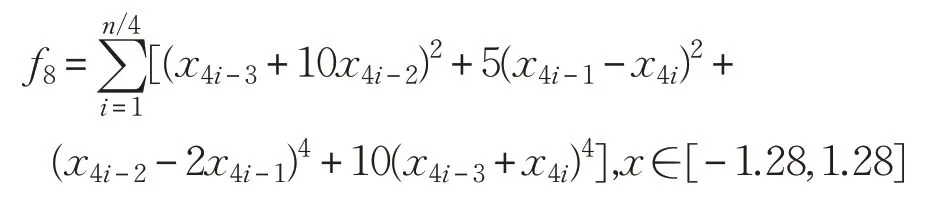
（9）Alpine函数

（10）Quartic函数

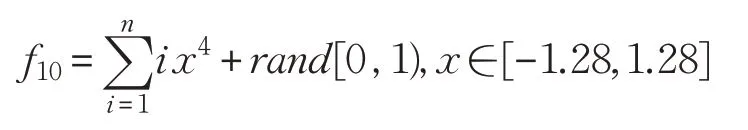
（11）Zakharov函数

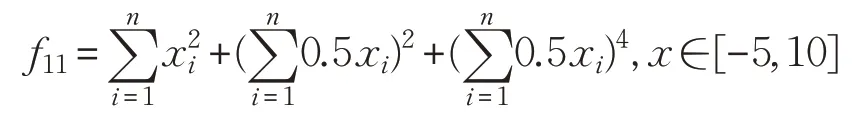
（12）Bukin函数

4.2 两种改进策略的有效性分析

为了验证反向觅食机制和种群相似度指标的可行性和有效性，本文利用上述12 个函数对ADLCSO-I 算法和ADLCSO-II 算法进行测试。这里ADLCSO-I 算法是在CSO算法中只引入基于反向觅食机制的公鸡位置更新策略；ADLCSO-II 算法是在CSO 算法中只引入基于种群相似度指标的母鸡位置更新策略。ADLCSO-I算法和ADLCSO-II算法中的参数设置同表1中ADLCSO算法的参数设置相同。表2为对比实验结果，图2为3种不同策略对单峰函数f1和多峰函数f7的收敛图。

图2 部分测试函数的收敛图

由表2 和图2 可以看出，使用两种改进策略的ADLCSO算法的寻优精度、收敛速度和寻优稳定性都要优于使用单一改进策略的ADLCSO-I算法和ADLCSO-II算法，ADLCSO-I 算法在大多函数优化上的表现优于ADLCSO-II 算法。单独使用反向觅食机制和种群相似度对标准鸡群算法性能的改进虽然有一定的效果但效果有限，组合的改进策略可以更加有效地提高算法的寻优性能。

4.3 学习因子的有效性分析

本文在公鸡个体位置的更新公式中加入了非线性递减的学习因子，为了验证该策略的优越性，利用上述前9个测试函数对ADLCSO-I和ADLCSO-Iw进行实验对比。这里ADLCSO-Iw算法是把ADLCSO-I算法中的学习因子替换成文献[17]中的常数因子(w=0.5)。表3为实验结果，图3表示两种算法寻优收敛曲线图。

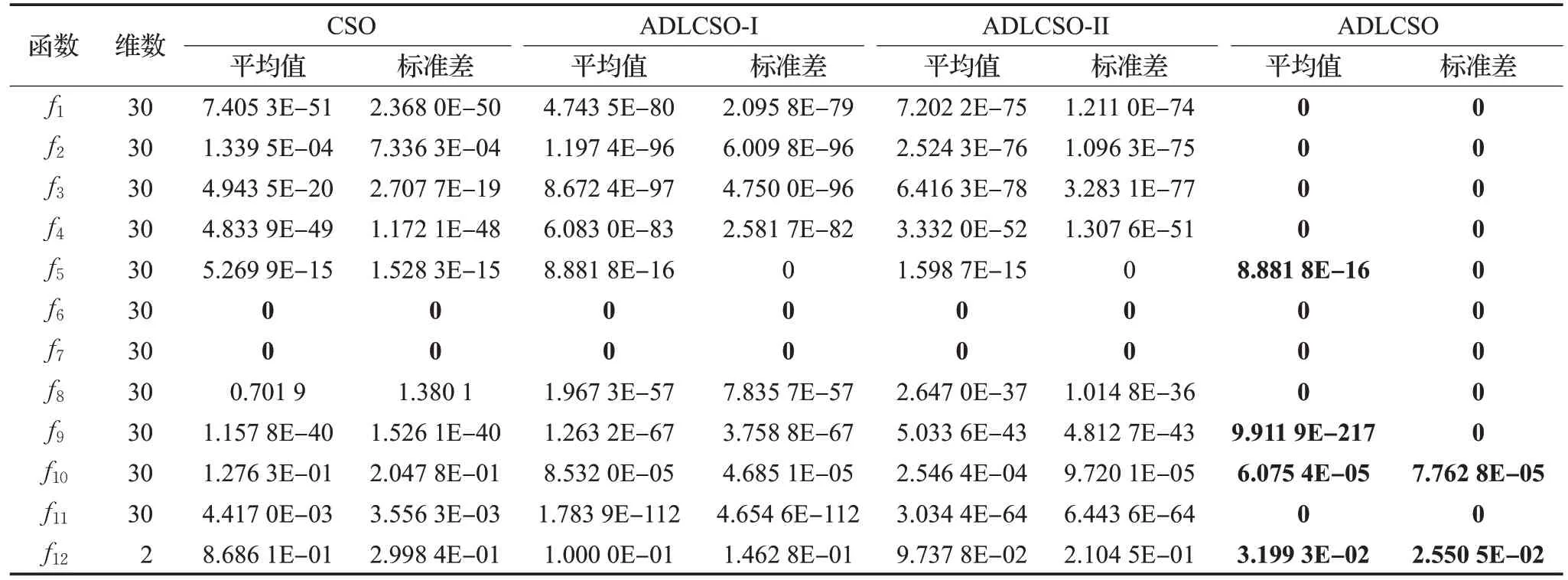
表2 不同改进策略下ADLCSO算法的测试结果

由表3中数据可以看出，对于函数f1～f4和f8～f9来说，ADLCSO-I 算法的求解精度要优于ADLCSO-Iw 算法。对于函数f5～f7，两种学习因子求得的结果相同，但从图3 上可以看出，ADLCSO-I 算法比 ADLCSO-Iw 算法的收敛速度有明显的提高。综上分析，无论是求解单峰函数还是多峰函数，非线性递减的学习因子总体上都要优于常数学习因子。

4.4 与标准算法实验对比

本文通过求解上述12 个测试函数对标准鸡群算法（CSO）、标准粒子群算法（PSO）和本文改进算法（ADLCSO）的性能进行比较。各算法参数设置见表1。表4 记录了3 种算法求解的结果，图4 表示在30 维问题上3种算法的收敛曲线图。

图3 ADLCSO-I算法和ADLCSO-Iw算法求解部分测试函数的收敛图

4.4.1 寻优精度分析

从表4中可以看出，对于大部分测试函数，ADLCSO算法得到的平均值和标准差都为0，这说明ADLCSO算法的求解精度和稳定性比其他两种算法更高。

对于多峰函数f5、f9和f10，CSO 算法和 PSO 算法的寻优精度明显不如ADLCSO 算法，并且随着维数的增加，CSO 算法和PSO 算法的寻优效果有所下降，但ADLCSO 算法在高维上依旧能收敛到较高精度。对于多峰函数f6和f7，在10 维和30 维问题上CSO 算法和ADLCSO 算法的求解结果都达到了0，PSO 算法求解结果较差；但是在100 维的问题上时，CSO 算法和PSO 算法都出现陷入局部极值，ADLCSO算法却依旧能收敛到最优解。对于函数f11，CSO算法和PSO算法陷入局部极值，但ADLCSO算法在求解100维问题时求解精度达到了2.175 8E-205。以上分析说明在求解高维问题时，CSO算法和PSO算法都容易陷入局部极值，但ADLCSO算法依旧能收敛到较高精度，甚至对于大部分函数能求解到理论最优值。

4.4.2 收敛速度分析

由图4 可以看出，随着迭代次数的增加，ADLCSO算法的收敛曲线下降很快，且在求解大部分函数时都能快速收敛到理论最优解。

为了对比ADLCSO 算法在求解不同维数上的性能，本文给出了ADLCSO 算法在不同维数下的收敛图（图5）。从图5 的收敛曲线可以得到，即使在求解高维问题时，ADLCSO算法的收敛速度仍然很快。

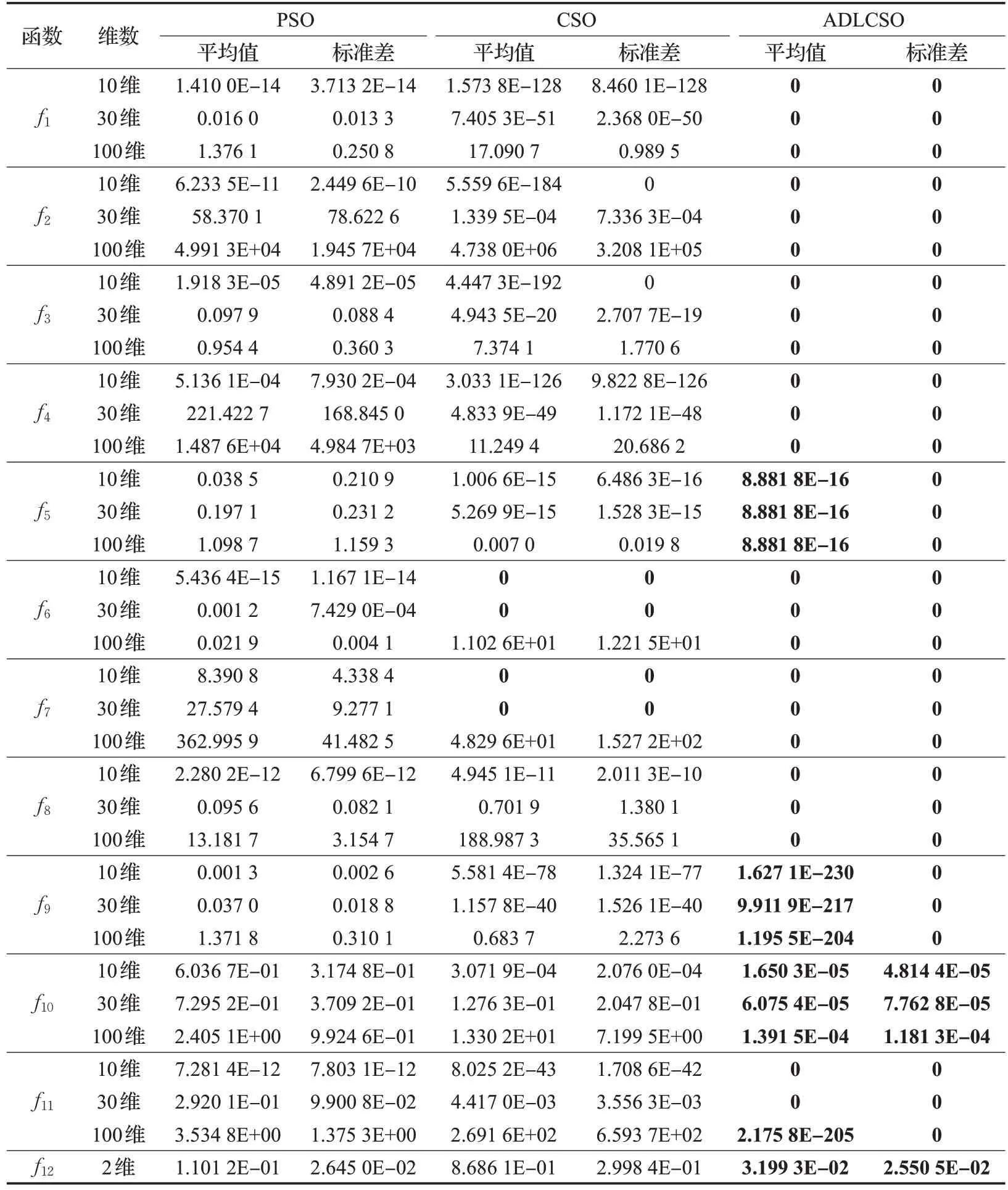
表4 三种算法的性能测试结果

综合以上分析，与CSO 算法和PSO 算法相比，ADLCSO算法在稳定性、求解精度与收敛速度上均有显著提高。

4.5 与其他改进鸡群算法的比较

将本文所提出的ADLCSO算法与PRCSO[17]、ICSO[18]、ICCSO[19]、DMCSO[20]和 GCSO[23]进行对比，对比数据见表5。5种改进鸡群算法的参数设置和数据均来自于对应的参考文献。在表5 中，D为算法求解的问题维数，T为算法最大迭代次数。

由表5可以看出，ADLCSO算法的求解结果整体上优于其他5种对比算法。

维数为30，算法迭代次数为500 时，ADLCSO 算法的寻优效果明显优于ICSO 算法。对于函数f6和f7，ADLCSO 算法和ICSO 算法的求解结果都为0，但是由图4的收敛曲线可知，在求解函数f6和f7时，ADLCSO算法在迭代40次左右就收敛了，而从文献[18]中可以看出ICSO算法在迭代300次左右才收敛。

维数为 100，迭代次数为1 000 时，ADLCSO 算法求解的结果整体上优于DMCSO 算法和GCSO 算法。对于函数f5，ADLCSO算法的求解的平均值稍差于GCSO算法；但是ADLCSO 算法得到的标准差却为0，在求解稳定性上ADLCSO算法明显优于GCSO算法。

以上分析说明，与以上5 种相关改进算法相比，ADLCSO算法的求解性能最好。

4.6 ADLCSO算法的时间复杂度分析

在标准鸡群算法CSO 中，假设解空间的维数为n，种群大小为N，各参数的初始设置、生成一个均匀随机数、求目标函数值、将所有个体的适应值排序并得到当代最优个体适应度值的时间分别为t1、t2、f(n)、t3，则算法初始化阶段的时间复杂度为：

图4 3种算法求解测试函数的收敛图

图5 ADLCSO算法在不同维数下的部分测试函数收敛图

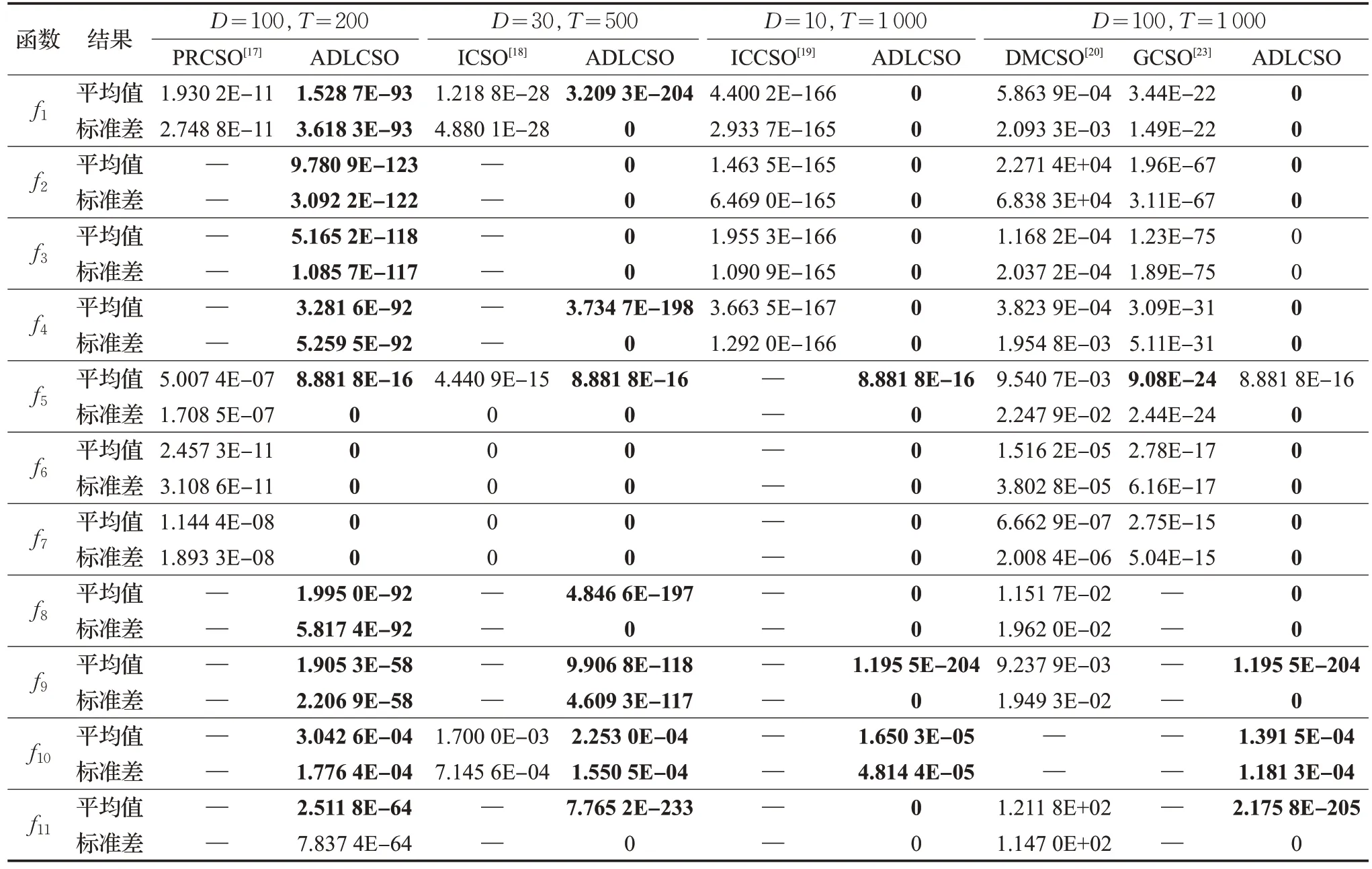
表5 不同改进算法的对比实验结果

进入迭代后，在鸡群个体位置更新阶段，假设：迭代次数为m，公鸡个数为N1，母鸡个数为N2，小鸡个数为N3，新产生个体的适应度计算时间为f(n)；公鸡个体每一维进行位置更新的时间为t4；母鸡个体每一维进行位置更新的时间为t5；个体每一维进行位置更新的时间为t6；新旧个体适应值比较互换的时间为t7；每一次更新种群等级制度的时间为t8；则鸡群个体位置更新阶段的时间复杂度函数为：

综上所述，标准鸡群算法的时间复杂度为：

ADLCSO 算法在标准鸡群算法的基础上增加了公鸡位置更新中的学习因子、方差和母鸡位置更新中的相似度指标。假设：计算一次迭代的学习因子的时间为t9，计算一次迭代的方差的时间为t10，计算当前个体与最优个体的相似度指标的时间为t11，则计算学习因子、方差和相似度指标的时间复杂度为：

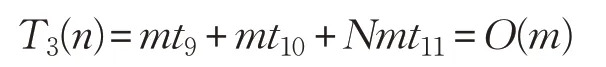
从而ADLCSO算法的时间复杂度为：

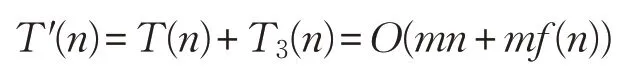
由此可知，本文算法ADLCSO 和标准鸡群算法CSO的时间复杂度依旧在同一个数量级。

5 总结

本文在鸡群算法的基础上提出了自适应动态学习鸡群优化算法，在算法中引入反向觅食机制和种群相似度指标，分别对公鸡和母鸡的位置更新公式进行自适应调整，并在公鸡位置更新公式中加入非线性递减学习因子。反向觅食机制增强了种群跳出局部极值的能力，提高了算法的收敛速度和求解精度；非线性递减学习因子的引入较好地平衡了算法全局探索和局部开发能力，增强了算法的稳定性；通过种群相似度指标对母鸡的位置进行自适应更新，抑制了种群多样性的衰减，提高了算法的求解精度。最后，通过对12 个经典测试函数的仿真实验，验证了ADLCSO算法的优越性。