无油涡旋压缩机涡旋齿温度场的数值计算

彭 斌，李 建，杜建平

（1.兰州理工大学机电工程学院，甘肃兰州 730050；2.浙江蓝德华燕动力有限公司，浙江绍兴312300）

1 引言

无油涡旋压缩机是第三代容积式压缩机，具有可靠性高、结构简单、噪声小、振动低、效率高的特点。其利用动、静涡旋齿之间的相互啮合而成的月牙形腔进行压缩气体，此工作过程中，将吸入的气体逐渐压缩至排气孔排出，气体随着腔体的压缩逐渐升高，并与涡旋齿壁面进行对流换热，涡旋齿壁面的温度载荷对工质在腔内增压会产生较大的泄漏，因此在涡旋压缩机的工作过程中涡旋齿的温度场实际分布情况至关重要。

国内外学者对涡旋压缩机工作过程中涡旋齿温度分布情况的探究中，李风宁等运[1-3]用有限元软件分析了涡旋齿的温度场分布；羊玢等[4-6]利用不同的形式对涡旋齿的温度场分布进行了计算；王君等[7-8]利用力学模型对无油涡旋压缩机的研发和性能分析具有一定的指导和借鉴作用；文献[9]研究了热变形对涡旋盘整体变形的影响；文献[10]通过建立热力学模型对无油涡旋压缩机的研制和性能研究，具有重要的指导和借鉴作用；文献[11]推导出了二维稳态温度场的离散模型，利用RPIM对二维稳态温度场进行研究和计算。在有关涡旋齿温度分布的研究文献[2、6]中，计算涡旋齿温度分布的迭代公式计算收敛时间较长且后处理不方便。

根据传热学[12]中控制体积法构建了涡旋齿的一维非稳态传热模型，以任意位置处涡旋齿壁面的等效温度作为热边界条件；利用径向插值无网格法构建涡旋齿一维和二维稳态传热模型，运用计算软件MATLAB分别计算模拟涡旋齿的温度分布。为实验验证提供了基本的理论依据，对探究压缩过程中涡旋齿头的温度场分布情况有着重要意义。

2 利用控制体积法计算涡旋齿温度场分布

动涡旋齿的传热是移动对流边界条件下的热传导问题。以下假设是对动涡旋盘绕传热的数值研究做出的：

（1） 壁上的温度对动涡旋件的影响可忽略不计，因此绕动涡旋件的温度沿其高度是均匀的。只考虑动涡旋盘和压缩室中的工作气体之间的对流传热。

（2） 导热系数，热扩散系数和热传导系数假定为常数。

（3） 属于2个相邻压缩室的2个顶点的公共区域中的气体温度是与法线角度成线性关系。每个顶点的公共区域的长度近似等于涡齿的厚度。

（4） 动涡旋盘周围的环境温度等于相应压缩室中的理论温度。

（5） 速度对涡齿的温度影响可以忽略不计。

2.1 控制领域离散化

将问题简化成沿着X方向的一维问题后，涡旋齿齿高方向两侧齿壁就不再是计算区域的边界，此时，边界是X=0和X=L处，L为沿着圆渐开线位置进气口至出气口涡旋齿的长度，但是两侧与压缩腔中的气体是有热量的传递，而且不能忽略，此时只能将表面传递的热量折算成整个截面上的体积内热源，若向外散热，则内热源为负，若环境向涡旋齿传热，则内热源为正，最终该物理问题就变成一维非稳态有内热源的问题。一维非稳态有内热源公式

式中 ρ——热传导材料的密度，g/cm3

c——材料比热，J/（kg·K）

λ——材料热传导系数，W/（m·K）

S——非常数内热源，W/m3

对任意控制容积P假设其源项表示为

式中 Sc、SP对控制容积P均为常数，SP对为变量T的源项曲线在控制容积中P点的斜率

对于非稳态导热问题的离散方程，采用控制体积法得到。对于内部节点，节点P所代表的原体首先进行离散化，确定节点P，再确定控制容积，将L为0～1300 mm分为M+1个节点，M个控制容积，其中，得到一维控制容积如图2所示[13]。

2.2 一维非稳态热传导问题格式

考虑图2所示一维控制容积。控制容积均分，在时间t内对P做积分[13]

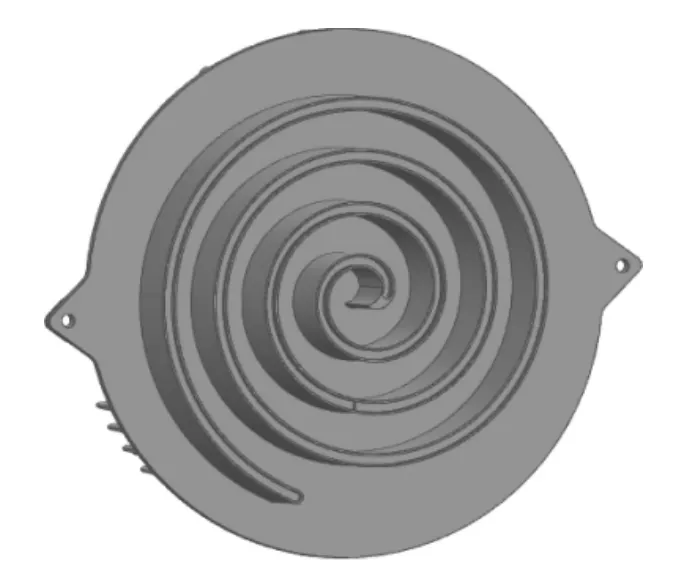
图1 动涡旋盘3D模型图

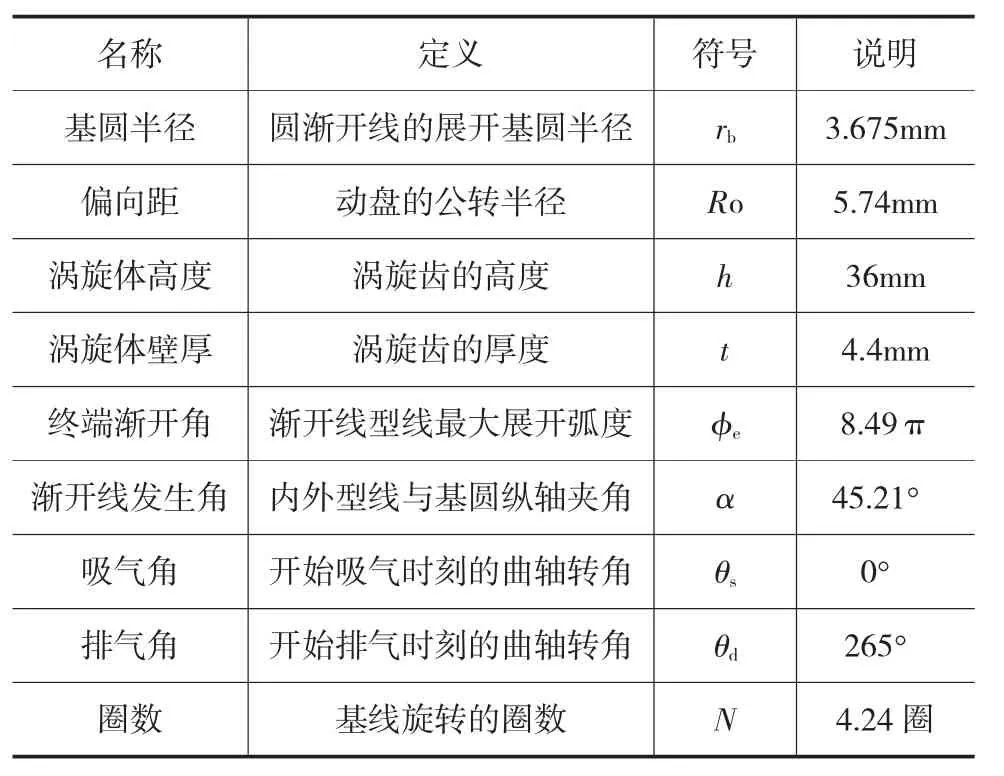
表1 涡旋压缩机几何参数

图2 一维控制容积尺度

图3 基圆和渐开线围成的面积

化简最终公式可写为

使用控制体积方法获得的方程可以表示为离散的全隐格式为

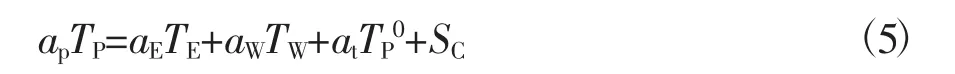
2.3 工作腔容积的计算

对该无油涡旋压缩机工作腔体的容积计算时需研究腔体的变化，即对其吸气、压缩及排气逐个腔体研究。当主轴转角0<θ<2π时，即为吸气过程；当主轴转角0<θ<θ*时，即为压缩过程；当主轴转角θ=θ*时，即为开始排气时刻，直到排气结束，一个工作周期结束。

如图3即为圆渐开线涡旋型线的示意图。任取图中的白色扇形区域记为一微元三角形，该微元三角形的一直角边与圆形弧边的边长分别为（γbφ） 和（γbφdφ），该微元三角形的面积公式，即为

则阴影部分的公式S，即为

根据微元面积公式进行推倒，可以得到任意工作腔在任意主轴转角时的容积计算公式。

（1） 吸气腔容积计算

在主轴转角θ=0°时，主轴从静止开始运动，涡旋腔打开，气体从开设在静涡旋盘上的吸气口进入吸气腔，到θ=2π时刻，压缩腔体闭合，吸气过程结束。该吸气腔的容积为

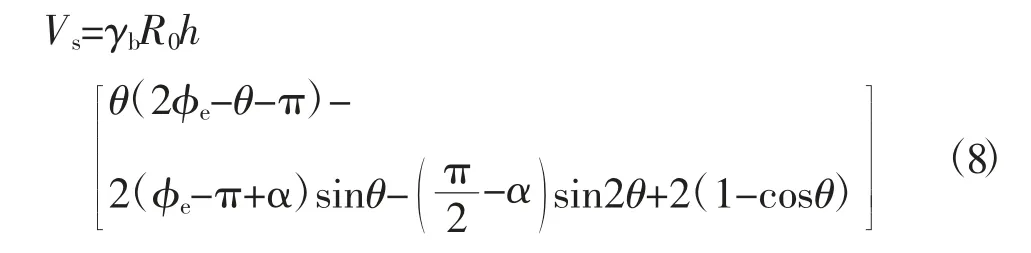
（2） 第四压缩腔容积计算

主轴转角θ∈（2π，4π）时，工作腔内气体不断被压缩并随动涡旋盘做公转平动，直至第四压缩腔，此时容积公式即为

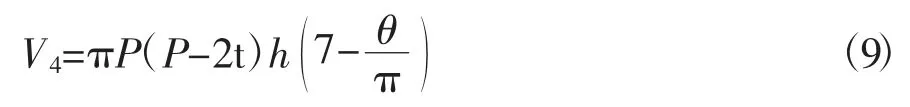
（3） 第三压缩腔容积计算

主轴转角θ=4π时，随啮合点向内转移，第四压缩腔逐渐消失并被第三压缩腔取代。此时容积公式，即为

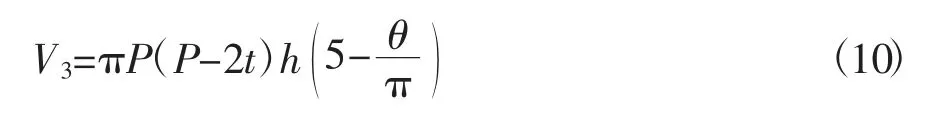
（4） 第二压缩腔容积计算

当主轴转角θ=6π时，随啮合点向内转移，第三压缩腔逐渐消失并被第二压缩腔取代。在θ∈（6π，6πθ*） 时，此时容积公式，即为

（5） 中心腔容积计算

中心腔的计算分为2个部分，此时当主轴转角θ为6π+θ*，第二压缩腔逐渐消失并被中心排气腔取代。在θ∈（6π+θ*，8π）时，第二压缩腔与中心排气腔合成同一腔体，此时中心腔容积公式，即为

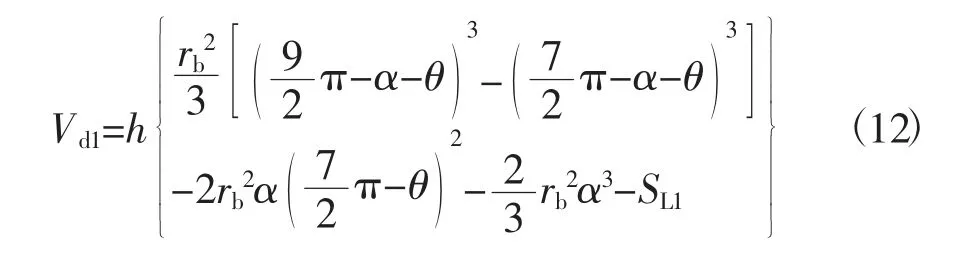
当主轴转角θ∈（8π，8π+θ*） 时，气体基本排出，此时容积公式，即为

如图4所示，为无油涡旋压缩机工作一个周期内单一腔体容积随主轴转角的变化曲线图。容积曲线整体变化为先上升到峰值后下降，上升趋势相比下降趋势较为明显。图中黑色曲线阶段为吸气过程，不难看出上升速率较高且在吸气结束前至峰值，涡旋盘持续平动，曲线末尾稍微下降是由于吸气腔未关闭时部分工质被压出腔外，红色曲线阶段为压缩过程，工质从吸气腔逐渐压缩至中心排气腔，蓝色曲线维排气过程，气体逐渐被排出，工作腔气体被压缩，容积不断下降，直至主轴转角达到排气角时刻时，随排气孔口逐渐打开，腔内的容积持续下降，直至全部排完，即容积为0，完成一个工作过程周期。

由文献[7]将涡旋齿内侧型线上任一点的气体等效温度Tf，作为热边界条件公式如下

任意转角下压缩腔的温度随转角的变化关系为[7]

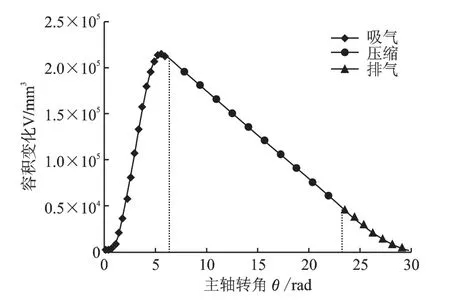
图4 容积随主轴转角的变化曲线图

表2 热力学性能

2.4 涡旋齿壁温度分布

利用Thomas算法求解一维非稳态代数方程并化简其传热模型为

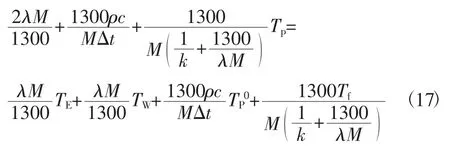
利用MATLAB对计算涡旋齿温度场的迭代公式进行编程，得到涡旋齿一维温度Ti分布如图7。

3 利用无网格法计算涡旋齿温度场分布

3.1 无网格法的基本原理

将无网格法运用到涡旋齿一维及二维温度场进行了计算分析。利用耦合径向基函数、多项式基函数构造近似函数，解决了在点插值中系数矩阵奇异性的问题，拥有插值时可以直接施加本质边界条件的优点。无网格法应用于涡旋齿的温度场的研究，目前还未见报道。将无网格法引用涡旋齿一维及二维到温度场的研究中，构建涡旋齿温度场问题的控制方程并进行离散化，施加边界条件进行计算模拟。

在二维区域内有定义公式[15]

式中 pT（x，y） ——完备多项式基

ai（x，y） ——系数，一般可以表示成为

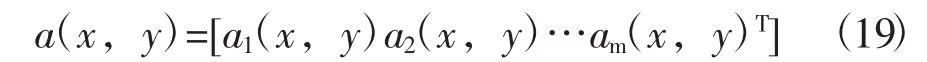
对于典型的二维温度场问题，常用的完备多项式基函数有

线性基

平方基

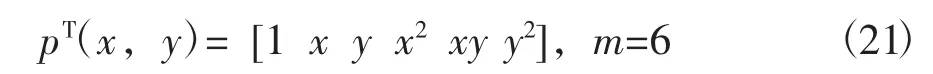
为确定系数a（x，y），在局部范围内构造带权重L2的范数

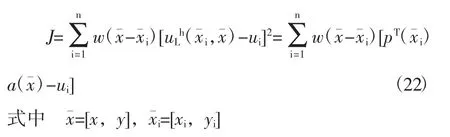
n——个数

由J取得最小值条件，可得到

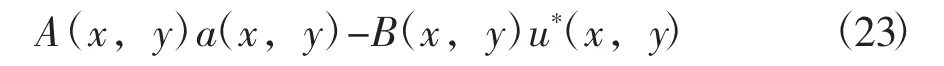
把上式代入（23），即可得最小二乘近似数

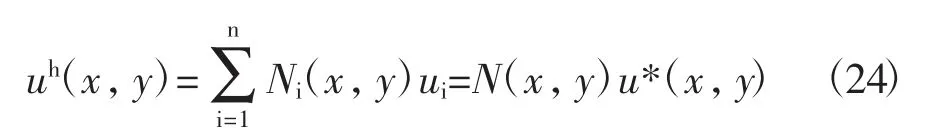
其中Ni（x，y）为形函数，且

3.2 二维温度场无网格法公式

对于工程中的典型二维稳态温度场问题，其控制方程和边界条件为[15]

即（K1+CK2）u*=p，其中

由最小二乘法移动拟合可得节点温度值

（1） 涡旋齿一维稳态温度场

将无网格法运用到解决无油涡旋压缩机涡旋齿的一维温度场中，涡旋齿的长度L 约取为1300 mm，采用高斯积分且每高斯积分段含有4个高斯积分点，计算节点数，为了保持矩阵的非奇异性，高斯积分点个数应该大于节点数，节点坐标均匀分布，确定区域高斯积分网络和坐标，确定积分点的支持域并求出支持域中节点的形函数，施加第一类边界条件求解出一维温度场。

如图5所示，涡旋齿温度分布从涡旋型线起始展角向终止展角逐渐减小，涡旋齿齿头处最高旋齿壁面温度温度达到160℃左右，涡旋齿最外圈温度为进气温度，沿涡旋齿从中心向涡旋齿外缘，其涡旋齿温度逐渐减小；涡旋盘底面的温度从涡旋中心向外缘环状递减。

这2种方法构建了涡旋齿的传热模型，得到的温度场分布如图5，其中控制体积法传热模型加入了等效温度公式，更能得到符合实际的温度场分布，但收敛速率慢；而无网格法计算温度场速率更快，而且是首次运用到涡旋齿温度场的计算中。结果均得到旋齿从中心向外缘其温度逐渐减小且在涡旋齿后段减小趋于平缓，为实验验证提供了理论依据。

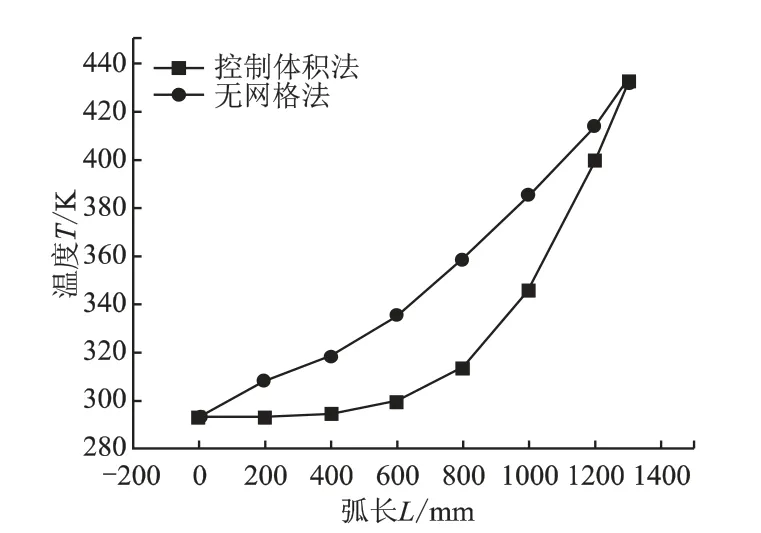
图5 涡旋齿一维温度场分布

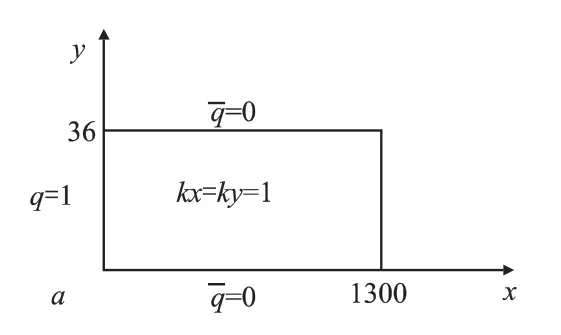
图6 二维计算平板模型

图7 涡旋齿二维稳态温度场分布

（2） 涡旋齿二维稳态温度场

利用了无网格法构建了涡旋齿的二维温度场传热模型，利用二维稳态温度场的离散模型，将涡旋齿展开视为平板，图6所视为计算平板模型，其中长为L=1300，齿高h=36，沿x=0施加恒温20℃为边界条件，沿着y=0及y=36的边界上给定一恒定温度，沿着x=1300给恒定定温度160 ℃，热传导系数kx=ky=1，在计算时，布置153（17×9） 个计算节点，背景积分网格数为16×8，每个背景积分网格采用8×8个高斯积分点，得到稳态后涡旋齿二维温度场分布如图7所示，涡旋齿的温度分布在左侧进气口变化不大，右侧出气口变化较大，出气口涡旋齿头处温度最高，清晰的显示了涡旋齿壁面二维温度场分布，为实验提供了理论基础。

4 结论

分别运用了2种方法构建及计算了无油涡旋压缩机涡旋齿的温度场，得到的结论如下：

（1） 分别利用控制体积法和无网格法建立了涡旋压缩机涡旋齿一维温度场分布模型，将等效温度法融入到传热模型中，得到了涡旋齿一维温度分布规律，并利用MATLAB计算温度场，无网格法计算效率更高，结果旋齿从中心向外缘其温度逐渐减小且在涡旋齿后段减小趋于平缓。

（2） 利用无网格法建立了涡旋齿壁面的二维稳态温度场分布传热模型，利用MATLAB计算得到齿壁面温度分布，涡旋齿的温度分布在进气口变化不大，出气口变化较大，出气口涡旋齿头处温度最高。