相机检校DLT算法的改进

孙培芪, 卜俊洲, 陶庭叶, 房兴博, 贺 晗, 冯佳琪

(合肥工业大学 土木与水利工程学院,安徽 合肥 230009)

随着近景摄影测量技术的发展以及非量测摄影机的广泛应用,由于非量测摄影机的畸变较大,需要经过畸变参数矫正才可以应用于后续的研究,越来越多的相机检校场地以及检校算法都得到了迅速的发展。其目的是利用检校场通过共线方程快速计算出非量测摄影机的内方位元素(x0,y0,f)和各种畸变参数(k1,k2,…,P1,P2,…)。传统的室内相机检校场地(如武汉大学遥感信息工程学院建立的室内检校场)环境要求较高,造价昂贵且日常维护较困难。在某些情况下,对非量测摄影机进行临时矫正并不适用。

本文提出了一种较为简便的相机检校场地建立方法,并针对该检校场对直接线性变换(direct linear transform,DLT)算法进行了相应的改进。该算法可以使检校场地的环境要求大大降低,只需要一面墙并且拥有一定的纵深,使设立的控制点保持不在同一平面即可。但是,实际情况下纵深程度往往达不到要求,使共线方程误差系数矩阵呈现病态,从而影响内方位元素以及畸变参数的精度,因此本文通过整体最小二乘方法改进的DLT算法可以解决纵深程度不够的影响,使求得的检校参数满足要求。

1 校场的建立

相机检校是非量测摄影机进行近景摄影测量的前提,其目的就是要求得相机的内方位元素、径向畸变差以及偏心畸变差,从而恢复每一张影像光束的正确形状[1]。相机检校场建立的好坏往往会决定整个近景摄影测量的结果,因此场地的建立要满足以下条件[2]:

(1) 控制场要具有一定的深度,使得布设的标志点不在一个平面上。

(2) 地面控制点的建立要有利于单片空间后方交会。

(3) 标志点所形成的控制网在一定时间内保持稳定。

(4) 所有的标志点利用全站仪在统一坐标系下进行精确量测。

1.1 检校场地的选择

在考虑以上检校场地的条件,并且满足该实验所需要的纵深程度不够的要求,场地选择了一座普通办公楼的一面墙。墙上具有排水所用的排水管,以此来作为一定程度的纵深。该墙面光照充足,可以在任何时间获取实验所需的数据,墙面整体为黄色,白色部分为反光贴。符合实验所要求的临时简易检校场的条件。建立的检校场如图1所示。

图1 简易室外检校场

1.2 标志点的选区与建立

标志点的选择应有利于图像中像点坐标的提取,而且要使全站仪方便瞄准,获得高精度的物方坐标。因此利用反射片作为标志点,反射片模板为40 mm×40 mm。其布设要求是所有的标志点不在同一平面内,并且拥有一定的纵深程度。

在实验中,为了保证纵深程度不够的要求,仅在水管上布设少量标志点,其余标志点均匀布设在墙面上。经相关试验验证[3],标志点布设9～14个,精度为最佳。故该检校场共布设10个标志点,其中3个布设在水管上,另外7个均匀布设在墙面上。

1.3 地面控制点的建立

在该检校场中,采用相对坐标进行计算。可以建立极坐标系,利用全站仪在地面布设的控制点对标志点进行量测即可获得相对坐标。首先在距离墙面5 m且正对检校场中心的位置上埋设钉子作为坐标原点,接着在距离第1颗钉子10 m处埋设第2颗,并且要求2颗钉子的连线与墙面平行。

假定钉子的延伸方向为北方向，为了防止坐标值出现负数,将原点坐标设置为(1 000,1 000,10)。使用时将全站仪架在坐标系原点且沿北方向置0,将2号钉子设立为后视点,并输入坐标(1 010,1 000,10),校核后即可对检校场标志点进行量测,获取相对坐标。

2 共线方程与整体最小二乘

2.1 相机检校的内容与误差来源

检校目的[4]如下:

(1) 对主点(x0,y0)的测定以及主距f进行测定。

(2) 光学畸变系数的测定。

数码相机进行检校主要是为了恢复影像光束的正确形状,即时获取非量测相机的内外方位元素以及光学畸变参数。光学畸变参数主要分为径向畸变与偏心畸变2种。

2.2 含有镜头畸变参数的DLT解法

2.2.1 共线方程解法

根据中心投影的相片列出的方程[5]如下:

(1)

其中,(x0,y0)为像主点坐标;(Xs,Ys,Zs)为摄影中心的坐标;(X,Y,Z)为物方坐标;(x,y)为像方坐标。

将共线方程线性化:

(2)

(2)式中有L1～L11共11个未知参数,需要根据6个物方坐标系坐标以及6个像方空间坐标列出11个方程才能解出11个未知参数。列出如下方程式:

(3)

(3)式的简化形式如下：

AL-w=0

(4)

其中,A为系数矩阵；L为参数矩阵；w为常量矩阵。

对于非量测相机来说,相机存在镜头畸变,需对镜头畸变进行改正。而解出的值由于镜头畸变只是L1～L11的近似值,故需要考虑镜头畸变的影响。含有相机镜头畸变参数的共线方程为:

(5)

(5)式中,(Δx,Δy)像点坐标为非线性改正量,具体计算公式为：

(6)

其中，k1、k2为镜头的径向畸变系数；P1、P2为镜头的偏心畸变系数。从而得到共线方程的误差改正方程为:

(7)

其中,(L1～L11,k1,k2,P1,P2)为L矩阵的参数。

A=L9X+L10Y+L11Z+1

(8)

2.2.2 L矩阵的求解

误差方程的简化形式如下：

V=BL-w

(9)

(10)

(11)

B1为B矩阵的1～4列:

B2为B矩阵的5～8列:

B3为B矩阵的9～11列:

B4为B矩阵的12～13列:

B5为B矩阵的14～15列:

从而,将(9)式变形为：

L=(BTB)-1BTw

(12)

即可获得求解L矩阵的公式。内方位元素(x0,y0,fx,fy)求解如下。

x0、y0的求解公式分别为:

(13)

(14)

fx、fy的求解公式分别为:

(15)

(16)

上述步骤是一迭代过程,其迭代判断依据是相邻2次fx之差是否小于0.01 mm。

2.3 基于奇异值分解的整体最小二乘方法

基于奇异值分解的整体最小二乘方法[6],其误差方程的表现形式为:

L=(A-EA)X-el

(17)

其中,L为n×1维观测向量;X为m×1维未知参数向量;A为n×m维观测系数矩阵;EA为A的随机误差矩阵;el为n×1维观测噪声矩阵。为了解决整体最小二乘问题,(17)式可改写为:

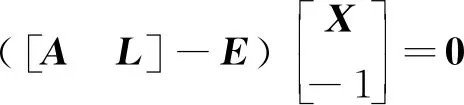
(18)

(19)

对上述SVD分解后的矩阵进行分块:

U1=[U11U12]

(20)

(21)

(22)

未知参数的最佳估值为:

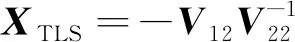
(23)

在DLT算法中,可以对[Bw]矩阵进行奇异值分解的方法进行求解L矩阵[7]。

3 应用实例

3.1 影像获取及像平面坐标提取

本文所检校的相机为佳能5D MarkⅢ相机。该相机有效像素为2 230×104,4.4倍光学变焦镜头,等效35 mm焦距为24～105 mm,并配合全新的DIGIC5+处理器,常用感光度为ISO100～25 600。该相机为非两侧摄影机,可固定焦距进行拍摄,且支持高清影像。

拍摄前,将相机放置在脚架上,通过水准气泡将相机调制水平,固定好焦距,在光线充足的情况下对检校场进行拍摄。

拍摄时,应使被摄对象基本占满整个像幅,以此来获得较大比例尺,并且每张相片尽可能多地包含标志点,这样可以尽可能地提高精度,也可以充分反映影像畸变差。

拍摄完相片之后,就要提取影像中标志点的像点坐标[8]。首先,利用PhotoShop将每个标志点的像素坐标提取出的单位设置为cm。提取坐标时,应用鼠标对十字丝进行精确定位[9]。此时由于像点坐标系的原点为相片左上角,而且x、y正方向分别为向左和向下;接着,需要将坐标原点平移到相片中心,将相片分为4个坐标系,并且将y轴方向反转,将其变换为熟悉的坐标系,此坐标系称之为像平面坐标系。标志点在相平面坐标系下的坐标为像平面坐标,也是带入共线方程所需要的数值;最后,将提取出的像点坐标根据坐标系的平移转化为像平面的坐标,其结果见表1所列。

表1 像平面坐标 cm

3.2 获取标志点物方空间坐标

本文使用海星达ATS-320全站仪,测距精度为3 mm±2 pm。在实验中,首先利用全站仪在2个地面控制点上分别架站测10个标志点,各测4次取平均值。两站测得结果相差小于1 mm,满足精度要求,再取平均值得到10个标志点的坐标[10]。

各标志点坐标见表2所列。

表2 物方空间坐标 m

3.3 实验结果

(1) 将以上数据带入共线方程,使用普通最小二乘方法求解,利用Matlab进行解算。运算结果显示误差系数矩阵接近奇异值。这正是由于检校场的纵深程度不够所造成的。

(2) 将数据带入共线方程,使用改进的整体最小二乘方法,并利用Matlab进行解算,其结果见表3所列。

表3 Matlab计算结果

(3) 使用软件对佳能5D MarkⅢ相机进行检校。将所得数据作为精确值，如图3所示，精确值与实验所得数据进行对比,见表4所列。发现实验所得结果在小数点后n位与精确值一致,从而证明该方法所得检校参数接近精确值。

图3 Lensphoto检校结果

表4 数据对比

4 结 论

(1) 本文所使用方法在一定程度上缓解了检校场纵深程度不够对检校参数的影响。检校场的建立要遵循其基本要求,即所有点不能在同一平面上,但是该方法可以完成一些场地无法满足要求的情况下的相机检校工作。

(2) 最小二乘方法其实质是对接近奇异值的矩阵进行求逆的一种近似解。其近似解的精度与精确解的差异很小,对于实际生产中所造成的影响已经微乎其微。因此利用整体最小二乘方法可以在检校场纵深程度不够的情况下,代替最小二乘求解。该方法也提供了一种建立临时简易相机检校场的方法,即使在纵深程度不够的情况下,也可得到检校参数的近似解,使工作者可以快速获取数据。

(3) 整体最小二乘方法是矩阵求逆近似解的方法之一,其他方法是否可以应用于相机检校,所得检校参数的精度是否满足要求,也是未来值得探讨的问题。

(4) 传统相机检校场地的建立需要满足的要求较高、造价昂贵以及需要日常维护。因此简易的相机检校场的建立还需要进一步的研究。