RA码与网络编码的联合设计
妙 琳,彭亚雄,陆安江
(贵州大学 大数据与信息工程学院,贵州 贵阳 550025)
近年来,网络编码的研究和应用一直受到学者的关注,物理层网络编码(Physical-layer Network Coding,PNC)[1-2]的提出解决了网络编码(Network Coding,NC)不能直接在具有广播性质的无线信道中应用的问题。PNC应用范围广泛,其在安全性[3]方面以网络编码为指导,能够提供高效、敏捷的主动保护。文献[4]利用编码的可靠性,对编码进行最优布局规划,设计应用于不同网关的传感器。网络编码技术的一个重要功能是在无线通信[5-6]中使网络性能得到提升,促进网络传输速率。NC还可应用于依赖边缘资源的新兴雾架构,以实现更高的吞吐量。文献[7~8]提出的混合编码设计方法虽然优于编码的独立方案,但是网络编码本身存在计算复杂、功耗较大的缺点,还需要进一步的研究和完善。
重复累积(Repeat-Accumulate,RA)码[9]是在Turbo码和低密度奇偶校验(Low Density Parity Check,LDPC)码基础上提出的一种信道编码,它集Turbo码和LDPC码的优越性能于一身。文献[10]的研究虽然改变了Turbo码的误比特性能,但仍存在译码算法复杂的缺陷。RA码的译码算法[11-13]中包括迭代译码、和积算法和最小和算法,在不同的情况下,随机采用不同的算法,降低了译码计算的复杂度和系统的误码性能。本文采用基于RA码的信道编码与物理层网络编码的联合设计方法,其性能优于一般的RA码和物理层网络编码,误比特率和信噪比大幅降低,系统性能优良且高效。
1 RA码的结构模型
RA码是一种具有两种不同身份的码,一类为具备编码简单性的“Turbo-like”码,另一类为译码高效性的LDPC码。如图1所示,是RA码作为一类“Turbo-like”码对应的编码结构。
1.1 RA码的编码
当RA码被看作为一类“Turbo-like”码,它的结构是一个码率为1/q的重复码与一个码率为1,传递函数为1/(1+D)的卷积码(也称累加器)经一个交织器串行级联。如果将RA码当作LDPC码时,累加器和交织器决定校验矩阵H的结构,二元RA码的编码过程如下:
信息序列m=[m1,m2,…,mk]长度为k,被重复器重复p次得
(1)
交织器参数∏=[π1,π2,…,πn](n=k×p)决定b被交织器置换后的输出序列,序列b的交织过程可表示为
D=[d1,d2,…,dn]=[bπ1,bπ2,…,bπn]
(2)
交织器输出比特序列D,D经过组合器组合。假设组合器参数为a,则将每a个比特为一组进行模2加。组合完毕后,组合器输出长为k×p/a的比特序列r=[r1,r2,…,rkp/a],其中
r1=d(i-1)×a+1⊕d(i-1)×a+2⊕…⊕di×a,i=1,2,…,k×p/a
(3)
这里“⊕”为模2加。
然后k×p/a个比特经过累加器累加,输出k×p/a个校验比特:P=[p1,p2,…,pkp/a]。累加过程可表示为
(4)
最后系统码字输出为c=[m1,…,mk,p2,…,pkp/a],码长n=k+k×p/a,码率R=k/(k+k×p/a)=
a/(a+p)。
RA码的校验矩阵H分为两个部分:H=[H1,H2],其中H1是kp/a行k列矩阵,结构由重复器、交织器和累加器决定,行重和列重分别为p和a。H2的结构由累加器决定,是一个大小为k×p/a的双对角线方阵
(5)
1.2 RA码的译码算法
RA码完成译码有两种主要的方法:一种是Turbo码译码算法,另一种是置信传播(Belief Propagation,BP)算法。下面介绍RA码的BP译码算法[14]。
令p1和p2(均为非负数)分别表示比特位为0和1的概率密度,并且p1+p2=1。在译码算法中,如图2所示,有4种不同的信息:(1)从信息节点v传向校验节点c的信息m[v,c];(2)从校验节点c传向信息节点v的信息m[c,v];(3)从校验节点c传向奇偶节点y的信息m[c,y];(4)从奇偶节点y传向校验节点c的信息m[y,c]。
接收到的比特序列的初始值为P(r)=ln(p(x=0|r)/p(x=1|r))(x为比特位节点的值)。
BP译码算法步骤如下:
步骤1初始化,令m[v,c]、m[c,v]、m[c,y]、m[y,c]均为0;
步骤2更新从奇偶节点传向校验节点的信息
(6)
步骤3更新从信息节点传向校验节点的信息
m[v,c]=∑c′m[c′,u],c′≠c,(u,c′)∈E
(7)
步骤4更新m[c,y]和m[c,v]
m[c,y]=
(8)
m[c,v]=
(9)
tanh(x)是双曲正切函数tanh(x/2)=(e-1)/(e+1)。
步骤5循环执行K次步骤2~步骤4。
计算每个信息节点的概率对数似然值s(u)=∑cm[u,c],u∈U。若s(u)<0,则将比特位u译码为1,反之译为0。
2 RA码的联合设计
针对信道编码与物理层网络编码在中高信噪比下带宽利用率低,物理层网络编码译码复杂度高的问题,本文提出了基于RA码的信道编码与物理层网络编码的联合设计。
图3是基于RA的信道编码与物理层网络编码的联合计算流程。与一般的网络编码相比较,最大的特点在于将RA译码器加入到了PNC信息计算流程中[15-16]。首先对中继节点逐符号计算PNC后验概率向量pCH[t],t=1,…,N,yR为接收信号,pCH[t]是关于第t个PNC符号CN[t]=CA[t]CB[t],其利用式(10)得到。
pCH(cA[t]⊕cB[t]|yR[t])=
(10)

(11)
然后进入累计编码译码器译码,最终输出结果为PNC信息uN[t]=uA[t]uB[t]。
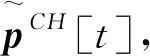
标准BP算法的消息用概率形式表示,令c为校验节点元素集合。译码的过程就是找到码字矢量x′使之满足Hx′=c。假设符号调制阶数与多元有限域阶数q相同,则解调器接收符号似然概率密度为
其中,噪声方差为σn2;调制时映射到星座图上的第a个点xa;解调器接收的第n个符号yn;接收符号yn到调制映射点xa的欧氏距离dynxa。
下面定义文中采用的变量符号:pia=p(xi=a)表示迭代前信道给出的先验信息,在迭代过程中其值不变。rjia表示校验点传给变量点关于变量节点取值为a时校验方程j的概率。qjia表示变量节点i传给校验节点j的外部概率,即在得到除j外其他所有校验节点和信道的外部信息后,判断变量节点i的值为a的概率。C(i)表示与变量节点i相连的校验节点的集合。R(j)表示与校验节点j相连的变量节点集合,R(j)/i为除i外与校验节点j相连的变量节点的集合。C(i)/j为除j外与变量节点i相连的校验节点的集合。
BP译码算法具体步骤如下:
步骤1初始化
(13)
步骤2更新校验节点信息
(14)
步骤3更新变量节点信息
(15)

步骤4尝试译码判决。
步骤5每次迭代后,计算每个码元符号的q个后验概率
(16)
第i个符号的译码判决式为
(17)
3 仿真结果与分析
基于加性高斯白噪声(Additive White Gaussian Noise,AWGN)信道,采用正交相移键控(Quadrature Phase Shift Keying,QPSK)调制,最大迭代次数为5的条件下,设置不同的相位偏移和延迟系数。然后将基于RA码的信道编码与物理层网络编码相结合,通过MATLAB实验平台进行仿真,获取误比特率(Bit Error Ratio,BER)或误帧率(Frame Error Ratio,FER)与信噪比(Signal to Noise Ratio,SNR)的性能曲线图。
仿真结果分析如下:图4所示为基于RA码的信道编码与物理层编码相结合的BER和FER曲线图。由图可知,在一定的信噪比范围内,FER呈现稳定的变化趋势,BER的值也越来越小,体现出稳定的系统传输性能。
图5和图6所示为在不同相位偏移调制下RA码的信道编码与物理层编码相结合后的BER性能曲线。可以看出,当BER=10-3时,由图5可知RA码的联合设计,QPSK调制下SNR约为5 dB;QPSK调制下信道编码的SNR约为5.4 dB;8 bit相位偏移调制下,SNR约为7 dB。由图6可知,16 bit相位偏移调制下,SNR约为8 dB;显然当RA码的信道编码与物理层编码相结合的条件下,采用QPSK调制,性能优于传统方案约0.4~3 dB,联合设计有效降低了系统的信噪比。
图7所示为不同延迟系数下RA码的信道编码与物理层编码相结合后的BER性能曲线。可以看到,当BER=10-3时,在没有延迟的情况下,RA码的联合设计后SNR约为5.35 dB。当存在有0.1T的延迟时,SNR约为5.45 dB,存在有0.2T的延迟时SNR约为6.6 dB。当信噪比SNR在2 dB左右时,3条曲线的误比特率BER几乎重合。当信噪比SNR在8~10 dB时,3条曲线的BER有相同的趋势。由此可见,在一定的延迟范围内,基于RA码的信道编码与物理层编码相结合的SNR/BER曲线变化较小,具有良好的低延迟性能。
综上所述,基于RA码的信道编码与物理层网络编码联合设计的编码技术具有低信噪比、低延迟的优良性能,并且传输系统更加稳定。
4 结束语
本文提出基于RA码的信道编码与物理层网络编码联合设计的方案。与其他传统信道编码相比,RA码的优势在于综合了Turbo码编码和LDPC码的译码的简单特性,实现了时间编码和并行译码,同时简化了物理层网络编码译码的复杂度。通过MATLAB仿真结果分析可知,RA联合设计编码技术系统的传输稳定性显著提高,系统的信噪比显著改变,且在一定延迟系数的范围内改善了系统的延迟性能。但是,联合设计编码技术只是在一定的时间内降低了延迟,今后仍需要对该技术进行提高。总体来说,联合设计编码技术的编译码算法结构简单,具有良好的系统性能和更加显著的应用优势。

