工业机器人空间轨迹仿真分析
张凯翔,陈久朋,熊彬州,李 奇,胡琼琼
(昆明理工大学 机电工程学院,云南 昆明 650500)
现阶段,机器人作为工业领域研究的热点之一,其占有量和创新性越来越成为国家综合实力的标志。运动学仿真及轨迹规划作为机器人控制的基础环节,引起了国内外学者的广泛关注。与此同时,基于MATLAB开发的机器人研究辅助工具箱也激发了相关学者极大的研究兴趣[1]。在众多MATLAB机器人仿真工具箱中,由澳大利亚Peter Corke教授开发的MATLAB Robotics Toolbox(Robotics Toolbox)是较为经典的一个工具[2],被广泛应用于机器人的辅助研究和教学示范,不仅能够获得机器人末端执行器位姿的正反解,也可以进行末端执行器的轨迹规划[3-5]。因此,作为一个强有力的辅助研究工具,Robotics Toolbox吸引了学者的广泛关注。
近年来,国内外的研究人员通过Robotics Toolbox进行了多项研究工作[6-7]。厦门大学的胡国清等学者在对柱面坐标机器人的研究中利用了该工具进行了建模与轨迹仿真,验证了所设计机器人的功能有效性[8]。哈尔滨工业大学的李瑞峰等研究人员通过该工具对仿人型机器人进行了正逆运动学的仿真,得到了双臂各关节的角度变化曲线,验证了该机器人设计参数的合理性[9]。不列颠哥伦比亚大学的Kulic′等人在对机器人的人机交互研究中,通过Robotics Toolbox进行了仿真与分析,验证了该机器人的人机交互实时安全性[10]。以上相关学者的研究工作为机器人的运动仿真开拓了新思路。但在轨迹规划方面,以点对点的轨迹为主,没有涉及对复杂的连续曲线进行仿真分析。
本文通过对Robotics Toolbox进行二次开发,增加了循环算法,使点对点的轨迹仿真扩展为连续的任意曲线仿真。同时,得到连续曲线的各关节角度、角速度和角加速度曲线。在对平面余弦曲线和空间螺旋曲线的轨迹仿真中,实时运动生成的末端轨迹与设定的目标曲线吻合,验证了该算法的有效性。
1 运动学分析
1.1 D-H参数分析
本文采用ABB_IRB120型机器人作为分析模型,该机器人具有6个自由度,行动灵活轻便,被广泛应用于电子电器、食品包装、机械加工等各个行业。该机器人具体结构如图1所示。
通过对该机器人运动单元的结构分析,建立数学模型,是对其进行运动学仿真与分析的基础。采用Denavit-Hartenberg(D-H)法对该型机器人的各个关节进行参数分析,并建立机器人的关节D-H参数表为其运动学正反解的矩阵变换提供可参考的数值依据[11-12]。首先,以该机器人的底座为基坐标系{0},其余6个坐标系依次建立在各个关节上。各坐标系均以关节转动轴为Z方向,按右手定则建立。通过对该型机器人各个关节的运动性质与运动方向的分析,建立了该型机器人的D-H空间坐标系如图2所示。
在建立的坐标系基础上,分析各关节所对应的子坐标系及其各个关节的尺寸参数[13],建立如表1所示的关节连杆D-H参数表。

表1 ABB_IRB120型机器人关节D-H参数表
其中,θ1=(-165°~165°)、θ2=(-110°~110°)、θ3=(-90°~70°)、θ4=(-160°~160°)、θ5=(-120°~120°)、θ6=(-400°~400°)。
1.2 工作空间分析
机器人的工作空间是机器人研究中的一个重要参数。工作空间受各关节的转角范围及连杆长度影响,反映了机器人的末端执行器在三维空间所能够到达的位置。通过参考机器人的D-H参数表,可分析其正向运动学的齐次变换矩阵,然后采用蒙特卡洛(Monte Carlo)法模拟出该机器人的工作空间点云图。
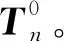
Ti=
(1)
式中,αi、ai、di和θi分别为第i个连杆所对应的连杆转角、连杆长度、连杆偏距和关节角。
将各个关节所对应的D-H参数代入式(1)中,得该机器人的末端执行器到基坐标系{0}的齐次变换矩阵如式(2)所示。
(2)
其中
m1=-S6(S4(C1C2C3-C1S2S3)+C4S1)-
C6(S5(C1C2S3+C1C2S2)+C5(S1S4-C4(C1C2C3-
C1S2S3)))
m2=S6(S5(C1C2S3+C1C3S2)+C5(S1S4-C4(C1C2C3-
C1S2S3)))-C6(S4(C1C2C3-C1S2S3)+C4S1)
m3=C5(C1C2S3+C1C3S2)-S5(S1S4-C4(C1C2C3-
C1S2S3))
px=0.072·C5(C1C2S3+C1C3S2)-0.072·S5(S1S4-
C4(C1C2C3-C1S2S3))+0.27·C1C2+0.07·C1C2C3+
0.302·C1C2S3+0.302·C1C3S2-0.07·C1S2S3
n1=S6(C1C4-S4(C2C3S1-S1S2S3))-C6(S5(C2S1S3+
C3S1S2)-C5(C4(C2C3S1-S1S2S3)+C1S4))
n2=C6(C1C4-S4(C2C3S1-S1S2S3))+S6(S5(C2S1S3+
C3S1S2)-C5(C4(C2C3S1-S1S2S3)+C1S4))
n3=C5(C2S1S3+C3S1S2)+S5(C4(C2C3S1-S1S2S3)+
C1S4)
py=0.072·C5(C2S1S3+C3S1S2)+0.072·S5(C4(C2C3S1-
S1S2S3)+C1S4)+0.27·C2S1+0.07·C2C3S1)+
0.302·C2S1S3+0.302·C3S1S2-0.07·S1S2S3)
l1=C6(S5(S2S3-C2C3)-C4C5(C2S3+C3S2))+
S4S6(C2S3+C3S2)
l2=C6S4(C2S3+C3S2)-S6(S5(S2S3-C2C3)-
C4C5(C2S3+C3S2))
l3=-C5(S2S3-C2C3)-C4S5(C2S3+C3S2)
pz=0.302·C2C3-0.302·S2S3-
0.072·C5(S2S3-C2C3)-0.27·S2-0.07·C2S3-
0.07·C3S2-0.075·C4S5(C2S3+C3S2)+0.29
式中,Si和Ci分别表示第i个关节角对应的sin(θi)和cos(θi)。由此,可根据得到的齐次变换矩阵进行正向运动学求解,得到不同关节角度变化对应的末端执行器的位姿。
采用蒙特卡洛法对机器人末端执行器的工作空间进行概率模拟,生成的工作空间三维云图如图3所示。
2 点对点轨迹仿真分析
机器人末端执行器的轨迹规划是机器人研究的重点领域之一,影响着机器人在生产制造过程中的实际使用效果。首先,根据机器人的D-H参数,使用Robotics Toolbox,通过其中的link和robot等函数[16]构建ABB_IRB120型机器人的运动学仿真模型。通过teach函数可以调出机器人的虚拟示教器。移动虚拟示教器上各关节对应的滑块,可调节仿真模型中各关节的角度,从而观察末端执行器的运动学仿真效果。
在建立的仿真模型基础上,通过Robotics Toolbox的jtraj函数[16]对末端执行器进行两点之间的轨迹规划,并生成5次多项式曲线。指定机器人末端执行器的起点与终点,起点(0.3,0,0.5)、终点(0.5,0.3,0.5)。对机器人进行点对点的末端轨迹规划,生成轨迹的效果如图4所示。
由图4可看出,机器人在所给首末点之间自动生成一条光滑的曲线。在Robotics Toolbox中求解其运动过程的角度、角速度和角加速度曲线。对其1~3关节进行分析,其关节特性参数如图5所示。
由jtraj函数自动生成的轨迹是两个关节之间的5次多项式曲线。从图5(a)中可以看出其角度曲线光滑连续。图5(b)中的角速度曲线显示其速度变化平稳。通过图5(c)中可以看出其角加速度值较小,在合理范围内[17]。
3 连续轨迹仿真分析
在实际生产制造过程中,机器人末端执行器需要加工各种不同的零件,其零件表面往往是复杂的曲面或是不规则形态。这对运动轨迹的要求远不止点对点的运动轨迹所能达到,而是需要进行复杂且连续的轨迹规划。因此,需要对Robotics Toolbox进行二次改进,使其能够进行复杂曲线的轨迹仿真。
3.1 平面正弦曲线轨迹仿真
机器人实际生产过程中,经常需要对平面进行加工。因此,对末端执行器进行平面曲线的仿真是机器人研究的重要环节。
通过在X-Z平面内绘制余弦曲线来研究各关节在平面运动的性能。余弦函数曲线的空间表达式如式(3)所示。
(3)
其曲线图形如图6所示。
要得到连续的复杂曲线,需要在曲线中设置多个中间点,让机器人执行器依次通过设定的各个中间点以完成整个复杂曲线的仿真。因此,对Robotics Toolbox进行了二次开发,通过增加循环算法,再将各个中间点之间用5次多项式连接。所得到的生成余弦曲线轨迹的仿真效果如图7所示。
由图7的轨迹生成效果图中可看出,机器人在仿真运行中按照设定的余弦轨迹路径来动作,其行走的整条轨迹与设定目标轨迹完全吻合。关节1、关节2、关节3对应的角度、角速度和角加速曲线如图8所示。
由图8中可以看出,在进行平面余弦轨迹的仿真过程中,该机器人的各关节的角度曲线连续平滑,角速度变化平缓无突变,角加速度值在较小范围内变化,各特性参数达到运动学要求。
3.2 空间螺旋曲线轨迹仿真
机器人末端执行器的空间运动轨迹是机器人运动中更为普遍的状态,也是机器人轨迹规划中的基本研究对象之一。通过在X-Y-Z空间内绘制螺旋曲线,来研究机器人的空间运动特性。其螺旋曲线的空间表达式如式(4)所示。
(4)
设定的螺旋线的空间三维模型如图9所示。
通过改进循环算法,得到生成螺旋轨迹的仿真效果如图10所示。
在图10中,机器人仿真过程中行走的轨迹与设定的目标曲线一致。其关节1、关节2、关节3的角度、角速度和角加速度曲线如图11所示。
在对上述关节运动特性图的分析中,发现关节运动的角度变化较为平滑,角度值在合理范围内。但在运动过程中存在若干点的突变情况,从而引起角速度和角加速度值的突变。经统计发现,突变点的数量占总数的4.8%以下。其原因可能是由于机器人逆解过程中的多解问题造成的[18],这也是Robotics Toolbox的一个局限性之一。在下一阶段的研究中,研究者将提出相应的优化算法来处理这种机器人逆解过程中的多解问题。
4 结束语
本文根据ABB_IRB120型机器人的结构特性,建立其运动学模型,通过MATLAB Robotics Toolbox对其进行模型仿真和点对点轨迹规划。文中对该工具箱进行二次开发,增加了循环算法,使其能够仿真复杂的连续空间曲线。同时,获得了它们运动过程中的角度、角速度和角加速度的运动特性曲线。通过对平面余弦曲线及空间螺旋曲线的轨迹进行仿真和分析,验证了该算法的可行性和有效性。在对空间螺旋曲线的速度曲线分析过程中,发现其速度存在突变情况,这是由于逆解过程中的多解性质造成的,是Robotics Toolbox的一个局限性,也是下一阶段将要研究的方向。下一阶段研究将承接本文,重点进行多解问题的优化算法研究。

