分布式存储系统中的低修复成本纠删码

张 航，刘善政，唐 聃，蔡红亮

（成都信息工程大学软件工程学院，成都 610225）

（*通信作者电子邮箱tangdan@foxmail.com）

0 引言

随着信息技术的发展，人们产生的数据越来越多，各企业为了满足人们的数据需求，纷纷搭建企业自己的数据中心并使用分布式存储系统来存储海量数据。据英特尔预测，全球数据总量在2020 年将达到44 ZB（1 ZB=109TB），而中国产生的数据量将达到8 ZB，大约占据全球总数据量的1/5［1］。在商业存储领域，数据增长极大地推动了分布式存储系统的发展。为了保障分布式存储系统海量数据的安全性和可靠性，常采用多副本［2］和纠删码［3］等容错技术。

多副本技术是将原始数据复制多份，并分别存储在不同的存储节点上。Hadoop 分布式文件系统（Hadoop Distributed File System，HDFS）［4］以及Ceph 分布式存储［5］系统均采用了多副本中常见的三副本。多副本技术操作简单，易于实施，但是该方法存储效率低。以常见的三副本为例，该方法将原始数据复制成三份，保存在三个不同的存储节点上，磁盘存储利用率仅有1/3，同时数据中心构建成本高，存储成本过大，造成严重的资源浪费。

纠删码容错技术是一种数据保护方法，它将数据分割成片段，利用编码算法生成冗余数据块存储在不同的位置，比如磁盘、存储节点上。纠删码技术相比多副本技术能以更低的存储开销存储更多的数据，Hadoop3.0 以及Ceph 分布式存储系统均采用了纠删码技术作为系统容错技术之一，同时微软的存储系统、亚马逊的AWS（Amazon Web Services）［6］等也都支持纠删码技术作为容错技术。

然而，纠删码过高的修复成本极大地限制了其技术在分布式存储系统中的实用性。纠删码在修复失效的数据块时，需要在多个节点读取数据并传输，会占用大量的网络带宽。众所周知，带宽资源一直是分布式存储系统中的稀缺资源。占用较高的网络带宽，会降低分布式存储系统的数据读取速度，从而影响到整个系统的稳定性。

纠删码的修复成本主要由其自己的特性决定，设计纠删码的编码结构能从根本上降低修复成本［7］。目前，根据编码结构的不同，关于低修复成本的纠删码的主要分为两类：分组码和再生码。分组码是将一个条带的数据块进行分组，利用组内的原始数据块生成局部冗余块，在原始数据块失效时，利用组内的局部冗余块来恢复数据块，能有效降低数据修复时需要的修复成本；再生码是通过适当增加冗余并且使新生节点从尽量多的节点下载数据块来降低修复时需要传输的数据量［8］。

Huang 等［9-10］提出了LRC（Locally Repairable Codes）、Pyramid 等典型的层次分组码。LRC 和Pyramid 码都是通过增加局部冗余的方式来降低数据块修复成本，但它们的修复成本依然过高。Facebook 采用了针对LRC 和Pyramid 上作出改进的LRCs［11］和EXPyramid［12］层次分组码。LRCs 主要针对全局冗余块再编码了一个局部冗余块，能降低全局冗余块的修复成本；EXPyramid 码是将Pyramid 码的编码数据块改为阵列结构，同时在横向和纵向两个方向编码局部冗余块，进一步降低了数据块的修复成本。林轩等［13］继续在LRC、Pyramid 的基础上提出了GRC（Group Repairable Codes）层次分组码，GRC不仅将条带进行分组生成局部冗余块，而且同时为编码条带生成局部冗余块，在数据块失效时，利用两种局部冗余块参与恢复，不需要条带中所有数据块参与修复，进一步降低了修复成本。但这三种改进方法都需要消耗大量的存储空间，并不适用大规模的分布式存储系统。Meng 等［14］提出了一种新的分组码DLRC（Dynamic Local Reconstruction Code），通过利用参数动态地调整存储开销和重构开销的平衡；但在满足多节点容错的情况下，单节点修复成本过大。Miyamae 等［15］提出了交叉分组码SHEC（Shingled Erasure Code）。SHEC 是将条带上的数据块逻辑上进行重叠并分组，进而编码出局部冗余块，在数据块失效时，利用较少的组进行局部修复，从而降低修复成本；但SHEC 重叠编码难以维持较低的修复成本和较高的容错能力，依然不适用于现有分布式存储系统。

再生码的研究主要关注MBR（Minimun Bandwidth Rrgenerating）码［16］和MSR（Minimun Storage Regenerating）码［17］。MSR 码主要拥有最低的存储开销，MBR 码主要拥有最低的数据修复成本。在2011年，Rashmi等［18］首次利用矩阵乘的方法，用统一的方法构造出MBR 码和MSR 码。Liu 等［19］提出了再生码GFR（General Functional Regenerating），通过设定一个可自由调节的参数来实现分布式存储系统的修复成本和存储成本之间的平衡，同时使用一种启发式算法来找到修复单节点失效数据的最小修复成本。Liu 等［20］同时提出了最小再生码Z 码，Z 码把置换矩阵作为元矩阵，组合构造出最优修复成本的生成矩阵，同时利用矩阵的张量乘积，迭代出任意参数下的生成矩阵，并依然保持最优修复成本。Xie等［21］提出了AZ-CODE（Availability Zones Codes），AZ-CODE 结合了MSR 码和LRC的编码方式，利用其混合优点，能有效降低修复成本。

再生码虽然可以大幅度地减少修复时的数据传输量，但在数据修复过程中，参与修复的节点需要把自己存储的所有数据都读取出来进行组合，会消耗大量的读取成本。同时，再生码编码复杂度高、编码耗时长等因素都不适用于现有的分布式存储系统。

根据数据中心对分布式存储系统故障的调查研究报告显示，其中99.75%的故障来源于分布式存储系统单节点失效［22］。因此针对现有的分布式存储系统中频繁的单节点失效且纠删码修复成本过高的问题，提出了一种低修复成本纠删码——旋转分组修复码（Rotation Group Repairable Codes，RGRC），并验证了低成本修复性。RGRC 是将条带组合成条带集，对条带集内的数据块进行分层旋转编码来减少大容量单节点失效的修复带宽。同时RGRC 在解决单节点修复成本高的问题时，依然保留着较高的容错能力，且为满足分布式存储系统的不同需求，可以灵活地权衡其存储开销和修复成本。

1 分布式存储系统中纠删码的相关概念

分布式存储系统使用纠删码作为容错技术，能消耗更少的存储空间，从而减少存储硬件的使用，大幅降低存储中心的构建成本。可见，纠删码空间利用率高的特点在存储海量数据时具有重大意义。

纠删码技术主要是通过纠删码算法将原始的数据块进行编码得到冗余块，并将原始数据块和冗余块一并存储起来，以达到容错的目的。用(n，k)表示一个纠删码，K个原始数据块D1，D2，…，DK经过计算产生了n个块P1，P2，…，Pn，这一过程称为编码。当P1，P2，…，Pn中失效的块小于该纠删码最大的容错个数时，可以选取其中剩余的块计算恢复出失效块，这一过程称为解码。相关原理如图1所示。

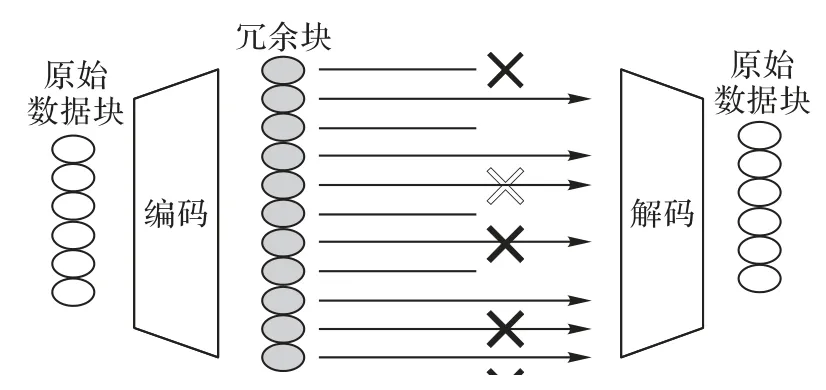
图1 编码、解码示意图Fig.1 Schematic diagram of encoding and decoding

为了便于理解，现结合图2 给出如下一些纠删码常用的基本概念的说明和定义：

1）极大距离可分（Maximum Distance Separable，MDS）码：这一类码在消耗相同存储开销的情况下，有最优的容错能力，因此被分布式存储系统广泛使用。对于一个参数为(n，k)的MDS纠删码来讲，容错能力为n-k。

2）系统性纠删码：数据块经过计算产生的块中包含原始的数据块，因良好的访问性能而成为分布式存储系统的首选。

3）容错度：纠删码可以容忍的丢失数据块个数。

4）原始数据块：用户上传的原始数据对象被系统划分后得到的块。

5）冗余块：数据块经过纠删码算法后产生的所有块。

6）条带：由多个数据块和冗余块组成，满足同一纠删码算法。

7）条带集：由多个条带组成的集合。

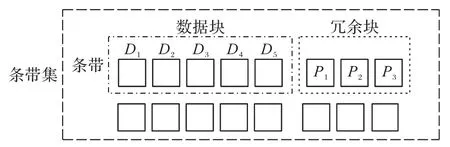
图2 数据块、冗余块、条带和条带集之间的相互关系Fig.2 Correlation between data blocks，redundant blocks，stripes and strip set

2 旋转分组修复码

2.1 纠删码数据修复问题定义

为了便于理解，基于文献给出纠删码数据修复问题相关的定义。

定义1纠删码修复成本。纠删码在进行数据修复过程中需要读取的数据量。在分布式存储系统中，网络带宽资源一直是稀缺资源，在修复的过程中读取的数据量越小，传输的数据量就小，占用的网络带宽的资源就越少，从而避免了修复过程对分布式存储系统中其他任务的影响，提升了系统的稳定性。

定义2纠删码的修复时间。纠删码在进行数据修复时所消耗的时长。分布式存储系统中，修复的快慢直接影响到系统的稳定性，如果在数据量庞大的存储系统中，一旦不能快速恢复数据，有可能导致在修复过程中因其他任务的影响而使其余数据块再次失效，因此，对于分布式存储系统中的纠删码来说，修复时间应该越小越好。

定义3纠删码的修复率。修复率是纠删码重要的指标之一。不同失效节点数时的修复率侧面反映出了该纠删码的容错能力。

定义4全局冗余块。条带中所有原始数据块参与编码计算得到的冗余块。

定义5局部冗余块。条带中组内原始数据块参与编码计算得到的冗余块。

表1为常用符号说明。

表1 常用符号Tab.1 Common symbols

2.2 编码算法

本文提出的RGRC是在系统型MDS码上作出改进的一种分组纠删码，所以本节先介绍系统型MDS 码的编码过程，然后介绍RGRC的编码过程，最后举例演示RGRC的编码过程。

系统型MDS 码的编码过程为：首先在有限域上构造编码矩阵，编码矩阵与原始数据块在有限域中执行乘法运算得到编码块。

如编码公式（1）所示，D1，D2，…，DK总共K个原始数据块与编码矩阵相乘，计算产生了C1，C2，…，Cn，共n个块，其中产生的n个块中包含了k个原始数据块。

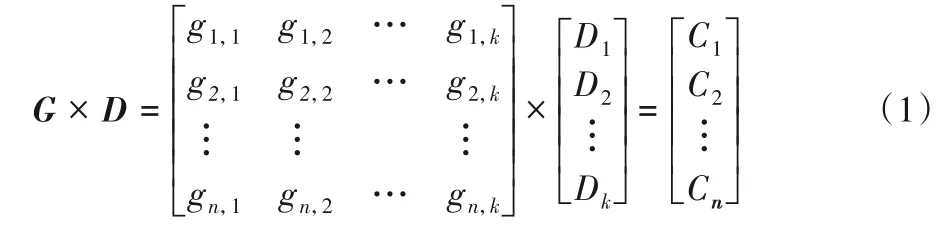
RGRC的编码过程如下：

步骤1 根据系统性MDS 码的编码方式，生成m个全局冗余块表示成P1，P2，…，Pm，记为Pi(i=1，2，…，m)。数据条带分为L个小组，记为Li(i=1，2，…，l；0 ＜l＜k），每个小组包含k0个原始数据块。保持纠删码前m0个全局冗余块不变，为每个小组计算ml=m-m0个组内局部冗余块（其中m1≥3），假设每个组内前m1-2 个局部冗余块称为R，小组Li的组内局部冗余块Ri(i=1，2，…，ml-2)的计算方法和Pi一样，只是将其他数据块置0。

步骤2 多个条带组合成条带集，形成每个条带集包含S个条带，每个条带包含L个小组的结构。小组Li的倒数第二个组内局部冗余块称为前段冗余块（Rotation Front block，RF），最后一个组内局部冗余块称为后段冗余块（Rotation Back block，RB），RF 通过前段数据旋转编码方式得到，RB 的通过后段数据旋转编码得到。相应的编码结构如图3所示。

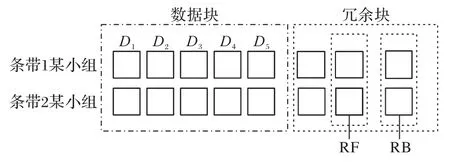
图3 RF、RB示意图Fig.3 Schematic diagram of RF and RB

步骤3Li小组内包含k0个原始数据块，设前t个原始数据块为前段数据块，其中0 ＜t＜k0，则t1=k0-t个原始数据块为后段数据块。前段数据旋转编码方式以条带集为编码单位。取每个小组前t个原始数据块，加上前一个条带内同一位置小组内的后段数据块组合成新的数据块集合，用新的数据块集合参与编码计算，计算方法和Pi一样，只是将其他数据块置0。后段数据旋转编码方式与前段数据旋转编码类似，只不过新的数据块集合由该小组的后段数据块加上前一个条带内同一位置小组内的前段数据块组成。

所有类型的冗余块编码公式如下。

1）全局冗余块生成公式：

2）组内局部冗余块生成公式：

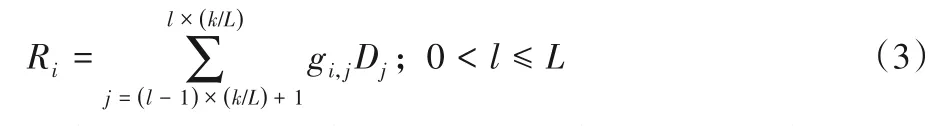
设条带集包含S个条带，RFs，l表示条带集中第s条带中第l小组的前段冗余块，RBs，l表示条带集中第s条带中第l小组的后段冗余块。

3）前段、后段冗余块生成公式如下：

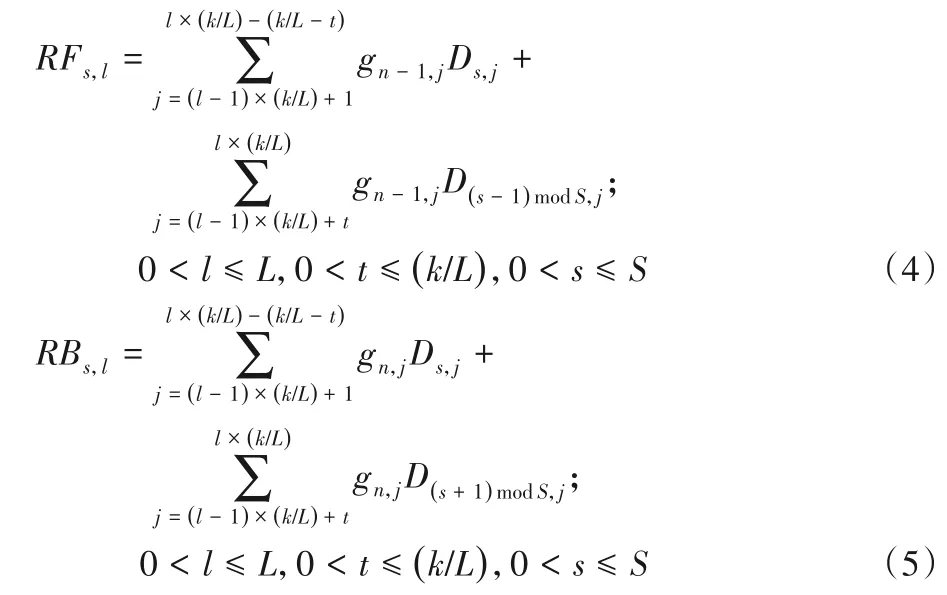
下面从(14，10)的MDS码出发，构造(18，10)RGRC演示编码过程。图4 展示的(14，10)的编码结构，D1，D2，…，D10为10个原始数据块，P1，P2，…，P4为经过编码计算后产生的4个全局冗余块。

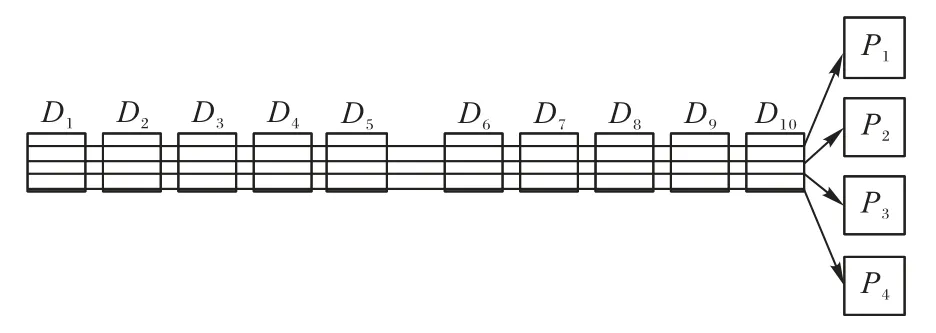
图4 (14，10)MDS码的编码结构Fig.4 Encoding structure of(14，10)MDS code

如图5所示，将MDS码的10个原始数据块分成2个小组，每个小组包含5 个原始数据块，其中L1={D1，D2，D3，D4，D5}L2={D6，D7，D8，D9，D10}，保持1 个全局冗余块不变，则每个小组产生的组内局部冗余块个数为3。L1组的局部冗余块为{P21，P31，P41}，L2组的局部冗余块为{P22，P32，P42}。

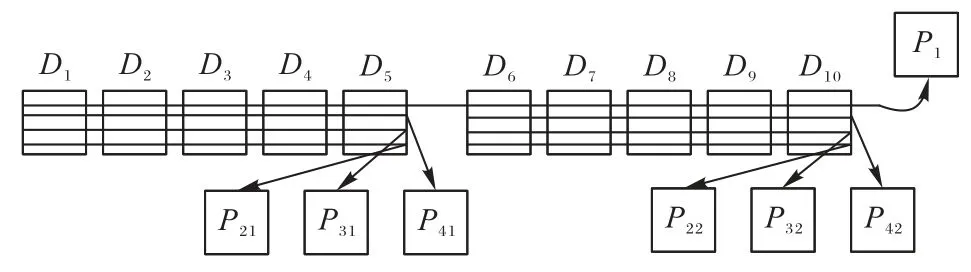
图5 条带分组后局部冗余块的编码Fig.5 Encoding of local redundant blocks after strip grouping

如图6 所示，将4 个条带组合成条带集，以第一个小组为例。设t=2，则D1、D2列为前段数据块列，D3、D4、D5列为后段数据块列。P31列为前段冗余块列。按照RFs，l生成公式构造出如图6的前段冗余块。

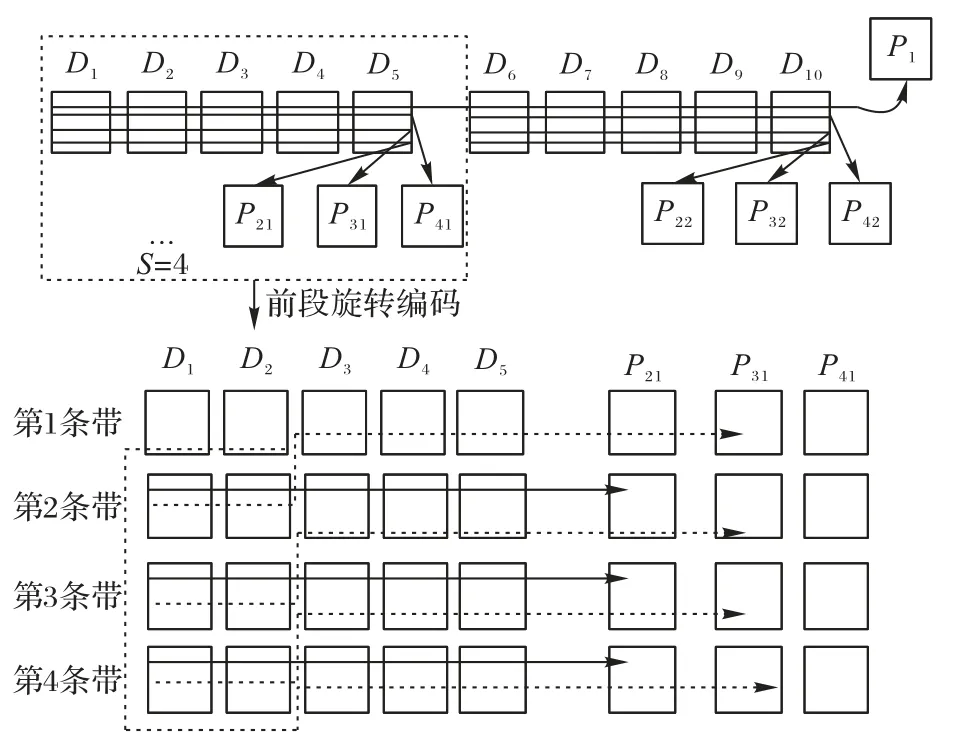
图6 前段旋转编码结构Fig.6 Anterior rotary coding structure

如图7 所示，P41为后段冗余块列。按照RBs，l生成公式构造出如图7的后段冗余块。

图7 后段旋转编码结构Fig.7 Posterior rotary coding structure

相较于MDS 码，RGRC 先通过对数据条带进行分组产生组内局部冗余块，组合条带构成条带集进行旋转编码，这种设计可以保障在单节点失效时快速在组内恢复，同时以条带集为单位进行恢复，大幅减少修复需要读取的数据量，从而降低修复时的修复成本和数据传输量。

2.3 解码算法

RGRC 的解码过程大致为：利用现有数据组合出对应的剩余编码矩阵的逆矩阵与剩余活跃的块在有限域中进行乘法运算，从而求得丢失的数据块。

在进行解码时，单节点失效虽然在节点故障中占比大，但是多节点失效在分布式存储系统中并不少见，因此，本文针对RGRC的解码分为单节点解码和多节点解码。

2.3.1 单节点解码步骤

当失效节点为单节点时，以条带集为单位进行解码。假设失效单节点在Li组，且S为偶数时，解码过程按如下步骤进行解码：

步骤1 条带集以2 个条带进行集合划分Ai={Sq，Sp}，（其中i=1，2，…，S/2），Sq、Sp为旋转编码相关联的两个条带。

步骤2 当失效节点在前段数据块列时，恢复Sq条带中的失效数据块时，读取Sq条带中Li组的前k0个未失效的原始数据块和局部冗余块组成新的块集合，并保存在缓存中。恢复Sp条带中的失效数据块时，读取Sp条带中Li组的未失效的前段数据块，前段旋转编码产生的RF块和缓存中需用到的块组成新的块集合。新的块集合和对应的剩余编码矩阵的逆矩阵相乘来恢复2 个条带中的失效数据块。照此方法循环迭代，恢复条带集中所有的失效数据块，并进一步恢复整个节点失效的数据块。

步骤3 当失效节点在后段数据块列时，恢复Sq条带中的失效数据块，读取Sq条带中Li组的前k0个未失效的原始数据块和局部冗余块组成新的数据块集合，并保存在缓存中。恢复Sp条带中的失效数据块时，读取Sp条带中Li组的未失效的后段数据块，后段旋转编码产生的RB块和缓存中需用到的块组成新的块集合。

新的块集合和对应的剩余编码矩阵的逆矩阵相乘来恢复2 个条带中的失效数据块。照此方法循环迭代，恢复条带集中所有的失效数据块，并进一步恢复整个节点失效的数据块。

假设失效单节点在Li组，且S为奇数时，解码过程按如下步骤进行解码：

步骤1 条带集以2 个条带进行集合划分Ai={Sq，Sp}（其中i=1，2，…，(S-1)/2），B={SS}，Sq、Sp为旋转编码相关联的两个条带，SS为条带集中最后一个条带。

步骤2 恢复Ai集合与S为偶数时一样。恢复B集合中的失效数据块时，读取SS条带中Li组的前k0个未失效的原始数据块和局部冗余块组成新的块集合，新的块集合和对应的剩余编码矩阵的逆矩阵相乘来恢复失效数据块。

下面以(18，10)，S=4 的RGRC 在L1组单节点失效为例，演示其解码过程。图8 中阴影表示数据块失效。条带集以2个条带进行集合划分A1={S1，S2}，A2={S3，S4}。在A1中恢复第1 条带的D1块，需读取第1 个条带的(D2，D3，D4，D5，P21)5 个块；恢复第2 条带的D1块，需读取第2 个条带的D2和第一条带的P31共计两个块。A2集合恢复失效块方法和A1一样。相较于(14，10)的MDS 码恢复4 个条带的D1列失效需读取40块，RGRC 只需读取14 块数据，比MDS 码相比修复成本降低65%。

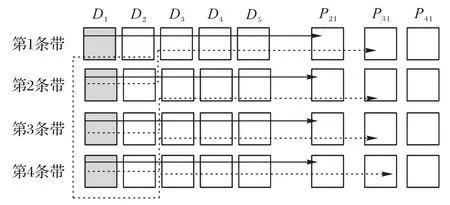
图8 单节点失效解码Fig.8 Decoding of single-node failure

2.3.2 多节点解码步骤

RGRC 与MDS 码有所区别，并不满足当失效块个数大于n-k则不能恢复，而是某些情况下当失效块数大于n-k依然可以恢复。基于RGRC 的特征，本文提出了贪心策略的解码算法，该解码算法分为2 类解码：条带集组解码、条带集全局解码。

条带集组解码是指利用和失效节点在同一小组内的条带集中未失效的块来解码恢复失效块。由于条带集中小组内块数较少，在恢复失效块时需读取的块数较少，解码成本能降到最低。当条带集组内解码无法恢复失效块时，使用条带集全局解码恢复失效块。条带集全局解码利用条带集内全局未失效块来恢复失效块，为了降低读取成本，当利用条带集全局解码恢复出某些失效块后，为可以满足条带集组解码条件时，条带集全局解码应马上转换成条带集组解码进行解码。

根据以上原则，对多节点失效的贪心策略的解码算法过程分为两个阶段：

1）条带集组解码。对于条带集中每个小组，当失效块数小于局部冗余块数，则启用条带集组解码恢复数据，当解码成功后，标记为活跃块，可以参与下一步的解码。若失效块全部解码成功完全恢复，则程序结束。

2）条带集全局解码。当失效块不能被条带集组解码恢复数据时，则启用条带集全局解码，并标记条带集中未失效块为活跃块。在全局层面，如果条带集内每个条带的活跃块大于失效块个数，则解码条带集中每个条带同一位置的失效块，并标记为活跃。同时检查可否进入第一阶段条带集组解码：如果可以，则转入第一阶段解码；若不行，程序结束。

多节点解码算法根据RGRC 的编码特点设计，条带集组解码优先，在条带集组解码失效后，再转换成条带集全局解码，一旦系统检查满足组内解码条件，再转换成条带集组解码。这种方式保证了在解码过称中读取的数据量较少，大幅减少系统的修复成本，同时将修复时间降到最低。

2.4 修复率分析

修复率是衡量一个纠删码性能的重要指标之一。在本小节中用于测试纠删码修复率的方法如下：

假设一个参数为(n，k)的纠删码，在分布式存储系统中，由于硬盘发生故障，失效的节点个数为x，根据概率学，共有种失效方式，在这些失效方式中，能够修复的失效方式和全部失效方式的比值则为该纠删码失效x节点的修复率。不同失效节点数时的修复率侧面反映出了该纠删码的容错能力。

表2 为不同参数下RGRC 在多节点失效时修复率和容错能力。从表2 可以看出在数据块个数不变的情况下，冗余块个数越多，RGRC的容错能力就越强，多节点失效时的修复率也越高。此外，冗余块个数越接近数据块个数时，相应修复节点的修复率也将越高。由表2 可知RGRC 的容错能力以及修复率可以满足大部分分布式存储系统的需求，可以根据具体的业务情况，合理地定制不同参数下的编码方案。

表2 RGRC的修复能力Tab.2 Repair capability of RGRC

图9 展示的分别是(14，10)的RS（Reed-Solomon）码［23］、(10，2，3)的LRC、(17，10)的basic-Pyamid 码、(10，2，4，3)的DLRC、(10，2，3) 的 pLRC （proactive Locally Repairable Codes）［24］、(17，10) 的 GRC、(3，3，3)，ρ=1 的 UFP-LRC（Unequal Failure Protection based Local Reconstruction Code）［25］与(17，10)的RGRC的修复率对比；在失效节点数为4时，所有的纠删码都可以完全修复；当失效节点数为5 时，(14，10)RS 码数据丢失；当失效节点数为6 时，(10，2，3)LRC、(10，2，3)pLRC 数据丢失；当失效节点数为7 时，(3，3，3)，ρ=1的UFP-LRC 数据丢失，而RGRC 依然保持着较高的修复率。而RGRC因为和basic-Pyamid码消耗的冗余存储空间一样，所以它们的容错能力和修复率几乎一样。综合来说，(17，10)RGRC 的容错能力和修复率均强于(14，10)的RS 码、(10，2，3) 的LRC、(10，2，4，3) 的DLRC、(10，2，3) 的pLRC、(17，10)的GRC和(3，3，3)，ρ=1的UFP-LRC。

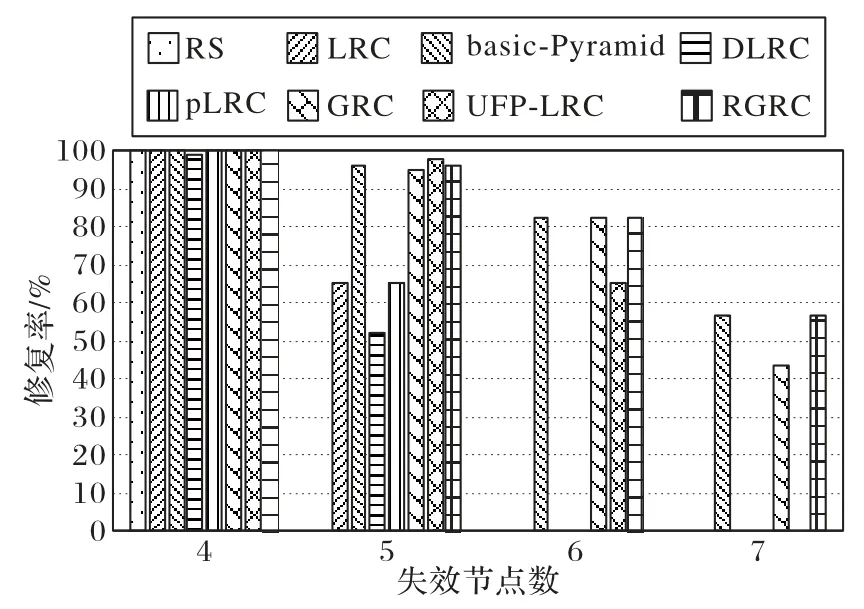
图9 修复率对比Fig.9 Comparison of repair rate

3 实验与结果分析

为了在真实的分布式环境下对RGRC 的各方面进行测试，并与现在常用的纠删码进行比较，基于Ceph 分布式存储系统搭建了纠删码测试平台。纠删码测试平台系统主要分为三个部分，分别为OSD（Object Storage Device）存储节点、Monitor 监测节点以及客户端。OSD 节点负责存储数据、恢复数据、平衡数据，Monitor 负责监视集群的健康状态以及控制集群节点相关操作，客户端用于提供用户操作集群界面。纠删码测试平台体系结构如图10所示。

3.1 实验环境

实验使用的纠删码测试平台包含20个节点，包括：1个客户端、1 个Monitor 节点和18 个OSD 存储节点。每个节点的机器参数为：CPU Intel Core i7、内存8 GB、磁盘500 GB，所有节点安装Centos 7系统和Python 2.7运行环境。

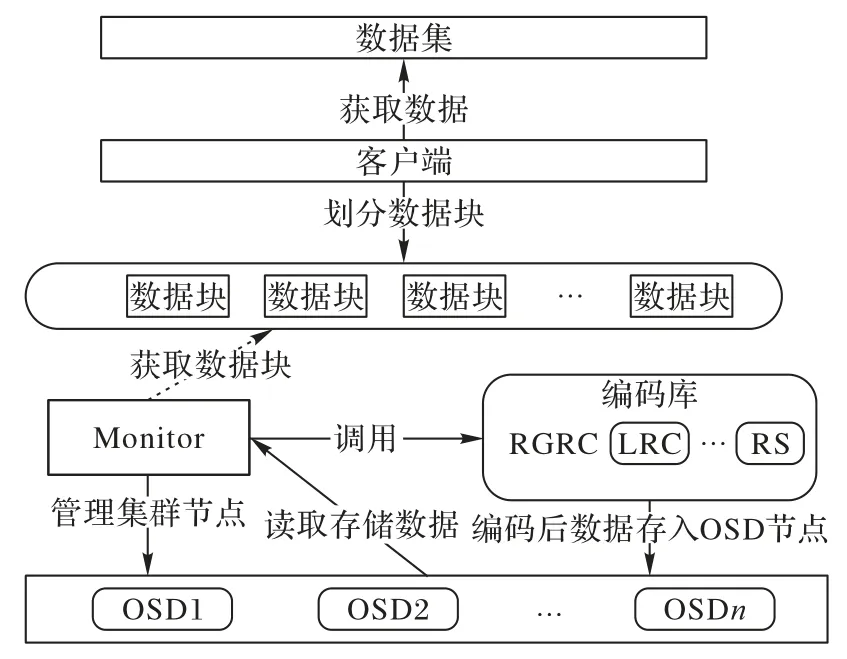
图10 纠删码测试平台体系结构Fig.10 Erasure code test platform architecture

3.2 实验对比指标和方法

实验对比指标有修复成本、修复时间和存储开销。修复成本指修复过程中实际的数据读取量，也反映修复操作对网络带宽资源的占用情况；修复时间指修复过程的快慢，反映出算法的实时能力；存储开销指原始文件经纠删码算法计算后实际存储所占用的存储空间，存储开销越小，分布式存储系统的可靠性越好。针对以上实验对比指标，根据单节点修复和多节点修复两种情况分别设计实验来监测和统计其数据。

3.2.1 修复成本实验

1）单节点失效修复成本测试。

实验设计为随机单节点故障来模拟实际应用中的节点故障规律。上传至纠删码测试平台的测试文件大小分别为1 MB～10 MB 依次递增，数据块默认大小为1 KB。读取纠删码测试平台记录的各个纠删码修复读取的数据量进行对比。

2）多节点修复成本测试。

实验设计为随机生成失效节点，假设失效节点个数为x，且x不断增大。根据纠删码测试平台记录的每次失效x节点时用于恢复所需要的数据读取量进行对比。实验用的测试文件大小为10 MB，数据块默认大小为1 KB。

3.2.2 修复时间实验

1）单节点失效修复时间实验。

实验设计为以10 MB 的存储数据作为测试数据，数据块分块大小默认为1 KB，分别设置10次单节点失效数据修复测试，读取纠删码测试平台记录的各个纠删码修复时间进行对比。

2）多节点失效修复时间实验。

实验设计为以10 MB 的存储数据作为测试数据，数据块分块大小默认为1 KB，分别设置随机不同失效节点个数情况下的数据修复测试，读取纠删码测试平台记录的各个纠删码修复时间进行对比。

3.2.3 存储开销实验

实验分别上传10 MB、25 MB、50 MB 的文件至纠删码测试平台，统计平台记录的各个纠删码在节点中占据的实际存储空间进行对比测试。

为了探究数据块和冗余块个数对RGRC 的容错能力和单节点修复成本的影响，分别使用不同编码方案的RGRC 测试其容错能力和单节点修复成本。

3.3 实验对比纠删码

实验中对比的纠删码分别是(14，10)的RS码、(10，2，3)的LRC、(17，10) 的basic-Pyamid 码、(10，2，4，3) 的DLRC、(10，2，3) 的 pLRC、(17，10) 的 GRC 和(3，3，3)，ρ=1 的UFP-LRC。(10，2，3)的LRC 和pLRC 初始都将原始数据块分成两组，每组产生1 个组内局部冗余块，为整个数据条带生成3 个全局冗余块；(17，10)basic-Pyamid 码将原始数据块分为2个小组，每组产生3 个组内局部冗余块，为整个数据条带生成1 个全局冗余块；(10，2，4，3)的DLRC 为整个数据条带生成2个全局冗余块，将总共12 个块分成3 组，每组产生1 个组内局部冗余块；(17，10)的GRC 将原始数据块分成2组，每组产生2个组内局部冗余块，为整个数据条带生成2 个全局冗余块，同时2 个全局冗余块生成1 个额外冗余块；(3，3，3)，ρ=1 的UFP-LRC将原始数据块分成3个组，每组产生1个组内局部冗余块，为整个数据条带生成3 个全局冗余块；(17，10)RGRC 将原始数据块分成2 组，每组产生3 个组内局部冗余块，为整个数据条带生成1个全局冗余块。

3.4 实验结果和分析

3.4.1 单节点修复

1）单节点修复成本实验。

图11 为单节点失效平均修复成本对比，修复成本为单节点失效恢复需要的平均数据读取量。RGRC 因在修复多条带单节点失效时，只需读取少量组内数据块和组内局部冗余块，同时可以利用缓存中的块数据，使得RGRC 的修复成本可以大幅度减少，从图11 可知(17，10)RGRC 相较于(14，10)RS 码修复成本约降低61.8%，相较于(10，2，3)LRC 修复成本约降低36.4%，相较于(17，10)basic-Pyamid 码修复成本约降低29.4%，相较于(10，2，4，3)DLRC 修复成本约降低25.3%，相较于(17，10)GRC 修复成本约降低29.5%，相较于(3，3，3)，ρ=1UFP-LR 码修复成本约降低14.8%。pLRC 虽然修复单节点时会转换成(2，1)模式进行修复来降低修复成本，但前期需要读取数据块进行转移，间接增加了其修复成本，综合pLRC 码前期转移数据块的读取成本和后期修复时的读取成本，(17，10)RGRC 相较于(10，2，3)pLRC 修复成本约降低57.6%。另一方面，由于RGRC 的修复成本与条带数量相关，随着上传文件数据量的增大，相应条带变多，其单节点修复成本相较于RS 码、LRC、basic-Pyamid 码、DLRC、pLRC、GRC、UFP-LRC将会进一步降低。

2）单节点修复时间实验。

图12为单节点平均修复时间对比。

RGRC 恢复时读取的块数量较少，修复成本缩减，同时单节点失效解码结构简单，相比其他纠删码能大幅减少修复时间。从图12 可知，(17，10)RGRC 相较于(14，10)RS 码修复时间约减少58.7%，相较于(10，2，3)LRC 修复时间约减少34.6%，相较于(17，10)basic-Pyamid 码修复时间约减少30.2%，相较于(10，2，4，3)DLRC 修复时间约减少14.2%，相较于(10，2，3)pLRC 修复时间约减少53.2%，相较于(17，10)GRC 修复时间约减少 33.1%，相较于(3，3，3)，ρ=1UFP-LRC修复时间约减少23.6%。

图11 单节点失效时各纠删码的平均修复成本对比Fig.11 Comparison of average repair cost of different erasure codes with single-node failure

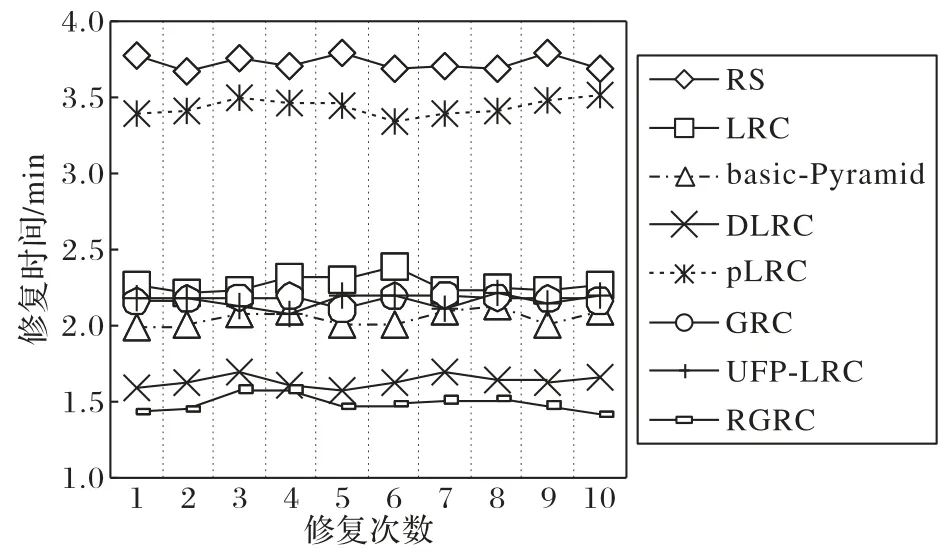
图12 各纠删码码的单节点平均修复时间对比Fig.12 Comparison of average repair time of single node by different erasure codes

3.4.2 多节点修复

1）多节点修复成本实验。

图13 为多节点失效的平均修复成本对比，修复成本为节点失效恢复需要的平均数据读取量。由于随着失效节点个数的增多，横向对比的码会超出自身的容错能力，因此，实验设计节点最大失效个数为4，来测试其平均修复成本。

RGRC 在修复单节点失效时，可以利用分层旋转编码的方式大幅降低修复成本。在修复多个节点失效时，由于牵涉到组解码恢复和全局解码恢复，修复成本会相应增多，低修复成本优势会逐渐减小。但综合平均修复成本，进行多节点修复时，RGRC 的修复成本相较于RS 码、LRC、basic-Pyamid 码、DLRC、pLRC、GRC、UFP-LRC依然是有所减少的。

2）多节点修复时间实验。

图14为多节点失效的平均修复时间对比。从图14可知，单节点修复时RGRC 的修复时间最少，随着节点失效个数的增加，相应的修复时间逐渐增加，相较于其他纠删码，其优势逐渐变小。综合平均修复时间，相较于RS 码、LRC、basic-Pyamid码、DLRC、pLRC、GRC、UFP-LRC，RGRC在多节点时的修复时间，虽不及单节点的幅度，但依然是有所减少的。

分布式存储系统中大多数的故障来源于单节点失效，快速修复单节点失效可以有效降低存储系统中多节点失效情况。由于本次设计的纠删码主要对单节点修复进行改良，降低其修复成本和修复时间。因此，相较于单节点修复实验，RGRC 在多节点的修复成本和修复时间无法达到单节点修复的降低幅度，关于多节点修复的改良将会在下一步的研究中进一步展开。

图13 各纠删码的多节点失效平均修复成本对比Fig.13 Comparison of average repair cost of multi-node failure by different erasure codes

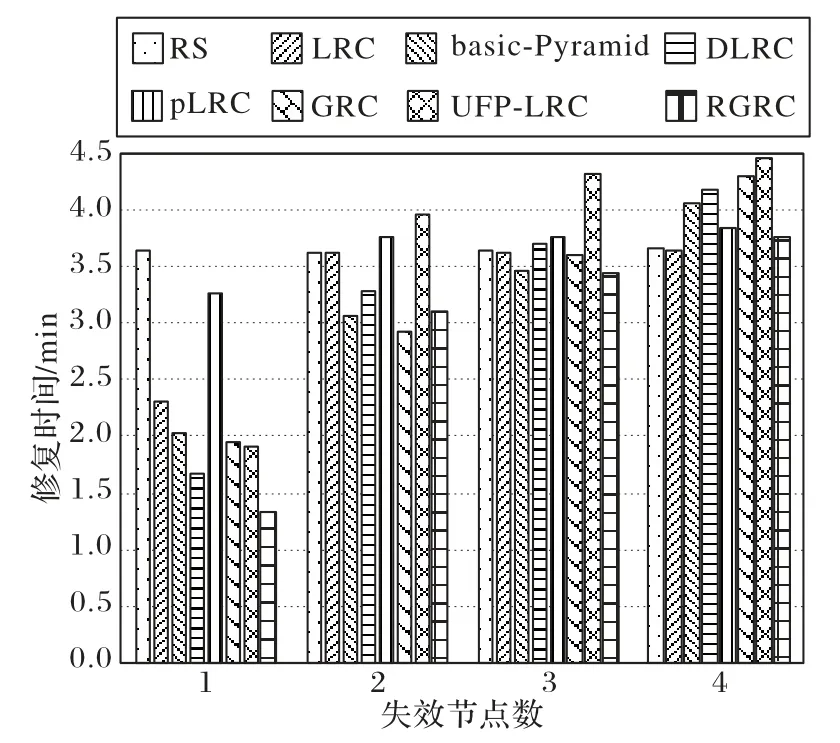
图14 各纠删码的多节点平均修复时间对比Fig.14 Comparison of average repair time of multiple nodes by different erasure codes

3.4.3 存储开销实验

RGRC 因为其旋转编码方式，能降低单节点修复成本，减少修复时间，但却消耗了一定的存储空间。图15 为纠删码存储开销对比。从图15 可知，(17，10)RGRC 相较于(14，10)RS码存储开销约增加 21%，相较于(10，2，3)LRC、(10，2，3)pLRC、(10，2，4，3)DLRC 和(3，3，3)，ρ=1 的UFP-LRC 存储开销约增加13%，相较于(17，10)basic-Pyamid码和（17，10）GRC 不增加额外的存储开销。根据实验数据的对比，虽然增加了一定的存储开销，但相比其降低的修复成本和减少的修复时间，仍可在接受的范围内。

图16 展示了不同参数下的RGRC 的最大容错能力。从图16 可以看出RGRC 的容错能力与冗余块个数有关，随着冗余块个数的增加，RGRC相应的容错能力也会随着增加。

实验结果显示，RGRC 在单节点修复时，相较于对照的其他纠删码能大幅度降低修复成本和修复时间。在多节点的修复时，随着节点个数的增加，优化幅度逐渐减小，但综合在多个节点修复时的修复成本和修复时间后，RGRC 的修复成本和修复时间依然有所改善。虽然RGRC 增加了额外的存储开销，但其本身的修复能力增强，最大容错个数以及多节点修复率都有所提高。综合来说，RGRC 通过增加冗余同时利用分层旋转编码的方式，改善修复能力、修复成本和修复时间是行之有效的。

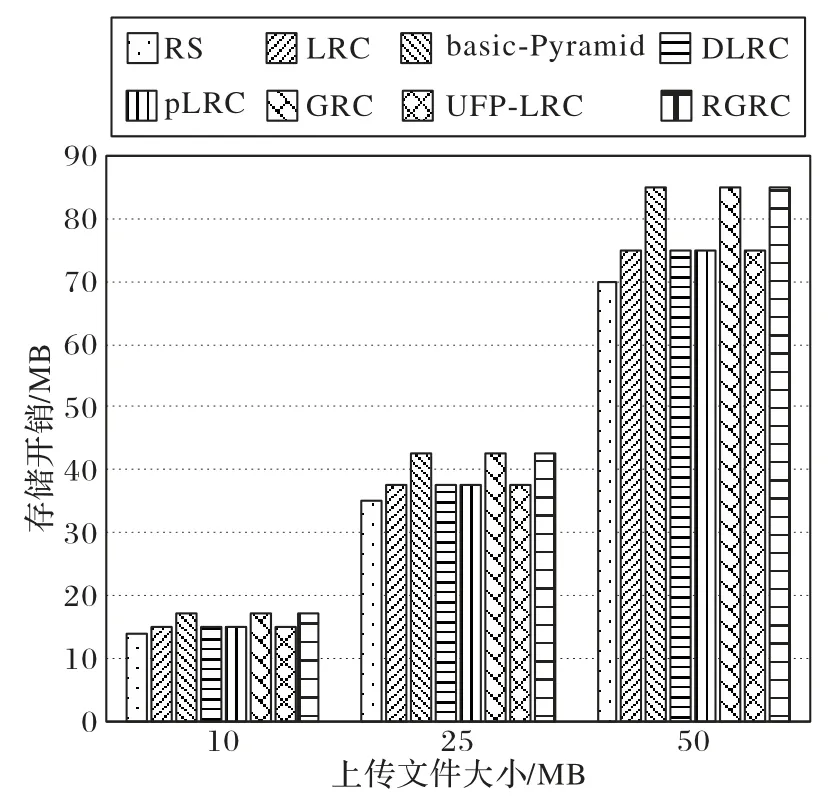
图15 各纠删码的存储开销对比Fig.15 Comparison of storage overhead by different erasure codes

图16 最大容错数和冗余块数的关系Fig.16 Relationship between maximum number of failure tolerance and number of redundant blocks

4 结语

在分布式存储系统中其中大约99.75%故障为单节点失效故障，过高的修复成本将影响分布式存储系统的系统性能，为此，针对现有纠删码中单节点失效修复成本过大、修复时间过长的问题，提出了RGRC。

RGRC 对条带进行分组编码，同时把条带组合成条带集，以条带集为单位编码组内局部冗余块。RGRC 在拥有多容错能力的同时，具备低修复成本和低修复时间的特性，特别针对单节点失效，具有最佳的修复成本和读取成本。实验结果表明，与RS 码相比，RGRC 能降低单节点修复成本约61.8%，修复时间减少约58.7%，仅需增加约21%的存储开销；与LRC、DLRC、pLRC、UFP-LRC 相比，RGRC 能降低单节点修复成本14.8%～57.6%，修复时间减少14.2%～53.2%，仅需增加约13%的存储开销；与basic-Pyamid 码、GRC 相比，RGRC 能降低单节点修复成本约29%，修复时间减少约30%，不需要增加额外的存储开销。同时，RGRC 在多节点失效时也有较高的恢复率和低修复成本性，同时RGRC 灵活性高，能很好地嵌入到分布式存储系统中，具有很好的前景性。