基于EDEM的螺旋式排肥器排肥性能研究

薛 忠,赵 亮,,王凤花,王 槊,宋 刚,王 刚

(1.中国热带农业科学院 农业机械研究所,广东 湛江 524091;2.昆明理工大学 现代农业工程学院,昆明 650500)

0 引言

施肥是热带果园中非常关键的作业环节[1],对水果品质和产量起着至关重要的作用。人工施肥作业难度大,果农劳动强度大和效率低,而机械施肥可以大大减小果农的劳动强度,提高作业效率和降低农业生产成本等。目前,现有的施肥机械排肥方式主要包括离心式、外槽轮式和螺旋式等。胡永光等利用离散元仿真软件EDEM对茶园施肥机离心撒肥过程进行仿真分析和参数优化[2]。祝清震等运用离散元仿真技术研究不同槽轮结构参数对直槽轮式排肥器排肥性能的影响[3]。陈雄飞等设计了一种两级螺旋排肥装置,通过试验测试分析了两级排肥装置的排肥性能[4]。这些研究成果对进一步研究果园施肥机械的排肥性能与优化设计具有关键作用。

目前,市场上广泛使用的排肥器是外槽轮式排肥器,对肥料物理特性有较高要求,但排施干燥颗粒肥时效果良好,排施潮湿颗粒肥及粉状肥时效果较差[4]。螺旋式排肥器对肥料物理特性要求较低,具有可兼施颗粒肥与粉末状肥料、肥量可调等优点,因此以螺旋式排肥器为研究对象,研究肥料颗粒的排肥特性。随着数值模拟技术的飞速进步,离散元法在农业机械研究中得到了广泛运用[1]。杨洲等采用EDEM模拟仿真不同外槽轮排肥器工作参数对其排肥性能的影响,并采用3D打印成型技术加工外槽轮式排肥器进行验证试验[1]。施印炎等运用EDEM软件对稻麦精准变量施肥机排肥过程进行了仿真分析,研究不同排肥器结构对施肥机排肥稳定性的影响,并通过田间试验验证了仿真模型的准确性[5]。苑进等应用离散元法对多种肥料颗粒的撒播和掺混过程进行了数值模拟,对掺混腔结构进行了优化,并分析了其掺混特性[6]。总之,离散元法是一种具有强大优越性和广泛适用性的数值模拟方法,能够很好地展示农业机械的实际工作情况,极大地提高了农业装置研发的工作效率。

本研究以颗粒肥料和螺旋式排肥器为对象,通过三维设计软件SollidWorks对螺旋式排肥器进行建模,采用EDEM建立肥料颗粒的离散元模型,对其排肥过程进行仿真,分析颗粒肥料的运动规律。同时,考察不同工作参数对排肥量的影响显著性,并分析螺旋式排肥器的排肥特性,以期为螺旋式排肥器进一步研究提供参考依据。

1 排肥器结构及参数设定

1.1 结构设计

螺旋式排肥器主要由5个部分构成,即肥箱、螺旋叶片、排肥轴、排肥盒和排肥口[7],如图1所示。其中,肥箱尺寸为280mm×260mm×270mm,排肥轴直径设定为25mm。综合考虑果园所需施肥量及肥料物理特性等,并通过公式计算取螺旋叶片直径为80～100mm,螺距为50～70mm。

图1 螺旋式排肥器模型

1.2 主要参数确定

1.2.1 排肥量

排肥量是螺旋式排肥器排肥能力的一个关键指标,可根据实际需求量排施,与排肥器结构参数有关。在排施肥料时,排肥轴所占截面积对排肥器排肥能力有一定影响,而相对于整个施肥机来说,其轴径很小,往往忽略其轴向阻滞的作用。因此,螺旋式排肥器的排肥量可近似按下式计算,即

Q=47D2·n·S·λ·ε·φ

(1)

式中Q—排肥量(t/h);

D一螺旋叶片直径(mm);

n一排肥轴转速(r/min);

S一螺距(mm);

λ一颗粒肥料的密度(t/m3);

ε一倾斜输送系数;

φ—填充系数。

从公式(1)可以看出:螺旋式排肥器的排肥量Q与排肥器参数D、n、S、λ、ε和φ有关。当排肥量Q确定后,可以适当调整螺旋叶片直径D、排肥轴转速n、螺距S和填充系数φ等,以满足排肥量Q的需求。

施肥机在连续施肥向前行走1个株距时,螺旋式排肥器的排肥量为

(2)

式中v一施肥机的前进速度,取v=1.98km/h;

g—每株施肥量,取g=0.3～0.5kg/株;

s—果树平均株距长度,取s=1.82m。

把各数据代入公式(2)中,计算得

(3)

1.2.2 螺旋叶片直径与螺距

螺旋叶片直径是螺旋式排肥器的一个重要参数,其设定将会直接影响排肥量,通常根据排肥装置的结构形式、肥料物理特性和排肥能力大小等来确定螺旋叶片直径。

根据公式(4)可确定螺旋叶片直径为

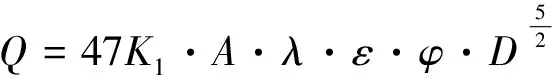
(4)

(5)

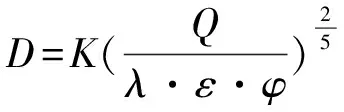
(6)

式中Q—排肥量(t/h);

D—螺旋叶片直径(mm);

K1—螺旋叶片直径与螺距的比例系数,当水平布置时,K1=0.8～1.0;当倾斜布置或肥料流动性较差时,K1≤0.8,参考表3取K1=0.5;

A—肥料综合特性系数(见表2),取A=28;

λ—肥料的容积密度,经测量λ=0.938t/m3;

ε—倾斜输送系数(见表 1),本文设计的螺旋式排肥器为水平安装,参考表1,取ε=1;

φ—填充系数,参考表2取φ=0.3。

通过计算,得出D=80～98mm。由于螺旋叶片直径通常设计成标准系列,如D=100、150、200、250、300mm等,故螺旋叶片直径D选用范围为80～100mm。

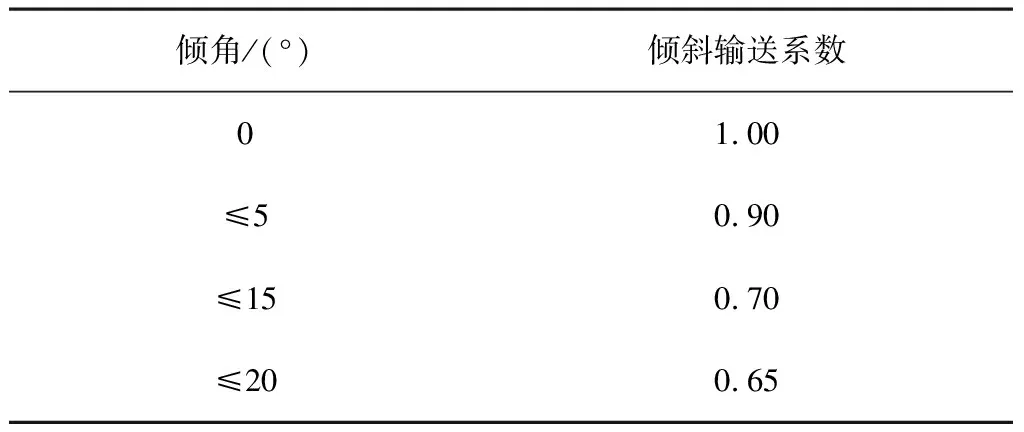
表1 倾斜输送系数表

表2 物料综合特性

螺距一方面决定着螺旋升角大小,另一方面螺距的改变会使颗粒运动速度分布发生变化,所以螺距对排肥器排肥能力的影响较大。

通常根据经验公式来计算螺距,即

S=K1·D

(7)

其中,K1为螺距与螺旋叶片直径的比例系数。对于水平布置的排肥器,K1通常取0.5～0.9,故螺距S取50～70mm。

1.2.3 转速

排肥轴转速对排肥量有较大的影响:加快排肥轴转速,排肥器的排肥量提高;减小转速,排肥量下降。但排肥轴转速不能过大,因为当转速超过一定临界值时,肥料会产生过大离心力而向外抛导致无法正常排肥,所以需要对转速进行一定的限制, 不能大于某一临界值。通常排肥轴转速由排肥量、肥料物理特性和螺旋叶片直径等确定。

当螺旋外侧的颗粒肥料不产生径向运动时,它所受离心力的最大值与自身重力之间的关系为

(8)

(9)

考虑到受不同物理特性肥料的影响,可得

(10)

(11)

(12)

式中m—肥料质量(kg);

ωmax—排肥轴临界角速度(rad/s);

r—螺旋半径(m);

nmax—排肥轴临界转速(r/min);

g—重力加速度(m/s2);

D—螺旋叶片直径(m);

K—肥料综合系数;

A—肥料综合特性系数。

通过计算可得最大排肥轴转速为89r/min。根据排肥量、肥料物理特性和螺旋叶片直径等来确定排肥轴转速,在满足排肥量要求情况下排肥轴转速不宜过高, 更不允许超过它的临界值, 即

n≤nmax

(13)

式中n—排肥轴实际转速(r/min)。

2 肥料颗粒离散元模型建立与参数确定

2.1 肥料颗粒离散元模型

肥料颗粒的形状和密度将直接影响其在排肥盒中的运动情况以及排肥量。为了使肥料颗粒排肥过程更贴近实际,以常用的尿素颗粒为研究对象,随机选取100个颗粒,测量其三维尺寸和密度等,计算公式为

(14)

(15)

式中D—等效直径(mm);

L—长度(mm);

W—宽度(mm);

T—厚度(mm);

Φ—球形率。

经计算,颗粒参数如表3所示。

表3 肥料颗粒参数

由表3可知:尿素颗粒的球形率为86.3%,形状近似椭球体,平均长度为4.031mm,平均宽度为3.305mm,平均厚度为3.152mm。采用EDEM建立尿素颗粒的离散元模型,设置长轴为4.0mm,短轴为3.3mm。由于EDEM软件无法直接建立椭球体,故本文采用5个球体填充方式建立颗粒离散元模型,5个球体半径设置为1.55、1.6、1.65、1.6、1.55mm。尿素颗粒离散元模型如图2所示。

图2 肥料颗粒离散元模型

2.2 仿真参数确定

采用EDEM软件默认的无滑动接触模型(Hertz-Mindlin(no-slip))进行肥料颗粒的仿真分析,能得到十分准确而高效的仿真结果。在三维设计软件SolidWorks中建立螺旋式排肥器的实体模型,并以igs格式导入EDEM求解环境中,同时设置螺旋式排肥器的所有部件材料为碳素结构钢Q235。

在EDEM前处理模块中,排肥器和肥料颗粒的参数设定对仿真速度有较大影响。通过测量可得尿素颗粒密度为1 377kg/m3,另采用高速摄像机和摩擦测试仪等设备测得其碰撞恢复系数、静摩擦因数和滚动摩擦因数,其余仿真参数参考《农业机械设计手册》和孙雪松等学者的研究成果[8-10]。其相关物理力学参数如表4所示。

表4 物理力学参数

3 仿真试验与分析

3.1 试验设计

在仿真试验之前,设置计算时间步长为瑞利时间步长的20%,仿真时间为5s。颗粒工厂中,肥料颗粒生成方式设置为动态生成,生成总质量为8kg,将肥料颗粒设置为正态分布,可使肥料颗粒与实际肥料颗粒尺寸分布更加接近,仿真网格为2倍的颗粒半径;仿真结束后,可通过EDEM后处理模块获得肥料颗粒的运动轨迹、速度及受力变化曲线图等。仿真排肥过程如图3所示。

图3 仿真试验过程

由螺旋式排肥器工作原理可知:其主要结构参数和工作参数为螺旋叶片直径、螺距、入肥口大小、排肥口大小和排肥轴转速等。因此,以螺旋叶片直径x1、螺距x2和排肥轴转速x3为试验因素,以排肥量y为试验指标,对其进行排肥性能研究,仿真试验因素及水平如表5所示。

表5 仿真试验因素水平

排肥量y计算公式为

(16)

其中,y为排肥量(g/s);m1为t1时刻排肥量检测区内肥料颗粒的质量(g);m2为t2时刻排肥量检测区内肥料颗粒的质量(g)。

3.2 仿真分析

3.2.1 单圈排肥量与转速的关系

排肥器的单圈排肥量是衡量其排肥性能的一个重要指标,在排肥轴不同转速的情况下,其单圈排肥量的稳定性与均匀性直接影响到排肥器排肥的稳定性与均匀性[4]。在转速一定的情况下,若已知排肥器每分钟排肥量,则排肥器的单圈排肥量计算公式为

q=Q/n

(17)

其中,q为单圈排肥量(g);Q为排肥量(g/min);n为排肥轴转速(r/min)。

当螺旋叶片直径为90mm、螺距为60mm时,考察转速与单圈排肥量之间的关系。由式(17)可以计算出单圈排肥量,结果如表6所示。

表6 单圈排肥量与转速的关系

续表6

由表6可知:对于不同转速下的排肥器单圈排肥量变异系数均小于2%。这表明,本文建立的螺旋式排肥器模型结构合理,排肥稳定性与均匀性较好。

3.2.2 肥料颗粒运动过程仿真

当螺旋叶片直径为90mm、螺距60mm、排肥轴转速为35r/min时,对肥料颗粒的运动过程进行仿真。仿真运行后,肥料颗粒由颗粒工厂开始掉落。0～0.5s内,颗粒持续掉落,最终全部掉落至肥料箱和排肥盒中。将出口处肥料颗粒的速度和受力着不同种颜色,其中浅色代表速度和受力值最大,深色代表速度和受力值最小。这样能更直观地观察肥料颗粒的运动轨迹、速度及受力变化情况,如图4～图5所示。

图4 肥料颗粒速度分布

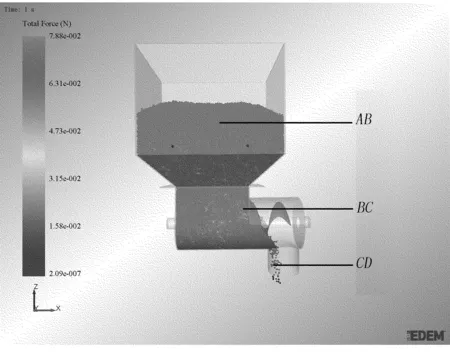
图5 肥料颗粒受力分布

将图4、图5中颗粒运动速度和受力进行分区,可分为如下几个区域:AB区域,肥料颗粒掉入料箱中,速度先增大后减小,受力值波动较大;BC区域,肥料颗粒在重力作用下继续下落并掉入排肥螺旋内,并在排肥螺旋作用下继续运动,此时颗粒与颗粒之间相互碰撞和挤压,其速度无明显变化,受力值继续产生波动;CD区域,肥料颗粒在排肥螺旋转动作用下逐渐脱离肥料群,进入CD区域,由于自身重力和离心力的作用,速度有小幅上升达到1.279m/s,碰到地面后下降为0,受力值无明显波动并趋于平稳,最后完成肥料颗粒的排出。

EDEM软件中,会对生成的颗粒进行自动编号,方便研究人员对单个肥料颗粒运动状态进行研究。为了更好地研究螺旋式排肥器排肥性能,随机选取肥料箱左、中和右侧的单个肥料颗粒,编号分别为237号、1255号和54687号;仿真计算结束后,可以在EDEM软件后处理模块中获得不同位置的单个肥料颗粒运动轨迹、速度及受力值变化曲线图,从而进一步分析颗粒在排肥过程中的运动规律,如图6～图8所示。

图6 单个肥料颗粒运动轨迹图

图7 单个肥料颗粒速度随时间变化曲线图

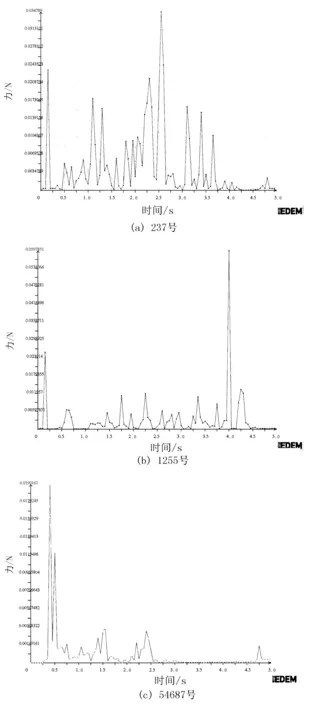
图8 单个肥料颗粒受力随时间变化曲线图

由图6可以看出:237号、1255号和54687号肥料颗粒的运动轨迹图各不相同,但三者最后皆可由排肥口顺利排出,未出现拥堵、架空和断条现象。

由图7(a)和图8(a)可知:0s时,237号肥料颗粒由颗粒工厂生成并开始下落,落至AB区域;0～0.4s内,237号肥料颗粒的速度和受力值皆为先增大后减小,0.05s时速度达到最大值为2.478m/s,在0.4s时该肥料颗粒速度减小为0.022m/s。通过观察仿真动画可知:0.4秒时,颗粒掉落了肥箱内并停在肥料群上;0.4～4.5s内,237号肥料颗粒速度变化不大,变化范围在0.018～0.07m/s之间,受力值产生了较大波动,2.55s时达到了最大值为0.035N。通过观察仿真动画可知:该肥料颗粒继续下落并掉入排肥螺旋内,接着开始随着排肥螺旋进行旋转运动,由于颗粒之间无明显运动,所以其速度变化很小,在其他颗粒挤压和螺旋转动作用下,该肥料颗粒受力波动较大,此时其位于BC区域;4.5～5s内,237号肥料颗粒随着螺旋转动,并在自身重力和离心力作用下逐渐脱离肥料群进入CD区域,颗粒速度出现小幅上升达到1.472m/s,碰到地面后下降为0,受力值趋于平稳;在4.8s时,237号肥料颗粒速度突然小幅下降且受力值小幅上升,此时该肥料颗粒碰撞上了排肥口,故速度和受力出现变化,随后其漂离仿真区域,完成肥料颗粒的排出。

由图7(b)和图8(b)可观察出:1255号和237号肥料颗粒有类似的速度变化规律,受力变化规律不相同。0s时,1255号肥料颗粒由颗粒工厂生成并开始下落,落至AB区域;0～0.2s内,1255号肥料颗粒的速度和受力值皆为先增大后减小,0.1秒时速度达到最大值为2.913m/s;在0.2s时,该肥料颗粒速度减小为0.03m/s,通过观察仿真动画可知:0.2s时,颗粒掉落了肥箱内并停在肥料群上;0.2～4.6s内,1255号肥料颗粒产生了较小的速度变化,变化范围在0.021～0.061m/s之间,受力值产生了不规律的波动,4s时其达到了最大值为0.06N。通过观察仿真动画可知:该肥料颗粒继续下落并掉入排肥螺旋内,接着开始随排肥螺旋进行旋转运动,由于颗粒之间无明显运动,所以其速度变化很小。4s时,该肥料颗粒与螺旋和肥料群发生碰撞,使其受力产生较大波动并达到最大值,此时其位于BC区域;4.6～5s内,1255号肥料颗粒随着螺旋转动,并在自身重力和离心力作用下逐渐脱离肥料群,颗粒速度出现小幅上升达到1.266m/s,受力值趋于平稳,碰到地面前后下降为0,随后其漂离仿真区域,完成肥料颗粒的排出。

由图7(c)和图8(c)可以看出:54687号和237号肥料颗粒有类似的速度变化规律,受力变化规律不相同。0.25s时,54687号肥料颗粒由颗粒工厂生成并开始下落,落至AB区域;0.25～0.5s内,54687号肥料颗粒的速度和受力值皆为先增大后减小,0.35s时速度达到最大值为2.496m/s,0.4s时受力值达到最大值为0.02N。其主要是因为该肥料颗粒与其他颗粒发生摩擦和碰撞,从而使其速度和受力值波动较大,0.5s时该肥料颗粒速度减小为0.022m/s。通过观察仿真动画可知:0.5s时,颗粒掉落了肥箱内并停在肥料群上;0.5～2.9s内,54687号肥料颗粒速度变化不大,变化范围在0.002～0.022m/s之间,受力值产生了不规律的波动,该肥料颗粒与肥料群发生碰撞,但仍停留在BC区域,未出现明显前进运动;2.9～4.5s内,54687号肥料颗粒速度出现增长趋势,产生了较小的速度变化,变化范围在0.016～0.081m/s之间,受力值趋于平稳,此时处于BC区域。通过观察仿真动画可知:2.9s时,54687号肥料颗粒开始随着排肥螺旋进行旋转运动,在排肥螺旋转动作用下,其速度出现增长趋势,由于颗粒之间无明显运动,所以其运动速度变化很小且受力值趋于平稳;4.5～5s内,54687号肥料颗粒随着螺旋转动,并在自身重力和离心力的作用下逐渐脱离肥料群进入CD区域,颗粒速度出现小幅上升达到1.422m/s,受力值趋于平稳,碰到地面后下降为0,随后其漂离仿真区域,完成肥料颗粒的排出。

综上所述,在螺旋式排肥器排肥过程中,分别选取肥料箱左、中和右侧的单个肥料颗粒,对其运动过程进行仿真,不同位置的单个肥料颗粒运动轨迹各不相同,但三者最后皆可由排肥口顺利排出,未出现拥堵、架空和断条现象。不同位置的单个肥料颗粒速度变化规律基本相同,皆为0～0.5s内颗粒肥料速度波动较大,0.5-4.5秒内产生了较小的速度变化,4.5～5s内速度出现小幅上升,在碰到地面前速度达到一定值,之后急速下降为0;不同位置的单个肥料颗粒受力变化规律各不相同,这是因为每个肥料颗粒运动过程复杂,随着排肥螺旋的转动,其在排肥盒、排肥螺旋和肥料群的作用下受力值会产生不规律的波动。

3.2.3 不同工作参数仿真分析

当螺距为60mm、排肥轴转速为35r/min时,排肥量随螺旋叶片直径变化,仿真试验结果如表7所示。对回归数学模型及系数进行显著性检验可知:螺旋叶片直径对排肥量影响显著(P<0.05)。将螺旋叶片直径与排肥量进行线性拟合,可得两者的回归曲线,如图9所示。回归数学模型拟合度R2=0.907,表明曲线拟合好。螺旋叶片直径与排肥量呈线性负相关关系,其关系式为

y=183.162-0.641x1

(18)

式中y—排肥量(g/s);

x1—螺旋叶片直径(mm)。

表7 不同螺旋叶片直径仿真结果

图9 螺旋叶片直径与排肥量的回归曲线

当螺旋叶片直径为90mm、排肥轴转速为35r/min时,排肥量随螺距变化,仿真试验结果如表8所示。对回归数学模型及系数进行显著性检验可知,螺距对排肥量影响极显著(P<0.01)。将螺距与排肥量进行线性拟合,可得两者的回归曲线,如图10所示,回归数学模型拟合度R2=0.955,表明曲线拟合好。螺距与排肥量呈线性正相关关系,其关系式为

y=2.926x2-46.164

(19)

式中y—排肥量(g/s);

x2—螺距(mm)。

表8 不同螺距仿真结果

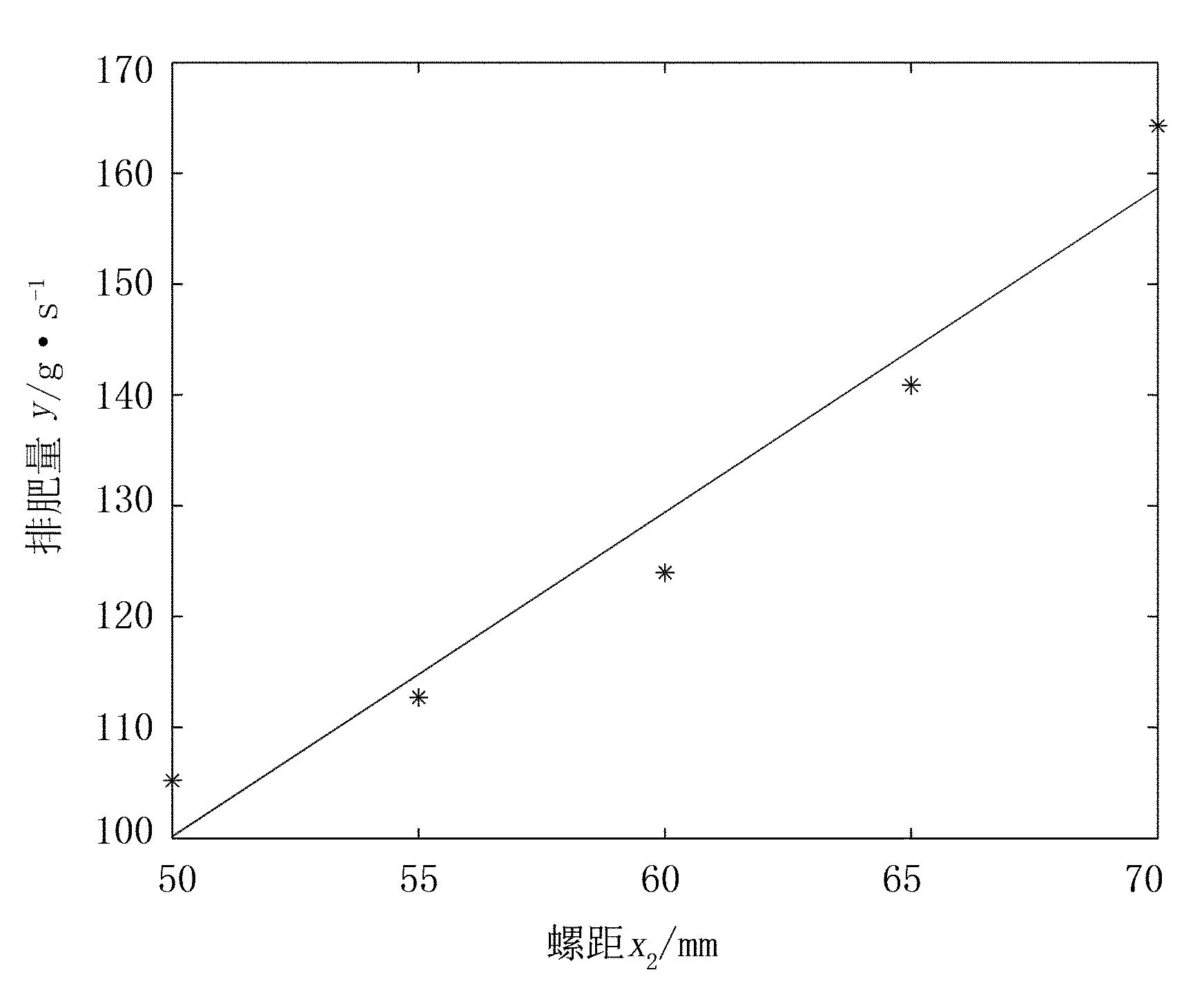
图10 螺距与排肥量的回归曲线

当螺旋叶片直径为90mm、螺距为60时,排肥量随排肥轴转速变化,仿真试验结果如表9所示。对回归数学模型及系数进行显著性检验可知,排肥轴转速对排肥量影响极显著(P<0.01)。将排肥轴转速与排肥量进行线性拟合,可得两者的回归曲线,如图11所示。回归数学模型拟合度R2=0.987,表明曲线拟合好。排肥轴转速与排肥量呈线性正相关关系,其关系式为

y=4.261x3-18.28

(20)

式中y—排肥量(g/s);

x3—排肥轴转速(r/min)。

表9 不同排肥轴转速仿真结果

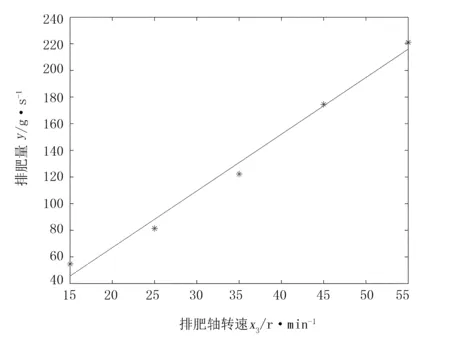
图11 排肥轴转速与排肥量的回归曲线

4 结论

1)不同转速下的排肥螺旋单圈排肥量变异系数均小于2%,表明本文所建立的螺旋式排肥器模型结构合理,排肥稳定性与均匀性较好。

2)肥料箱左、中和右侧的单个肥料颗粒运动轨迹各不相同,速度变化规律基本一致,受力变化规律各不相同。这是因为每个肥料颗粒运动过程复杂,随着排肥螺旋的转动,其在排肥盒、排肥螺旋和肥料群的作用下受力值会产生不规律的波动。

3)仿真分析不同工作参数与排肥量的关系可知:螺旋叶片直径对排肥量影响显著(P<0.05),满足线性负相关;螺距和排肥轴转速对排肥量影响极显著(P<0.01),满足线性正相关。本文研究结果为螺旋式排肥器进一步优化设计提供了基础数据。