考虑车位异质性的共享停车平台最优分配机制研究①

张利凤，慕银平，樊鹏英

（1.电子科技大学 经济与管理学院，成都 611731；2.北京工商大学 经济学院，北京 100048）

截至2015 年底，北京机动车保有量达560 余万辆，机动车停车位约290 万个，基本车位缺口达350 万个［1］。停车难成为困扰车主出行的一大难题。为了缓解停车难问题，在物联网、互联网等技术的支持下，可将由于出差、上班等原因长期处于闲置的私家车位停车时段共享出来，供其他需求者使用。车位共享平台应运而生，如ECTP（engelhart commodities trading partners）、ywpark、pnpark 等。通过这些共享平台，车位拥有者可以发布车位空闲时段信息，车位需求者可以通过平台寻找合适的停车位置和时段。因此，共享平台使稀有的车位资源得到了有效的利用，不仅可以缓解停车难问题，还可以增加私家车位拥有者的收入。在平台的运营过程中，由于车位拥有者所发布的车位空闲时段及位置信息与车位需求者发布的需求时段及位置需要进行高效的匹配，因而产生了大量的科学问题需要解决，如车位分配、车位定价等问题。

一、文献综述

关于车位管理有大量的研究问题，其中大多数研究集中在车位的动态定价和分配方面。Shiftan 和Golani［2］研究发现通过调整定价策略，可以影响出行方式从而减少停车需求，以缓解停车难问题；Qian 和Rajagopal［3］运用动态规划模型求解停车位随机定价问题，给出车位占有率的阈值，当车位占用率超过该阈值则应该进行收费；Nourinejad 和Roorda［4］提出了按道路收费和按小时收费两种机制，并得出按道路收费将严格地减少需求，但是按小时收费则可以根据停留时间弹性减少或诱导需求。除此之外，还有很多学者对停车位定价进行了相关研究［59］。虽然大量研究表明，通过定价策略可以在一定程度上缓解停车难问题，但是随着汽车保有量的快速增加，定价策略对缓解停车难的作用逐渐减弱。智能停车系统的出现为优化停车位分配提供了技术支持。通过智能停车系统，需求者可提前预约车位，停车场经营者可以根据预约信息进行车位优化分配。Teodorovic 和Lucic［10］构建整数规划模型研究了多个价格等级下，停车位可预约的收益管理问题；Geng 和Cassandras［11］构建混合整数规划模型研究了智能预约系统下的停车位分配策略；Boudali 和Ouada［12］提出了一种基于多智能体的智能停车系统，通过处理驾驶员的偏好，进行车位分配，为驾驶员提供实时决策辅助；Lei 和Ouang［13］提出运用拉格朗日松弛设计近似算法对智能停车的动态定价和预约分配问题进行求解；Martha 等［14］以收益最大化为目标构建了多个停车场下的车位分配问题，并通过人工神经网络进行实时在线预订决策。上述学者的研究大多针对传统的停车场车位定价或者分配进行研究。考虑到传统的停车场的停车位数量固定，且每个车位可供停车时长也是固定的，因此实际上该类问题属于供给确定，需求随机下的能力优化分配。由于车位共享平台的车位是由私家车位拥有者提供，而私家车位拥有者的车位空闲时间不同，导致车位可供停车的时长具有随机性。同时每个时间段提供的车位数量也依赖于私家车位的空闲时间，因此每个时间段共享平台的车位数量也具有随机性。即车位共享平台所提供的停车位数量随机，且每个车位可供停车的时长也是随机的，因此车位共享平台所面临的车位分配比传统停车场的车位分配决策更为复杂。传统的车位分配模型将不再适用于共享平台的车位分配，车位共享平台面临的将是随机的供给和需求下的车位分配决策问题。

随着互联网技术的发展，共享经济出现，提高了闲置资源的利用率，各领域也出现了大量的共享平台［15］。关于车位共享问题的研究，李涛和关宏志［16］研究了车位外部使用者和内部使用者时间相冲突的情况下，通过需求调节共享终止时刻、停车位供应率等设计停车共享优化方案以实现停车管理者的收益最大化；Guo 等［17］构建高斯混合模型刻画了停车位管理者向车位拥有者回购车位并出租给需求者的情况下，实现利润最大化的随机优化问题，并通过仿真得到最优回购量；Zou 等［18］以最大化社会福利为目标函数，构建整数规划模型分别研究了静态和动态的车位分配机制；Shao 等［19］运用0 1 规划模型研究了当车位共享信息与需求信息已知的情况下的车位分配问题；Su 等［20］设计了两种机制研究私家车位既可以交换也可以出租两种情况下的车位分配问题，得到所提出的机制可以显著提高社会福利；林小围等［21］构建整数规划模型，研究了带不同时间窗口的共享平台下私家车位的动态预约与分配策略。虽然上述文献对车位共享平台下的车位分配问题进行了研究，但是目前对共享车位的研究均假设停车位对于车位需求者具有同等效用，即平台用任意一个车位去满足顾客需求所获得的收益均相同。由于车位的供给者为私家车位拥有者，因此共享平台提供的停车位位置可能会出现差异性较大的问题。当停车位位置差异性较大时，用不同的车位位置去满足顾客，将会影响顾客停车后的行走距离。云美萍等［22］的研究表明步行距离是停车者优先考虑的因素之一。此时，对于顾客而言，用不同的车位去满足顾客的需求将产生不同的效用，从而影响平台的收益，所以车位分配决策应该考虑车位的异质性。

综上，本文以车位共享为背景，研究了随机供给和需求的情况下，车位共享平台在考虑车位异质性情况时的车位分配机制，为共享平台的预订分配提供决策支持。

二、问题描述

在实际中，顾客到达目的地的步行距离（简称“步行距离”）是影响顾客满意度的重要因素，步行距离越远，顾客的满意度越低，反之，则越高。当两个车位的距离较近，顾客的步行距离差异较小时，可以认为两个车位不具有异质性；当两个车位距离较远，步行距离的差异较大时，可以认为两个车位具有异质性。基于此，本文利用顾客的步行距离对车位的异质性进行刻画。进一步，平台可根据车位之间的距离将停车位划分为不同的区域。同一个区域车位间的距离较近，不具有异质性，而不同区域车位间的距离较远，则具有异质性（实际中的划分标准：以同一个小区作为一个区域或以一定的公里范围作为一个区域）。因此，不同区域车位的差异可用步行距离来刻画。当车位供给（需求）用户在平台上发布停车位信息时，需包含以下信息：车位的供给（需求）时间段，车位的供给（需求）位置区域。本文所考虑的车位属于稀缺资源，当顾客需求停车区域的车位不足时，平台可能会用其他区域的车位去满足需求。此时，顾客停车后的步行距离会增加，导致顾客满意度下降，从而会为平台带来损失，因此平台需要根据不同用户提供的车位信息对车位进行优化分配。

由于车位供给者可能提供的时间段有限，因此将决策周期离散化为T个周期。假设供给者最多可以提供T个周期的停车时段，需求者也最多可以连续停留T个周期。由于出行时间的随机性，车位供给者和车位需求者可能随时将供给信息和需求信息提供给平台，因此共享平台应该根据时变的供给信息和需求信息，更新决策，动态地分配停车位。

（一）停车位的动态模型构建

假设平台存在J个具有异质性的区域，每个区域有Nj（j=1，2，…，J）个停车位。因此共有车位。不同区域之间的距离为D=（dij）J×J，其中dij表示第i个区域到第j个区域的距离，假设dij=dji。由于涉及多个异质区域，因此车位位置的划分状态用变量C=（cnj）N×J表示，其中：

考虑到每个周期都可能有车位供给者和车位需求者将车位信息提供到平台上，因此τ周期新增的车位供给信息应包含车位的可用时间段、车位的位置状态等。τ周期新增的车位可用时间段用变量表示，其中：

如若Aτ中第n行=（1，1，0，…，0），则表示τ周期第n个车位新增第1、2 个周期可以用于停车。假设τ周期新增的停车位需求有Mτ个，由于停车位的需求信息包含顾客预约的停车时间及车位位置，因此顾客的预约时间用变量来表示：

为了更能够反映现实情况，分配车位时不考虑在中途挪动车辆到另一个停车位，即不允许用多个供给满足一个需求。定义τ周期的分配决策变量为；m=1，2，…，Mτ；n=1，2，…，N。其中=1 表示τ周期新增的第m个需求被分配到第n个停车位，=0 表示τ周期新增的第m个需求未分配到第n个停车位。根据决策变量可以给出τ周期停车位的使用情况记为

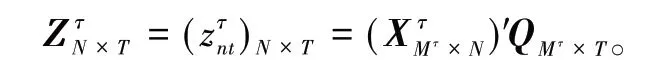
假设平台每成功出租一个车位，单位时间固定支付p0给车位供给者。平台每成功出租一个车位平台所获得的单位收益为p，则τ周期平台的总利润为。用表示顾客分配到各区域的状态，其中。若=1，表示τ周期第m个需求被分配到第j个区域；若=0，表示τ周期第m个需求未被分配到第j个区域。因此车位位置的需求与供给匹配矩阵为，其 中=1 表示τ周期顾客预约的是第j个区域被实际分配到第i个区域；=0 表示顾客预约的是第j个区域未被实际分配到第i个区域。由于车位的稀缺性，可能会出现顾客预订区域车位已经停满的情况，此时，平台可能会用其他区域的车位去满足顾客的预订需求。不同区域的车位具有异质性，分配其他区域的车位给顾客会改变步行距离，从而影响顾客的满意度。步行距离越远，顾客的满意度越低，平台面临的惩罚成本越高，因此，车位异质性对平台决策的影响可用步行距离带来的惩罚成本进行量化。若每增加一单位步行距离为平台带来的惩罚成本为π，则τ周期分配第i个区域的车位给需求为第j个区域的顾客所带来的惩罚成本为。不同区域的车位所带来的惩罚成本不同，因此不同区域车位的异质性差异程度可由量化。由于τ周期顾客总的行走距离，因此平台在分配中因车位异质性带来的总的惩罚成本为。综上可得，τ周期平台获得的总利润由车位出租的利润和车位异质性带来的惩罚成本构成，具体表达式如式（1）所示：

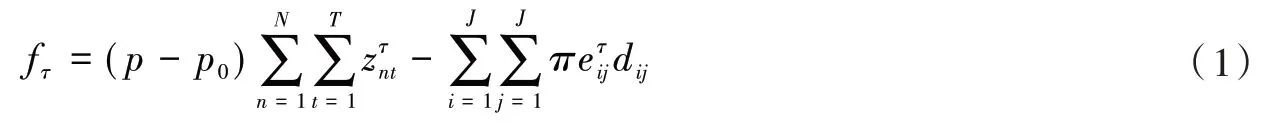
记τ周期剩余的车位为表示τ周期第n个车位在第t个周期有效；=0 时表示τ周期第n个车位在第t个周期不可使用。在τ周期剩余车位为Iτ，新增车位信息为Aτ、Qτ、Lτ的前提下，τ周期到T周期的总利润记为Gτ（Iτ|Aτ，Qτ，Lτ），则随机动态车位分配模型（random dynamic parking space allocation model，RDP）为

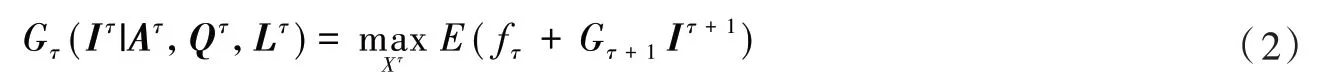
当在τ周期进行决策后，剩余的车位Iτ+1=Iτ+Aτ-Zτ，其中。因此，RDP模型在τ周期进行决策时应该满足的可行停车位分配策略集为

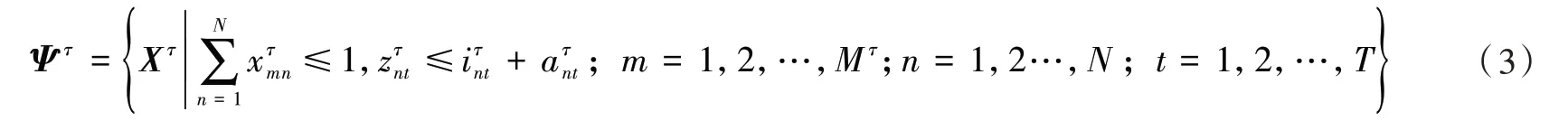
定理1：当时，=0。

证明：根据，显然对于平台而言，其分配一个车位的目的是希望获得收益。当τ周期面临的需求信息和供给信息分别为Iτ、Aτ、Qτ、Lτ时，将决策变量Xτ展开为向量。τ周期将第m个需求分配到第n个车位所获得的利润为，而当平台将第m个需求分配到第n个车位所带来的惩罚成本为。当=1，则平台得到的利润为。显然若，平台得到的利润为负，此时平台不会将τ周期的第m个需求分配到第n个车位。所以有时，则平台不愿意将第m个需求分配到第n个车位，即=0。

定理1 给出了车位分配的基本原则，即当惩罚成本和单位租赁利润满足定理1 所给的条件时，平台不会将第m个需求分配到第n个车位。

性质1：若用表示第m个顾客的需求向量，有且=1，则=0，j≠i。其中1T×1=（1，1，…，1）′。

证明：因假设不允许部分满足顾客的需求，所以若满足顾客的需求，则对于平台而言，租赁车位的总时间为，因此其总收益为。顾客希望停在第i个区域而被分配到第j个区域则面临的惩罚成本为πdij。当满足顾客m的需求获得的利润时，平台将不愿意采用该分配方案去满足顾客。

性质1 给出了区域分配的基本原则。通过性质1 可以得到，平台在用其他区域的车位去满足顾客的需求（跨区域分配）时，需要权衡租赁车位带来的惩罚成本与单位租赁利润之间的关系。定理1 和性质1 在进行模型求解时，可以排除掉一部分可行解，即将约束条件0 ≤≤1 中满足定理1 和性质1 的决策变量范围改为0，从而简化求解过程。

尽管定理1 和性质1 可以在一定程度上简化求解过程，但是并未实现决策变量或者状态变量的降维，因此并未从本质上解决RDP模型的计算复杂度。由于供给和需求信息在每个周期具有随机性，因此在τ周期进行决策时，其可能出现的状态有以下结论：

性质2：若At、Qt、Lt的状态相互独立且分别有Ut、Vt、Wt个，则τ周期进行最优决策时，τ+1 到T周期RDP模型可能出现的状态变量（车位可用时间状态）最多可达到种，其中；t=τ+2，…，T；特别的，=1。

证明：由于At、Qt、Lt均为矩阵，其维度较高。在RDP模型进行决策时，需要考虑后续周期可能出现的状态。若假设每个周期At、Qt、Lt的状态分别有Ut、Vt、Wt个，则当τ周期进行最优决策时，需考虑τ+1 到T周期的期望利润。当τ周期进行决策后，τ+1 周期的车位状态为Iτ+1。考虑到τ+1 周期出现的Aτ+1、Qτ+1、Lτ+1将会影响τ+2 周期的状态变量，若假设t周期的状态变量个数为，则τ+2 周期Iτ+2可能出现的状态为个，τ+3 周期Iτ+3可能出现的状态个数为。以此类推，t+1 周期的状态变量个数为。特别的若每个周期可能出现的状态个数相等，则状态变量呈指数增长。

由于需求和供给为连续周期，在τ+1周期时，任意一个车位的供给时间的状态有种可能。假设有N个车位，不同车位可用时间状态为独立状态。考虑车位数量和决策周期的限制，则状态变量在τ周期进行决策后，最多可能出现种状态。综上，RDP模型进行决策时，后续周期状态变量的可能状态数量将急剧增加，最多可能出现种状态。

根据性质2，可得即使只有5 个停车位，共划分为5 个周期。若当前决策周期τ=2 且每个周期的Ut、Vt、Wt均相等，Ut=Vt=Wt=2，则后续周期可能会出现的状态变量为16807 种，因此式（2）的计算复杂度非常高，无法直接进行求解。为能够在有效时间内解决该问题，接下来将设计近似算法以给出近似分配策略。

（二）单周期分配策略

由于模型RDP的计算复杂度很高，其车位分配决策难度大，无法在有效时间进行求解。又因为车位的价值较低，所以平台在做决策时，更强调决策的高效性。为实现决策的高效性，平台在实际决策中通常以某一个时段，如一天或者一个小时，进行收益最大化决策。此时平台不会考虑将现有车位预留到后期，以获得更高的收益。即进行决策时，平台仅考虑当前周期目标函数最大化。由于τ周期进行决策时是基于Aτ、Qτ、Lτ已知的前提下进行车位的分配，因此以单周期的收益最大化为目标函数的停车位分配模型（parking space allocation model，PSA）可构建如下：

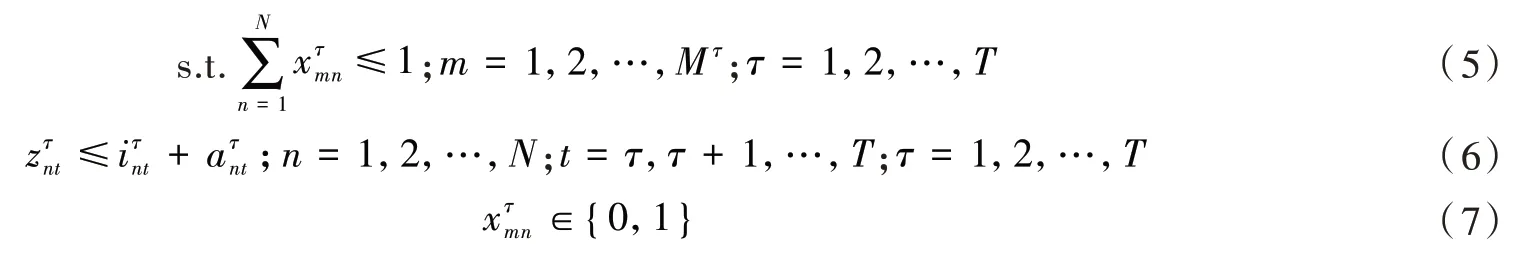
约束条件（5）说明一位顾客只能分配到一个车位；约束条件（6）说明车位分配的时间不能超过车位的供给时间，当进入τ周期决策时，应该是对τ到T周期的车位时间有效时间进行分配，所以t≥τ；约束条件（7）表示顾客是否分配到车位的状态。由于PSA模型考虑单周期收益最大化，因此在每个周期进行决策后，当前周期的剩余车位将留到下一个周期，且满足Iτ+1=Iτ+Aτ-Zτ。τ周期的优化模型记为PSAτ，可将PSAτ模型改写为矩阵的形式。PSAτ模型的决策变量为，因为，所以决策变量关于的系数向量为

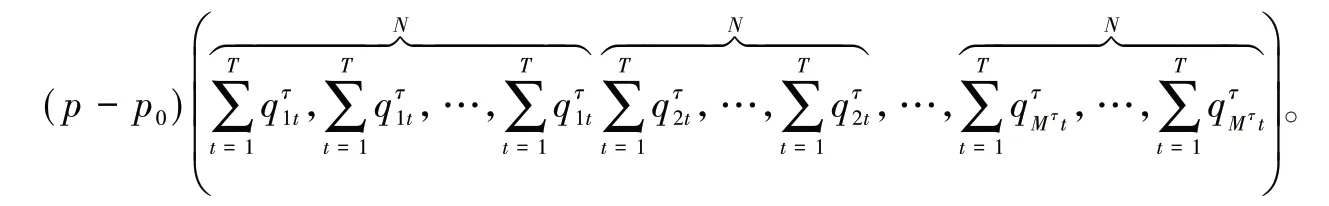
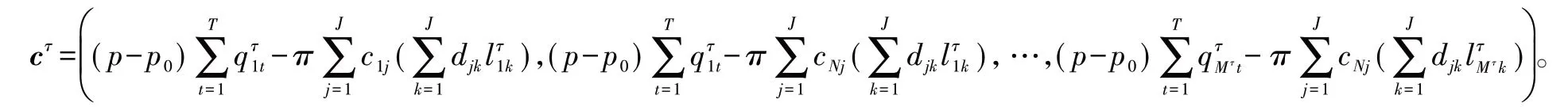
将PSAτ模型中约束条件构造为不等式约束矩阵，具体形式如下：

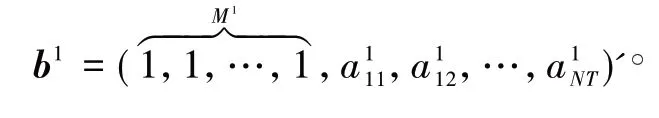
因此PSAτ模型的矩阵形式为

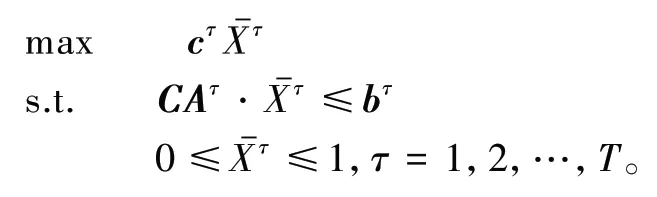
具体的算法步骤如下：

Step1：初始化决策周期T，区域的基本信息J、Nj、C、D。

Step2：给定τ=1 时，供给和需求信息A1、Q1、L1、I1，以及区域的基本状态信息，状态变量I1=A1，根据Q1、L1、I1，计算c1，CA1，b1以及满足定理1 和性质1 的决策变量，将=0 作为新增约束条件，再根据整数规划的求解方法计算给出第1 个决策周期的分配方案X1。

Step3：若τ＜T，则：

（1）计算τ周期的状态变量Iτ=Iτ-1+Aτ-1-Zτ-1，根据Aτ，Qτ，Lτ，计算cτ，CAτ，bτ。

（3）重复步骤（1）～（2），直到τ=T，输出第T个决策周期的分配方案XT，计算终止。

（三）模型的拓展

平台在实际决策中考虑收益最大化的同时，通常还需要考虑保障平台的服务水平。服务水平由顾客的平均行走距离和被拒绝的顾客数量来衡量。由于共享平台的提出是为了充分利用闲置的车位以提高车位利用率，缓解停车难问题。因此当平台在进行τ周期决策时，需要考虑多目标决策。在综合考虑多个目标的情况下，将式（1）中的目标函数拓展为

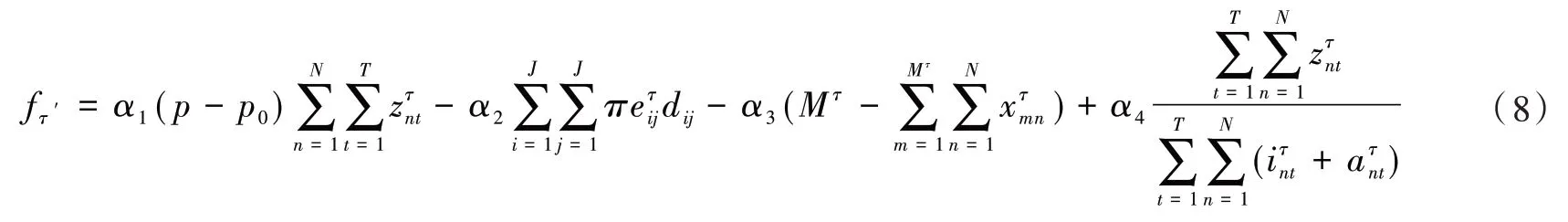
其中：α1，α2，α3，α4分别表示平台利润、步行距离的惩罚成本、被拒绝的顾客数以及车位利用率在决策中的权重。当单周期的目标函数为时，τ周期到T周期的总期望利润记为，则RDP的拓展模型为

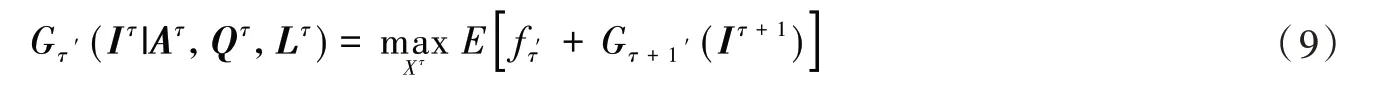
显然RDP的拓展模型维度也很高，很难进行精确计算，因此同样采用单周期分配策略进行近似计算，可得PSA的拓展模型为以下形式：

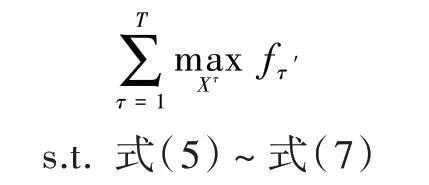
在拓展模型中既能保证顾客的满意度也能保证车位的利用率，因此拓展模型更具有现实意义。由于拓展模型的目标函数包含了各指标的权重，而权重的取值将会影响拓展模型的分配策略，因此权重的设定显得尤为重要。在实际问题中，权重的设定主要依赖于平台的经验和真实数据的收集，因此可以根据真实数据确定权重，再研究拓展模型的分配策略。

三、数值仿真

（一）算法有效性检验

由于RDP模型的维度较高，难以在有效时间内计算得到其最优解，无法与PSA模型进行对比检验，又由于PSA模型是假设平台不会将车位预留到后期以获得更高的收益，因此为检验该模型的有效性，本节将讨论确定性情况下（即假设在期初，平台已经知道后面每个周期新增的供给与需求信息）允许将车位预留到后期以获得更高收益的分配策略。若平台提前已知每个周期会新增的停车位供给与需求信息，则平台进行分配时将考虑是否将车位预留到后期以获得更高的利润。因此接下来首先构造一个模型对PSA的有效性进行检验。

1.检验模型的构建

若平台提前已知每个周期会新增的停车位供给与需求信息，则平台分配时可以考虑将车位预留到后期以获得更高的收益。若在τ周期，τ到T周期每个周期新增的停车位的供给与需求的相关信息Ak、Qk、Lk、k=τ，τ+1，…，T为已知信息，引用第二大节第（二）节的相关符号，则确定性分配策略模型为以下确定性线性规划模型（deterministic linear programming，DLP）：

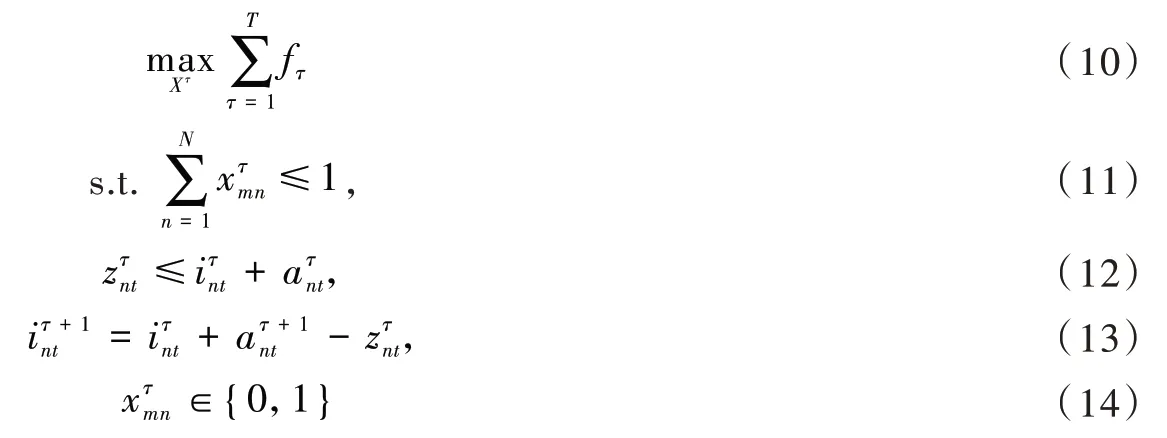
其中：m=1，2，…，Mτ；n=1，2，…，N；t=τ，τ+1，…，T；τ=1，2，…，T。

若令G=，分别用表示3 种模型最优策略下的G值。由于在DLP模型中，平台已经知道每个周期将新增的车位供给信息与需求信息，则平台在进行决策时可以根据所有的车位信息进行分配，因此，其分配策略集包含了PSA与RDP的分配策略集，所以有成立。在DLP模型中，每个周期的决策会影响下一个周期的决策，因此较PSA模型约束条件有所增加。根据PSA模型的矩阵形式很容易得到DLP模型的矩阵形式，不再赘述。接下来将采用数值仿真对PSA模型的有效性进行检验。

2.模型的有效性检验

为了探讨近似算法的有效性，将设计一系列的数值实验来验证单日近似分配算法的有效性。这里将DLP模型作为PSA模型有效性的检验。首先初始化参数，假设划分的区域共有3 个，3 个区域的停车位数量约为1/1/1，且每个周期车位供给的可能性是独立同分布的。假设dij=dji，且任意两个停车场的距离是服从［10，50］内的均匀分布。令s=p-p0表示停车位每成功出租一个周期平台获得的净利润，设置参数s=3，π=1。每个周期车位的需求和供给的开始时刻服从等可能分布，需求周期长度也服从等可能分布，在此假设下构造供给矩阵以及需求矩阵。

在验证算法有效性时，这里还考虑了DLP模型的极端情况，即所有的供给和需求均在进入决策周期之前已经全部提供，此时每周期不再有新增的供给和需求。平台在进行分配时，只需要根据供给与需求的信息进行静态车位分配（static parking space allocation，SP）。接下来将随机生成车位的供给和需求信息，分别在PSA模型、DLP模型、SP模型下分析不同的决策周期数以及车位数对目标函数的影响，图1～图4 均为运行50次后取均值得到的结果。

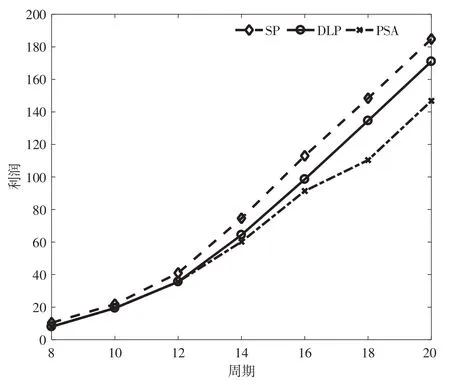
图1 不同决策周期数下不同模型的利润

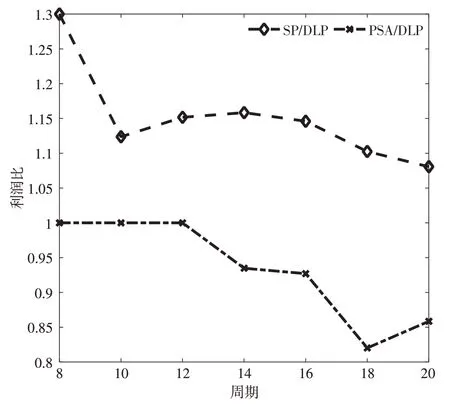
图2 不同决策周期数下不同模型的利润比

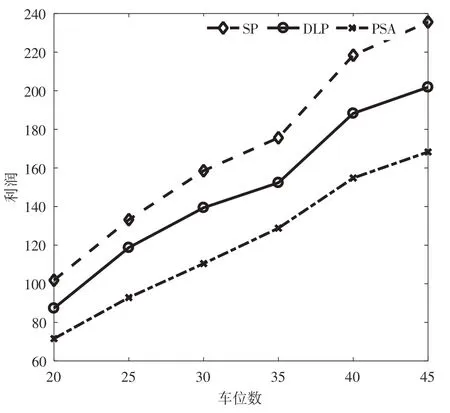
图3 不同车位数下不同模型的利润

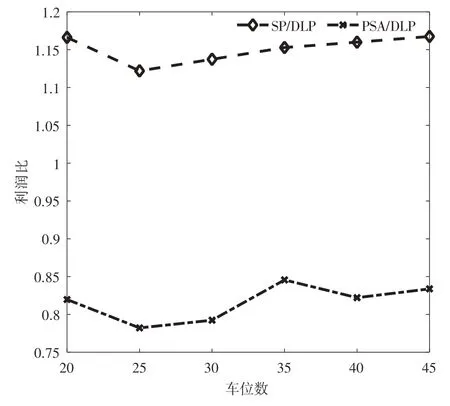
图4 不同车位数下不同模型的利润比

根据图1～图4，看出SP模型的利润总是高于DLP模型和PSA模型获得的利润，说明对于平台而言，若供给信息和需求信息能够提前提供，则可以减少决策时的不确定性，提高平台的利润，因此平台可以制订一些激励策略以促使需求者和供给者提前将信息发布到平台上，增加平台的收益。

（二）参数的灵敏度分析

由于PSA模型并未考虑车位利用率、顾客接受率、服务水平等，为从多个角度分析相关参数对PSA模型下分配策略的影响，接下来引入以下指标作为检验分配效果的标准。

（1）顾客接受率：接受率是指接受的顾客数与总的需求数的比率，因此接受率为。

（2）平均行走距离：由于行走距离会影响到顾客使用停车位的便利性，因此引入平均行走距离dˉ=来评估服务质量。

（3）停车位利用率：共享停车位提出的目的之一是为提高车位使用率，将顾客使用车位的总时间与供给者提供的总供给时间的比值作为停车位利用率的衡量指标，即。

（4）供需位置不同的车位指派率：由于本文考虑了行走距离带来的惩罚成本较低时，平台会将顾客指派到其他区域，因此引入供需位置不同的车位指派率（简称“车位指派率”）r=来刻画分配策略。

1.单位租赁利润对车位分配的影响

为研究单位周期净利润对车位分配的影响，将s取不同的值，重新参数设置如下：J=3，N1=35，N2=35，N3=25。距离为［10，50］上的均匀分布。取上述4 个指标的多次模拟的均值研究净利润变化对目标函数、接受率、平均行走距离、停车位利用率、车位指派率的影响。为研究考虑跨区域分配的有效性，选择顾客不接受步行的情况（即不允许需求为第i个区域的顾客分配到第j个区域）作为对比，结果见表1、表2。

表1 净利润对分配策略的影响（T=15）

表2 净利润对分配策略的影响（T=30）

根据表1、表2 可以看出PSA模型所获得的利润远高于仅将同一个区域的车位进行匹配时的利润。通过进行跨区域的匹配，有效地提高了车位的利用率和顾客的接受率，从而缓解了停车难的问题。在决策周期较短的情况下，随着价格的增加，车位指派率、接受率、车位利用率、行走距离会有所上升，且当价格对惩罚成本有绝对的优势时，其跨区域分配策略将不再受到价格的影响。由于PSA模型考虑的是当前周期收益最大化，在决策时未考虑后面的周期。因为当前周期的最大化决策可能会影响后面的周期，所以当周期较长时，车位指派率和停车位利用率并不完全是价格的单调函数，而是会受到每个周期的需求和供给的影响。

2.惩罚成本对车位分配的影响

考虑到车位异质性会影响顾客的满意度，而顾客的满意度以步行距离带来的惩罚成本衡量，惩罚成本越大，则说明车位的异质性程度越强，对顾客满意度的影响也越大。为研究车位异质性对分配策略的影响，这里将惩罚成本取不同的值，研究其对接受率，平均行走距离和车位利用率的影响。具体仿真结果整理见表3、表4。

表3 惩罚成本对车位分配的影响（T=15）

表4 惩罚成本对车位分配的影响（T=30）

根据表3、表4 可以看出，随着周期的增加，跨区域分配（PSA模型）的效果逐渐显著优于未进行跨区域分配的效果。当T=30 时，跨区域分配后得到的利润、顾客接受率、车位利用率均远高于未进行跨区域时的值。因此，当步行引起的惩罚成本较低时，采用跨区域分配优于直接根据区域进行匹配。随着惩罚成本的增加，即车位异质性增强，不同的车位对顾客的差异较大，则跨区域分配的收益逐渐减少，最终惩罚成本将会存在一个临界值，使得当超过该临界时，平台不会愿意进行跨区域分配。定理1 和性质1 给出了该临界值的下界，因此平台可以根据其下界，减少其分配方案，再进行决策。

平台每出租一个停车位的净利润与惩罚成本显著地影响了平台的分配策略。为进一步分析二者同时变化为平台决策带来的影响，下面将s与π同时变化，平台所获得利润以及跨区域分配比例的变化趋势如图5、图6 所示。

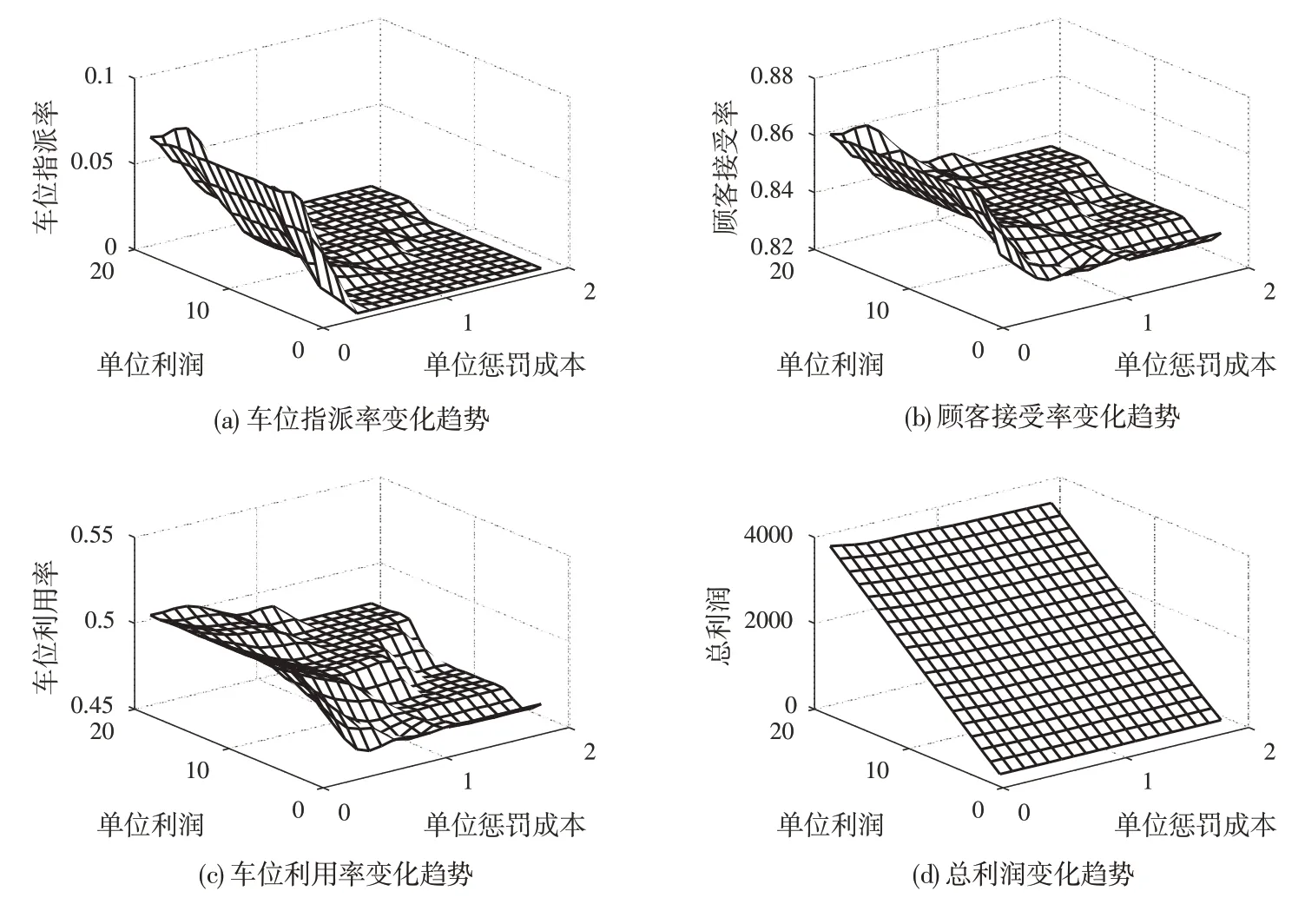
图5 T=15 时各指标变化趋势

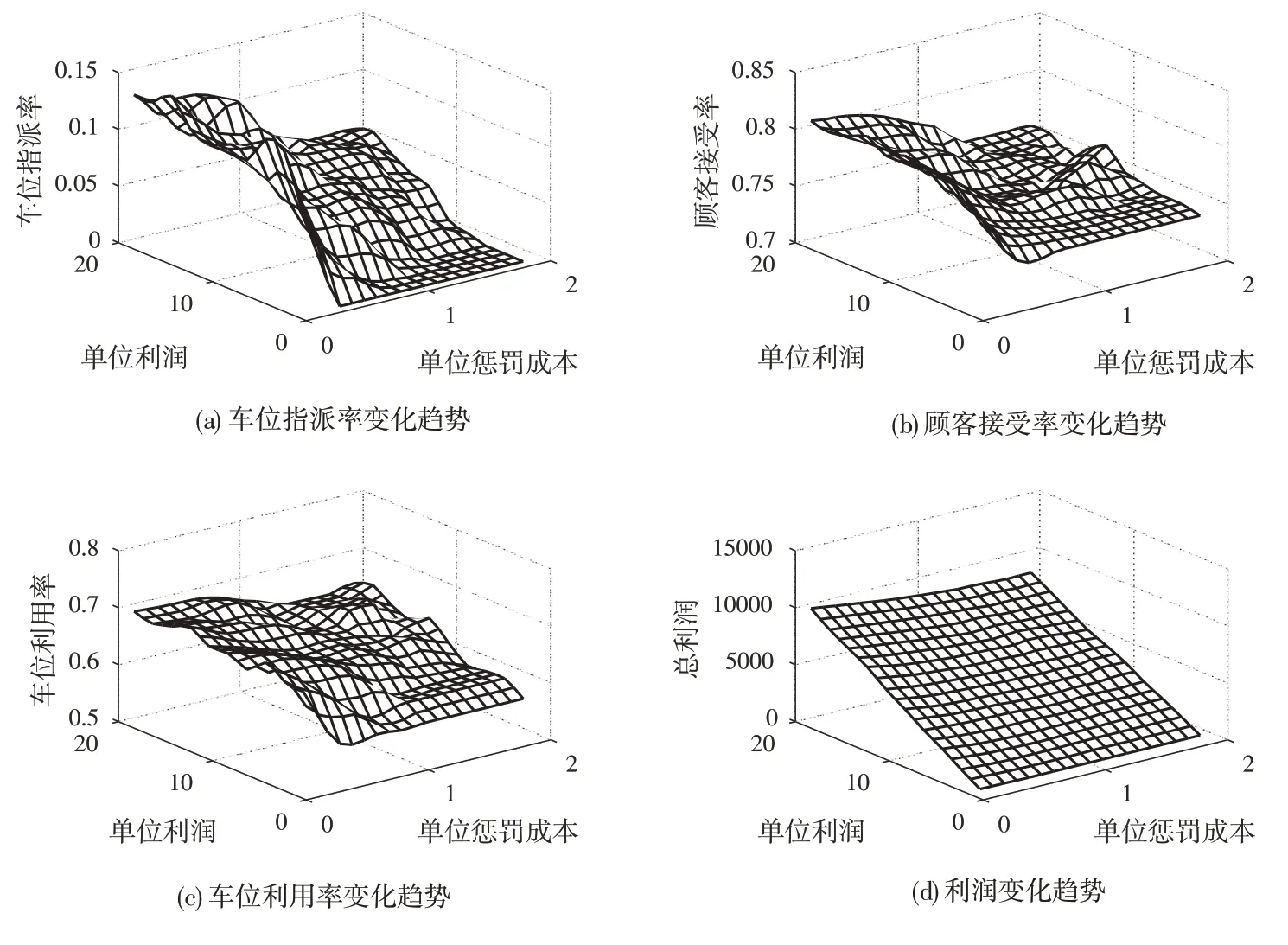
图6 T=30 时各指标变化趋势

根据图5、图6 可以得到，随着惩罚成本的增加，即不同位置车位对顾客的差异较大时，车位指派率将逼近于0，车位利用率以及车位指派率总体呈下降趋势。显然只考虑单周期决策时，车位利用率以及车位指派率是惩罚成本和单位收益的单调函数，但是随着决策周期的增加，车位利用率，车位指派率不再是惩罚成本和单位收益的单调函数。

在PSA模型中，当惩罚成本较低时，即不同位置车位对顾客差异较小时，车位利用率较高；不考虑跨区域分配时，车位利用率显著低于PSA模型的车位利用率，因此考虑跨区域分配能够有效地提高车位利用率缓解停车难问题，同时也可以有效地提高顾客接受率，减少顾客被拒绝的损失，因此平台在对顾客步行距离产生的惩罚成本进行较为精确的估计后，可以选择跨区域分配算法（该算法包含不进行跨区域分配的策略），该分配算法既可以提高平台的收益和顾客的接受率，也可以提高车位的利用率从而缓解停车难问题。

四、结论及展望

随着智能技术的出现，共享停车逐渐出现在人们的日常生活中。本文首先根据车位异质性对顾客的影响，对车位位置划分区域，构建了当供给者和需求者动态地向平台提供信息时的随机动态规划模型，并分析得到了车位分配的基本原则。由于原始模型求解的复杂度过高，因此根据车位基本分配原则设计单周期近似分配算法对问题进行求解，最后构建检验模型，采用数值仿真验证了近似分配算法的有效性以及异质性对分配策略的影响程度。研究得到若供给信息和需求信息可以提前提供给平台，则可以减少决策时的不确定性，提高平台的利润；在决策周期较短的情况下，随着惩罚成本的降低或者单位租赁净利润的增加，车位的利用率和车位的指派率等均会上升；随着决策周期的增加，车位利用率、车位指派率和平均行走距离却并非惩罚成本与单位租赁净利润的单调函数。考虑跨区域分配能够有效地提高车位利用率、顾客接受率以及平台的收益，从而既保障了平台的收益也缓解了停车难问题，对于共享平台的管理实践具有一定的指导意义。但是值得注意的是若惩罚成本较大，即车位异质性较强时，平台将不愿意进行跨区域分配。

除此之外，还可以从以下3 个方面进行拓展研究：

（1）车位需求者的异质性。实际上，顾客对于车位异质性的敏感程度也具有差异性。如有的顾客对于停车后的行走距离敏感性较强，用较远车位去满足该顾客，其不满意度较大；而有的顾客对于停车后的行走距离敏感性较弱，则用较远车位满足该顾客时，不满意度将小于敏感性较强的顾客。因此，顾客对车位异质性的敏感程度将影响车位的分配决策，接下来可进一步研究车位需求者具有异质性的前提下，车位的分配决策策略。

（2）总车位供给量随机。在总车位供给量已知的前提下，研究不同时间段提供的车位具有随机性的车位分配。因此，总车位供给量随机时的车位的分配决策问题可作为进一步研究的方向。

（3）动态定价。假设车位的价格是固定的，在实际生活中，价格是影响顾客需求的重要因素，平台可通过设置不同时间的车位价格来调节车位的供需匹配问题，因此车位动态定价与车位分配的联合决策问题也是未来的研究方向。