基于状态观测器的动态事件触发机制

朱明健,樊 渊,张成笑

(安徽大学 电气工程与自动化学院,合肥 230601)

0 概述

在传统的时间采样控制系统中,系统状态采样和控制器的更新通常是周期性进行的。当计算和通信资源需要分配给其任务时,这种时间触发的方式可能使系统处于高工作负载状态。为了节省系统资源,可以采用非周期性的触发方法。近年来,人们越来越关注事件触发的反馈控制系统。文献[1-3]描述了关于事件触发机制的一些基本概念。事件触发机制是时间触发机制的替代方案,在事件触发的方案中,一旦检测到系统状态偏差不满足给定的事件触发条件,就会触发控制任务[4-5]。与时间触发机制中的周期状态采样方式不同,事件触发中的状态采样是非周期性的。因此,设计控制器使得其仅在必要时使用计算和通信资源,可以减少对系统资源的占用,同时保持良好的稳定性能。研究结果表明,事件触发机制相较于时间触发机制具有更优的资源节省性能。目前,多数研究致力于开发设计事件触发机制(ETM)的系统技术,用于实现给定反馈控制器的系统稳定[6],最常用的ETM通常由给定系统状态的等式或不等式组成。事件触发机制多采用文献[7-8]中的多智能体系统,也常见于多智能体系统的自触发方案设计[9-10]。

文献[11]研究了基于观测器的事件触发控制的闭环系统。类似于事件触发的输出反馈控制系统的情况[12],该系统的输出仅在满足事件触发条件时传输给观测器。通过满足给定的线性矩阵不等式(LMIs)条件和事件触发条件,可以使反馈控制系统和观测器系统是渐近稳定的。文献[13-14]研究了在某些不确定系统中基于观测器的事件触发状态反馈机制,通过求解LMIs可以证明系统的稳定性。

通过在事件触发机制中引入一个内部动态变量,可以得到动态ETM。已有研究学者对ETM中的内部动态变量进行了研究[15-17]。文献[18-19]中的动态触发机制也引入了内部动态变量,且提出的机制已经获得了相应的理论成果。与ETM相比,动态ETM可以降低收敛速度和触发次数,从而改进ETM的性能。事实证明,对于大部分事件触发控制器而言,动态ETM的最小触发间隔大于ETM[20]。

对于多数事件触发机制研究来说,系统状态都是已知的。本文针对状态不可测线性系统,提出一种基于状态观测器输出反馈的动态ETM,状态观测器利用输出的事件触发信号来估计系统状态。事件触发的控制系统可能会存在Zeno行为,Zeno行为意味着在有限的时间段内存在无数次的触发,这对于实际物理系统是不允许的。因此,在实验中给出事件触发控制的最小触发时间间隔,以排除Zeno行为。

1 基础知识

函数f:Rn→Rm使得对于任意的x,y∈Q⊂Rn,存在一个常数矩阵M>0且满足式(1)时,则称该函数是Lipschitz连续的。

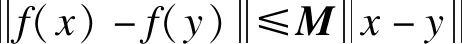
(1)

其中,Rn表示n维欧式空间,Rm×n表示所有的m×n维实矩阵的集合。

引理1[21]若X和Y是实正定矩阵,则以下不等式成立:

XTY+YTX≤XTX+YTY

(2)

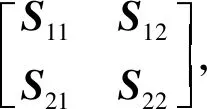
2 基于观测器事件触发机制

系统状态空间表达式为:

(3)

其中,x∈Rn为系统的状态向量,初始状态定义为x(0)=x0,u∈Rm为系统的输入向量,y∈Rq为输出向量。A∈Rn×n,B∈Rn×m和C∈Rq×n均为已知常数矩阵。全维状态观测器为:

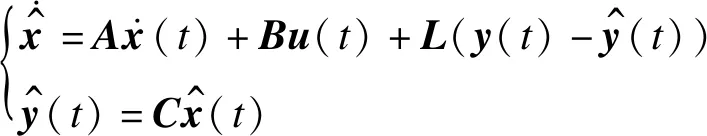
(4)

2.1 事件触发机制

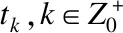
定义输出误差为:

ey(t)=y(tk)-y(t),t∈[tk,tk+1)

(5)

因此,可以描述系统状态和观测器状态误差为:

(6)

事件触发机制系统结构如图1所示。

图1 基于观测器的事件触发机制系统结构Fig.1 Event triggering mechanism system structure based on observer

定义事件触发条件为:

(7)

其中,σ为给定的常数。当不满足式(7)时,对系统输出信号进行更新。

定理1在系统式(6)中,如果存在2个正定矩阵P1,P2∈Rn×n,以及正数σ∈[0,1)满足以下2个矩阵不等式(8)与式(9):

(8)

(9)

证明构造Lyapunov函数为:

其中,P1,P2分别为矩阵不等式(8)和式(9)的解,对Lyapunov函数关于时间求导可以得到:

xT(t)(P1(A+BK)+(A+BK)TP1)x(t)+

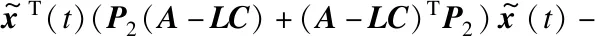
xT(t)(P1(A+BK)+(A+BK)TP1)x(t)+

(10)

由事件触发机制可知,若式(7)不满足,则会有第k+1次更新执行。因此,通过计算可以得到:

P1BKKTBTP1+σCTC)x(t)+

(11)

由引理1可知,不等式(8)、不等式(9)分别与以下不等式(12)、不等式(13)等价:

P1(A+BK)+(A+BK)TP1+

P1BKKTBTP1+σCTC<0

(12)

P2(A-LC)+(A-LC)TP2+

P2LLTP2+I<0

(13)

近稳定的。

备注1通过求解线性矩阵不等式(8)和不等式(9),可以得到参数σ以及P1和P2的值。这些参数值在事件触发条件式(7)下可以保证系统状态和观测器误差状态的渐近稳定性。此外,这2个线性矩阵不等式互相独立。事件触发策略的设计仅仅与控制器增益矩阵K有关,而与观测器本身无关,这显示了事件触发方案的设计与观测器之间的分离原则。

令2个对称正定矩阵M,N∈Rn×n满足以下等式:

M=-(P1(A+BK)+(A+BK)TP1+

P1BKKTBTP1)

(14)

N=-(P2(A-LC)+(A-LC)TP2+

P2LLTP2+I)

(15)

可以得到:

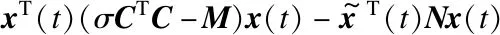
(16)

(17)

2.2 动态事件触发机制

通过使用动态ETM,系统可以进一步减少触发次数,从而可以实现更好的资源节省性能。基于满足以下微分方程的内部动态变量η引入动态ETM:

η(0)=η0

(18)

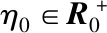
(19)

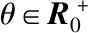
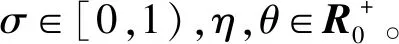
(20)

η(t)≥0

(21)

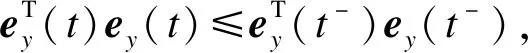
(22)

通过式(18)可以得到:

(23)

通过比较和分析可知,对任意的t∈[0,∞)都满足η(t)≥0,因此,η在任意时刻都保证是非负的。

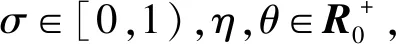
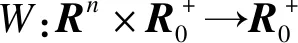
(24)

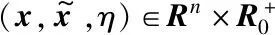
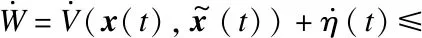
σyT(t)y(t)-β(η(t))=

xT(t)(σCTC-M)x(t)-

(25)

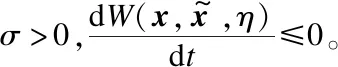
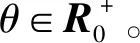
2.3 Zeno行为分析

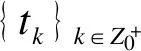
(26)

令:

(27)

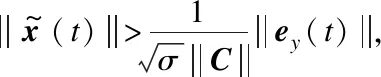
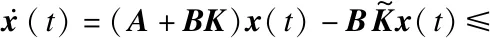
(28)

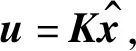
(29)

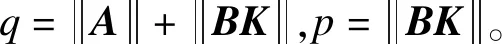
证明利用式(28)的结论,可以通过以下变量的导数得到触发间隔下限:

(30)

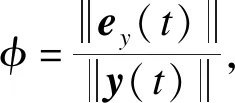
(31)

令初始条件为φ(0)=0,通过求解式(31)可以得到:

(32)

因此,可以得到事件触发最小时间下界τ为:

(33)

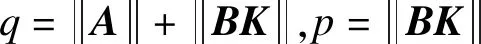
(34)

(35)

因此τ>0。事件触发机制不存在Zeno行为。

推论表明,对于系统给定的状态,动态ETM给出的下一个执行时间大于ETM给出的时间。

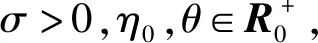
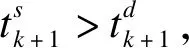
(36)

当θ>0时,由式(19)和引理3可以得到:

(37)

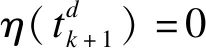
3 模拟仿真

使用一个例子来验证理论结果的有效性。考虑形式为式(3)的线性系统为:

系统很明显是完全可控可观的。

实验选取β(η)=λη是满足Lipschitz连续的K∞函数。关于λ和θ的参数,为了显示更好的效果,参数选取为λ=0.01,σ=0.003 1和θ=1。这些参数选取符合具有动态触发机制的事件触发机制要求。

图2显示了ETM的误差范数,误差范数一旦达到阈值,它就会重置为0。图3显示了动态ETM的误差范数,当误差范数达到阈值时,它也会重置为0。从图中可以看出,动态ETM可容许较大的误差范数阈值,这是由事件触发条件决定的。ETM的触发次数为201,动态ETM的触发次数为30,与ETM相比,动态ETM减少了触发次数。

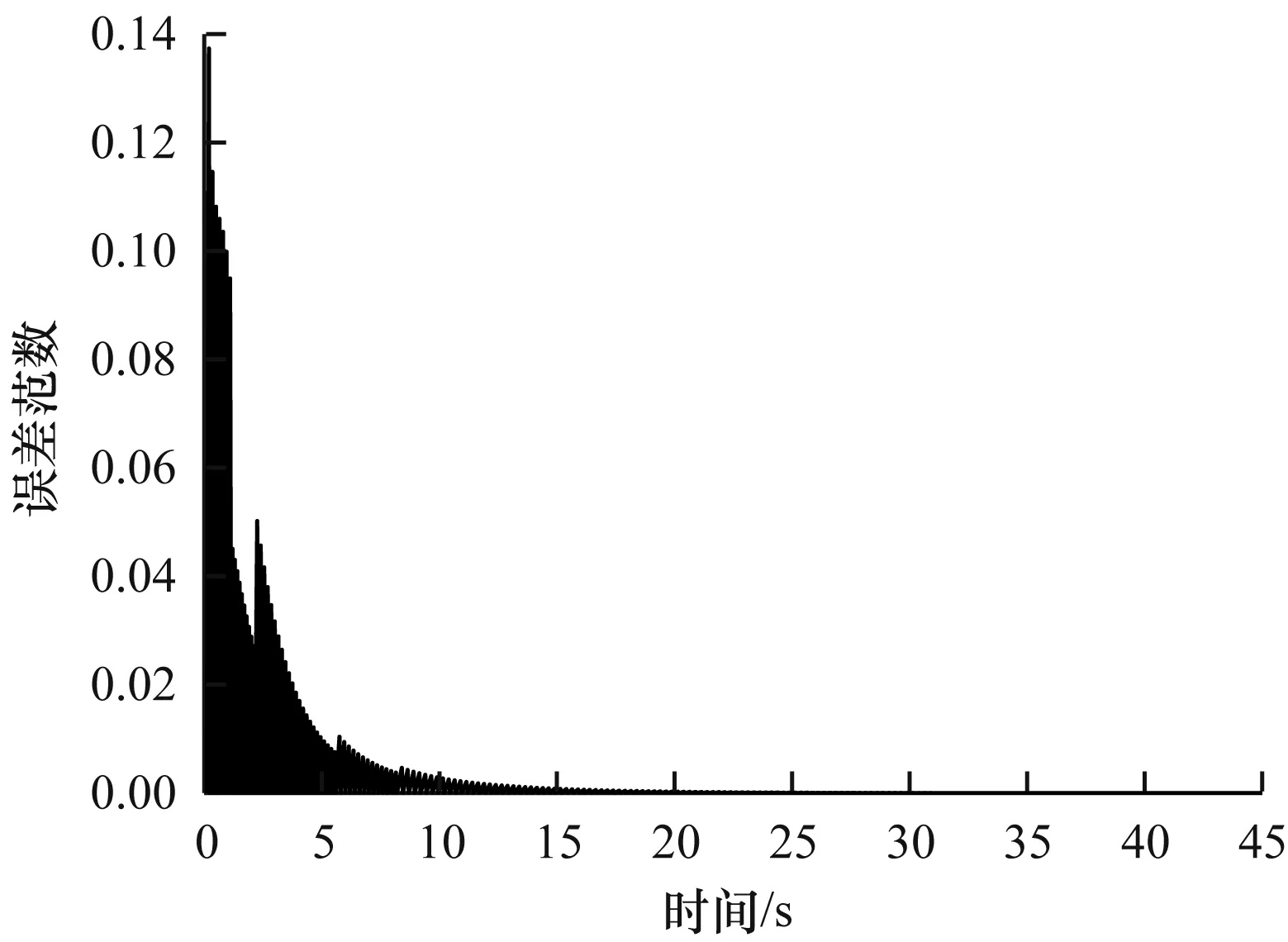
图2 ETM误差范数Fig.2 ETM error norm

图3 动态ETM误差范数Fig.3 Dynamic ETM error norm

基于观测器ETM的平均触发时间间隔如图4所示,触发时间间隔的平均值为0.224 s。图5所示为基于观测器的动态ETM事件触发机制的平均触发时间间隔,平均触发时间间隔为1.500 s。 ETM的触发时间间隔的平均值远小于动态ETM的平均触发时间间隔。

图4 ETM触发时间间隔Fig.4 ETM trigger the interval

图5 动态ETM触发时间间隔Fig.5 Dynamic ETM trigger time interval

图6、图7和图8中的状态轨迹展示了基于观测器的动态ETM事件触发机制系统的渐近稳定性。 图6显示了系统的状态轨迹,从图6可以看出,系统的状态由初始值[-0.2,0.4]逐渐趋于原点,系统是渐近稳定的。图7显示了观测器的状态轨迹,从图7可以看出,观测器的状态由初始值[0,0]逐渐逼近系统实际状态,且最终趋于稳定。图8显示了观测器误差的状态轨迹,在初始时刻,针对状态不可测现象,令观测器状态和系统实际状态初始值不同,因此观测器误差较大,随着系统的运行,误差可以迅速减小并趋于0。

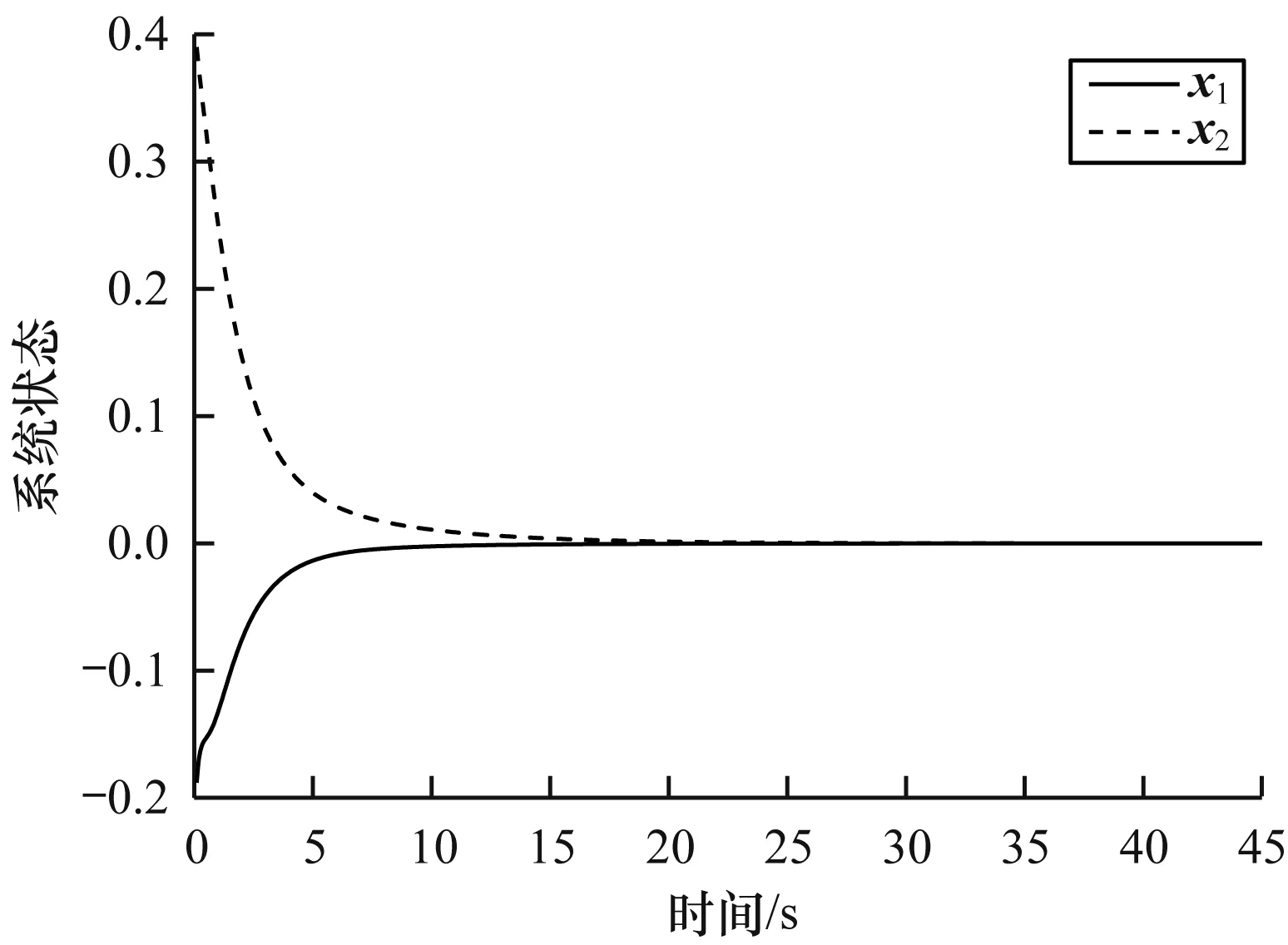
图6 动态ETM系统状态轨迹Fig.6 Dynamic ETM system state trajectory

图7 动态ETM观测器状态轨迹Fig.7 Dynamic ETM observer state trajectory

图8 动态ETM观测器状态误差轨迹Fig.8 Dynamic ETM observer state error trajectory

4 结束语

本文提出一种基于观测器的动态事件触发机制,根据2个LMIs建立系统渐近稳定的条件。通过引入额外的内部动态变量,事件触发条件会更加多样化,从而减少事件触发次数。本文给出了Zeno 行为不存在的证明过程,并通过仿真实例论证结果,这些实例可应用于线性时不变系统。下一步可以考虑改善事件触发条件和加入优化控制,以期达到优化系统性能指标的目的。