土层模型参数变异性对场地地表地震动的影响分析
冯伟栋,曹均锋,彭刘亚,王德才
(1.安徽省地震局, 安徽 合肥 230031;2.合肥工业大学建筑与艺术学院 ,安徽 合肥 230009)
0 引言
历次地震如唐山、汶川等地震震害及其强地面运动观测结果表明,场地地表地震动差异性主要受地震震源特性、地壳岩石圈地震动传播差异性及局部场地条件如地形、覆盖层差异性等的影响,其中同一次地震且距离较近的场址震害异常或地震动差异的主要原因是局部场地条件的差异性带来的。究其机理,主要是因为场地土层刚度和动强度的差异及地形变化,使其地表地震反应差别明显,进而直接影响地震灾害的分布和影响程度。因此获取场地相关的设计地表地震动参数十分必要。指导工程抗震设计用的场地地震动参数确定方法主要有两类:(1)通过统计分析历次地震中获取的强震记录,获取场地相关的地震动输入;(2)直接进行局部场地地震反应分析以获取与该场址土层结构相关的设计地震动参数。由于第(1)种方法需要统计的数据量较大,且不一定能获取到与目标地震动输入相关的场地相关地震动,因此第(2)种方法指导抗震设计中应用更为广泛。
局部场地地震反应分析中,充分考虑土层结构、土体非线性、场地相关的输入基岩地震动及人工边界条件以建立合理的地基土层模型,是场地反应分析结果可行的重要前提[1-5]。然而,土层模型的建立受土层剪切波速、输入界面的选取、分层厚度的确定等诸多因素的影响,不同的土层模型将会直接影响场地地表地震动幅值及其频谱特性。本文以某华东地区典型钻孔剖面为对象,构建了多种计算模型,分析土层剪切波速、输入界面位置及输入界面剪切波速、分层厚度等多种土层模型参数差异性对场地地震动参数的影响范围和规律,以期能对抗震设计用场地地震动参数获取提供一定的参考。
1 计算方法
近年来,随着计算机技术的高速普及,局部场地条件地震反应分析得到了长足的发展,波动(及振动)分析法、频域等效线性化法和时域直接积分法等是其典型代表。等效线性化法因适用性强、计算效率高已成为应用最广泛的方法。该方法基本原理如下:
假设将土层模型简化为上卧于弹性半空间上若干水平成层的土层构成,并假设地震波从基底垂直入射到上覆粘弹性水平土层介质中,介质土层满足如下波动方程:
(1)
uj(zj,t)=Uj(zj)eiωt
(2)
Uj(zj)=Ejeikjzj+Fje-ikjzj
(3)
式中,uj(zj,t)、ρj、Gj、ηj分别为第j层土的位移函数、密度、剪切模量、粘滞系数。式(3)中第一项为由土层下向上传播的入射波,第二项由土层上向下传播的反射波。
各土层界面间需满足的位移连续和应力连续条件如下:
uj(zj,t)|zj=hj=uj+1(zj+1,t)|zj+1=0
(4)
τj|zj=hj=τj+1|zj+1=0
(5)
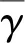
(6)
(7)
基于以上假设,等效线性化一维土层地震反应分析法的实施步骤如下:
(1)将基岩入射波进行傅里叶变换;
(2)假定某一初始剪应变,计算单一简谐波输入下土层的传递函数;
(3)将计算所得土层传递函数与基岩入射波的傅立叶谱相乘后进行傅立叶反变换,从而得到土层地震反应的时域加速度及剪应变时程;
(4)对比计算所得等效剪应变与初始假定剪应变相对误差,若误差大于规定值(如5%),则利用计算所得等效剪应变值作为重新假设的初始剪应变,再次计算土层传递函数,然后重复(3)的步骤,直到计算所得等效剪应变与计算开始时假定剪应变相对误差小于规定值为止,并最终获取土层地震反应的时域加速度、剪应变曲线及反应谱等其他结果。
2 计算模型及输入地震动
2.1 计算模型
选取华东地区某典型土层剖面作为计算模型,土层剖面参数见表1。该剖面的覆盖层厚度为42.3m,主要由填土、粘土、中粗砂和砂岩组成,属于Ⅱ类场地。土层动力参数主要是通过现场取样并进行动三轴试验得到的,部分土层动力参数采用经典推荐值[6]。

表1 基本剖面参数
2.2 输入基岩地震动
考虑到地震动频谱特征的差异性,选取了不同频率成分的3条强震记录(Taft、Kobe和E1centro)作为基底地震动输入,地震动持时均为40s。为了方便对照,研究中将强震记录幅值分别按照50、100、200、400gal进行等比例调整,并将调整后的幅值缩小一半作为基底地震动的输入。
3 分析与讨论
3.1 土层剪切波速的影响
土层剪切波速直接反映土体动刚度,其差异性会直接影响场地地震反应的差异性。目前,土层剪切波速主要是通过原位测试得到的。但是原位测试获取的剪切波速结果受测试方法、仪器精度、人工操作等方面的差异性的影响。本文分析了剪切波速的不确定性对场地地震动的影响程度,将实测土层剪切波速增大或减少5%、10%、15%、20%,共建立9个对比计算模型,选取幅值调整后的12组地震动记录作为基底输入地震动,得到了108个工况下的Amax及Tg的均值,如表2所示。其中反应谱的放大系数βm统一取2.5,反应谱特征周期Tg取反应谱平台值与其右相交点的横坐标[7]。
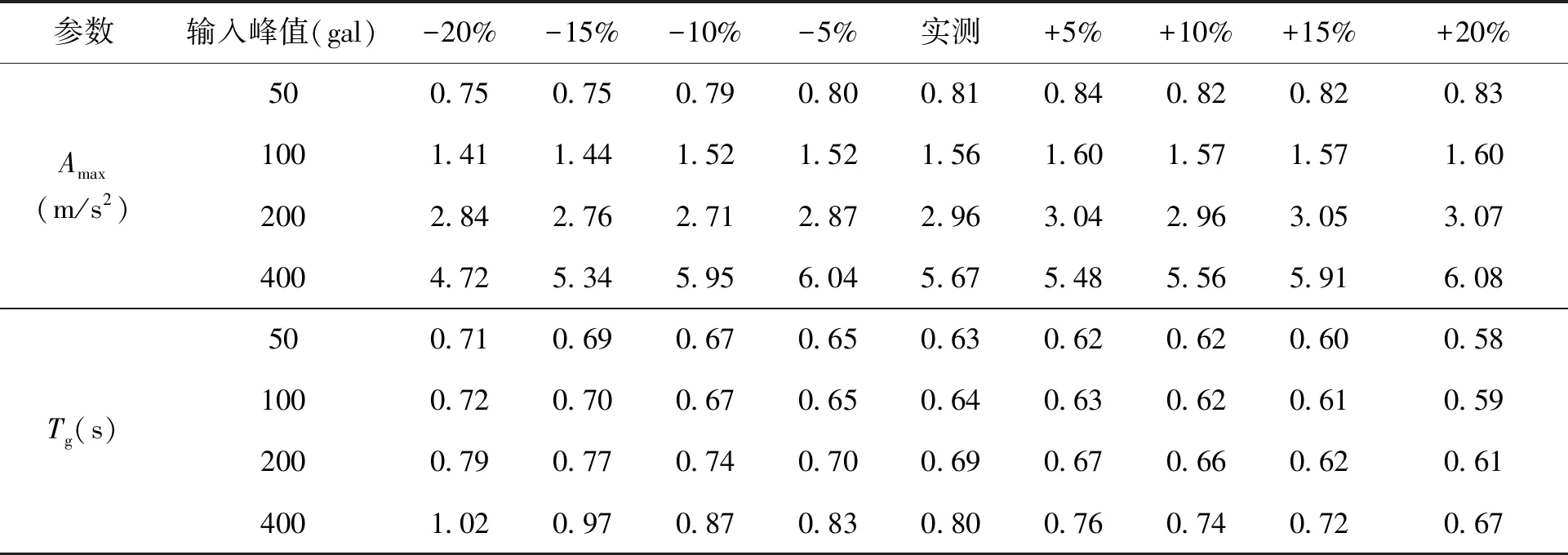
表2 不同土层剪切波速下的地表地震动参数
图1给出了增减剪切波速值模型计算结果与实测波速模型计算结果的相对偏差。由图1可知:(1)将实测波速值模型在20%范围内增减时,地表峰值加速度Amax和地表加速度反应谱特征周期Tg计算结果与实测波速值模型计算结果与模型波速值Vs的增减呈一定的相关性,Vs差异性越大,其Amax和Tg的变化也越大。(2)Amax与Vs呈正相关,Vs减小,Amax也逐渐减小,当输入峰值为400gal工况中,Vs降低20%时,Amax减小约17%;Vs增大,Amax也逐渐增大;当输入峰值为400gal工况中,Vs增大20%时,Amax增大约7%。(3)Tg与Vs呈负相关,当Vs减小时,Tg增加,当输入峰值为400gal工况中,Vs减小20%时,Tg增大约0.22s;当Vs增大时,Tg会减小;当输入峰值为400gal工况中,Vs增大20%时,Tg降低约0.13s。(4)Vs减小对Amax、Tg的影响比Vs增大时影响程度要略大一些。(5)Vs的变异性对地表地震动的影响程度受基底输入地震动幅值的影响明显,随着输入地震动幅值增大,Amax和Tg的差异也逐渐增大,当Vs降低20%时,输入峰值从50gal逐渐增大到100、200、400gal时,其Amax减小量分别为7%、10%、4%、17%,Tg的增大量分别为0.08s、0.08s、0.10s、0.22s。
3.2 输入界面选取的影响
一维土层地震反应分析中包含一个基本假定,即地震动输入界面为基岩弹性半空间与土层交界面,但是由于地层变化的连续性这一理想假设并不成立,工程上通常将输入界面选取在基岩顶面或剪切波速大于500m/s的土层顶面[8-10]。但是,在场地覆盖层中包含较厚的强风化岩层且风化岩层界限并不明确时,终孔土层并不一定能够满足作为输入界面的要求[11-12],本研究将对输入界面在较厚的风化岩层界限里变化时对场地地震动参数带来影响进行研究。
3.2.1 输入界面位置的影响
本研究选取表1中给出的较厚的强、中风化岩层的不同深度位置作为地震动输入界面(表3),分析了输入界面变异性对场地地震动参数的影响,研究中设置了5个不同界面位置,并在输入界面处输入调整幅值的Kobe地震动,综合研究了输入界面变化对地表峰值加速度Amax和地表加速度反应谱特征周期Tg的影响。

表3 输入界面的参数
图2为不同输入界面模型的地表加速度反应谱分布,由图2可以看出:(1)随着输入界面的埋深增加,地表加速度反应谱值逐渐增大,但增幅逐渐减小;(2)输入界面埋深较深时,反应谱主要在1.0s以内变化,且周期越短变化越显著;(3)输入界面的变异性影响程度受输入基岩地震动幅值的制约,输入地震动幅值越大,反应谱差异性也越大。
以波速554m/s的中风化砂岩输入界面模型的(界面5)计算结果为基准,表4给出了不同输入界面计算模型计算结果的相对偏差。从表中可知:(1)随着输入界面埋深增加,场地地表峰值加速度Amax逐渐增加,但增幅逐渐减小;界面深度变化对地表加速度反应谱特征周期Tg的影响不明显。(2)当选取输入界面选择在剪切波速超过450m/s土层时,输入界面位置变化对计算结果相对差异基本可控制在10%以内,这表明如仅考虑Amax、Tg的大小时,若输入界面所处的土层剪切波速超过450m/s,其输入界面位置的选择标准可适当放宽。
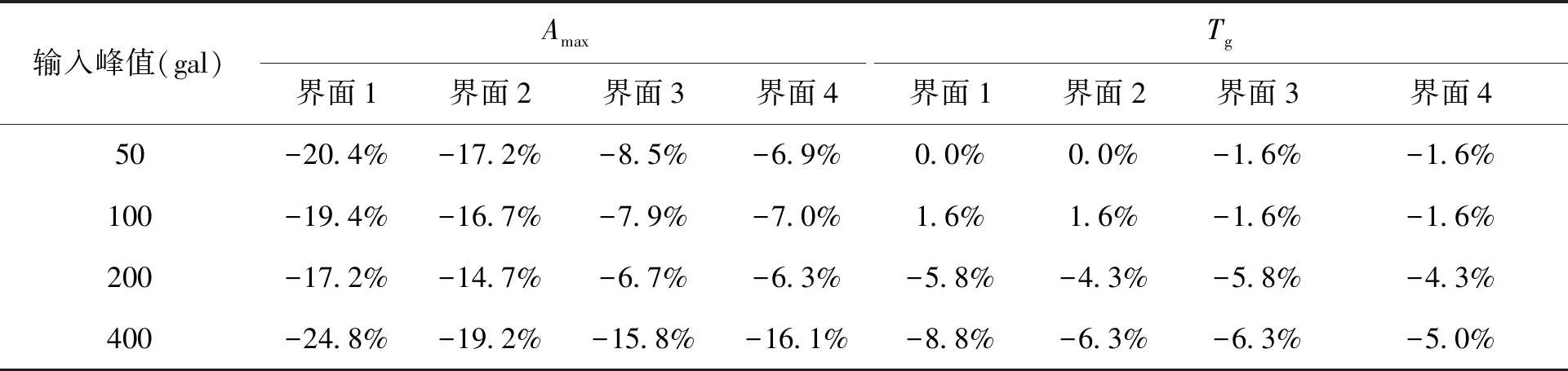
表4 不同输入界面计算结果对比
3.2.2 输入界面剪切波速的影响
已有研究表明,基底输入界面剪切波速值变异性对场地地表地震动参数变异性有一定的影响[9]。本研究以波速554m/s的中风化砂岩输入界面模型的(界面5)计算剖面作为参考模型,在500m/s至800m/s之间调整输入界面剪切波速Vsj值以建立7个不同的计算模型,并在输入界面处输入4中不同幅值的基岩地震动,以定量分析的方式分析输入界面剪切波速变异性对场地地表地震动参数变异性的影响。
各模型地表峰值加速度Amax及反应谱的特征周期Tg如图3所示。由图3可以看出:(1)输入界面剪切波速Vsj对地表峰值加速度Amax影响较为显著,随着Vsj增大,Amax也逐渐增大;(2)输入界面剪切波速Vsj的变化对地表加速度反应谱特征周期Tg影响有限,当基底输入地震动峰值较小时,Tg基本不随Vsj的增加而变化。
为进一步分析输入界面剪切波速Vsj变化对地表地震动峰值Amax的影响,我们以Vsj取500m/s模型为基准,分析了输入界面剪切波速变异性对地表峰值加速度Amax变异性的相对影响,结果表明,Amax随着Vsj的增大而增大,且两者的增幅呈现近似的线性关系(图4),例如,基岩输入峰值200gal条件下,当Vsj增加10%时(即550m/s),Amax增加3.3%,当Vsj增加40%时(即700m/s),Amax增加13.2%。
3.3 分层厚度的影响
按照等效线性化计算框架,构建土层模型时,不同的分层厚度会对地表地震动参数构成一定的影响。研究中考虑了按照1.0m、2.0m及相同土层不分层的3种分层模型,在输入界面处输入调整幅值的Kobe地震动作用下,分别分析了不同的地震动幅值下分层厚度对地表地震动峰值和反应谱特征周期的影响。
表5给出了不同输入地震动幅值下地表地震动加速度峰值Amax及加速度反应谱特征周期Tg随不同土层模型分层厚度变化的关系。结果表明:(1)分层厚度变化对会影响地表地震动参数,相同土层不分层厚度模型的Amax和Tg相对偏低,偏于不安全,因此构建土层模型时应尽可能将各土层进行细分;(2)1.0m和2.0m分层厚度土层模型的地震动峰值及反应谱计算结果基本一致,因此2.0m的分层厚度能合理反映土层地震反应分析的结果。

表5 不同分层厚度下的地表地震动参数
4 结论
以华东地区某典型钻孔II类场地土层模型为对象,采用频域等效线性化法分析了地基土层剪切波速、输入界面位置及波速选取、分层厚度等模型参数变异性对场地地表地震动幅值和谱特征的影响。研究结果表明,土层模型参数的变化对地表地震动参数有显著影响,具体表现为:
(1)地表地震动加速度峰值Amax与土层剪切波速Vs呈正相关,地表加速度反应谱特征周期Tg与土层剪切波速Vs呈负相关,Amax随Vs减小而减小,Tg随Vs减小而增加,当输入峰值为400gal工况中,Vs降低20%时,Amax减小约17%,Tg增大约0.22s。
(2)场地地表峰值加速度Amax随输入界面埋深的增加逐渐增加,输入界面剪切波速Vsj的变化对Amax影响较为显著,Amax随着Vsj的增大而增大,且两者的增幅呈现近似的线性关系,当基岩输入峰值200gal条件下,Vsj增加10%时Amax增加3.3%,当Vsj增加40%时Amax增加13.2%;但输入界面埋深变化及输入界面剪切波速的变化对地表加速度反应谱特征周期Tg的影响有限。
(3)分层厚度较大的土层模型计算得到的场地地表地震动Amax和Tg相对偏低,这将使获取的设计地震动偏于不安全,因此构建土层模型时应尽可能将各土层进行细分;1.0m和2.0m分层厚度土层模型的地震动峰值及反应谱计算结果基本一致,因此为了提高计算效率,可以认为2.0m的分层厚度能合理反映土层地震反应分析的结果。
(4)地基土模型参数的变异性影响程度与输入基岩地震动幅值有关,总体上表现为随着输入基岩地震动峰值增大,Amax和Tg的差异也增大。
后期研究将针对更多的土层剖面开展更加细致的研究,并进一步分析不同场地类别下土层模型中土层剪切波速变化、输入界面位置变化、输入界面剪切波速变化、分层厚度变化对地表地震动峰值及反应谱特征周期的影响,并分析其变化对统计学特征参数的定量分析。
致谢:感谢编辑部老师及匿名审稿专家对本文提出的诚恳意见,您的努力使本文表述变得更加准确和规范。

