雷达渐消IQ失衡回波信号的匹配滤波器设计

陆泽橼 程超才 王金峰 于秋野 徐海洲 朱子平

(中国电子科技集团公司第三十八研究所 合肥 230088)

0 引言

无线电信号在收发过程中，因为实际微波系统参数偏离设计理想参数，所以会出现IQ失衡、直流分量和非线性相位等现象。其中IQ不平衡在雷达中会导致信噪比下降、目标位置测量偏差和大量虚警检测等严重后果。

为了降低IQ不平衡，一方面可以通过使用添加模拟补偿电路的方式解决，但是这些技术对于已经完成投产的装备改造来说，不具有成本和功耗上的优势；另一方面可以通过数字信号处理对IQ不平衡估计和补偿，现有几种典型数字域IQ估计补偿方法如下。

第一类认为体系具有时不变性，通过适当选取训练序列[1-2]和相应的检测算法[3]，对时不变的 I/Q 失衡进行补偿。具有简单高效的优点，但需要增加包括检测和校正的工作模式，导致系统实时性不足，且需要雷达系统收发多个过程配合，占用了系统资源。

第二类是基于信号统计学特性[4-5]的 I/Q 失衡补偿，包括干扰消除法(IC)、最小均方算法(LMS)和递归最小二乘法(RLS)，利用接收信号的随机特征，该方法无需训练序列的辅助，可用于频率选择性 I/Q 失衡的补偿，缺点是存在信号泄漏的问题，计算开销大，耗费系统资源。

第三类是基于自适应盲源分离法[6-7]，不需要导频或训练信号等先验信息，利用源信号的频率非依赖性，对合成信号进行分离，增强输出信号干扰比，但是盲估计需要大量信号确定特征，且为了获取的参数稳定可靠需要长时间迭代过程。

第二类和第三类方法都采用了数字域校正，包括幅度相位校正：幅度校正通过乘除校正因子实现，具体是在数字域芯片中采用移位运算；相位校正通过投影原理实现，相位误差使得IQ两路信号不正交。可固定其中一路I或Q，使另外一路Q或I信号向正交坐标轴投影，使相位校正后基带信号正交。

随着阵列天线及MIMO技术的不断发展，IQ失衡对MIMO系统性能影响的研究[9-10]得到开展。发射机[10]和接收机[11]中各自存在的IQ失衡问题也得到了研究。目前IQ失衡研究主要集中在通信系统，数字相控阵雷达[12]在特定工作模式下，由发射和接收共同产生的IQ失衡，通过回波数字信号处理抑制的方法未得到深入研究。典型的三类数字域IQ 失衡补偿方法，需要对雷达工作模式进行修改，或计算耗费太大，本文拟通过滤波设计方法解决回波IQ失衡问题，采用滤波方法不增加硬件设备，不需要增加额外的工作模式，计算耗费小，具有良好的工程应用前景。

1 雷达回波IQ失衡的数字信号处理

根据数字阵列雷达的信号特点，对IQ失衡回波进行建模，其中根据实际遇到的渐消现象，对IQ失衡的时变特性进行了建模。雷达回波的数字信号处理步骤包括脉冲压缩、杂波抑制滤波和CFAR检测，本文拟通过设计脉冲压缩滤波器，在不增加额外计算量的条件下，克服了IQ失衡对后续杂波抑制滤波和CFAR检测的影响。

1.1 面向数字阵列雷达的IQ失衡回波的建模

雷达系统在某些复杂工作模式下由于实际器件的非理想性，导致了I/Q的理想正交无法实现。雷达回波的在某些阶段可能出现IQ幅度和相位的失衡。线性调频雷达信号的理想信号模型为

(1)

定义ωc为即时频率，则IQ信号可表示为

SQ(t)=-sin(ωct)
SI(t)=cos(ωct)

(2)

IQ失衡可以建模为对称形式或不对称形式。在对称形式中,每个支路有一半的相位和幅度误差。在非对称的方法中,I路被建模为理想的,误差在Q路中建模。两种方法其实是等效的，实际接收到的IQ信号存在失衡，可建模为

SRQ(t)=g(t)sin(ωct+φ(t)+φ0)
SRI(t)=cos(ωct)

(3)

其中g(t)是IQ幅度失衡在两路上的比值，这个IQ幅度失衡比值一个随时间变化的量，φ(t)是IQ相位失衡表征量，这个IQ相位失衡量是一个随时间变化的量，φ0是IQ相位失衡初始量。

(4)

在雷达信号接收实际过程中发现，最初的IQ失衡逐渐消减最终趋近于IQ正交。亦即当脉冲内快时间逐渐趋近于脉冲宽度时，IQ幅度失衡比值趋近为-1，而IQ相位失衡从初始相位逐渐变到0。

SR(t)=SRQ(t)+SRI(t)=l1·SQ(t)+l2·SI(t)

(5)

单个子阵接收的IQ不平衡表达式如式(5)所示，其中I和Q的失衡系数分别是l1和l2，其表达式为

l1=gRe-j(φ(t)+φ0)
l2=1

(6)

实际系统的若干个子阵IQ回波经过了DBF合成，合成后的回波YΣ表示为

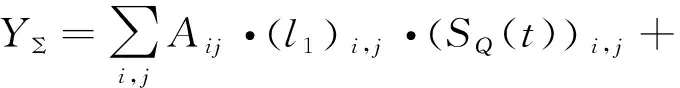
(7)

其中Aij为第i行第j列子阵对应的合成系数，(l1)i,j和(l2)i,j分别为第i行第j列子阵对应的失衡系数。合成后的回波的实部为YrΣ和YiΣ。

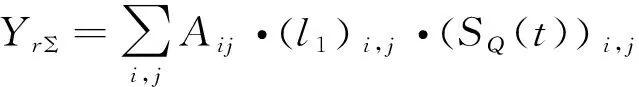
(8)

(9)

其中(l1)i,j和(l2)i,j是固定的，在某些应用场合，通过机扫调整指向，指向改变过程中没有相扫，只是有固定指向的多波束，也就是当DBF波束指向固定下来后Aij是固定时不变的。因此DBF合成后的IQ失衡只是改变了失衡系数，新的IQ失衡系数为Ak1和Ak2。

1.2 面向雷达的IQ失衡回波的适配滤波器设计

一般情况下，回波信号与滤波器做卷积运算实现脉冲压缩。匹配滤波器是信号的共轭镜像，但在IQ失衡的情况下会产生多个类似栅瓣峰值，因此需要设计适配滤波器，该滤波器以主瓣最大化和主瓣外最小化为准则。通过优化求解步骤，实现适配滤波器设计，滤波器设计过程包括构造目标函数和构造等式和不等式约束条件两个主要步骤。

S=[s1,s2,s3,...,sN]

(10)

其中S是采样后的IQ回波信号离散取值序列。

H=[h1,h2,h3,...,hN]T

(11)

其中H为IQ不平衡适配滤波器。

(12)

其中A是等式约束的系数矩阵，在匹配峰值处施加等式约束

S·H=1

(13)

如果要求适配滤波器卷积结果除了主峰以外，其他卷积结果值都一致且足够小则可令

D=A·H=[δ1,δ2,δ3,...,δN]T

(14)

其中A第i行与系数矩阵相乘得Di

Di=Ai·H=[δi]T

(15)

依次对Di求平方得到DBi

DBi=DiTDi=(Ai·H)T(Ai·H)=[δi2]

(16)

对其中的DBi施加不等式约束得到式(17)

DBi<δ2

(17)

式(17)等价于式(18)

δ1≤δ
δ2≤δ
...
δN≤δ

(18)

优化的目标函数为

minδ

(19)

根据适配滤波器设计目标，通过求解二阶锥优化方法，抑制雷达回波信号中IQ失衡带来的影响。

2 仿真研究

仿真条件：工作频点500 MHz；信号带宽100 kHz；信号脉宽1 ms；采样频率125 kHz；IQ不平衡初相π/2+0.2rad；IQ不平衡初始幅度0.23。

仿真过程中，将IQ不平衡相位差建模为渐消过程，随着脉冲内时间的演进，IQ相位不平衡从初相渐消为0，幅度不平衡从初始IQ幅度比渐消为IQ比例为1。

IQ不平衡的幅度差异如图1(a)所示，中部深色曲线表示的是Q路信号，而上下较浅稀疏曲线表示的是I路信号，对比可以看出仿真的原始IQ信号符合模型设计，如果使用标准的匹配函数对IQ失衡信号进行匹配滤波，其结果必然不佳；如果采用IQ信号作自相关，结果如图1(b)所示，会在峰值两侧出现显著而对称的“旁瓣”，在实际检测过程之后，这些“旁瓣”会产生虚警，严重干扰正常目标的探测，这反映了IQ失衡信号对雷达目标探测的影响。为了减少影响，通过优化滤波器可实现对这些“旁瓣”的抑制，IQ失衡信号通过本文提出的滤波器结果如图1(c)所示，旁瓣上的噪底也被很大程度降低了，如此滤波结果有利于旁瓣上可能存在的小目标检测，相邻目标彼此不会相互影响。逆转滤波器的顺序后，将IQ 失衡信号通过逆转后的滤波器，结果如图1(d)所示，从图中可以看出滤波结果不甚理想，多处出现了显著的“旁瓣”，主瓣位置发生改变，且主瓣幅度被大大削弱，这说明了IQ失衡滤波器匹配特性，一方面是由于信号具有调频斜率，另一方面是由于IQ失衡的渐消过程。

不改变滤波器系数，将IQ不平衡回波信号初相偏离原回波信号初相达到π/12时，如图2(a)所示，经过滤波器后的结果没有引入旁瓣峰值，不断增加IQ不平衡信号的初相偏离原信号的初相，仍然没有引入的旁瓣峰值，新信号初相偏离原信号达到π时，仍然没有引入任何的旁瓣峰值。初相偏离无法通过数字收发与信号处理的调整，采样误差在相位级完全可能存在。通过以上仿真表明：本文设计的滤波器，可以克服常见测量中新信号初相偏离原信号初始相位误差，对初始相位误差具有一定鲁棒性。

图1 IQ不平衡回波信号及其经过脉压滤波器的仿真结果

速度失配达到5 m/s时，引入的单侧旁瓣峰值可以忽略不计，随着速度的不断增加，引入的单侧旁瓣峰值也有所增加，当速度误差达到20 m/s时，引入的单侧旁瓣峰值也在5 dB左右，远远小于优化前的15 dB左右的两侧旁瓣峰值。速度可以通过数据处理与信号处理的闭环Kalman滤波减少速度测量误差，经过闭环跟踪后速度测量误差一般都能在10 m/s以下。通过以上仿真表明：本文设计的滤波器，可以克服常见测量中的速度误差，对速度误差具有一定鲁棒性。

3 结束语

IQ不平衡在雷达中会导致目标位置测量偏差、严重的虚警和信噪比下降等严重后果，本文拟通过滤波设计方法解决雷达回波IQ失衡问题。首先面向数字阵列雷达的 IQ失衡回波进行建模，然后设计适配滤波器，该滤波器以主瓣最大化和主瓣外最小化为准则。将滤波器设计问题转化为最优化问题，回波信号与滤波器做卷积运算实现脉冲压缩。并通过设计的滤波器抑制IQ失衡产生的旁瓣峰值，仿真表明：本文设计的滤波器，实现了对称的“旁瓣”抑制，降低了旁瓣上的噪底约4 dB，滤波结果有利于旁瓣上的小目标检测，可使相邻目标彼此不会相互影响。能够克服常见测量中新信号初相偏离原信号初始相位误差，对初始不平衡相位完全不影响滤波结果，同时还可克服常见测量中的速度误差，当目标速度误差达20 m/s时，引入的单侧旁瓣峰值不超过5 dB。采用滤波方法不增加硬件设备，不需要增加额外的工作模式，计算耗费小，在实际雷达工作中具有很强的工程适用性。

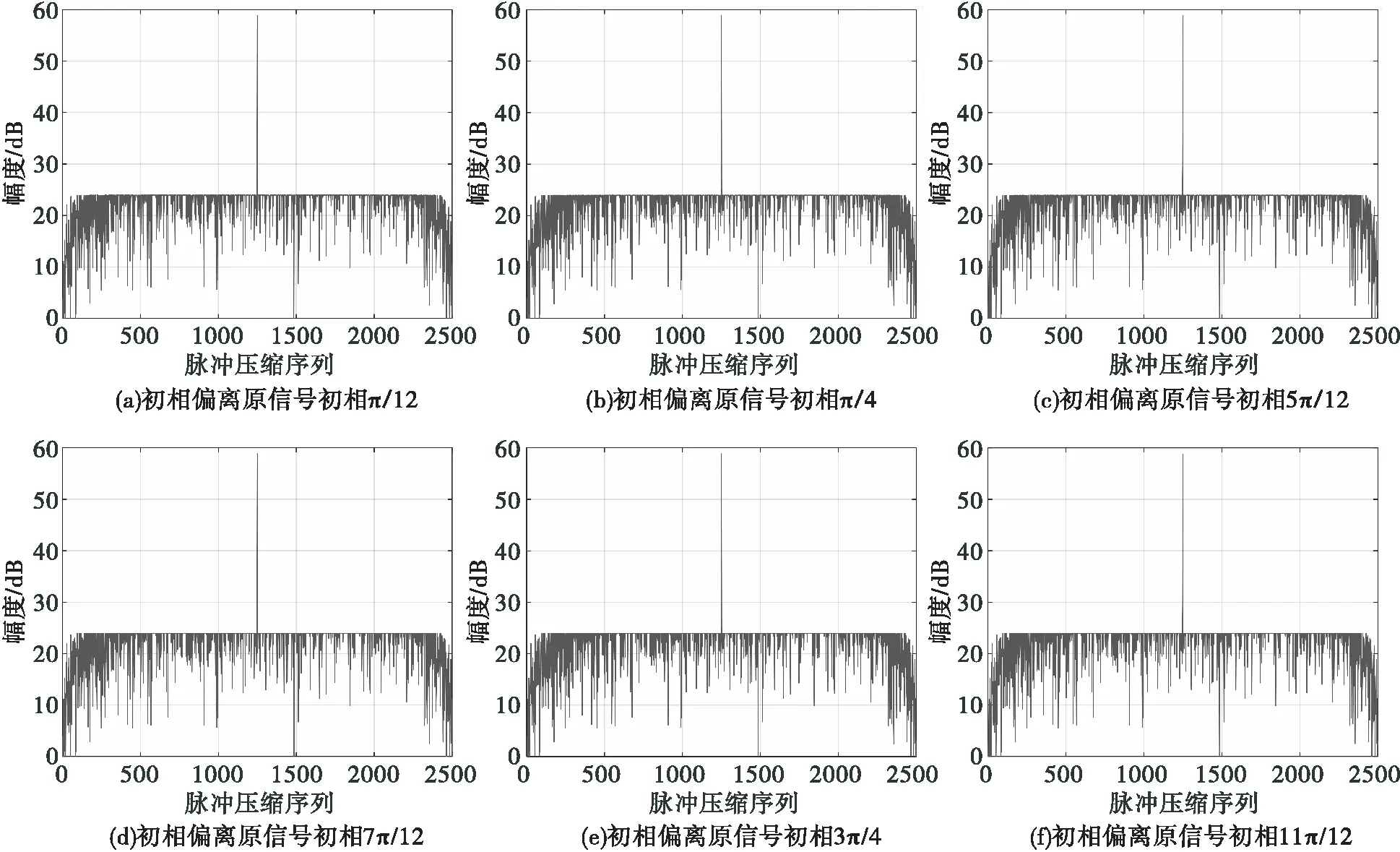
图2 初始相位不同的IQ不平衡回波信号经过同一个优化后脉压滤波器的仿真结果

图3 不同速度 IQ不平衡回波信号经过同一个优化后脉压滤波器的仿真结果