大型公共建筑工程质量保险纯费率厘定研究——基于GLM 及GAM 的实证比较分析

盛金喜，李慧民，段品生，郭海东

（西安建筑科技大学 土木工程学院，陕西 西安710055）

大型公共建筑作为城市商业、文化、体育等公共活动的重要载体，一旦发生较大的工程质量事故，则会造成人员伤亡、经济损失和严重的社会影响。如2007 年山西省某客运站坍塌事故和2018 年江苏省某广场建筑停车场坍塌事故。国外工程质量保险的经济关系与约束机制是落实责任、加强监管、确保质量缺陷高效解决的重要途径[1]。目前我国工程质量保险仍处于试点探索阶段，虽然在北京、上海、深圳等地已出台具体实施办法，但尚未取得良好的实施效果。究其原因在于现行法律环境尚不完善、产品设计存在漏洞，工程质量保险纯费率的厘定未能很好地结合工程实际，缺乏科学性与针对性[2-3]。因此，为有效提升大型公共建筑的工程质量水平，在工程特征的基础上，进行工程质量保险纯费率的厘定尤为必要。

工程质量保险纯费率厘定的相关研究主要围绕费率因子与厘定模型展开。在确定费率因子方面，JOSEPHSON 等[4]通过对2 879 个建筑质量缺陷的整理和分析，从设计、管理及材料等方面总结了影响公共建筑质量的五方面原因；CHAN 等[5]、傅鸿源等[6]在此基础上提出项目自身特征对建筑质量的重要影响，进一步完善了费率因子体系；梁健娟[7]从宏观视角分析了开发商、勘察设计单位、承包单位以及监理单位对工程质量的影响；LEE 等[8]利用社会网络分析方法研究施工新技术对工程质量的影响。然而，现有关于工程质量保险费率因子的研究多侧重于住宅，鲜有针对大型公共建筑的，与工程实际的结合亦不充分。

在纯费率厘定模型方面，主要包括经验费率法和频率-强度法两类。在经验费率法方面，赵秀影等[9]结合我国工程质量风险管理模型，基于经验统计方法建立了“分类费率+增减费率”的厘定流程；赵金先等[10]通过分析房屋工程质量潜在缺陷影响因素，得到质量保险经验纯费率修正系数。该方法因计算简便而得到广泛应用，较适合成熟险种的纯费率厘定。在频率-强度法方面，赵海鹏[11]通过比较房屋质量保险理论及国内外保险制度模型，在我国首次建立了房屋质量保险纯费率精算模型，并利用简单随机分布拟合损失数据计算保险纯费率；FU等[12]、FREES 等[13]、孟 生 旺[14]等 则 用Poisson 分 布 和Gamma 分布拟合损失频率和损失强度数据，从纯技术角度分析并计算纯费率的合理性。该方法具有准确度高、针对性强等特点，适合新险种的费率厘定，CHEN 等[15]对特大洪灾保险进行了定价研究并取得了一定成果。由于大型公共建筑工程质量保险仍处于探索阶段，因此，本文选择频率-强度法作为工程质量保险纯费率厘定方法。

为更准确地厘定大型公共建筑工程质量的保险纯费率，首先，通过文献分析总结影响大型公共建筑工程质量的因素，并在此基础上提炼相应的费率因子；然后，在频率-强度法基础上，提出以广义线性模型（generalized linear models，GLM）和广义可加模型（generalized additive models，GAM）预测纯保费；最后，用工程数据对不同分布假设下建立的模型进行实证分析，选出最优模型，以期为大型公共建筑工程质量保险制度的实施提供关键技术支撑。

1 工程质量保险费率因子

工程质量保险费率因子是指显著影响工程质量的因素集合，是进行保险纯费率厘定的基础和关键。通过文献分析及调研，得到影响大型公共建筑工程质量的因素，见表1。

1.1 项目负责人工作经验F1

项目负责人工作经验亦称项目经理能力[22]，是指项目负责人从事工程项目的年限。工作经验丰富的项目负责人，专业技能相对较强，质量意识较高，并具有较好的项目协调能力。

表1 大型公共建筑工程质量问题损失影响因素汇总Table 1 Factors of the large-scale public building quality insurance pure premium rate making

1.2 项目承包单位资质F2

项目承包单位资质亦称项目参与各方资质水平[18]、项目管理水平[20]等，体现承包单位对项目的综合管控能力，也是实现建筑项目从无到有的主体，承包单位资质与工程质量密切相关。根据住建部《建筑业企业资质标准》（建市[2014]159 号），承包单位资质包括特级、一级、二级及三级。不同资质的承包单位，其在资金管理、协作水平、施工人员素质、施工规范、施工机械等方面存在差距，这些均会对大型公共建筑工程质量产生巨大影响。通常承包单位资质越高，项目出现质量问题的概率越小。

1.3 建筑使用性质F3

建筑使用性质亦称工程项目类别[19]、建筑性质[21]等，是大型公共建筑公共服务属性的根本体现。根据《民用建筑设计通则》（GB50352—2005），建筑使用性质包括商业建筑、办公建筑、旅游建筑、通信建筑、交通建筑、体育建筑、教育建筑等。使用性质不同，其建筑形式、建造方式、功能要求、设计服务人数、高峰使用人数等也不同，且差异较大，因工程质量问题造成的损失差别也较大。

1.4 地理区位F4

地理区位亦称项目所在地地质条件[22]、天气条件[23]等，指该建筑所处的区域地理状况。根据《建筑气候区划标准》（GB 50178—1993），大型公共建筑地理区位分Ⅰ级～Ⅶ级。地理区位直接影响建筑的功能与使用，尤其影响建筑使用阶段质量问题的类型、频率及强度。

1.5 建筑结构形式F5

建筑结构形式亦称项目结构特征[19]。由于主要材料、施工工艺、养护技术差别较大，建筑结构形式不同，发生的质量问题亦各不相同。根据《建筑抗震设计规范》（GB 50011—2010），大型公共建筑常用的结构形式有混凝土结构、型钢混凝土结构、钢结构和其他结构4 类。混凝土结构的主要质量问题为混凝土浇筑缺陷；型钢混凝土结构在大型公共建筑中使用较多，其主要质量问题与混凝土结构类似；钢结构的主要质量问题为锈蚀等，损失频率与后期维护情况密切相关；其他结构，如砖混结构和砖木结构，很少用于大型公共建筑，因此，质量问题占比较小。

1.6 项目工期F6

项目工期亦称时间管理[22]、进度控制[23]等。合理的项目工期是保证建筑工程质量的重要前提。项目工期对工程质量的影响主要体现在两个方面。一方面，合理的工期使得施工技术得以在正常条件下顺利开展，并为施工技术、作业环境与作业人员之间的不匹配性提供了适当的可接受空间。另一方面，合理的工期能够使作业人员保持良好的工作状态，高效完成工作，避免因工期过紧放松对质量的把控。

1.7 总建筑面积F7

总建筑面积亦称建设规模[19]。总建筑面积一定程度上体现的是建筑工程的综合性和施工难度。随着总建筑面积的增大，对建造技术和施工管理的要求也随之提高，同时，大型公共建筑的使用功能具有特殊性、复杂性和集成性等特点，如何确保工程质量也是对建筑工程各相关主体的挑战。

1.8 工程总投资F8

工程总投资亦称项目总造价[5]，是指为完成该项目投入资金的总额。在原建设部制定的《注册建造师执业工程规模标准》中，大型房建公共工程的单项建安合同额一般需在1 亿元以上，工程总投资越大，项目受公众关注的程度越高，对工程质量的把控也更严格，资金运用也更宽松，因工程质量导致的损失频率及强度亦较低。

1.9 质量问题类型F9

质量问题类型亦称结构腐蚀[21]、预期质量水平[23]等。不同类型的质量问题导致的损失差距较大。总体看，建筑质量问题有构件类问题和功能性问题。构件类问题主要包括建筑承重结构问题及围护结构问题等，如：主体结构混凝土缺陷、室内地面下陷等；功能性问题指影响建筑正常使用功能的各类问题，包括保温层破坏、室外地坪塌陷等。根据这两类问题的特点及大型公共建筑质量保险发展实际，本文将质量问题类型分为承重结构质量问题、非承重结构质量问题、外部质量问题、附属设施质量问题4 种。

1.10 项目新技术数量F10

项目新技术数量亦称新技术掌握程度[17]、项目复杂程度[23]等。大型公共建筑常作为区域代表性建筑，因外形独特、结构复杂、功能特殊，项目施工中需采取新技术。对于大型公共建筑施工新技术的认定可依据住建部《建筑业10 项新技术》（2017 版）。虽然新技术在使用前经过反复试验，但在大型公共建筑工程施工过程中，可能因缺乏操作经验，使得建筑工程存在潜在的隐蔽缺陷，这些隐蔽缺陷将随使用年限的临近逐渐暴露。

1.11 保险免赔额F11

建筑工程质量问题的保险免赔额由保险人和投保人事先约定，损失额在约定数额或约定比例内的，由投保人自行承担。在保险期内，若被保项目发生质量问题的损失未超出设定的免赔额，则被保项目的损失金额为零。据计算，若损失金额大于免赔额的某点概率为p，则该点的损失概率为不设置免赔额的1/(1-p)倍。

现有研究普遍认为工程质量保险费率因子的确定应遵循公平合理、相互独立、便于计算的原则[18]。为此，本文基于大型公共建筑工程质量问题损失影响因素和费率因子确定原则，对保险费率因子进行提炼，结果见表2。此结果得到土建专家和金融专家的认可，认为所确定的费率因子体系能综合表征大型公共建筑质量问题的损失程度，符合实际，且易于操作。

表2 影响因素-保险费率因子对照Table 2 Comparison of influencing factors & rate factors

2 工程质量保险纯费率厘定理论基础

频率-强度法通过历史数据建模计算损失频率及损失强度的预测值，将两者乘积作为纯保费预测值，进而计算保险费率[25]。根据KOZLOWSKI 在2008 年非寿险精算师协会研讨会上的观点，由于工程环境的多变性，用频率-强度法厘定费率更便于对结果的监控。GLM 已被广泛应用于频率-强度法，因其综合考虑了影响工程质量的各因素，厘定的费率更科学。GAM 提高了处理连续型变量的能力，是对GLM 的完善和补充。

本文基于频率-强度法，以GLM 和GAM 为基础进行大型公共建筑工程质量保险费率厘定模型的构建与优选。

2.1 GLM、GAM 的基础理论

2. 1.1 GLM 的基础理论

GLM 是线性模型的推广，也是目前国内各大保险公司广泛应用的一种保险精算模型。该模型主要通过将函数因变量的表示由传统的正态分布转换为指数分布族，并通过引入连接函数，将因变量的均值以函数变换的方式表示为参数的线性组合，见式（1）。指数分布族的基本形式见式（2），在GLM 中，函数的均值及方差可分别用b′(θ)和(θ)表示。

其中，μ为被解释变量的期望，Y 为服从指数型分布的被解释变量，X 为解释变量，β 为待估回归参数向量，ε 为随机误差向量，g(μ)为已知的严格单调且光滑的函数，称连接函数。

其中，θ为自然参数，与分布均值有关；φ为离散参数，与分布方差有关；ω为先验权重，来自样本观察值；b(θ)为二阶可导且二阶导数为正的已知函数；c(y,φ)已知,为与参数无关的函数。

模型可采用极大似然估计法估计回归参数β，若为饱和模型参数估计值（饱和模型是准确预测被解释变量的模型），其极大似然函数为)，模型参数个数为n为回归参数估计值，极大似然函数为，模型参数个数为k。定义尺度化偏差（scaled deviance,SD）为SD=2[l(max)-l)]，如模型预测效果好，则SD 服从自由度为n-k的卡方分布，通过假设检验模型的显著性[7]。

2.1.2 GAM 的基础理论

由于GLM 未考虑变量的非线性影响，而影响工程质量的因素与损失程度之间可能存在强烈的非线性关系。与GLM 类似，GAM 是可加模型的推广，通过在模型中添加非参数项来体现非线性影响并计算模型的参数估计值。

GAM 主要由随机部分、系统部分及连接部分组成。其中，随机部分，解释被解释变量Y，各观察值相互独立且服从如式（2）所示的指数分布族。系统部分，用解释变量的线性组合预测被解释变量，在GAM 中，该线性组合为参数部分和半参数部分的可加形式，如式（3）所示。

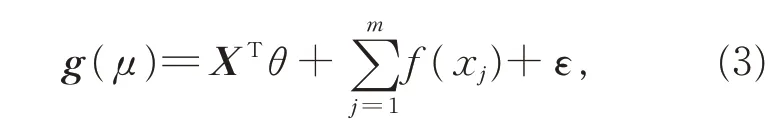
其中，前半部分是部分解释变量的线性组合，为参数部分；后半部分是其他解释变量经函数变换后的线性组合，为半参数部分。函数f（·）为半参数解释变量的光滑函数，可选择局部多项回归函数、光滑样条函数、B 样条函数等作为光滑函数。连接部分，通过一个严格单调且充分光滑的函数将系统部分和随机部分经恒等连接、对数连接等方式相连接。

GAM 中的光滑函数有多种选择，在R 软件的mgcv 包中，GAM（）默认选择的是薄板样条函数。可通过惩罚最小二乘法或惩罚极大似然法求解样条：

其中，等式右边第1 项为估计值与观察值之间的拟合优度，第2 项为粗糙罚的约束，λ为光滑参数，控制罚的程度，λ越大，第2 项的比重越大，函数拟合曲线越平滑；否则越粗糙[14]。

2.2 GLM、GAM 比较优选方法

GLM、GAM 比较优选方法主要用于选择最优分布假设并判断分布假设是否合理，有赤池信息准则（Akaike information criterion，AIC）、贝叶斯信息准则（Bayesian information criterion，BIC）等，其中AIC 因计算简便被广泛使用，其计算式为

其中，l为模型的对数似然函数，k为模型的参数个数。AIC 值越小，表示质量问题损失模型的拟合效果越好[14]。

3 实证分析

3.1 数据描述

选取无锡苏宁广场、中国博览会会展综合体等46 栋竣工于1993—2016 年的大型公共建筑并对其基础数据进行分析，46 栋建筑的分布城市见表3，数据主要来源于重大工程案例研究和数据中心（http://www.mpcsc.org）、住建部《建筑业10 项新技术（2017 版）》以及大型公共建筑保险试行情况汇总，该数据集不包括项目负责人工作经验（F1）和保险免赔额（F11）数据。

表3 46 栋建筑的城市分布Table 3 The urban distribution of 46 buildings

从建筑性质看，主要包括办公建筑、交通建筑以及体育建筑3 种类型，占比分别为65%，31% 和4%；这些建筑大多位于上海、广州等一、二线城市，地理区位主要处在Ⅱ级、Ⅲ级和Ⅳ级，占比分别为44%，28%和28%；承包单位资质主要为施工总承包特级资质和一级资质，占比分别为93%和7%；结构形式主要为型钢混凝土结构、混凝土结构及钢结构3 种，占比分别为43%，43%和14%；质量问题主要包括承重结构质量问题、非承重质量问题、外部质量问题3 种，占比分别为22%，43%和35%；项目工期、总建筑面积、工程总投资和新技术数量为连续型变量，这4 个变量与损失频率、损失强度之间的关系如图1 所示。

3.2 纯费率厘定模型构建

分别以损失频率及损失强度为被解释变量，建立各分布假设下的GLM 及GAM。根据工程质量问题损失分布的一般特征，损失频率为非负计次型变量，通常服从Poisson 分布、Negative Binomial 分布，分别在这2 种分布假设下建立GLM 和GAM，计算保险损失频率；损失强度为连续型变量，通常服从Gamma 分布、Inverse Gauss 分布，分别在这 两 种 分布假设下建立GLM 和GAM，计算保险损失强度。以上分布假设均属指数分布族，建立以下8 个模型。

图1 部分解释变量损失情况变化曲线Fig.1 Loss situation change curves of some explains variables

模型1以损失频率为被解释变量，假设Y 服从Poisson 分布，建立对数连接函数下的GLM：

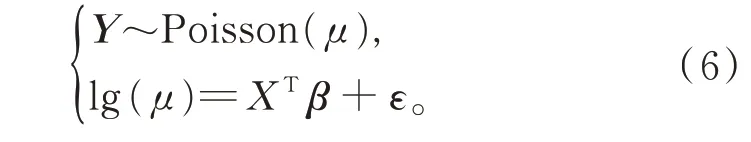
模型2以损失频率为被解释变量，假设Y 服从Negative Binomial 分布，建立对数连接函数下的GLM：

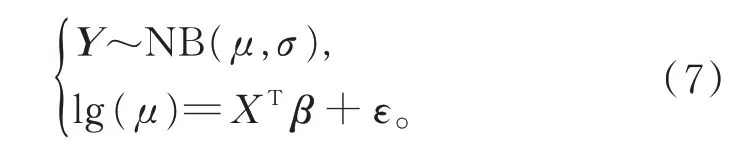
模型3在模型1 基础上，考虑变量的非线性影响，以损失频率为被解释变量，假设Y 服从Poisson分布，建立对数连接函数下的GAM：

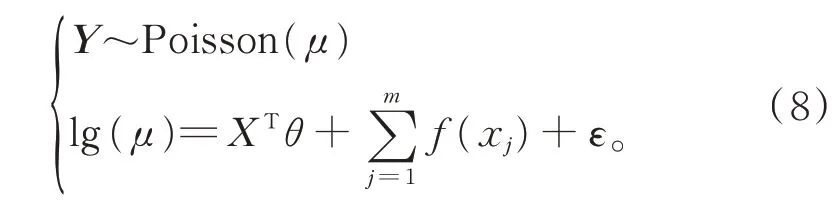
模型4在模型2 基础上，考虑变量的非线性影响，以损失频率为被解释变量，假设Y服从Negative Binomial 分布，建立对数连接函数下的GAM：

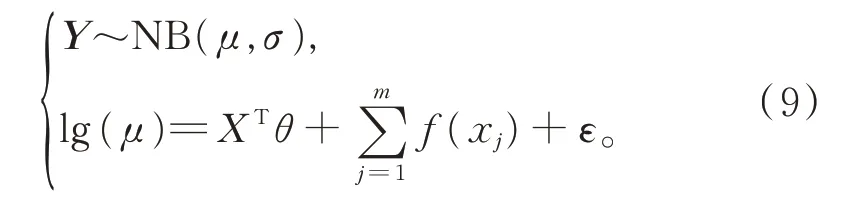
模型5以损失强度为被解释变量，假设Y 服从Gamma 分布，建立对数连接函数下的GLM：

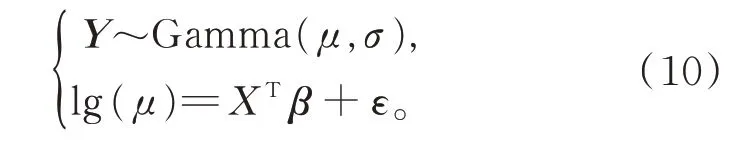
模型6以损失强度为被解释变量，假设Y 服从Inverse Gauss 分布，建立对数连接函数下的

GLM：

模型7在模型5 基础上，考虑变量的非线性影响，以损失强度为被解释变量，假设Y服从Gamma分布，建立对数连接函数下的GAM：

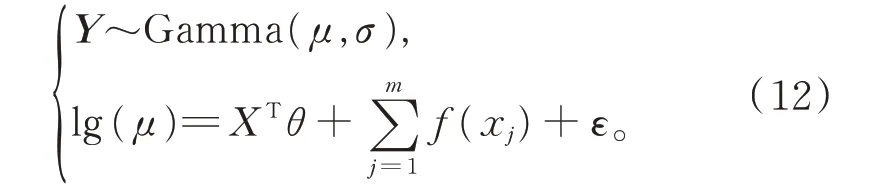
模型8在模型6 基础上，考虑变量的非线性影响，以损失强度为被解释变量，假设Y 服从Inverse Gauss 分布，建立对数连接函数下的GAM：

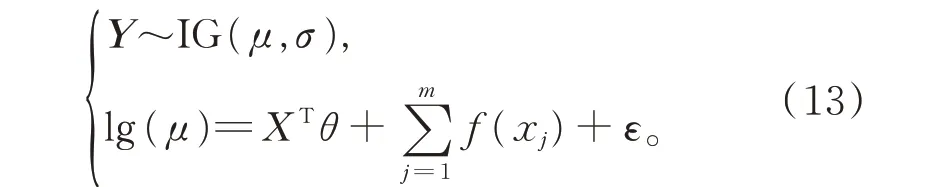
3.3 计算结果分析

根据构建的大型公共建筑工程质量保险纯费率厘定模型，分别计算模型期望值，得到工程质量保险损失频率及损失强度预测值。为避免变量之间出现完全共线性现象，将各费率因子中出现次数最多的因子作为基础变量，即将承包单位特级资质、建筑使用性质为办公建筑、地理区位为Ⅱ区、结构类型为型钢混凝土结构、外部质量问题等作为基础变量。在此基础上，结合图3，首先将所有解释变量作为参数建立GLM，然后将项目工期、总建筑面积、工程总投资及新技术数量作为非参数，其他部分作为参数建立GAM，计算模型的AIC，选择最优模型。在GAM 中，通过AIC 判断并选择光滑函数节点数，最终得到当样条节点数为7 时模型的拟合效果最好， 模型参数估计结果见表4。

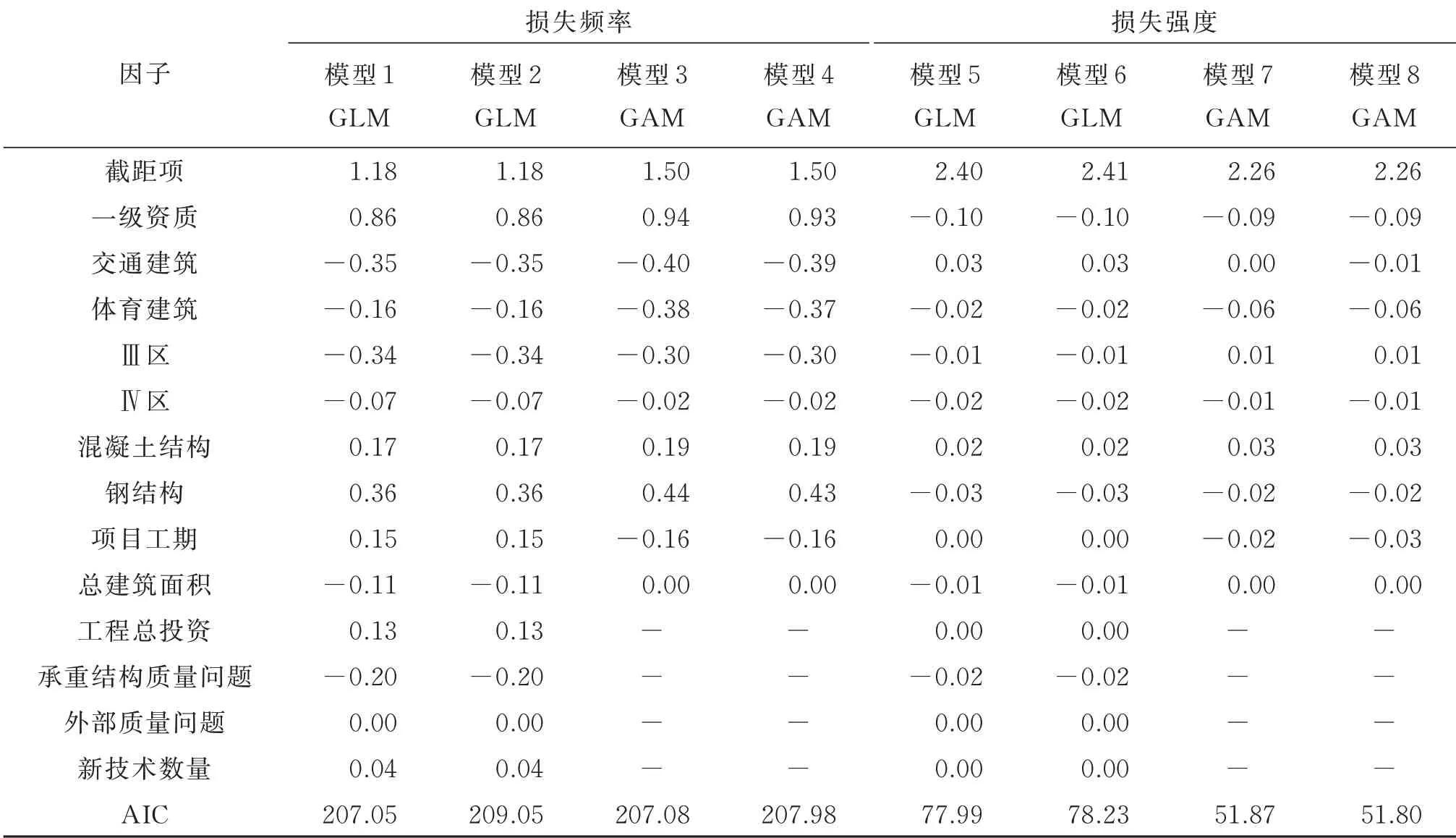
表4 GLM 及GAM 的参数估计结果Table 4 Parameter estimation results of GLM and GAM

由表4 可知，从损失频率看，GLM 略优于GAM，模型采用的假设为Poisson 分布和Negative Binomial 分布，而Poisson 分布的拟合效果优于Negative Binomial 分布，效果最好的为模型1；从损失强度看，GAM 略优于GLM，模型采用的假设为Gamma 分布和Inverse Gauss 分布，而Inverse Gauss分布的拟合效果优于Gamma 分布，效果最好的为模型8。表5 为模型8 GAM 的非参数估计结果，说明所选择的非参数项适合该数据集，但新技术数量估计的自由度为1，表示该指标可能为参数项。

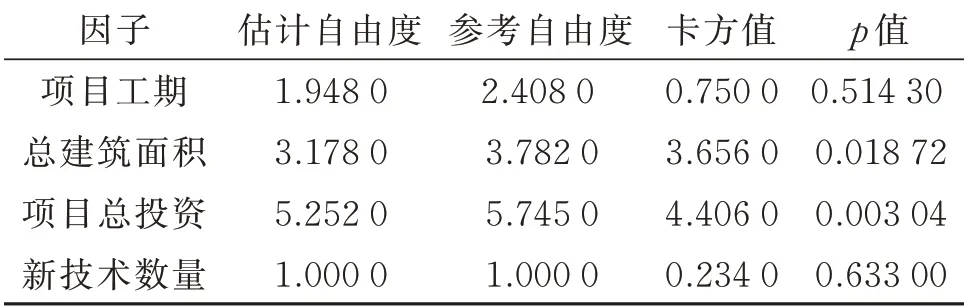
表5 模型8 GAM 的非参数估计结果Table 5 Non-parametric estimation results of GAM in model 8

模型1 和模型8 的QQ 图分别见图2 和图3，从此两图看，散点分布近似为一条直线，可以判断残差符合正态分布，模型1 Shapiro-Wilk 检验的p值为0.519 5，模型8 Shapiro-Wilk 检验的p值为0.775 8，均大于0.05，可拒绝原假设，即2 个模型的残差符合正态分布，使用的分布假设合理。

综上所述，GLM 和GAM 拟合效果较好，可用于大型公共建筑工程质量保险纯费率的厘定，所选分布假设合理可行。

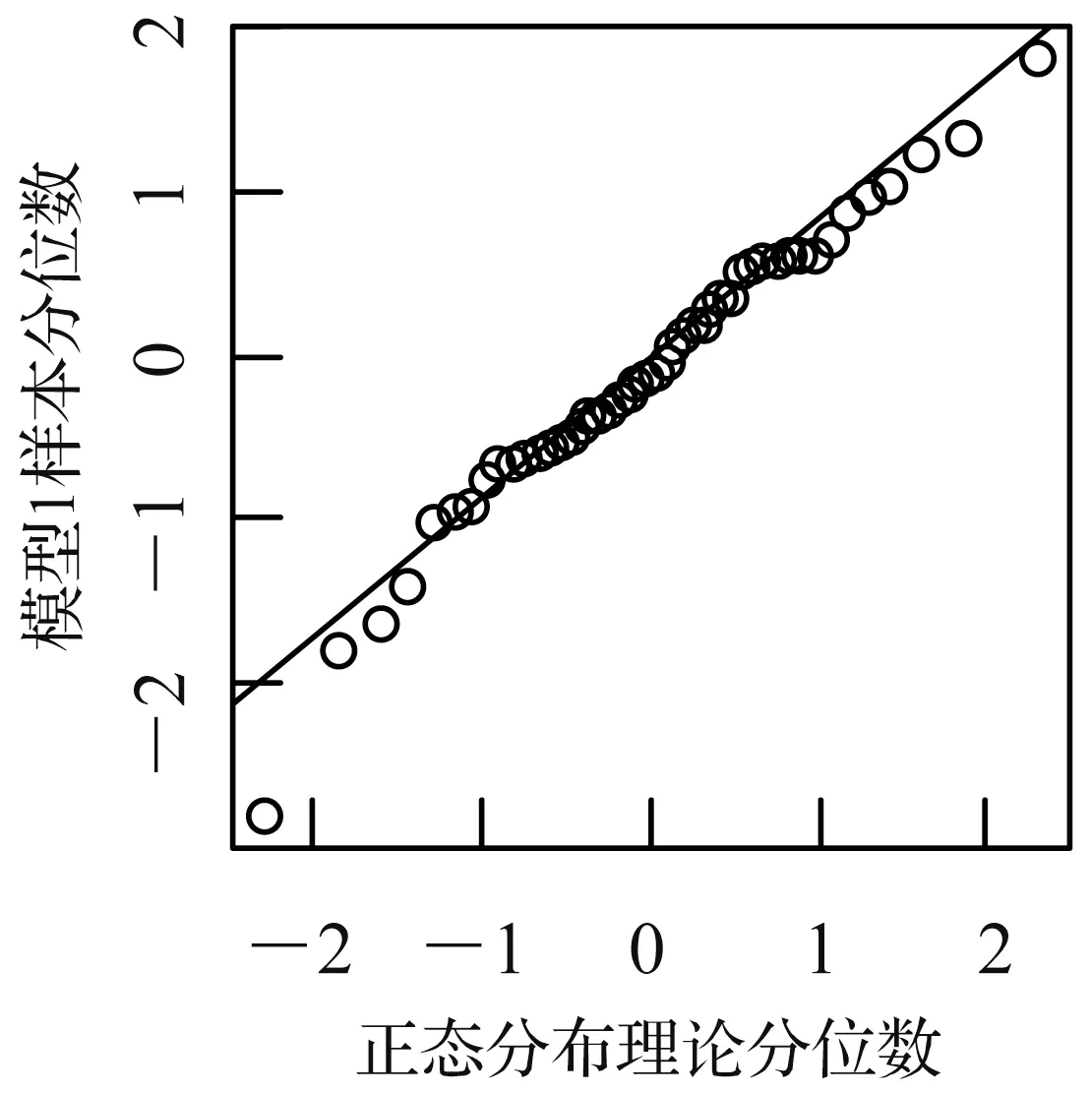
图2 模型1 的QQ 图Fig.2 QQ diagram of model 1

最后，对保险费率进行计算。损失频率计算选择模型1，损失强度计算选择模型8。从某保险公司对我国大型公共建筑的保险试行状况看，利用该模型计算的保险纯费率合理可行。需要说明的是，正式保险费率中还应包含附加费率，因附加费率涉及公司商业机密，需根据公司具体情况进行适当调整。

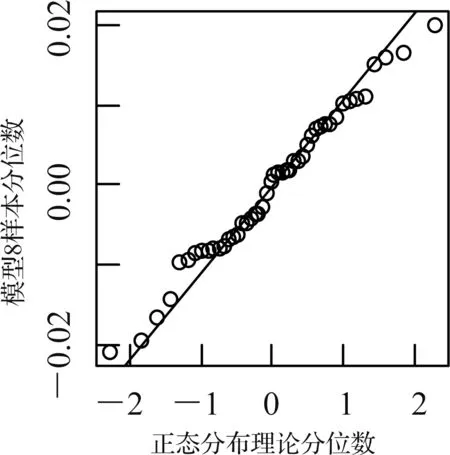
图3 模型8 的QQ 图Fig.3 QQ diagram of model 8

4 结 论

在分析我国大型公共建筑建设规模和国内外建筑质量保险纯费率厘定研究现状的基础上，从大型公共建筑工程质量问题损失的影响因素出发，结合费率因子确定原则，提炼了11 项保险费率因子。

基于频率-强度法思想，提出在Poisson 分布、Negative Binomial 分布、Gamma 分布、Inverse Gauss分布的假设下用GLM 和GAM 分别建立保险纯费率厘定模型，并通过计算AIC，得到优选模型。用我国竣工于1993—2016 年的46 栋大型公共建筑的基础数据对模型进行了合理性验证，得到模型的拟合效果较好，GLM 和GAM 可用于大型公共建筑保险纯费率厘定。

由于保险行业的特殊性，难以获取足够数量的大型公共建筑保费数据。后续研究可通过增加样本数量，进一步提高模型的拟合精度，并针对不同类型的大型公共建筑工程质量厘定对应的保险费率；完善大型公共建筑工程质量保险费率厘定因子体系，研究损失频率与损失强度相关情况下的工程质量保险费率厘定；探索采用其他非寿险精算模型厘定纯费率（如广义线性混合模型、分层广义线性模型等），也可在大数据背景下采用机器学习方法厘定保险费率。