地下洞体结构断裂特征及时变稳定性研究

李云，刘霁，王军

地下洞体结构断裂特征及时变稳定性研究

李云1，刘霁1，王军2

(1. 湖南城建职业技术学院 建筑设备工程系，湖南 湘潭 411101；2. 湖南工程学院 建筑工程学院，湖南 湘潭 411101)

针对复杂条件下窑体结构的裂纹分布和变形特征，通过垂直优势节理裂隙黄土体的断裂力学特性，分析翼形裂纹的扩展趋势，建立靠崖窑优势垂直节理裂隙土体的翼形裂纹和共线裂纹模型，得出翼形裂纹折算长度的计算式和应力强度因子的计算式，推导出含洞室共线裂纹的应力强度因子计算式。同时还得到Burgers蠕变模型的位移表达式和锚固荷载的计算式。通过算例研究表明：建立的断裂和蠕变模型，反映了窑体结构的位移和塑性区分布及时效稳定性特征。研究结果可为窑体结构的加固设计提供有益参考。

地下窑体结构；断裂特征；蠕变模型；加固与稳定性

窑洞作为典型的生土建筑和节能建筑[1−2]，在我国陕西、甘肃、宁夏、山西、河南和河北等地区广泛分布。国内对生土建筑的研究主要集中在生土建筑的结构与构造、窑室布局和表现等方面[3]，并且其研究文献资料也不多，且大部分都偏重于窑洞建筑形态方面，在窑洞的布局、整体规划、空间处理、几何构造等进行了研究，取得了一些成果，如童丽萍等[4]根据黄土层的分布情况，对黄土窑洞的构造参数，选址方面进行了研究,指出黄土材料是最理想的保持生态自然系统中物质流与能量流平衡的材料；卫峰等[5]通过现场调查土窑洞受震害的实例，分析了土窑洞的震害特征及破坏机制，提出了土窑洞的抗震构造措施；陈国兴等[6]通过对崖坡地震稳定性的拟静力分析，得出了崖坡的临界高度和黄土崖窑洞的地震破坏判据；吴成基等[7]根据大量黄土窑洞的现场调查，对窑洞坍塌的原因进行了分析，提出了黄土窑洞建造时在高度和坡度方面的技术措施。而对窑洞土体结构的断裂力学特性与位移变形计算、应力塑性区分布和窑洞加固技术及其稳定性时效特征的研究缺乏系统的理论和应用研究，在这方面的研究文献更少。因此利用仅有的研究成果、理论和技术对窑洞土体结构的裂纹分布与演化特征和时效稳定性的研究具有挑战性。为此，笔者根据靠崖窑土体竖向优势节理裂隙的分布特点，结合Irwin塑性区裂隙顶端的张开位移公式，得出了翼形裂纹折算长度的计算式和应力强度因子的计算式，推导出含洞室共线裂纹的应力强度因子计算式。同时还建立了适应靠崖窑土体蠕变变形的非线性黏滞系数的表达式和蠕变方程，综合考虑窑洞土体固有的力学特性并结合数值模拟技术分析靠崖窑的时效稳定性问题，为窑洞工程的加固稳定和适用性设计提供技术支持[8]。

1 窑洞结构性土体断裂力学特性

组成靠崖窑结构的土体主要为黄土，黄土是一种结构性较强的特殊土，具有湿陷性和竖向节理的特点。黄土体断续节理裂隙在荷载作用下的起裂、扩展、成核、贯通和相互作用对窑洞土体结构的力学性能产生显著的影响，它可以导致窑洞土体强度和结构稳定性的逐渐劣化直至最后破坏。关于节理裂隙特点对黄土体强度和土体结构稳定性的影响，国内外的研究文献较少，这主要是因为窑洞体周围由黄土材料构成，其材质不具有单一性、同向性、均质性和连续性，且受空间分布的差异性、结构性、微细观力学特性等复杂因素影响，因此没有被 关注。

1.1 垂直优势节理裂隙黄土体的裂纹模型

窑洞土体复杂应力场对裂隙黄土裂纹的萌生、扩展与否具有重要的影响。文中暂不考虑外界环境的变化，窑洞土体结构受到的主要应力有：洞顶上覆土体的自重、洞顶荷载、侧墙的土压力和沿洞室轴线的土压力，处于三维应力状态。根据线弹性断裂力学中的叠加原理，该三维应力分布可由图1所示的主应力情况叠加而成[9−10]。

图1 复杂应力情况下的加载和叠加

图1中：为主裂纹的半长；为主裂纹与最大主应力面的夹角；为翼形裂纹与主裂纹的夹角；为翼形裂纹的半长；为主应力，且取值为1， 2，3。

根据图1主应力叠加原理中节理裂隙的分布情况，下面从2个方面来研究裂纹扩展和应力强度因子的求解。

1) 不考虑翼形裂纹的扩展

由图1(b)主裂纹尖端的应力强度因子可写成如下形式，在这里以压应力为正，拉应力为负：

由图1(c)主裂纹尖端的应力强度因子可写成：

2) 考虑翼形裂纹的扩展

为便于计算和推导翼形裂纹对主裂纹的应力影响，在这里可以将形成的主裂纹与翼型裂纹合成长为2的直线裂纹，见图2。该直线裂纹是由2段组成：主裂纹长为2，折算的翼形裂纹长度为2eff，2eff是翼形裂纹2,翼形裂纹方位角和主裂纹方位角的函数，等效直裂纹与主裂纹和折算的翼形裂纹的长度关系为：

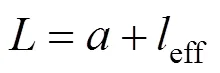
将翼形裂纹投影在主裂纹方向上，就可以得到翼形裂纹的折算长度eff，依据公式(4)，可求得直裂纹的等效长度为：

由式(5)和图2，裂纹尖端的应力强度因子可 写成：

1.2 多组优势共线裂纹模型的分析

黄土体的孔隙性和垂直优势节理裂隙的分布现实已得到工程界的广泛认可，为了研究多组垂直优势共线节理裂隙对靠崖窑土体结构的影响，文中对复杂应力条件下的窑洞模型进行了概化，即窑洞土体主要受到顶部和底部对称荷载和土的侧压力应力作用的影响，不考虑中间应力的影响，其结构尺寸和荷载分布见图3所示。

图3 概化的模型

图中主应力关系为：

图3中等间距的裂纹代表黄土体中多组垂直优势共线节理裂隙，其垂直间距为2，水平向间距为，窑洞顶部的裂纹长度为，竖向优势裂纹长为2，窑洞的半径为，拱顶荷载和上覆土层的自重为，为窑洞侧壁土体侧压力系数，为泊松比。

针对共线裂纹分布的特点，为便于分析计算，将坐标原点放在任一竖向优势裂纹的中点，可以得到满足边界条件的应力函数为[11]：

根据线弹性断裂力学中的叠加原理，可以 得到：

又根据应力强度因子的定义式：

根据共线裂纹的应力因子求解式，可得

同理可以得到其他情况下的应力强度因子计算式：

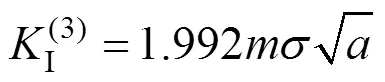
2 窑洞结构蠕变稳定性分析

窑洞的稳定性变化是一个复杂的过程，窑洞土体结构的变形并不是在瞬时完成，而是随着时间的延续其变形也在不断地发展，因此在土体介质强度逐渐发挥的同时，窑洞土体强度和稳定性的研究应该要考虑土体蠕变特性的影响。

2.1 窑洞土体的蠕变变形特性

靠崖窑赋存于土体中，是一种典型的土拱结构，其结构的变形表现为窑洞土体的变形，主要是由窑脸边坡的位移、窑洞周围土体的位移、窑腿的位移和上覆土层的位移，由于土体材料结构特性和固有的力学属性，因此上述变形并不是在瞬时完成，而是具有蠕变时效性[12]。靠崖窑窑洞结构的变形具有含地下洞室土质边坡的特点，其变形过程有相似之处，又依据现场调查与监测数据，窑洞土体的蠕变变形特点主要包括：土体的蠕动变形、挤压变形、滑动开裂变形和破坏的加剧变形阶段。考虑到靠崖窑洞室土体以上变形特点具有瞬时弹性、塑性、稳定的塑性流动、不稳定的塑性流动共存，故总应变量可由瞬时弹性，塑性，稳定的塑性流动，不稳定的塑性流动变形−等4部分组成。

把窑洞土体的变形分成弹性变形和蠕变变形2部分，而且在任何时刻的总变形是这2部分 之和。

在窑室土体非线性蠕变分析中，随着时间的延续，不仅总变形增加，并且弹性变形，黏弹性变形和不可恢复的黏塑性流动也同时增加。

2.2 改进的Burgers非线性蠕变模型

蠕变作为土体材料固有的力学属性已被科学界和工程界所接受，并且在实验、理论和应用方面已取得了重大研究成果[13]。其中Burgers模型具有模型形式简单，模型参数容易获取，能较好地反映土体的弹性、黏弹性、塑性变形特性，也能较好地描述土体蠕变第3期以前的变形特性，即衰减蠕变和稳定蠕变变形，因此该模型已被广泛应用[14]。然而Burgers模型的研究和应用在窑洞土体变形的研究和应用方面的文献资料相当少，同时该模型还不能考虑土体破坏加速变形的过程，即蠕变全过 程[15]。大量研究表明，土体材料变形具有瞬弹、塑性、黏性、黏弹性共存的变形性质，因此依据蠕变模型理论的研究成果，结合广泛适用土体工程的Mohr-Coulomb塑性屈服准则，对蠕变模型是线性蠕变模型Burgers模型进行改进，建立能模拟土体材料黏弹塑性和蠕变全过程的非线性蠕变模型，可以进一步研究靠崖窑土体的黏弹塑性蠕变特性。改进的Burgers非线性模型是由Maxwell模型、黏塑性模型和自添加的非线性塑性元件串联而成，反映的是蠕变的前2个阶段，而非线性特征和土体的加速蠕变阶段主要由Mohr-Coulomb塑性元件来实现，如图4所示。

图4 改进的Burgers蠕变非线性模型

图4中：1为土体的瞬时变形模量；2为黏弹性变形模量；1为土体的黏滞系数；2为黏弹性黏滞系数；σ−C为非线性塑性元件的应力阈值，是窑洞土体出现加速变形破坏力的下限值，在满足该情形下的变形，已显示出靠崖窑土体结构已出现贯通的塑性区。

本研究中塑性屈服准则采用广泛适用于土体的Mohr-Coulomb拉伸破坏和剪切破坏相结合的复合屈服准则[16]，其中Mohr-Coulomb准则的剪切屈服函数为：

3 算例分析

为了分析土体的时变特性对受锚靠崖窑洞结构的蠕变稳定性，文中采用显示差分的FLAC3D程序和自带的FISH开发语言及计算机语言VC++，运用半圆拱窑体结构的实例进行核验。数值计算范围高度为20 m，窑洞进深为6 m，数值计算宽度B为23 m，窑洞结构的其他尺寸见图5所示。锚固力学参数为：锚杆长度为2.5 m，沿窑顶分布，间距为2 m×2 m，锚杆钢筋为φ22HRB335，浆体材料为M15，面层为C20。用差分单元对土体结构数值模型进行界定，共划分为19 837个节点，5 679个四面体单元，锚杆的数值模型共划分为32个cable单元，48个节点。下部位移固定作为力学边界，两侧水平位移和速度固定，上部为自由面边界；其中窑体结构的计算范围和网格划分见图6所示，土体的力学参数和锚杆参数见表1所示，计算结果见图7～9所示。

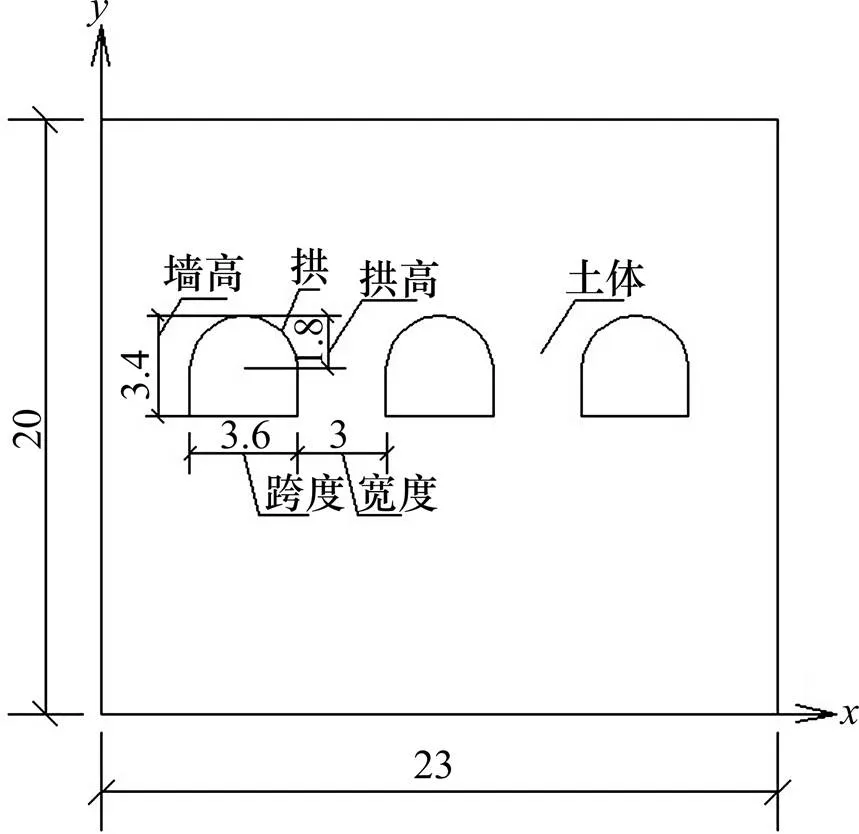
图5 计算范围

为了核验全长黏结柔性锚固系统对受锚靠崖窑体结构的适用性和有效性的影响，主要研究3个时间段的塑性区特征和位移分布情况。通过开挖锚固的方式加固窑洞土体结构导致的塑性区分布状况以及对窑体结构顶部土体垂直位移进行跟踪计算，达到研究全长黏结锚固系统的有效性。数值分析数据见图7所示。

图6 网格的划分

表1 计算力学参数

(a) 5个月；(b) 1 a；(c) 2 a

从图7数值计算垂直位移分布云图可分析出：受锚窑洞的垂直位移初期变化率很显著并且是指向窑体下部的负位移。但随着蠕变时间的持续延迟，锚固结构的强度得到发挥后其垂直位移变化渐渐减缓，最大位移只是分布在窑洞顶的局部小范围内。受锚窑洞在全长黏结锚固加固的2 a时间内,其最大垂直位移为2.5 cm，因此，全长锚固柔性支护对加固靠崖窑的稳定性具有明显效果。

图8 剪应变率

图9 塑性区分布

从图8剪应变率云图可以得到：当窑体结构经过预应力锚杆支护后，窑体结构剪应变分布在2.05×10−5~1.75×10−5，剪应变率最大值主要分布在洞体结构的拱曲线、侧面墙和下部窑腿区域，最小剪应变率范围主要分布在未受影响的土体中，加固效果好。

从图9塑性区分布云图可以看出：受锚杆加固后，窑洞结构在荷载松弛后的破坏形式主要是拉伸破坏和剪切破坏，没有出现连续连通的破坏塑性区。当塑性区处于锚杆加固范围内时，且集中在拱间土区域，加固效果更加明显。

4 结论

1) 建立了靠崖窑优势垂直节理裂隙土体的翼形裂纹和共线裂纹模型，得出了翼形裂纹折算长度的计算式和应力强度因子的计算式。

2) 依据靠崖窑土体的变形特点，建立改进的Burgers非线性蠕变模型，能够完全描述土体材料的瞬弹、塑性、黏性和黏弹性共存的变形性质，能够反映蠕变的全过程，即衰减蠕变、稳定蠕变和加速蠕变。

3) 算例表明，拉伸和剪切塑性区是靠崖窑的主要塑性区。在土体蠕变固结效应影响下，在窑洞拱曲线、窑腿周围土体和上覆土层的区域会出现大量的剪切和拉伸塑性区，并向上延伸到地表，且窑洞土体主要表现为剪切破坏。

[1] Mohamed Ben Mansour, Ahmed Jelidi, Amel Soukaina Cherif, et al. Optimizing thermal and mechanical performance of compressed earth blocks (CEB)[J]. Construction and Building Materials, 2016, 32(1): 23−27.

[2] Ernest Bernat-Maso, Lluís Gil, Christian Escrig. Textile- reinforced rammed earth: Experimental characterisation of flexural strength and thoughness[J]. Construction and Building Materials, 2016, 32(5): 31−36.

[3] 张丽辰, 吴孔友, 何文军, 等. 准噶尔盆地北三台凸起断裂结构特征及成岩封闭作用[J]. 地质力学学报, 2018, 24(5): 607−616. ZHANG Lichen, WU Kongyou, HE Wenjun, et al. Structural characteristcs and diagenetic sealing of faulsts in the Beisantai swell Junggar basin[J]. Journal of Geomechanics, 2018, 24(5): 607−616.

[4] 童丽萍, 韩翠萍. 黄土材料和黄土窑洞构造[J]. 施工技术, 2008, 37(2): 107−108. TONG Liping, HAN Cuiping.Loess material and construction of loess caves[J]. Construction Technology, 2008, 37(2): 107−108.

[5] 卫峰, 马瑞生, 张有仁. 土窑洞抗震性能探讨[J]. 工程抗震, 1993(1): 43−46. WEI Feng, MA Ruisheng, ZHANG Youren. Discussion on seismic behavior of earth cave dwelling[J].Earthquake Resistant Engineering, 1993(1) : 43−46.

[6] 陈国兴, 张克绪, 谢君斐. 黄土崖窑洞抗震性能分析[J]. 哈尔滨建筑工程学院学报, 1995, 28(1): 15−21. CHEN Guoxing, ZHANG Kexu, XIE Junfei. Aseismic performance anlysis of the cave dewlling on the loess precipice[J]. J Harbin Archit & Civ Eng Inst, 1995, 28(1): 15−21.

[7] 吴成基, 甘枝茂, 孟彩萍. 陕北黄土丘陵区窑洞稳定性分析[J]. 陕西师范大学学报(自然科学版), 2005, 33(3): 119−122. WU Chengji, GAN Zhimao, MENG Caiping.Stability of cave dwelling of loess hills in north part of Shaanxi province[J].Journal of Shaanxi Normal University (Natural Science Edition), 2005, 33(3): 119−122.

[8] LIU Weixin, Wynne, Judson. Cave millipede diversity with the description of six new species from Guangxi, China[J].Subterranean Biology, 2019, 30(7): 57−94.

[9] 杨延毅．节理裂隙岩体损伤断裂力学模型及其在岩体工程中的应用[D]. 北京: 清华大学, 1990. YANG Yanyi. Damage and fracture mechanics model of jointed rock mass and its application in rock mass engineering[D]. Beijing:Tsinghua University, 1990.

[10] 陆毅中. 工程断裂力学[M]. 西安: 西安交通大学出版社, 1986.LU Yizhong.Engineering fracture mechanics[M]. Xi’an:Xi’an Jiaotong University, 1986.

[11] 杨焜, 张风亮, 朱武卫, 等. 靠崖式黄土窑洞结构传力机制研究[J]. 工业建筑, 2019, 49(1): 31−38. YANG Kun, ZHANG Fengliang, ZHU Wuwei, et al. Research on the force transfer mechanism of loess cave dwelling by cliff[J].Journal of Industrial Construction, 2019, 49(1): 31−38.

[12] MA Yunlong, XIA Feng, ZHAN Lihua, et al. Study on multi-step creep aging behavior of Al-Li-S4 alloy[J]. Metals, 2019, 9(7): 21−26.

[13] REN Xiaodan, WANG Qing, Roberto Ballarini, et al. Coupled creep-damage-plasticity model for concrete under long-term loading[J]. Journal of Engineering Mechanics, 2020, 146(5): 37−41.

[14] 袁海平, 曹平, 许万忠, 等. 岩石黏弹塑性本构关系及改进的Burgers蠕变模型[J]. 岩土工程学报, 2006, 28(6): 796−799. YUAN Haiping, CAO Ping, XU Wanzhong, et al.Visco- elastop-lastic constitutive relationship of rock and modified Burgers creep model[J].Chinese Journal of Geotechnical Engineering, 2006, 28(6): 796−799.

[15] 王军保, 刘新荣, 王铁行. 基于改进分数阶黏滞体的岩石非线性蠕变模型[J]. 中南大学学报(自然科学版), 2015, 46(4): 1461−1467. WANG Junbao, LIU Xinrong, WANG Tiehang. A nonlinear creep model for rocks based on modified fractional viscous body[J].Journal of Central South University (Science and Technology), 2015, 46(4): 1461− 1467.

[16] Lepakshi R, Venkatarama Reddy B V. Shear strength parameters and Mohr-Coulomb failure envelopes for cement stabilised rammed earth[J]. Construction and Building Materials, 2020, 249(4): 11−13.

Research on fracture characteristics and time stability of underground cavern structure

LI Yun1, LIU Ji1, WANG Jun2

(1. Hungn Urban Construction College, Department of Construction Equipment Engineering, Xiangtan 411101, China;2. Hunan Institute of Engineering, College of Building, Xiangtan 411101, China)

According to the crack distribution and deformation characteristics of the kiln structure under complex conditions, through the fracture mechanics characteristics of the vertical dominant joint fracture LOESS, the spreading trend of the wing-shaped crack was analyzed, and the wing-shaped crack and collinear crack model of the soil body with the dominant vertical joint crack in the cliff kiln was established. The calculating formula of the length of wing crack commutation and the calculating formula of stress intensity factor were obtained. The displacement expression and anchorage load calculation of the Burgers creep model were also obtained. The results show that the model of fracture and creep reflects the displacement and plastic distribution of the kiln structure and the stability of aging. The results can provide useful reference for the reinforcement design of kiln structure.

underground kiln structure; fracture characteristics; creep model; reniforcement and stability

TU45

A

1672 − 7029(2020)09 − 2346 − 08

10.19713/j.cnki.43−1423/u. T20200390

2020−05−11

湖南省自然科学基金资助项目(2019JJ40056)；湖南省社科基金资助项目(18YBJ29)；湖南省教育科学“十三五”规划课题资助项目(XJK19CZY056)；湖南省教育厅重点科学研究项目(18A345)

李云(1975−)，女，湖北孝感人，副教授，从事土木工程与智能建筑的教学与研究；E−mail：liyunliuji@163.com

(编辑 阳丽霞)