关节轴承转角分析及优化方法研究

邹 衍，赵振贵，黄志军，傅琳晖

（航空工业洪都，江西 南昌，330024）

0 引言

作动筒和缓冲器是飞机起落架、舱门等机构设计中常用的功能部件，且工作时都为往复直线运动[1]。作动筒和缓冲器两端一般采用关节轴承与其他部件连接，工作中，与其他连接部件形成一个空间曲柄滑块机构。缓冲器设有扭力臂[2]，工作时外筒与活塞间无相对转动；作动筒一般不设扭力臂，但工作中应尽量避免外筒与活塞间相对转动。所以，任一时刻，作动筒和缓冲器可简化为一连杆，如图1所示。连杆两端通过关节轴承与其他部件连接。连杆运动可描述为绕关节轴承安装轴的转动以及绕自身轴线的转动。由于连杆两端都为关节轴承，理论上连杆绕自身轴线的转动是一个无法约束的自由度，连杆可以自由转动，但实际上，受关节轴承结构限制，连杆绕自身旋转只能在一定范围内转动。

如图2所示为关节轴承示意图，关节轴承由内圈和外圈构成，受其结构限制，关节轴承工作中转动范围受限，其最大转角为α。最大转角的大小影响到关节轴承的尺寸及承载能力，选择合适最大转角的关节轴承是机构设计中的关键环节。

图1 双关节轴承连杆示意图

图2 关节轴承示意图

1 关节轴承转角计算分析方法

如图1所示，两关节轴承分别命名为关节轴承1和关节轴承2。O1为关节轴承1中心，d1v为关节轴承1内圈安装轴线上任意一点；O2为关节轴承2中心，d2v为关节轴承2内圈安装轴线上任意一点。

1.1 关节轴承内圈安装轴线与连杆轴线夹角

在某全局坐标系下，测量连杆部件整个工作过程中点O、dv和dn的坐标，则根据各点坐标，可计算得任意时刻i关节轴承内圈安装轴线向量v1i、v2i和连杆轴线向量ni。

根据余弦定理可知，任意时刻i，关节轴承内圈安装轴线向量v1i、v2i和连杆轴线向量ni夹角

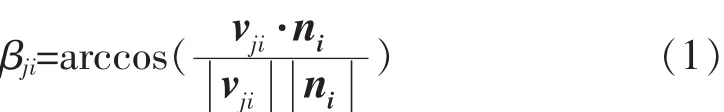
其中，j=1、2，分别表示关节轴承1和关节轴承2。

所以关节轴承实际需求转角

若连杆两端采用相同型号关节轴承，则关节轴承最大转角α必须满足

1.2 绕连杆轴线自转角

如图3所示，以关节轴承1安装轴线和连杆轴线确定的平面为A1，连杆与关节轴承1连接端平面为B1，关节轴承1上端面为C1，向量m1i为平面B1法向量，向量v1i为平面C1法向量。连杆与关节轴承2连接端平面为B2，关节轴承2上端面为C2，向量m2i为平面B2法向量，向量v2i为平面C2法向量。当A1⊥B1时设为零位。如图4所示，连杆在零位绕连杆轴线顺时针旋转θ1i（全文按右手定则确定转角正负）后，关节轴承达到最大转角，此时平面B1法向量为向量m’1i，则

图3 双关节轴承连杆定义平面示意图

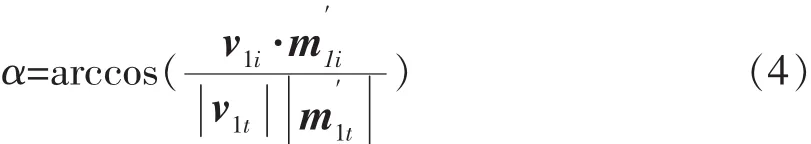
如图5所示，当连杆处于零位时，平面A1的法向量为 p1i，则

图4 连杆绕轴线旋转示意图

图5 连杆零位状态示意图

其中，R(n1i,θ1i)为向量 m1i绕 n1i旋转 θ1i角的变换矩阵。

对于空间任一向量v，其绕空间任一单位向量n旋转θ的变换矩阵[3]通式为

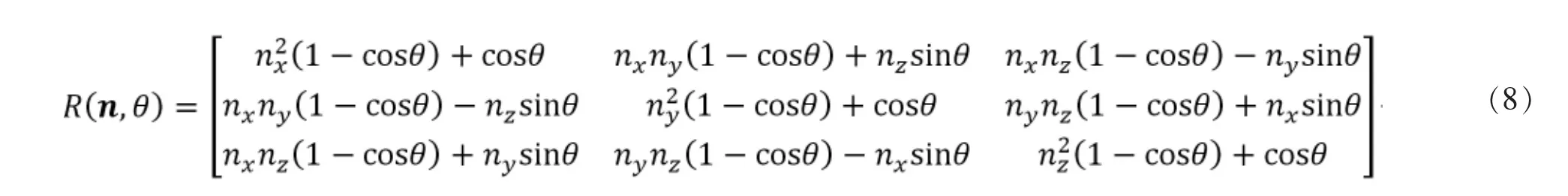
通过式（4）～（8）即可计算得关节轴承1达到最大转角时，连杆绕连杆轴线顺时针旋转角θ1i，记为最大值θ1imax。显然，连杆绕连杆轴线逆时针旋转θ1i时，关节轴承1同样达到最大转角，记为最小值θ1imin=-θ1i=-θ1imax。

对于关节轴承2，任意时刻i向量m1i与向量m2i相对位置是固定的，其转换关系可定义为m1i绕p1i旋转φ1，再绕ni旋转φ2，如图6所示。 所以

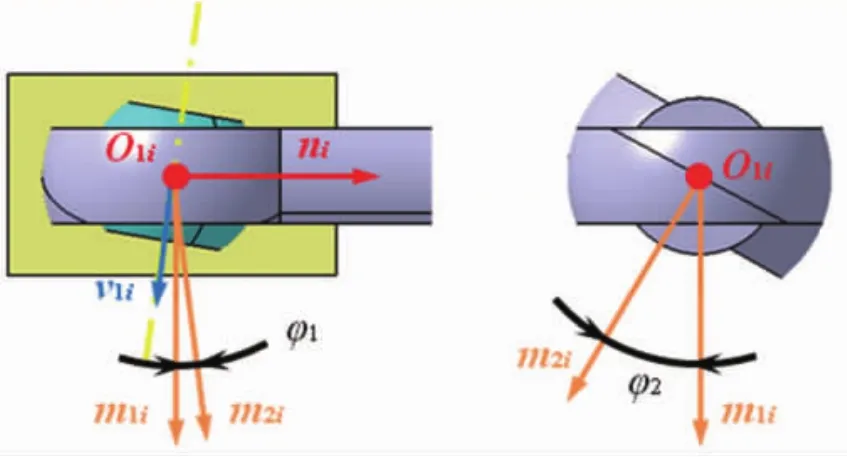
图6 平面法线变换图

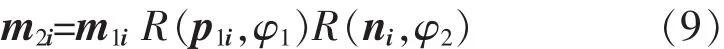
与关节轴承1类似，根据式（4），可计算得关节轴承2达到最大转角时，连杆绕连杆轴线旋转角最大值θ2imax和最小值 θ2imin。

所以，任意时刻i，连杆绕连杆轴线旋转角最大值和最小值分别为

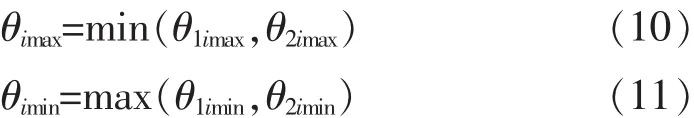
为保证连杆能够正常工作，连杆绕连杆轴线旋转角度范围必须大于0，即

当连杆两头可相对旋转时（如：不带扭力臂的作动筒），若连杆绕连杆轴线旋转角度范围小于0，说明连杆在工作中连杆两头会发生相对转动（如：作动筒活塞与外筒绕轴线相对旋转）。

1.3 关节轴承选用准则

根据前2节分析可知，采用双关节轴承的连杆（自身无相对转动，如带扭力臂的作动筒和缓冲器），选用关节轴承必须保证其全工作过程中满足

1.4 实例验证

如图7所示为某空间曲柄滑块机构，此时作动筒行程为0。系统由基座，摇臂和作动筒（活塞和外筒）组成，摇臂可绕基座旋转，作动筒两端通过同型号关节轴承分别与摇臂和基座连接，连接外筒和基座的为关节轴承1，连接活塞与摇臂的为关节轴承2。

图7 某空间曲柄滑块机构

选用关节轴承最大转角为22°，作动筒行程与关节轴承相关角度关系如图8和图9所示，相关参数统计如表1所示。

图8 作动筒行程与轴线夹角曲线

图9 作动筒行程与自转角曲线

表1 关节轴承参数统计表

由图8可知，关节轴承1安装轴线与作动筒轴线夹角随着作动筒行程增大而增大，关节轴承2安装轴线与作动筒轴线夹角随着作动筒行程增大而减小。整个过程中，关节轴承最大夹角不超过17°。

由图9可知，作动筒绕自身轴线转动的自转角范围随着作动筒行程增大而先增大后减小。整个过程中自转角范围大于28°。

由上可知，在当前结构设计下，选择最大转角为22°的关节轴承能满足功能要求，且余度较大。

2 关节轴承安装轴优化设计

由1.4节实例分析可知，对于该空间曲柄滑块机构，选择最大转角为22°的关节轴承能够满足机构功能要求，但是存在一些问题：

1）关节轴承最大转角较大，零件需要定制，转角过大也加大了系统的重量；

2）作动筒行程最小和最大时为机构主要承载工况，此时关节轴承安装轴线与作动筒轴线夹角较大，影响关节轴承的承载能力；

3）两关节轴承安装轴线不平行，机构进行拆装时较困难。

因此，对该空间曲柄滑块机构关节轴承安装轴进行优化。

2.1 优化原则

对该空间曲柄滑块机构关节轴承安装轴进行优化遵循以下原则：

1）关节轴承最大转角尽量小；

2）作动筒行程最小和最大时，关节轴承安装轴与作动筒轴线夹角尽量小；

3）作动筒行程最小时进行装配，保证此时关节轴承安装轴平行。

2.2 优化方法

如图10所示，在安装状态，以关节轴承1中心为原点O1，与之连接部件（基座）上参考点d11和d12建立任意坐标系O1x1y1z1，关节轴承2中心为原点O2，与之连接部件（摇臂）上参考点d21和d22建立任意坐标系O2x2y2z2。保证两坐标系对应坐标轴相互平行。关节轴承优化安装轴通过两个角度进行定位：以Ox为基准，先绕Oz旋转α1，再绕Ox旋转α2。由于两坐标系平行，可以任一坐标系为基准进行变换。

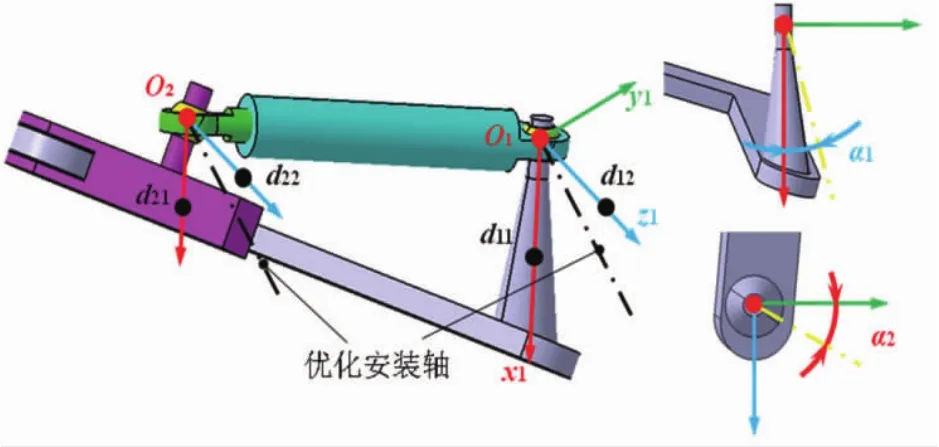
图10 旋转轴定位图

则任意时刻i，优化安装轴向量

再根据第2节计算分析方法，获取不同定位角α1和α2时满足关节轴承转角设计要求的设计参数，最后根据优化原则，选择最佳设计方案。

2.3 实例验证

保证安装状态时关节轴承安装轴平行，关节轴承最大转角初步定为15°。

定位角α1=8°时，关节轴承相关参数与定位角α2关系如图11所示。

图11 α1=8°时关节轴承相关参数与α2关系图

由图 11 可知， 当定位角 α1=8°，α2为 160°～240°时，满足关节轴承选用准则。改变定位角α1，曲线分布规律与图11类似，α2有效范围略有变化。

考虑到余度设计，设定连杆绕连杆轴线自转角角度范围不小于5°，最终确定优化安装轴定位角α1=8°、α2=226°，关节轴承相关参数如表 2 所示。

表2 优化后关节轴承参数统计表

优化前后，该空间曲柄滑块机构对比图如图12所示。整个运动过程中，关节轴承参数与作动筒行程关系对比图如图13和图14所示。

图12 机构优化前后对比图

3 结论

本文结论如下：

1）建立了双关节轴承连杆关节轴承转角计算分析方法,确立了选用准则,即利用向量法计算全工作过程中关节轴承内圈安装轴线与连杆轴线夹角和绕连杆轴线自转角,合理设计方案需满足轴承内圈安装轴线与连杆轴线夹角工作过程始终小于选用关节轴承最大转角,且自转角始终大于零。

图13 作动筒行程与轴线夹角对比曲线

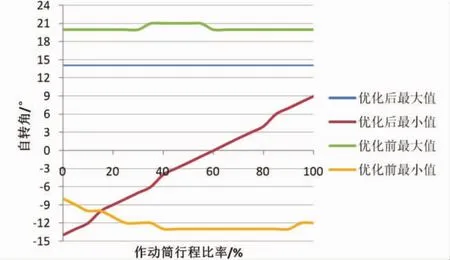
图14 作动筒行程与自转角对比曲线

2）根据受力及安装合理性制定了双关节轴承连杆内圈安装轴线优化原则,提出了关节轴承内圈安装轴优化方法,即初始设计安装轴通过两次旋转获得若干优化安装轴,再利用本文建立的计算分析方法及选用准则确定最终优化安装轴。

3）通过实例验证了本文建立的双关节轴承连杆关节轴承转角计算分析方法和内圈安装轴线优化方法的合理性和可行性。本文建立的方法可用于工程设计中，为结构设计优化提供了理论依据。