1580 mm运输线步进梁改造设计
周治宇 王 勇 汪建国
(马钢集团设计研究院责任有限公司,安徽230000)
1580 mm热轧钢卷运输线是马钢股份第四钢轧总厂的一条热轧生产线,成品库有两台步进梁,位于卸卷台架和钢卷运输线之间,其主要作用是将钢卷从卸卷台架上卸下后,运送至打捆位打捆,打捆完成后,将钢卷输送到位于运输辊道上的钢卷托盘上,针对这两台步进梁中原运行中的问题进行分析,提出了改进措施。
1 原步进梁问题探讨
1.1 步进梁动梁的动作过程
步进梁动梁动作分横移动作和升降动作,分别由横移液压缸和升降液压缸驱动。当卸卷台架放上钢卷时,横移液压缸伸出,动梁的一端由起始位移至钢卷下,然后升降液压缸推着动梁提升,钢卷被抬离卸卷台架,提升到位后,横移液压缸缩回,动梁带着钢卷前进一个步距,到位后升降液压缸下降,将钢卷放在固定鞍座上。反复动作,将钢卷一步一步输送前进。
1.2 原步进梁结构
原步进梁是由两个横移小车分别各支承一个升降液压缸,垂直顶升动梁完成步进梁的提升动作,横移液压缸推动动梁完成步进梁的横移动作。这种横移小车形式的步进梁设计在运行过程中存在车轮跑偏、啃轨及升降液压缸易损坏的情况。当液压缸损坏时,更换备件也极为麻烦,需要将整个动梁吊出,才能进行液压缸的更换。原步进梁结构如图1所示。
1.3 问题分析
由于原步进梁升降液压缸垂直作用于动梁底部,两个升降液压缸缸杆的扁头完全受钢卷与动梁的载荷,受力较大;同时动梁在上升至高点位置时,升降液压缸缸杆伸出位置大,横移液压缸作用于动梁上时,此时对升降液压缸缸杆有一个力矩,使图2中A处形成一定角度,损坏液压缸缸杆底部的密封,从而导致液压缸损坏。
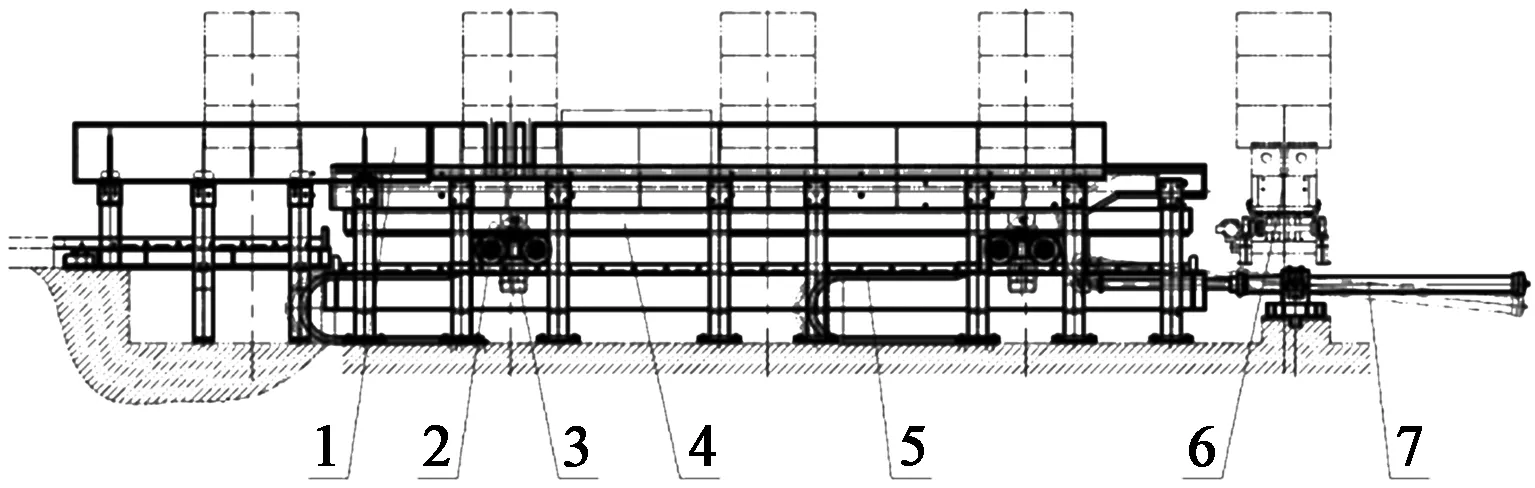
1—固定鞍座 2—横移小车 3—升降液压缸 4—动梁 5—拖链 6—卸卷台架 7—横移液压缸图1 原步进梁图Figure 1 The former walking beam
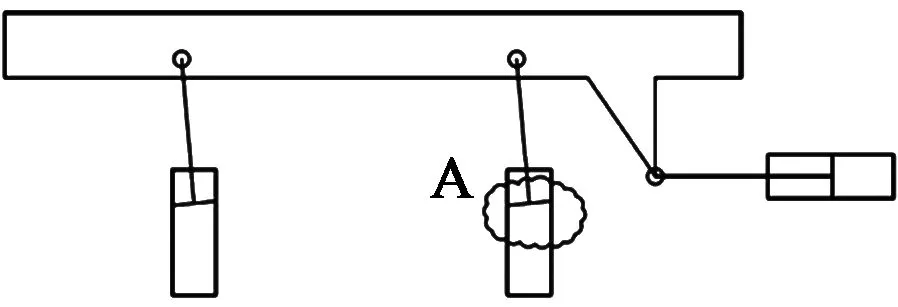
图2 原步进梁油缸密封损坏分析图Figure 2 Analysis on the former walking beam oil cylinder seal damage
2 步进梁的改进结构
为改变原来步进梁缸的受力情况,现采用一种由两个四连杆机构组成的步进梁,改进后的步进梁如图3所示。四连杆机构的步进梁具有良好的分散液压缸受力的特点,甚至在连杆与梁垂直位置时,理论上液压缸不受其推力。可以很好地改善了原升降液压缸受力过大的情况,同时避免了升降液压缸密封受损的情况;如若需要更换缸,由于两个四连杆机构由中间连杆连接,保证一个缸也可以保持平衡,无需再将梁重新吊出,减少了更换缸的工作。
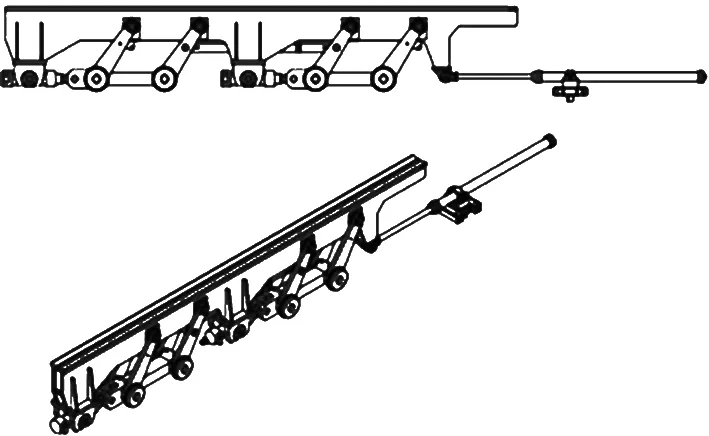
图3 改进后的步进梁图Figure 3 Improved walking beam
改进后步进梁升降液压缸参数:缸径250 mm;杆径180 mm;行程950 mm;压力25 MPa。
横移液压缸(利旧)参数:缸径200 mm;杆径140 mm;行程4000 mm;压力25 MPa。
2.1 升降液压缸受力分析
(1)动梁自重与所有钢卷的重量之和为FN,两组升降液压缸中动梁的理论设计受力点中两组液压缸受力均衡,受力分别约为0.5FN。
(2)图4为升降液压缸一中间位置,升降系统中,与动梁连接的连杆一、连杆二和升降液压缸均受到来自动梁的压力,分析升降液压缸在此位置所受压力的公式即可得到升降液压缸所需的推力,从而选择相应的液压缸。
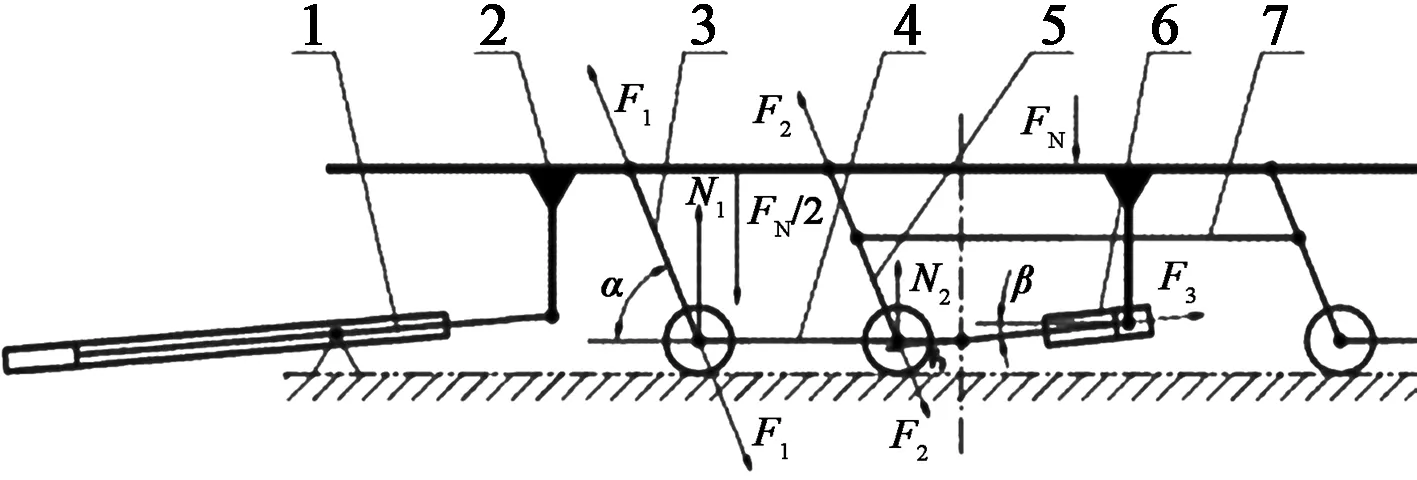
1—横移液压缸 2—动梁 3—连杆一 4—下连杆 5—连杆二 6—升降液压缸 7—中间连杆图4 步进梁一个升降系统结构简图Figure 4 A lift system structure of walking beam
(3)升降过程的动态分析中,已知连杆一与水平面夹角为α,升降液压缸与水平面的夹角为β,可以单独对动梁或者下连杆进行受力分析,求出升降液压缸在此动态位置所需要的推力。
以动梁单独分析为例。
动梁总共受到了四个力:连杆一所受压力的反力F1;连杆二所受压力的反力F2;升降液压缸推力的反力F3;动梁与钢卷的重力FN/2。这四个力平衡组成力学三角形,根据正弦定理得出:
故有升降液压缸理论推力公式:
2.2 升降液压缸所需推力
根据动梁与连杆的设计尺寸,连杆一与水平面夹角α与升降液压缸与水平面的夹角β间存在一个与梁各个尺寸相关的关系公式。改进步进梁最大负荷的是四个钢卷,每个钢卷直径最大2100 mm,单重约40 t,动梁自重26 t,总重FN=186 t,取FN=200 t,最终获得理论推力计算结果见表1。
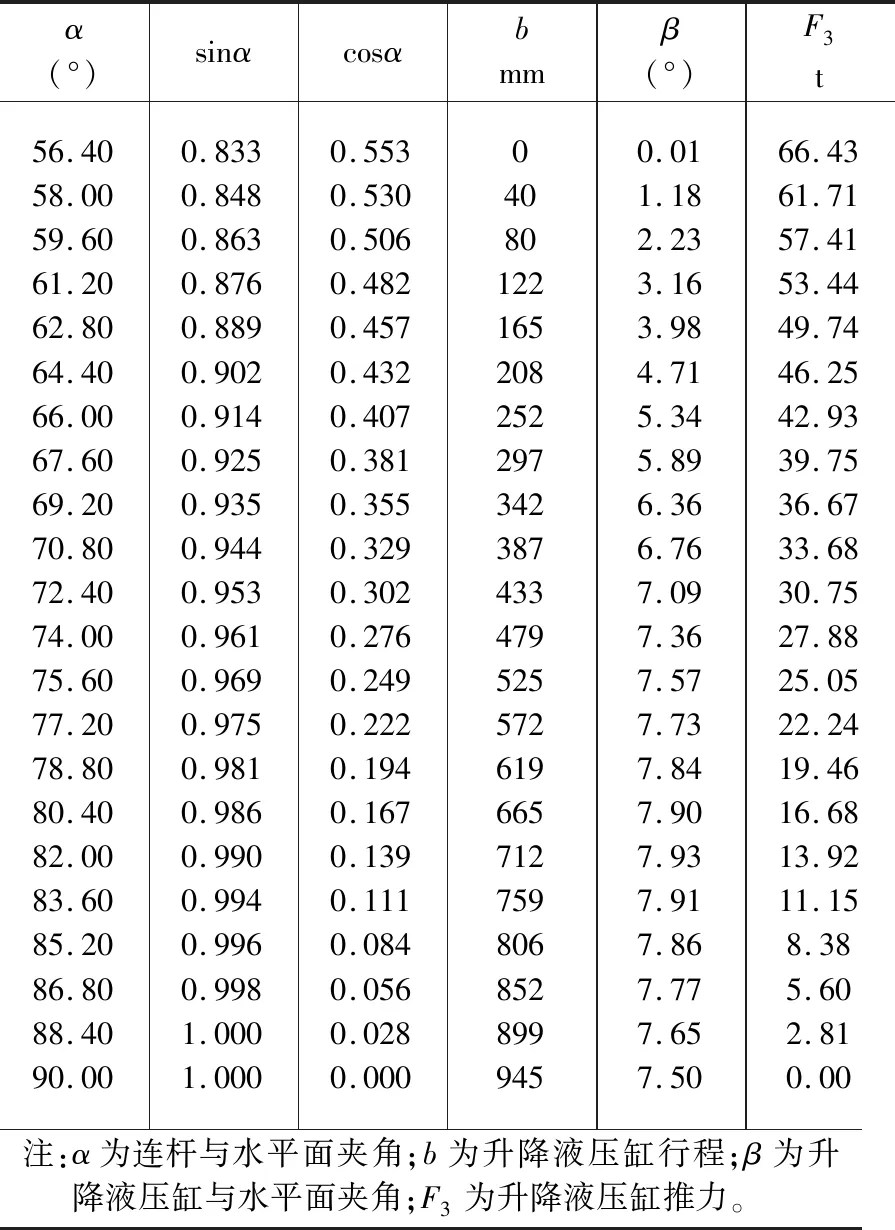
表1 升降液压缸理论推力计算结果Table 1 Theoretical thrust calculation results of lift hydraulic cylinder
由此发现当取FN=200 t时,原结构单个升降液压缸所需推力约100 t,而改用四连杆机构后,在初始位置时,升降液压缸所受推力最大约67 t;随着动梁的提升,升降液压缸推力逐渐衰减,最后下降为零,大大改善了缸的受力情况。
2.3 动梁结构设计
动梁在最高点时可以简化为如图5所示。
图5中动梁的受力拥有四个支点,无法用简支梁求解,所得到的平衡表达式(1)为:
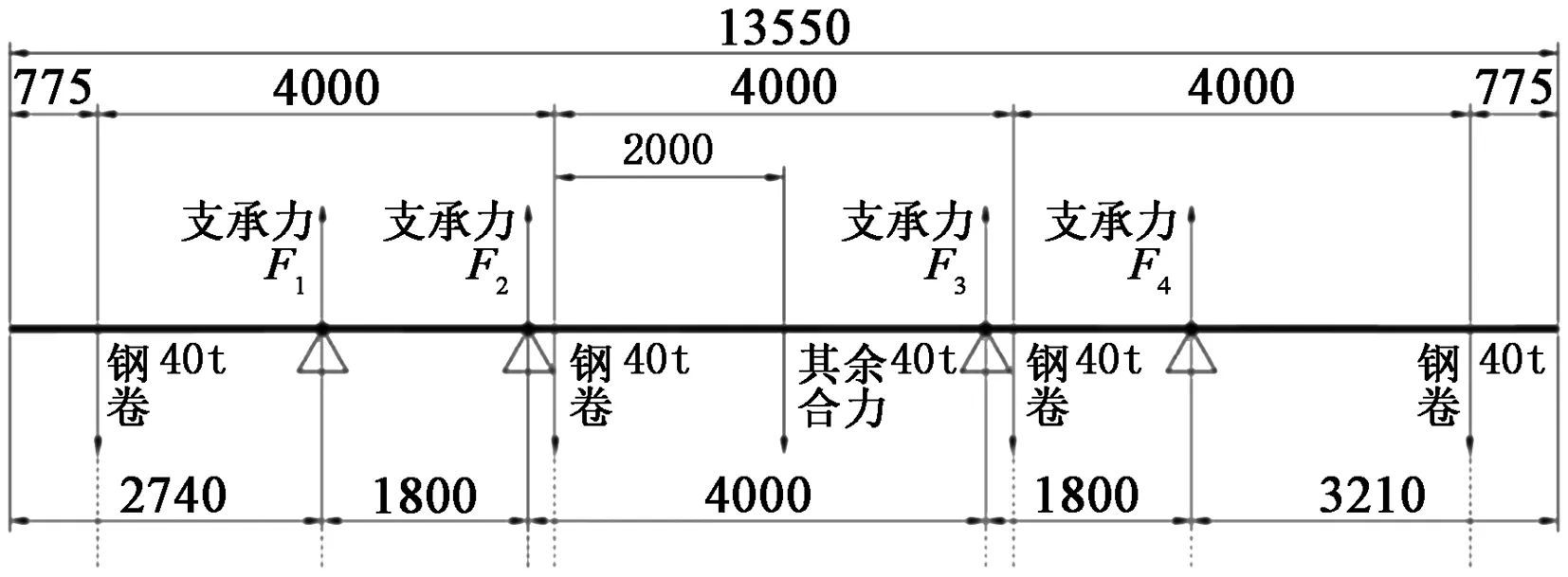
图5 动梁在最高点受力图Figure 5 Force of moving beam at the highest point
F1+F2+F3+F4=40×4+40
F1×2740+F2×4540+F3×8540+F4×10440=
40×(775+4775+6775+8775+12775)
平衡表达式数量小于求解的支座反力数量,是一个超静定问题,下面对此求解。
根据挠度求超静定梁支反力,上述梁受力点多,可将其转化为三种结构,依次求每种结构在支点F2与支点F3的挠度。
(1)结构一
动梁结构一如图6所示,此梁有挠度公式:
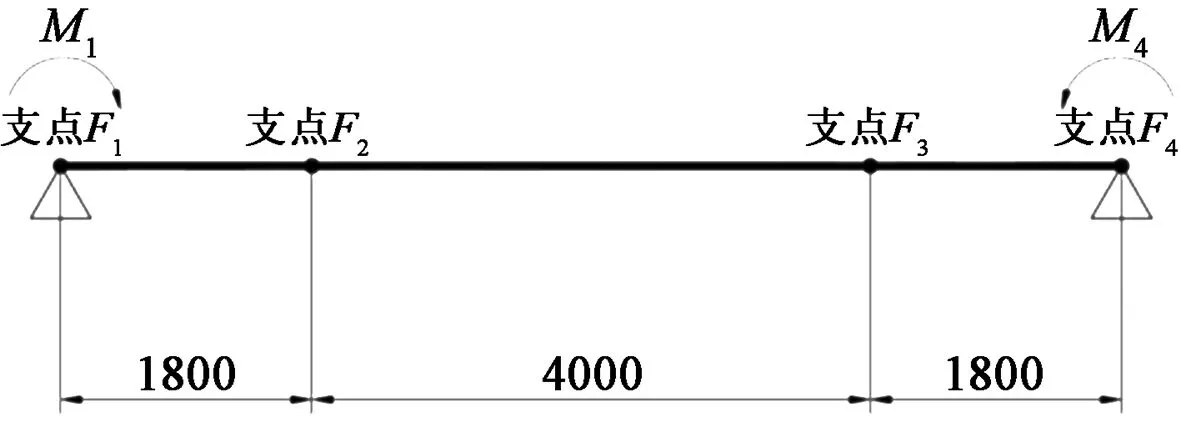
图6 动梁结构一Figure 6 The first moving beam structure
式中,M1=-40×1965;M2=-40×2435;l=7600 mm;ξ=x/l。
将相应数据带入公式得出:
EIf1(1800)=-454 980 140 800
EIf1(5800)=-472 137 171 200
(2)结构二
动梁结构二如图7,此简单梁有挠度公式:
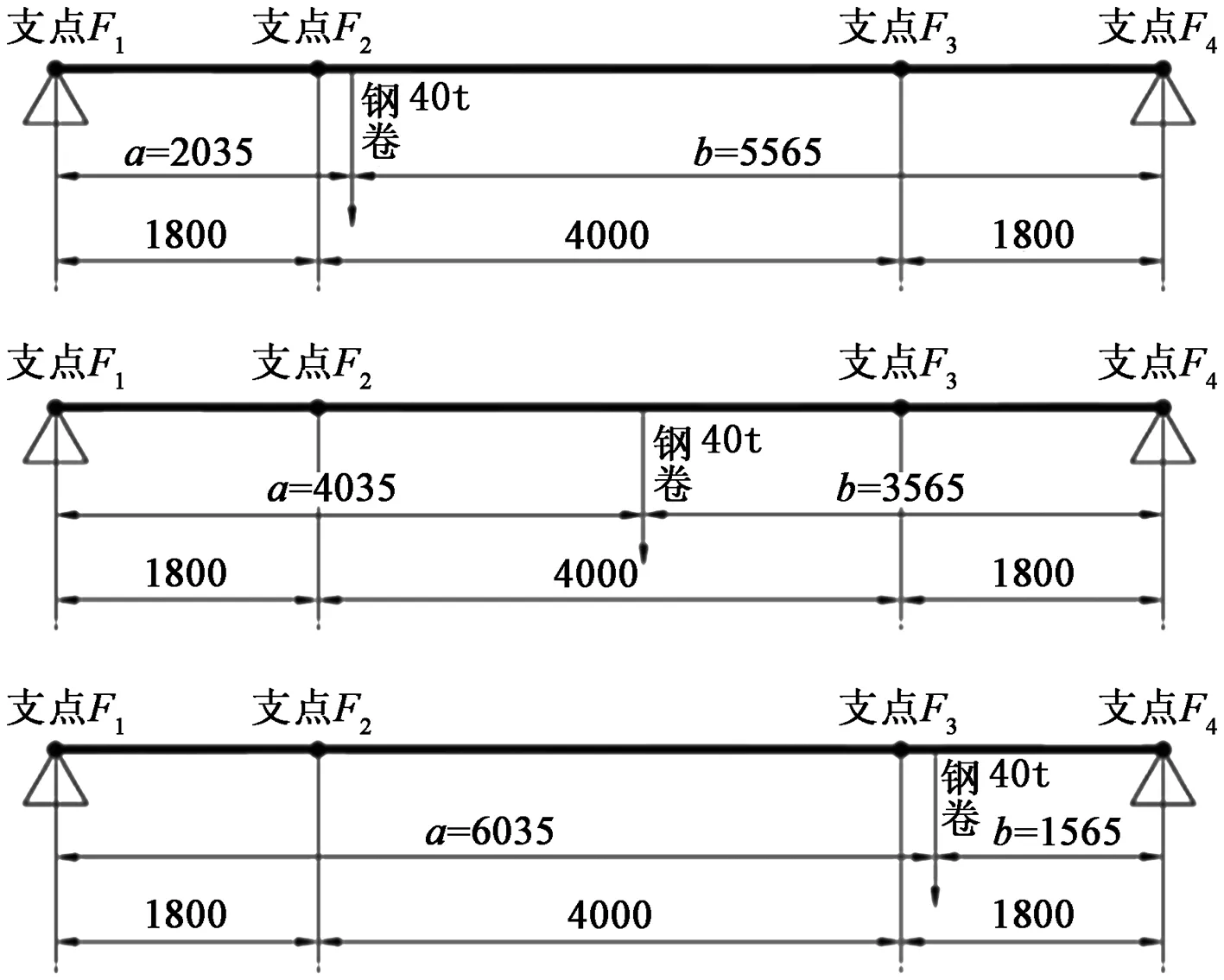
图7 动梁结构二Figure 7 The second moving beam structure
其中l=7600 mm;ξ=x/l;ζ=(l-x)/l。
将相应数据带入公式得出:
EIf2(1800)=570 957 218 882
EIf2(5800)=578 045 000 285
(3)结构三
动梁结构三如图8所示,结构三与结构二公式雷同,只需将挠度取结构二中公式的相反数,故有:
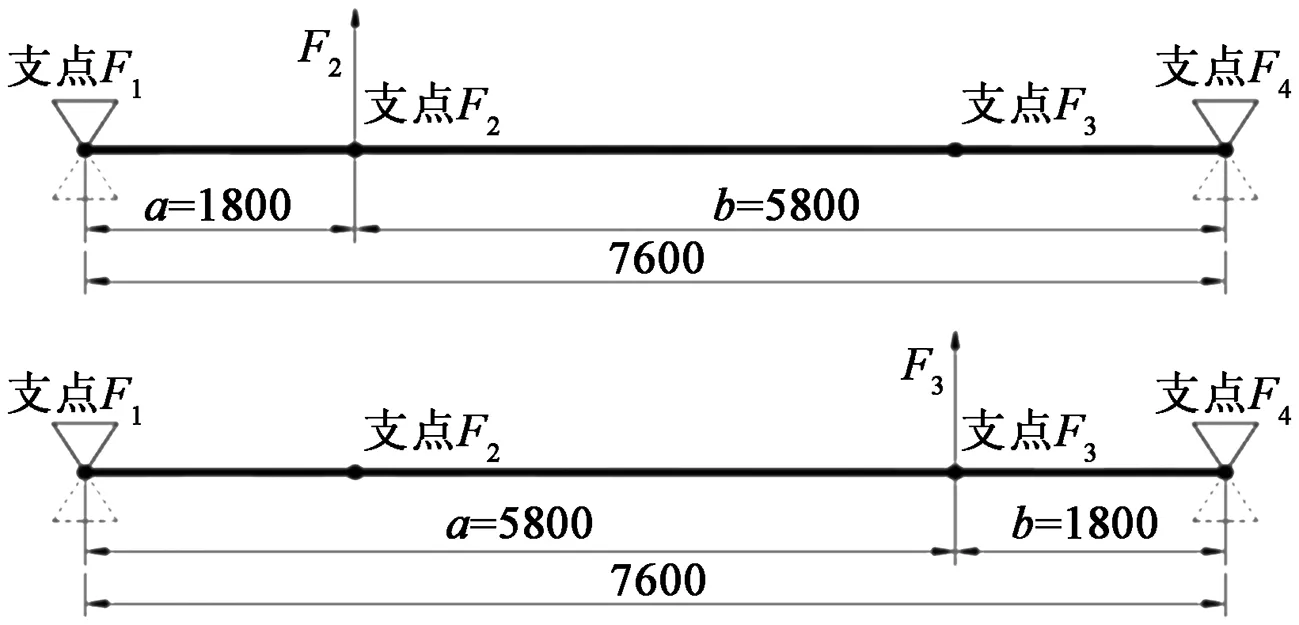
图8 动梁结构三Figure 8 The third moving beam structure
EIf3(1800)=4 803 321 600F2+3 680 467 200F3EIf3(5800)=3 680 467 200F2+4 803 321 600F3
由于支点的挠度为零,所以有:
EIf1(1800)+EIf2(1800)+EIf3(1800)=0
EIf1(5800)+EIf2(5800)+EIf3(5800)=0
由平衡表达式(1)解出:
F1=79.8 t;F2=17.6 t;F3=7.6 t;F4=95 t。
根据梁的所有力做出相应剪力图与弯矩图(见图9)。从图9可知在A处弯矩最大,为:
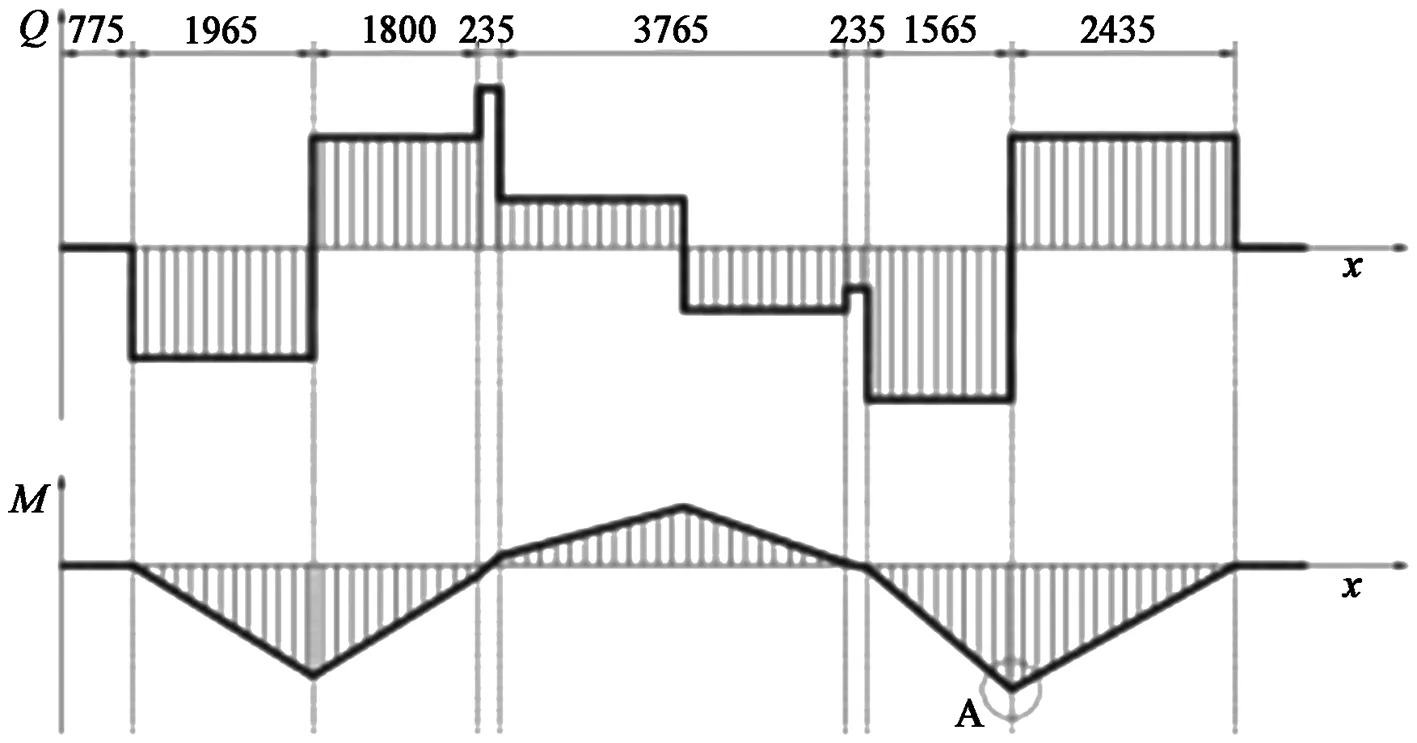
图9 动梁的剪力图与弯矩图Figure 9 Shear force and bending moment of moving beam
MA=40×10000×2435×10-3=9.74×105N·m
设计结构中梁截面(见图10)的抗弯截面系数为:
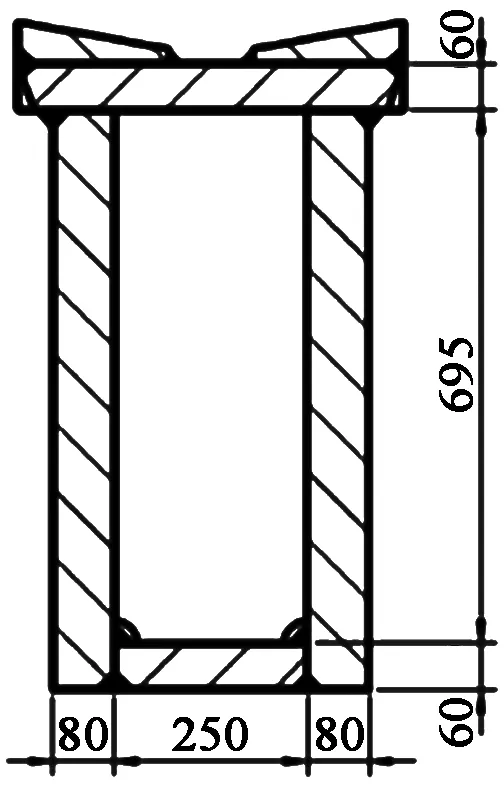
图10 动梁的截面图Figure 10 Section of moving beam
WX=(BH3-bh3)/6H=6.26×107mm3
[σ]=MA/WX=15.6 MPa<[σp],梁的截面满足强度条件。
3 结语
通过将步进梁升降液压缸的作用形式改为四连杆机构,解决了原先升降液压缸易损坏不易更换的问题,目前此改造设计已投入使用,效果良好,达到了改进设计的目的。

