基于自助法的高斯贝叶斯网结构学习

徐平峰, 王树达, 尚来旭, 杨 哲

(长春工业大学 数学与统计学院， 吉林 长春 130012)

0 引 言

贝叶斯网是概率论和图论的有机结合，其图结构是一个有向无圈图(DAG)，可清晰直观地表示变量间的条件独立关系、因果关系和变量间的依赖关系。在贝叶斯网领域中，结构学习是一类非常重要的研究问题，即从观测数据出发探求变量间的条件独立关系。

结构学习方法大致分为三类:

1)基于约束的方法。这类方法依赖于条件独立关系检验，其典型代表是PC算法[1]。该算法首先进行低阶条件独立性检验，然后逐步进行高阶条件独立性检验，排除不可能的边，建立有向无圈图的骨架，确定v结构，最后尽可能地为边添加方向，找到一个等价类。

2)基于评分搜索的方法。该方法为每个DAG赋一个评分，然后在搜索空间内搜索一个得分最低的DAG或等价类。例如,Chickering[2]提出了贪婪等价类搜索(GES)方法，通过逐步向前和向后搜索得到得分最小的等价类；在误差等方差的条件下，Peters 等[3]利用贪婪DAG搜索方法(GDS)求BIC评分最小的高斯贝叶斯网。若先利用l1惩罚似然学习高斯图模型的无向图，然后在贪婪搜索时保证DAG的骨架是该无向图的边，这时搜索DAG的范围将变小，该方法称为GDSM。

3)混合方法。分两个阶段：

a)限制阶段，先进行一些条件独立性检验，利用检验结果排除大量的边，以减小候选DAG的空间；

b)得分搜索阶段，在这些条件独立性关系的约束下，搜索评分最低的DAG。例如，Tsamardinos等[4]提出MMHC算法，先采用基于约束的方法找到一个顶点可能的父顶点和子顶点，然后搜索BDe得分最小的DAG。

近些年，基于自助法(Bootstrap)的模型聚合方法已经应用到很多领域，如高维数据的变量选择(Bach[5]，Wang等[6])和高斯图模型的结构学习(Meinshausen等[1]，Li[8]);Elidan[9]利用Bootstrap数据集计算稳健的模型选择准则。对于每个数据集和一个给定的DAG，求此DAG参数的极大似然估计，进而利用聚合的信息准则来衡量G;Wang 等[10]提出了一种基于Bootstrap的DAG结构学习方法，称为DAGBag。该方法基于数据的Bootstrap重采样学习DAG集合，以结构海明距离(SHD)为度量，通过最小化到整个DAG集合的总距离来导出聚合DAG。

文中提出一种新的基于自助法的结构学习算法，并将其应用于高斯贝叶斯网。算法分为三个步骤：

1)对观测样本重抽样得到B组Bootstrap样本；

2)利用结构学习算法,如PC算法、GES算法等，得到B个DAG，并求得B个DAG对应贝叶斯网的极大似然估计；

3)以B个DAG中出现的边作为候选边搜索一个DAG，使其对应的贝叶斯网的极大似然估计与B个极大似然估计的惩罚KL距离的平均值最小。

文中算法与Wang 等[11]最主要的区别在于，利用惩罚的KL距离作为聚合准则。KL距离比SHD有更好的性质，例如对于两个等价的DAG，它们对应模型的极大似然估计是相同的，因而这两个极大似然估计到B个极大似然估计的惩罚KL距离相同，但是SHD却不具备这一性质。

1 高斯贝叶斯网

贝叶斯网结构由有向无圈图G(V,E)表示。顶点集V={1,2，…,p}表示随机向量X=(X1,X2，…,Xp)。边集E={(i,j)∈V×V:i→j}, 其中i→j表示图G中的有向边。给定图G的结构, 随机向量X=(X1,X2,…,Xp)的联合概率密度函数可以分解为

给定一个联合分布，就可能存在多种分解形式，从而得到不同的DAG。所有蕴含相同条件独立关系的DAG构成一个等价类，同一等价类中的DAG具有相同的骨架和v结构。每个等价类都可以由完全部分有向无圈图(CPDAG)来表示。

当联合分布P为多元高斯分布时，高斯贝叶斯网可根据密度函数的分解写成结构方程模型的形式。

j=1,2,…,p，

X=v+ATX+E,

其中

v=(v1,v2,…,vp)T，

E=(ε1,ε2,…,εp)～N(0,D)，

A=(aij)是邻接矩阵,Aii=0。以I表示p×p维单位矩阵，通过简单的矩阵变换有

X=(I-AT)-1v+(I-AT)-1E

由E～N(0,D)及正态分布的性质，可得X～N(μ,Σ)，其中

μ=(I-AT)-1ν,

Σ=(I-AT)-1D(I-A)-1,

这里

|I-A|=1，

考虑在给定样本的情况下，如何估计μ、A和D。

令x(1),x(2),…,x(n)为多元高斯分布N(μ,Σ)的n个观测值，其中

x(i)=(xi1,xi2,…,xip)T。

样本均值

样本协方差阵

则有对数似然函数

这里

Σ=(I-AT)-1D(I-A)-1，

于是有

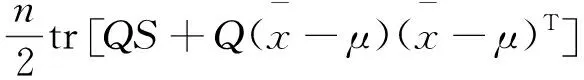
式中：Q=(I-A)D-1(I-A)T。

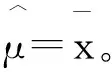
2 基于Bootstrap和KL距离的结构学习

许多贝叶斯网结构学习算法不具有稳健性，即使是较小的数据扰动，都可能导致得到的DAG有较大变化。为此，Wang 等[10]提出了自助聚合(Bootstrap aggregating)方法，以得到更稳定的图结构。这种方法可以在一定程度上避免过拟合，并减小学习算法的假边发现率。它们的算法称为DAGBag，详细过程见表1。

表1 算法1. DAGBag

上述DAGBag算法以DAG之间的结构海明距离(SHD)为度量，旨在寻找一个与集合Ge:={G1,G2,…,GB}中所有DAG的平均距离最小的有向无圈图G*。但是这种采用SHD为度量的方法不足以区分每一个DAG，原因在于：等价的DAG可能得到不同的scored(G:Ge)，而不同等价类中的DAG也可能得到相同的scored(G:Ge)。

为避免这个问题，以Kullback-Leibler(KL)[11]距离作为度量。两个概率密度函数f(x)和g(x)之间的KL距离定义为

对于正态分布N(μ1,Σ1),N(μ2,Σ2)，其KL距离为

当μ1=μ2时，有

从而有

式中：C0----与样本协方差阵S有关的量。

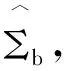
表2 算法2. 基于KL距离的Bootstrap学习DAG

选取KL距离作为度量，是因为：

1)可以更精确地度量分布间的距离。

以及正定矩阵Σ，有

其中

式中：n----样本量;

df----模型中自由参数的个数，也就是邻接矩阵A中的非零元素个数。

表3 算法3. 基于Bootstrap的惩罚KL距离学习DAG

在算法3中，有以下几点需要说明。首先，针对算法c)中的优化问题

采用类似于GDS的搜索策略。由于DAG数量随变量数呈超指数增长，一般无法遍历搜索,以求得上式的最小值，因此,借鉴基于道义图的方法GDSM思想，利用已得到的Ge:={G1,G2,…,GB}信息，以缩小DAG骨架的搜索范围。具体对于任意一对顶点i和j，计算有向边i→j在Ge中出现的频率fij。给定一个阈值f，令骨架边集候选集合为{i→j|fij≥f}。也就是说，只有频率大于阈值的边才可能作为DAG中的边。阈值f根据不同的结构学习算法L采用不同的值。文中模拟中，如果用GES算法作为L，则选的阈值为f≤0.70。若PC算法作为L，一般f≤0.30。

进行贪婪DAG搜索时，考虑两种初值的方式：

1)根据fij对所有的有向边i→j由大到小排序，然后从空的DAG(即没有边的DAG)出发，按边的频率由大到小依次向DAG中添加边，使DAG中的边尽量与{i→j|fij≥f}一致，并且保证得到的图仍然是一个有向无圈图，该初值称为最多边DAG；

2)从Ge:={G1,G2,…,GB}中随机选一个图，该初值称为随机DAG。

为了避免贪婪搜索陷入局部极值，将重复5次贪婪搜索过程，选择一个得分最好的结果作为最终结果。

3 模拟实验

通过模拟来比较BPKL算法、GDS算法、基于道义图的GDSM算法、PC算法和GES算法。

在BPKL算法中，a)重抽样次数设置为B=200;b)结构学习算法L采用GES算法和PC算法;c)搜索过程中，骨架候选边频率的阈值，对于GES算法，选为f=10%,30%,50%,70%,90%，而对于PC算法，选为f=1%,5%,10%,30%。搜索的初值采用上节所述的两种方式。如果结构学习算法采用GES，f=10%，初值为最多边DAG，则算法记为gesb10; 如果初值选为随机DAG，则算法记为gesbR10;如果结构学习算法采用PC，f=5%，初值为最多边DAG，则算法记为pcb5; 如果初值选为随机DAG，则算法记为pcbR5。以此类推。

基于该模型产生样本量为n的模拟数据，并采用以上各种方法进行结构学习。其中BPKL方法和GDS、GDSM是在DAG的空间中搜索的，因而得到一个DAG；而GES和PC将得到CPDAG，用于表示马尔可夫等价。为了比较公平性，将前三种方法得到的DAG转换成CPDAG。从而将它们的CPDAG求与真实模型的CPDAG之间的结构海明距离。所谓结构海明距离，也就是相对于真实的CPDAG错误边数，包括多出的边数(ee)、缺少的边数(me)、反向的边数(rd)、少方向的边数(md,也就是真实情况为有向边，但算法得到的CPDAG中为无向边数)、多方向的边数(ed,也就是真实情况为无向边，但算法得到的CPDAG中为有向边)。

对顶点数p=20, 样本量n=100的情况进行100次模拟，并利用箱线图和柱状图比较各种算法估计出的模型与真模型之间的结构海明距离，以及各类错误边数的平均值。模拟结果分别如图1和图2所示。

图1给出24种算法的SHD箱线图。可以看到，在BPKL中无论采用GES算法还是PC算法，得到CPDAG的结构海明距离均明显小于传统GES和PC算法的结构海明距离。当阈值f较小时，与真实图的结构海明距离也较小，例如gesb10、gesbR10和pcb10、pcbR10。而随机的DAG初值，对阈值f的选取依赖更小一些。

图2给出24种算法的柱状图，其中横轴表示24种算法，纵轴rd-me-md-ee-ed代表在100次模拟中五种错误边出现次数的均值。在CPDAG的比较结果中，GDS、GDSM、GES算法的ee最多，PC算法的me最多。在BPKL中，由于在c)中限制了骨架的搜索范围必须出现在B个DAG中，并且设置了候选边的阈值f，因而无论是选用ges，还是选用PC，me的错误都增大了一些，特别是对于gesb90，要求候选边必须出现超过90%的频率，导致me相对较大。但是这样的策略，可以大大降低ee、rd、ed错误，从而使整体结构海明距离变小。整体来说，gesb10和gesbR10表现最好。

其他条件下的模拟结果与其类似，因篇幅有限，文中不再给出。需要指出的是,随着顶点数p的增加，SHD的整体水平会增加，随着样本量n的增加，SHD的整体水平会略微降低。此外，还模拟了B=50,100的情况。我们发现，B=50或100时,BPKL的表现并不比B=200时差，很难说明B取哪个最优。

4 实例分析

利用高斯贝叶斯网建立拟南芥(Arabidopsis thaliana)基因的关系，该数据含有39个基因的118个基因芯片(Affymetrix)微阵列数据。Wille等[13]曾利用高斯图模型刻画基因间的关系。先对变量进行正态变换和标准化，以消除各变量之间不同量纲对结果的影响。然后用模拟分析中的算法对处理后的数据进行建模。

文中仅展示gesb10、gesbR10、pcb1和pcbR1算法对真实数据的估计结果。通过这4种算法得到的邻接矩阵(见图1)可以看到，gesb10和gesbR10的估计结果相近，pcb1和pcbR1的结果相差很小，而pcb1和pcbR1的估计结果明显稀疏。图2给出了这4种算法同时估计出来的边所构成的邻接矩阵，其中横坐标和纵坐标代表着每种基因的名字。为使估计结果更具有可信度，选择图2中邻接矩阵所对应的模型作为最终的估计结果，如图3所示。

共同的邻接矩阵如图4所示。

最终估计图模型如图5所示。

5 结 语

给出了贝叶斯网结构学习的新算法BPKL。该方法基于自助法，并利用KL距离衡量最优模型到B个DAG的平均距离。通过对不同情况的模拟，发现自助法样本量B=50,100,200时，BPKL都有良好的表现。当候选边的阈值f较小时，虽然计算时间稍微增加，但结构学习的效果会好很多，可以有效地降低SHD。文中只讨论了高斯贝叶斯网的结构学习问题,对于离散变量的贝叶斯网和混变量的贝叶斯网依然适用,而且已经进行了初步尝试，取得了不错的模拟结果[14]。