基于温度场分析的安注管线止逆阀内漏监测方法研究

董晓梅，董俊华，余雏麟，高炳军

(河北工业大学 化工学院，天津 300130)

全球许多核电厂报告的事件表明，管道中的热分层会导致管道材料产生过度的热应力和疲劳，可能导致严重的热疲劳开裂和管道系统的泄漏事故[1]。尽管如此，老式核电站的设计并没有考虑这种热效应[2]。导致意外热疲劳的热分层现象是由冷热流体之间的密度差异产生的[3，4]。一种典型的热分层常发生在连接到反应堆冷却系统(RCS)的安全注入系统(RIS)中，是由于RCS向安注管线的湍流渗入以及支管止逆阀内漏造成的[5，6]。安全注入系统仅在核电厂发生事故时向核反应堆供应应急水冷却时才运行，在正常工作状态下，由于RIS中的所有阀门都关闭，RIS的冷却剂是隔离的。但是，如果连接硼水箱和一回路主管道支管的阀门可能会出现微量的渗漏，冷水将进人高温水侧的管道[7]，并在一定范围内形成热分层。泄漏流量的准确确定对于安注管线的热疲劳分析至关重要，而由于核管道安注管线流体流动的特殊性，对于存在冷热流体热分层、湍流渗入、冷热交替等复杂流体流动与传热现象的问题，目前尚缺乏有效的泄漏监测手段。本研究中，通过流固耦合计算分析评估在RIS管线内漏条件下的热分层特征，提取止逆阀阀前管道外壁温度并定义热分层特征温度参数，得出该特征温度参数与泄漏量的定量关系式。 在此，仅以热安注管线为例进行分析讨论。

1 数值计算模型

1.1 物理模型

一回路热段管内径为736.6 mm，壁厚为67 mm，长度为4 904 mm，水平放置。安注管内径为131.78 mm，壁厚为18.26 mm，通过管嘴与水平面呈30°和主管道热段连接，其上安装有止逆阀。利用SolidWorks建立含有主管道热段和安注管的几何模型，支管末端阀门泄漏的区域是研究的重点，在阀门中建立月牙形的开孔模拟阀门泄漏，如图1所示，其中阀门开度与泄漏流速的关系由公式(1)表示[8]。

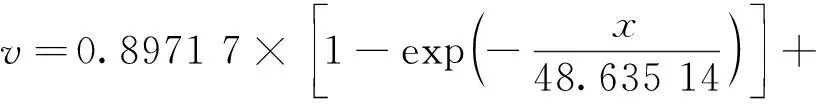
(1)

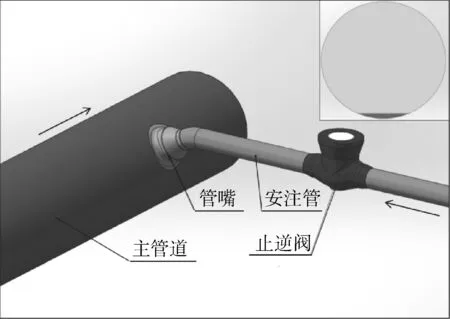
图1 几何模型Fig.1 Geometric model

式中：v——泄漏流体速度，m/s；

x——阀门开度。

1.2 网格划分与质量检查

用ANSYS ICEM划分流体域和固体域的网格，流体域和固体域网格导入Fluent进行流场、温度场计算。止逆阀和止逆阀内的流体域使用四面体划分非结构网格，其他流体域和固体域均采用六面体网格，划分结构化网格。为了尽可能真实地模拟流体混合过程，本文对网格模型进行了网格无关性验证，计算时，先对模型进行初步网格划分，在此基础上，对网格进行加密，直到网格的大小对计算结果影响忽略不计时，才最终的确立网格大小和分布。网格Quality质量低于0.2的网格处在结构和非结构网格的交界面处，对流场和温度场影响较小。最终网格如图2所示，网格的数量为75万个，已具有良好的网格无关性。

图2 网格模型Fig.2 Meshof the model

1.3 计算方法

采用三维全尺寸稳态流固耦合传热的计算流体动力学(CFD)方法对安注管线发生热分层现象时的流动与传热进行数值研究。与以往的k-ε湍流模型相比，将计算控制区域扩展到安注管管壁所在的固体区域，采用更适合于求解具有流动分离情况的剪切应力传输模型Transition SST湍流模型[9]。选择三维、双精度、基于压力隐式求解器，求解控制方程包括连续性方程，质量、能量守恒方程及湍流输运方程。并将密度处理为温度的线性函数来估算浮力项的影响。

1.3.1 控制方程

(1)全浮力模型

管内流体温差较大，且工作在高温、高压下，密度随温度的变化明显。因此，本文采用全浮力模型进行计算。在包括浮力的计算中，动量方程需增加1个源项[10]。全浮力模型则根据求解的实际密度通过公式(2)直接对浮力进行评估，进而求解全场浮力。

SM,buoy=(ρ-ρref)g

(2)

式中：SM,buoy——浮力源项，N；

ρ——密度，kg/m3；

ρref——参考密度，kg/m3；

g——重力加速度，m/s2。

(2)连续性方程

(3)

式中：t——时间，s；

xj(j=1，2，3)——直角坐标分量，m；

uj(j=1，2，3)——速度分量，m/s。

(3)动量守恒方程

(4)

(5)

式中：μ——黏性系数，kg/(m·s)；

p——压力，Pa；

(4)能量守恒方程

(6)

式中：cp——比定压热容，J/(kg·K)；

λ——导热系数，W/(m·K)；

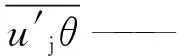
S——能量方程的源项。

(5)k和ω输运方程

(7)

(8)

式中：Gk，Gω——名义速度梯度下k的产生项，ω产生项；

Γk，Γω——k和ω的有效扩散率；

Yk，Yω——k和ω的有效耗散率；

Sk，Sω——用户自定义源项。

Transition SST数学方程模型在k-ωSST 的基础上额外增加了两个输运方程，分别是间歇度γ和瞬态起始标准，可表示为：

(9)

(10)

有效扩散率Γk和Γω可表示为

(11)

式中：σk和σω——k和ω的湍流普朗特数；

μt——湍流黏度。

(12)

式中：ɑ*可在低雷诺数时限制湍流粘度的大小，ɑ*的定义如下：

(13)

(14)

1.3.2 边界条件

由于主管和热安注管外侧都有保温层，所以主管道和热安注管的外壁设为绝热边界。忽略管道端部横截面传热量，因此也设为绝热边界。流体域和固体域的交界面设为耦合壁面边界条件。

热安注管进口设为速度进口边界；主管道的流量按功率运行时的流量确定，主管道进口也设为速度入口边界条件；压力出口，压强为15.5 MPa。为了避免进口段对混合过程模拟的影响，消除边界条件对流场的干扰，同时减小计算量，通过fluent的二次开发UDF，采用DEFINE_ PROFILE编写，将发展完全后的速度分布添加到主、支管的进口边界条件中。

1.3.3 物性参数

本文通过自定义材料方式实现材料参数的定义，热安注管和主管材料为Z2 CN 18-10，假定流体为不可压缩流体，物性参数采用变物性。金属材料属性取自RCC-M规范[11]，对于流体的物理性质，使用基于技术数据中的物性数据将相关性作为温度的函数进行计算，材料属性随温度变化规律如表1所示。

表1 材料参数表Table 1 Material parameters

1.3.4 模型验证

为了验证计算模型的准确性，利用本文的数值计算方法来模拟Nobuo Nakamori试验工况[12]。得到水平支管某剖面上竖直方向高度H与温度分布的无量纲关系的模拟数据与试验数据对比结果如图 3 所示，模拟温度与试验数据较好吻合，相对误差小于 2%，表明本文所采用的数值计算方法的准确性。图3中D为支管直径；T为剖面上某点的温度；Tmin为剖面上的最低温度；Tmax为剖面上的最高温度。

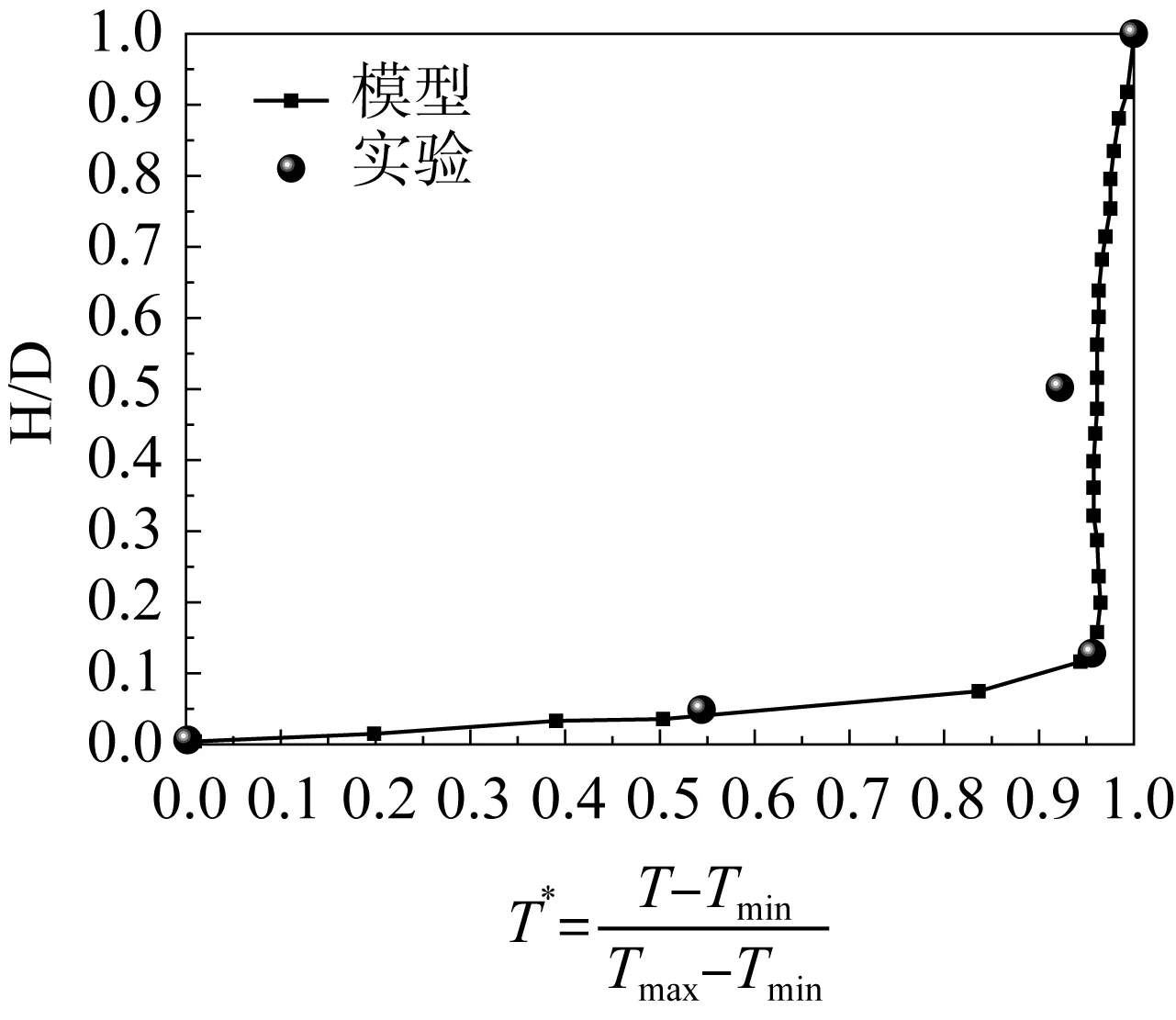
图3 某剖面高度与温度分布的无量纲关系Fig.3 No-dimensional relation of temperature and Height in section plane

2 计算方案与结果分析

2.1 计算方案

核电厂主管道内热水参数受用电负荷影响，是不稳定的。根据阀前主管道流体温度Thot、流量Qhot及阀后管内泄漏工质的温度Tcold范围，主管道内热流体温度Thot取564～601 K；流量Qhot范围为90%～ 110 %Q额(Q额=2.379×107L/h)；安注管泄漏的冷流体温度Tcold范围为293～328 K；泄漏量QLeak取5～400 L/h。得出不同工况下的温度场并获取阀前监测位置管外壁温度数据，每一个工况对应一个监测位置的管壁温度分布。采用单一因子变量法着重分析和探讨了一回路主管道与安注管工质参数是如何影响止逆阀前管外壁温度的。依据数学建模方法，采用非线性回归模型建立管外壁温度与影响因素之间的函数关系式。

2.2 计算结果与分析

Thot=599.15 K、Qhot=2.379×107L/h、Tcold=327.15 K、QLeak=400 L/h工况下管外壁温度分布云图如图4 (a)所示，可见近主管道区域受湍流渗入的影响管外壁温度均匀，而靠近阀门较大的区域内由于流体热分层管壁温度上下存在温差。不同圆周位置上管外壁温度沿管长的变化如图4(b)所示，可见管外壁温度自主管道开始沿管长都呈下降趋势，但湍流渗入区圆周方向无明显温差，热分层区有温差，较大范围内温差分布规律相似。

图4 管外壁温度分布Fig.4 Temperature distribution of the pipe outer surface

不同泄漏流量下阀前50 mm位置横截面流体与管壁的温度云图如图5所示。由图可见在所讨论的泄漏流量范围内流体均存在较为明显的热分层现象。上部温度较高，下部温度较低，最高温度在最上部，最低温度在最下部。管壁受分层流体的作用，也呈现相应的温度变化，即上部温度高下部温度低，最高温度在最上部，最低温度在最下部。

图5 不同泄漏流量下截面温度分布Fig.5 Temperature distribution of cross section under different leakage flow rates

图6为截面直径线位置温度分布曲线，最高最低位置金属管壁内外温差很小。直径线位置流体温度从高到低是逐渐变低的，热分层是渐变的，这是由于流体沿垂直方向的扩散与热传导造成的。管壁与流体最高最低点温差均随泄漏流量增加而增大，泄漏流量为400 L/h时，最大温差达到105 ℃。

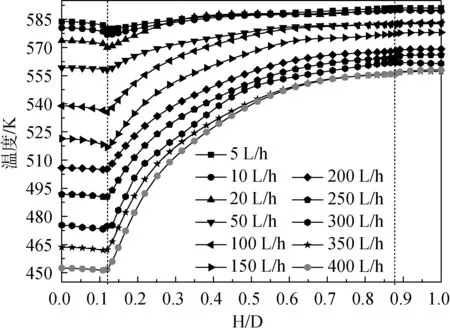
图6 截面直径线上温度分布Fig.6 Vertical temperature distribution of Cross Section

不同泄漏流量时，阀前50 mm管外壁面沿圆周方向温度分布如图7所示，温度分布左右基本对称，QLeak越大，管外壁温度越低。

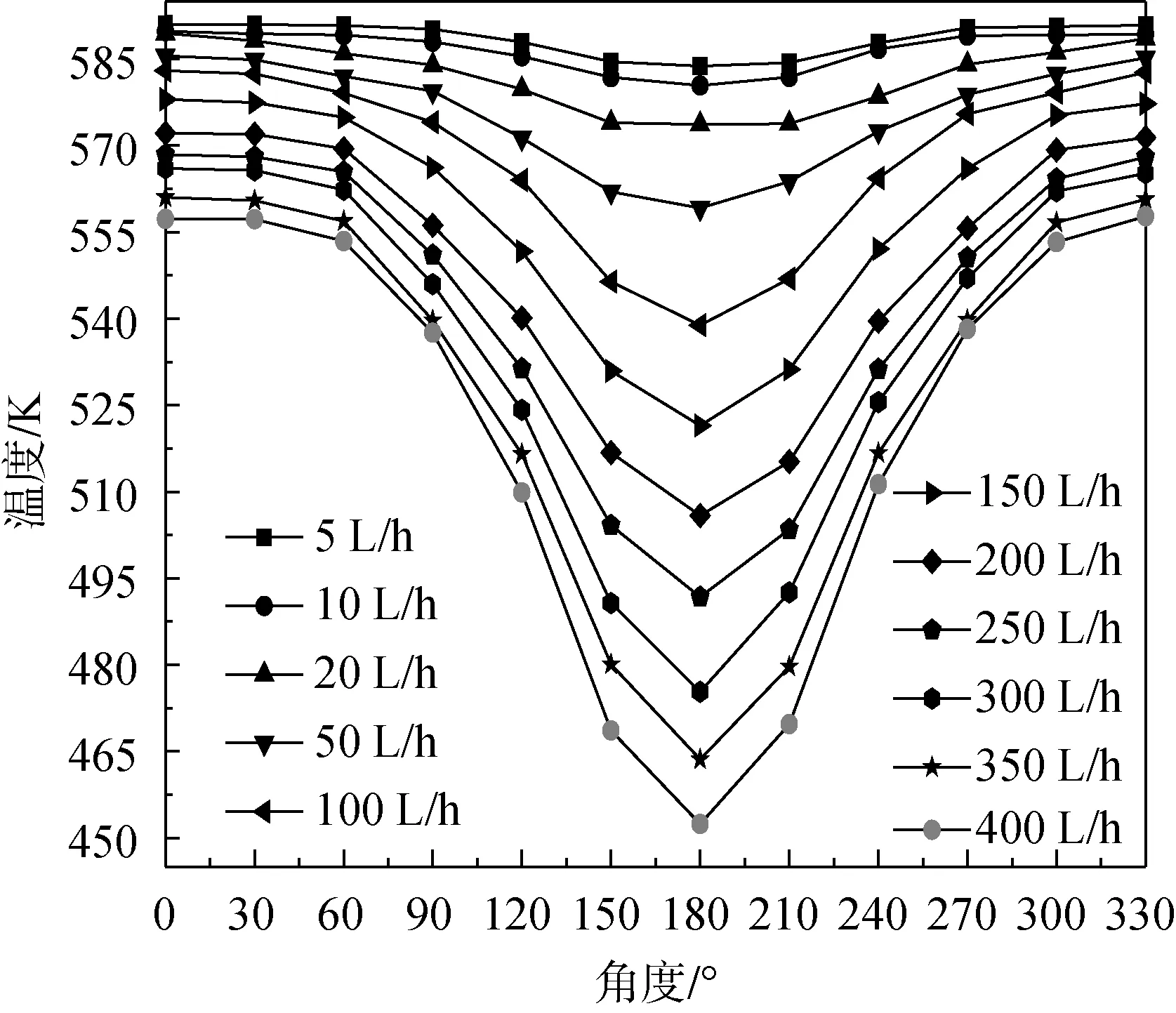
图7 不同泄漏量下管外壁温度分布Fig.7 Pipe wall temperatures at various leakage rate

3 泄漏预测模型的建立

3.1 热分层特征温度参数

将温度监测点设在止逆阀前50 mm处的位置AT6B—7，在测量位置的一侧沿圆周方向30°等间距安装7个热电偶，如图8所示。根据7个测点温度可整理如下热分层温度特征参数。

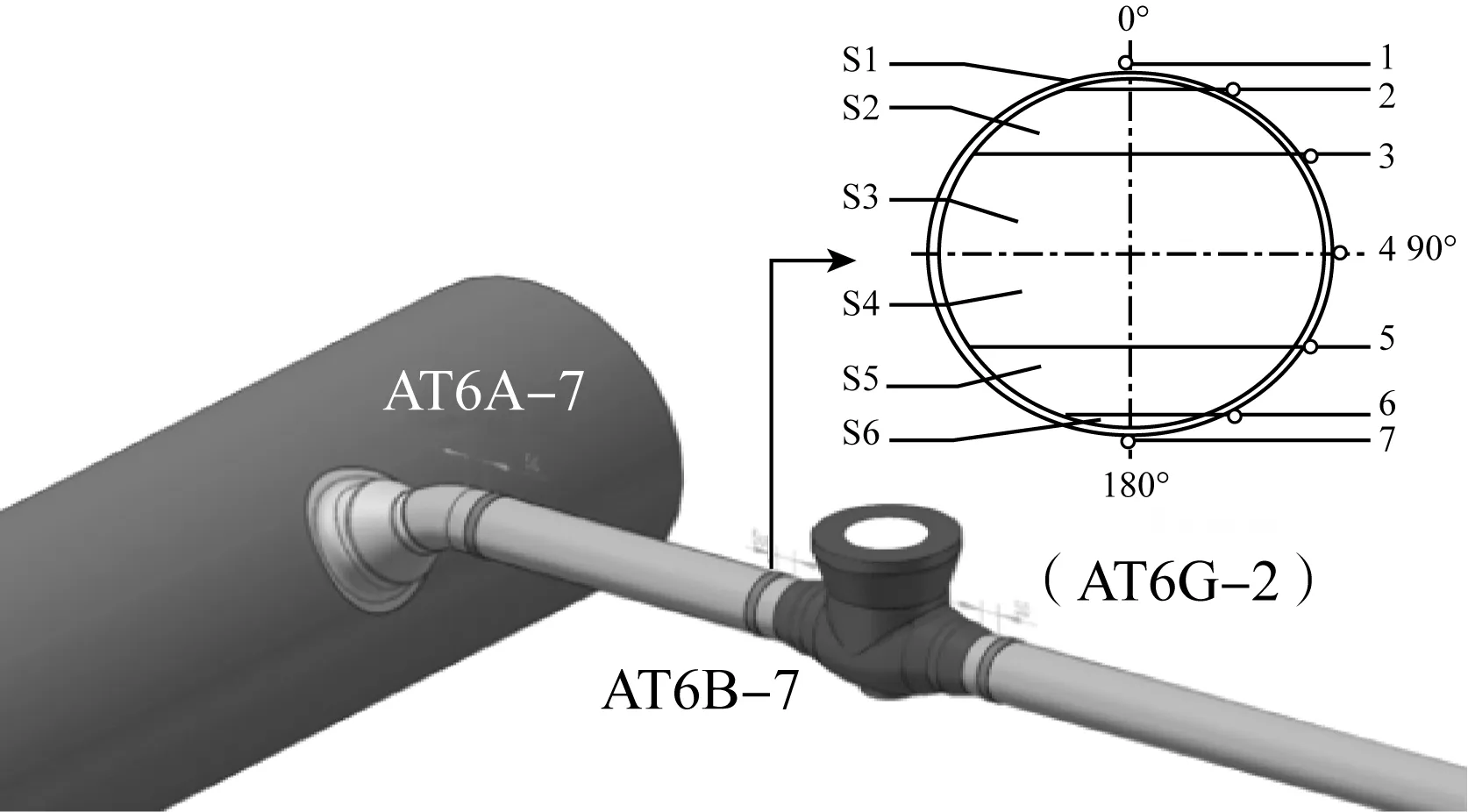
图8 温度测点的布置Fig.8 Arrangement of temperature measuring points

令

(15)

(16)

(17)

(18)

(19)

(20)

则热分层致温差为

ΔT=T0°-T180°

(21)

热分层致当量面平均温度为

(22)

(23)

式中：Si——两相邻测温点间监测截面的面积。

3.2 热分层特征温度参数单变量分析

热分层特征温度参数随主管道流体温度的变化关系如图9所示，当量面平均温度TA随着主管道流体温度的增加而增加，且呈线性增加趋势。这是因为主管道内流体的温度越高，则管壁温度会直接增大，热流体的传热速率加快，热流密度的增加从而管壁的温度相应的增加。主管道温度增大时，管外壁的温差ΔT逐渐增大，呈非线性，运用最小二乘法进行拟合时，管壁温差ΔT与主管道温度成三次关系。

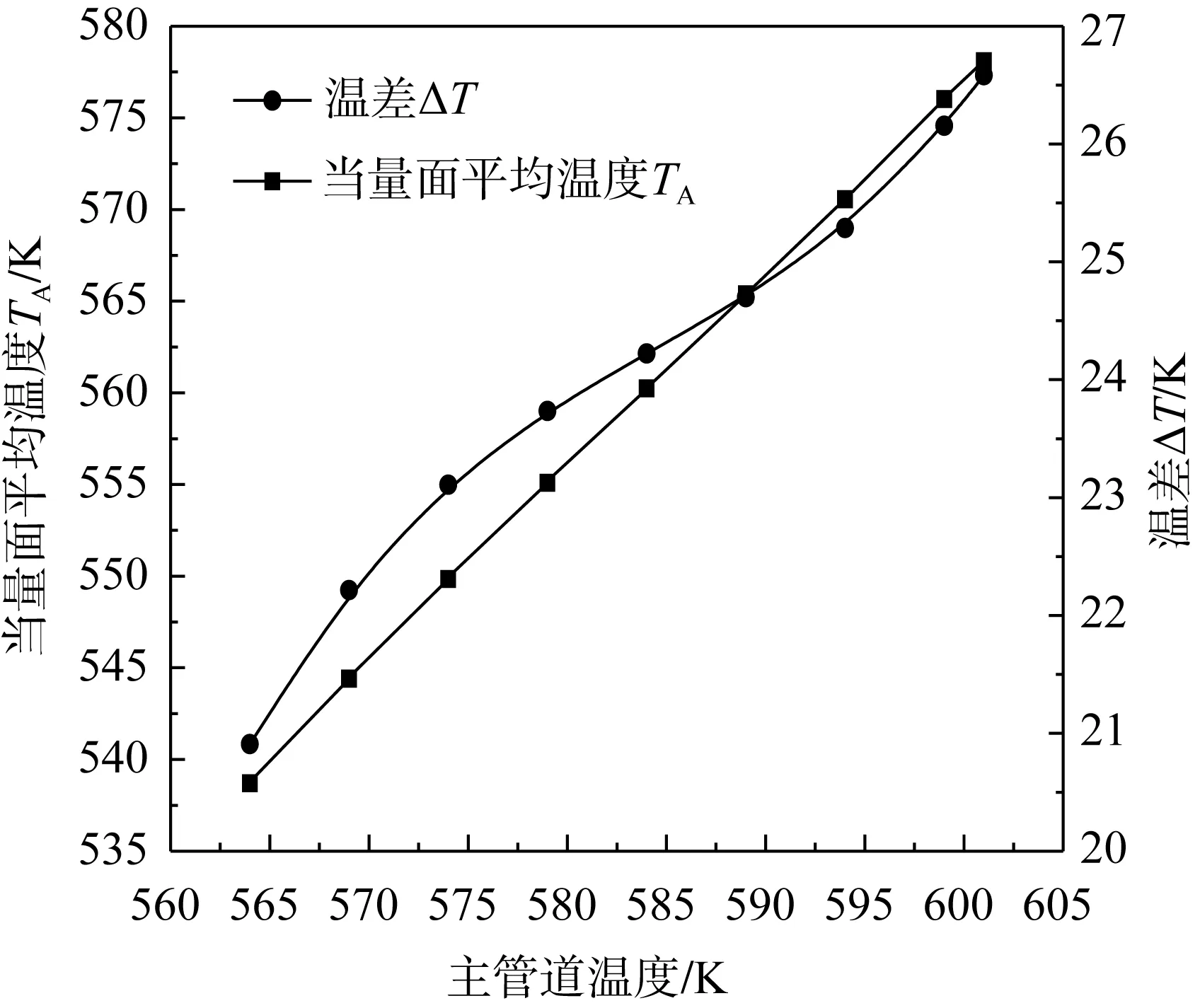
图9 温度特征值随主管道温度变化关系Fig.9 Variation relationship of characteristic temperature with the main pipe temperature

热分层特征温度参数随主管道流量的变化关系如图10所示，当主管道内流量逐渐增大时，当量面平均温度TA呈非线性降低，运用最小二乘法进行拟合时，当量平均温度TA与主管道流量成幂函数关系。主管道流量增大时，温差ΔT非线性降低，运用最小二乘法进行拟合时，温差ΔT与主管道流量成一阶指数衰减函数关系。

图10 温度特征值随主管道流量变化关系Fig.10 Variation relationship of characteristic temperature with the main pipe flow rate

热分层特征温度参数随泄漏流体温度的变化关系如图11所示，当泄漏工质温度逐渐增大时，当量面平均温度TA线性增加。管道泄漏工质温度增大时，管壁温差ΔT线性降低。

图11 温度特征值随泄漏工质温度变化关系Fig.11 Variation relationship of characteristic temperature with the leakage flow temperature

热分层特征温度参数随泄漏流量的变化关系如图12所示，当泄漏工质流量逐渐增大时，监测位置的当量面平均温度TA有明显的减小趋势，且成二次函数关系。当管道泄漏流体的流量增大时，管壁温差ΔT非线性增大。运用最小二乘法进行拟合时，温差ΔT与泄漏流量成二次关系。

图12 温度特征值随泄漏量变化关系Fig.12 Variation relationship of characteristic temperature with the leakage flow rate

3.3 热分层特征温度参数多变量拟合

根据不同工况条件进行的流固耦合计算结果，利用MATLAB统计工具箱中的regress命令，对热分层特征温度参数关于主管道内流体温度Thot、主管道内流体流速Qhot、安注流体温度Tcold、泄漏流量QLeak进行多变量回归计算可得

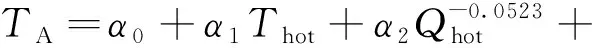
(24)

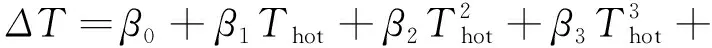
(25)

式中：α0……α5，β0……β7——系数。

TA和ΔT统计计算的R2分别为0.9967和0.9957，表明所定义的热分层特征温度参数与回归变量之间有良好的相关性。

从而可建立内漏流量QLeak的阀门内漏量化预测模型

QLeak,TA=g(Thot,Qhot,Tcold,TA)

(26)

QLeak,ΔT=f(Thot,Qhot,Tcold,ΔT)

(27)

现场泄漏流量计算时，通过现场在阀前管外壁布置的热电偶，得到测温点处的温度，根据公式(15)～公式(23)计算出所述测温点的当量面平均温度TA测，将TA测代入到公式(26)中，得到QLeak,TA，根据公式(21)计算出所述测温点的温度差ΔT测，将ΔT测代入到公式(27)中，得到QLeak,ΔT，若满足公式(28)，那么取它们两个的算数平均值如公式(29)所示，若不满足，则取两个之间的较大值如公式(30)所示。

(28)

(29)

QLeak=max{QLeak,TA,QLeak,ΔT}

(30)

3.4 误差分析

拟合关联式结果与数值计算结果吻合较好，最大误差为6.471 7%，可满足工程阀门内泄漏流量需要。

4 结论

以热安注管线止逆阀泄漏为例，探讨了基于阀前管壁温度场测量的阀内泄漏流量监测方法。通过流固耦合计算对热安注管线由于阀门内泄漏造成的热分层现象进行了详细分析，定义了阀前监测截面管外热分层特征温度参数，通过多变量回归计算获取了热分层特征温度参数与主管道内流体温度Thot、主管道内流体流速Qhot、泄漏流体温度Tcold和泄漏流量QLeak之间的关系式。只要根据阀前监测截面管外壁7点监测温度获取热分层特征温度参数，即可根据电厂已知参数(主管道内流体温度Thot、主管道内流体流速Qhot、泄漏流体温度Tcold)较为准确地预测止逆阀的泄漏流量。