基于MOP模型的新能源汽车电池回收网点选址研究

刘 娟， 兰建义

(河南理工大学 能源科学与工程学院， 河南 焦作 454003)

随着科技的发展和环保的要求，新能源汽车逐渐成为新的运输工具，在运输行业占据着重要的地位。相较于传统汽车，新能源汽车的使用能够有效地改善空气质量，降低能源损耗，更符合当下的环保要求。然而随着新能源汽车数量的不断增加，其报废回收问题日渐突出，动力电池由于其特殊性，回收问题尤为突出。据汽车工业协会统计，近10年间，我国新能源汽车的产销数量不断增加，如图1、图2。

图1 2011-2018年新能源汽车产销量 单位：辆

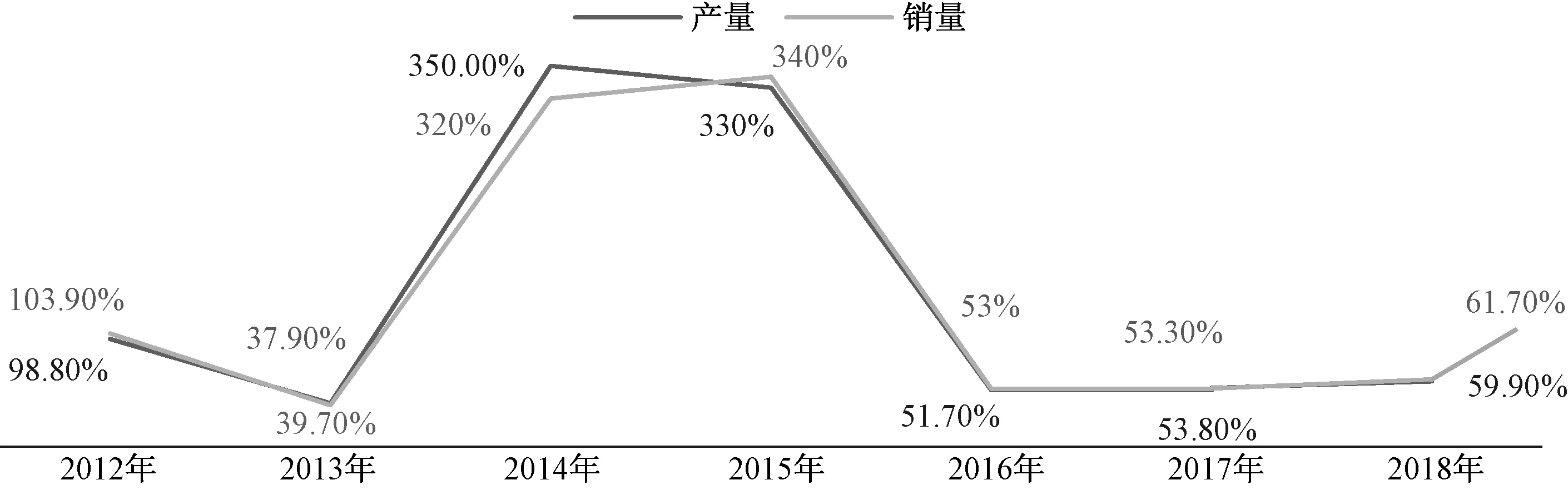
图2 2012-2018年新能源汽车产销量同比增长率 单位：%

由图可以看出新能源汽车的数量呈上升趋势，2016年前，产销量的同比增长率是呈大幅度波动，在2016年之后，恢复稳定增长，随着新能源汽车规划的完善，今后几年我国新能源汽车产销依然呈现增长趋势。而根据相关资料显示，动力电池的使用年限一般是5～6年，意味着从2018开始，我国有大批量的电池进入退役期，汽车电池的回收问题成为新能源汽车的回收焦点。针对这一形势，国家出台了相应的政策，从2018年9月30日国家开始公布新能源汽车动力蓄电池回收服务网点信息，规范回收，着手试点回收，鼓励建立回收网点，信息每季度都进行更新。但是，由于这些动力蓄电池回收服务网点的位置受所属企业的位置约束，对电池回收成本和效率影响较大，因此，加强对动力电池回收网点选址的统一规划，进行全局优化，将会极大地提高回收网点的回收效果。同时，优化回收网点布局也会得到较大的经济效益和社会效益，进一步提高回收机构的回收积极性。

对于回收网点的研究，目前国内网点选址布局优化的相关资料并不多，而对新能源电池回收网点的选址研究文献更少。而在最新的相关研究过程中，围绕网点的选址问题进行研究的方法很多，罗宜美研究再制造逆向物流网络设施的选址问题中运用多目标规划模型来求解[1]。高桃丽在固体废物处理站布局的研究中，将多目标规划模型与最小偏差法相结合,用LINGO求得最满意解[2]。李明明利用主要目标法和贪婪取走启发式算法研究废弃物回收网点选址并建立了规划模型，使得废物回收O2O行业相应服务最大化，成本最小化[3]。贺政纲将禁忌算法和遗传算法相结合弥补彼此搜索的不足，并将此法用在报废汽车物流的路径优化中，建立模型最后求出相应的最优布局节点和回收路线[4]。狄卫民在研究废旧家电回收站选址的问题中采用多目标规划模型及满意优化理论相结合的方法，最后结合实例进行分析，验证了方法的可行性[5]。贾月恬在研究电动汽车的充电站选址中使用了多目标规划模型，其研究的是动态网络，且在建立模型时区别于静态模型将目标变成了两个，又加入时间因素使得模型具有记忆功能，最后运用遗传算法进行求解[6]。谢华忠对加油站的选址进行研究时，运用层次分析法将定性定量影响因素分成若干层，然后加以计算确定对应权重，最后建立层次目标模型，使问题归结为最高层的相对重要权值的确定或排定[7]。李明在研究物流配送中心选址问题中，对一般的线性规划问题进行改进，然后建立非线性混合0-1规划模型，运用LINGO来求解，在获得最优成本的同时也确定了建设物流中心的数量[8]。Banu Soylu研究机场选址中提出了双目标分配p-pub中值问题，讨论帕累托边界的性质，并提出了寻找帕累托边界的精确启发式算法，并利用实例进行验证[9]。生力军深入分析物流配送中心选址时建立数学模型，用量子粒子群求解，有效避免了经典粒子群早熟收敛和局部最优[10]。高建树在机场充电桩分布的研究中选用遗传算法建立模型求解，对其参数进行标定，提升种群的多样性和全局优化的能力，结合实例进行仿真分析，确定其方法的可行性和有效性[11]。郭福利对河南省快递网络节点选址中，从“点——线——面”等不同的角度进行分析研究，建立数学模型运用软件进行求解[12]。张金光在城市公园选址中，根据可达性的分布和众多现实因素,借助地理信息系统(GIS)平台的网络分析模型，选得公园位置最优[13]。郑长江在优化物流配送中心位置中引入Voronoi 图，将其与改进后的P-中值模型相结合，用Matlab来求出整个系统的节点最优布局[14]。朱莉在研究应急物资选址中构建数学模型，对关键性参数进行敏感分析，并用遗传算法结合实例仿真求解[15]。

本文结合实际情况对新能源汽车电池回收网点选址进行研究，利用多目标规划模型进行选址优化，将成本和回收率作为优化目标，使用LINGO和其他数学方法进行求解，求解快速、节省时间,而且模型灵活易调整，目的是在最小成本和回收率最大的条件下，在众多的备选网点中选出最满意的回收网点，并确定对应的回收网点数量、位置、半径、回收率及回收运输情况。

1 基于MOP模型的新能源电池回收网点选址模型建立

1.1 多目标规划模型

多目标规划是数学规划的一个分支，主要研究两个或两个以上目标函数在给定区域上的最优化，又称多目标最优化,缩写为MOP。多目标规划的概念是1961年由美国数学家查尔斯和库柏首先提出，而多目标最优化思想，是在1896年由法国经济学家V.帕雷托提出。求解多目标规划的方法大体上有以下几种：一种是化多为少，即将多目标化为比较容易求解的单目标或双目标，如主要目标法、线性加权求和法、指数加权乘积法、理想点法等；另一种叫分层序列法，即将所有目标按其重要程度排序，先求得第一个目标最优解，在保证前一个目标最优解前提条件下求下一个没目标的最优解，一直到求得最后一个目标为止[16]。

多目标规划问题由两个基本部分组成;两个以上目标函数、若干约束条件。其模型一般形式如下：

min{f1(x),f2(x),…,fs(x)}

(1)

s.tgi(x)≤0,i=1,2,…,m

在(1)式中x=(x1,x2,…,xm)是决策变量，f1(x),f2(x),…,fs(x) 是决策目标[17]。

1.2 问题描述

现阶段新能源汽车电池的回收主要包括：二手商贩的回收、制造商回收、第三方回收，但在众多的回收机构中，有一部分机构不具备回收资格，回收途径也存在是违法行为。而现有的正规回收机构又比较少，导致了新能汽车电池回收成为制约新能源汽车发展的关键因素。在《电动汽车动力蓄电池回收利用技术政策(2015年版)》中鼓励多家企业通过委托代理或与回收企业、再生利用企业合作等形式，共建、共用废旧动力蓄电池回收网络，降低回收成本，提高回收网络运行效率。所以，本文通过制造企业多方联合、政府参与委托第三方进行回收并建立网点，从各个区域运回指定的回收网点进行回收。被回收网点覆盖点的区域回收率较高，所以通过网点覆盖面积来进行估算回收率具有一定的可行性。

1.3 模型的前提假设

为了使得模型具有操作性，在结合实际情况的基础上，对该模型作出以下假设：

1)回收电池的回收量均按其区域内新能源汽车保有量来统计，且与该区域内产品的消费成正比例关系。

2)单件物品所产生的运输费用与运输的距离成简单线性关系，为了便于计算，该模型运输距离近似按点与点之间的直线距离来计算。

3)所建设网点有容量限制，电池回收网点不存在环境影响评价争议，在运输过程中不存在运输污染。

4)产生回收电池的位置与数量已知，备选的新能源电池回收网点的位置已知。

5)一个产生回收电池的回收区域，只能运往一个回收网点。

6)网点覆盖区域内的电池全部有效回收。

1.4 多目标规划模型的建立

本文建立的模型，将成本费用和运输费用作为主要的求解目标，使得费用最小化，回收率最大化，将次要目标服务范围最大化作为约束条件，尽可能的覆盖目标区域，然后设置相应的约束条件，为了方便计算，模型将两个费用目标进行整合，使用主要目标法来确定模型的建立，完成后用LINGO软件进行求解。

由此建立的多目标规划模型如下，其主要目标是费用最小化：

Gj=(R-R0)×A

(2)

(3)

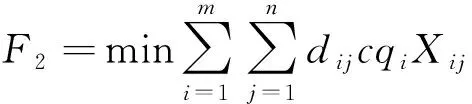
(4)

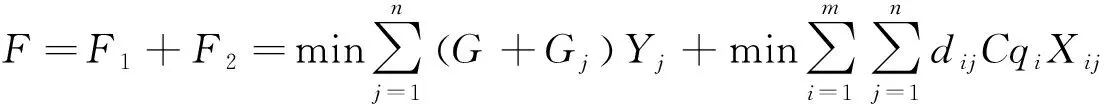
(5)

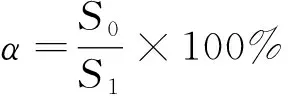
(6)

约束条件：0≤dij≤R；i=1,2,…,m.j=1,2,…,n.

(7)

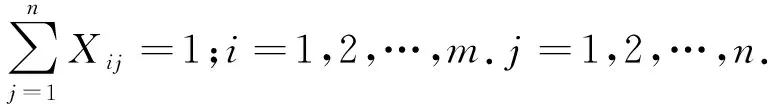
(8)

(9)

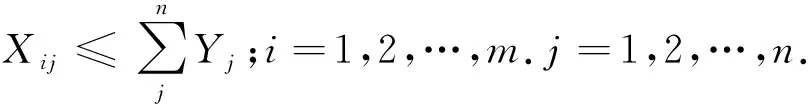
(10)

Xij∈{0,1}

(11)

Yj∈{0,1}

(12)

本模型中，所使用的符号所表示的含义如下：

R0：回收网点基本半径;

A：网点半径每增加一千米所产生的成本费用;

So：网点覆盖的总面积；

S1：规划区域总面积；

α：估算的回收率；

Gj：j处网点半径改变后产生的总费用;

G：单个回收网点建设的基本费用；

F1：回收网点建设的基本费用；

F2：回收网点j到产生回收电池区域i的运输费用；

E：回收网点的容量限制；

e：网点半径每增加一千米所增加的容量；

α：电池的回收率；

R：所建立的回收网点的服务半径；

I：产生回收电池位置的下标；

J：建立的回收网点的下标；

dij：产生回收电池点到回收网点的距离；

n：备选回收网点的数量；

m:产生回收物的地区的数量；

c:单件物品运输费用；

qi:回收电池产生点i所产生的回收电池数量；

Xij：二元变量，将产生i的物品指配给j,为1，否则为0；

Yj：回收网点j是否建立的变量，若开设值为1，不开设为0。

在确定基本模型建立后，在考虑到服务最大化和成本最小化，以及一些相关条件确定其约束条件为：(2)式为j处网点半径改变后产生的总费用；(3)式为网点建设的成本费用；(4)式为总运输费用；(5)式为所有费用的整合，费用最小化；(6)式为利用面积覆盖率估算的回收率；(7)式为网点要覆盖到产生点，尽可能的服务最大化；(8)式为一个产生报废电池的点只能运往一个回收网点；(9)式为每个回收网点的回收数量都不能超过容量限制；(10)式为只有建立了回收网点才可以回收动力电池；(11)式、(12)式为二元变量约束。

2 算例分析

现针对山西省某市一个区要围绕9个新能源汽车电池产生点建立电动汽车电池回收网点，经过实地走访和资料查阅，该区面积295平,其境内其备选的回收网点有7个，对应的单位运输费用为每公里10元，每个回收网点建设所需的基本费用50 000元，服务网点最基础的服务半径为4公里,回收容量限制是1 700个，随着半径的增大每千米会增加10 000元的成本，容量增加100个，该区域的相关数据收集如表1所示。

为了使得计算误差的缩小，所以在计算网点和产生点之间的距离时利用excel求解实际距离，而不是采用直线距离，且保留两位小数，详细数据如表3所示。

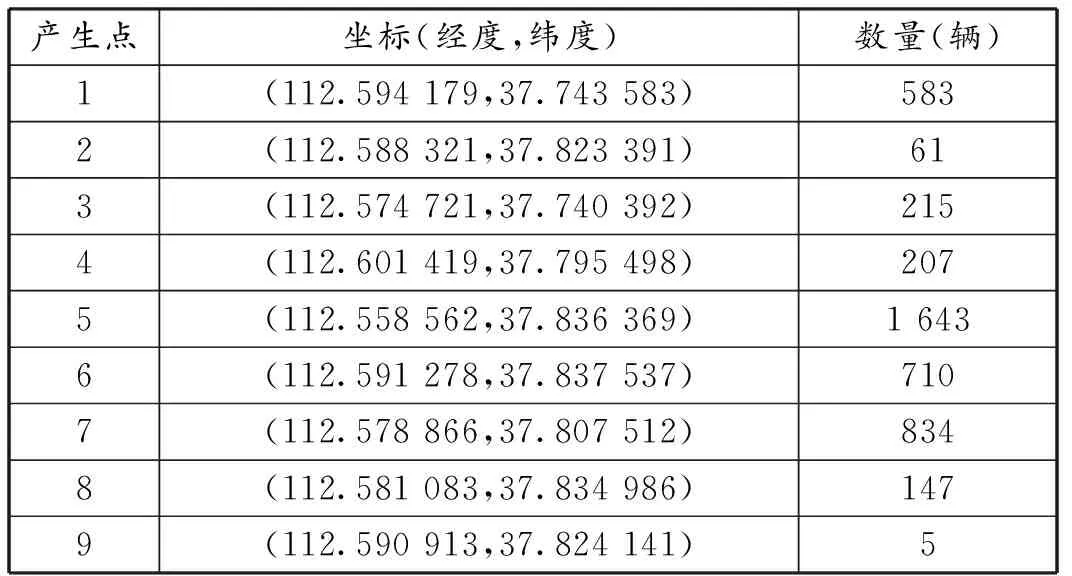
表1 新能源汽车电池产生点位置及对应的新能源汽车电池数量

表2 备选网点坐标

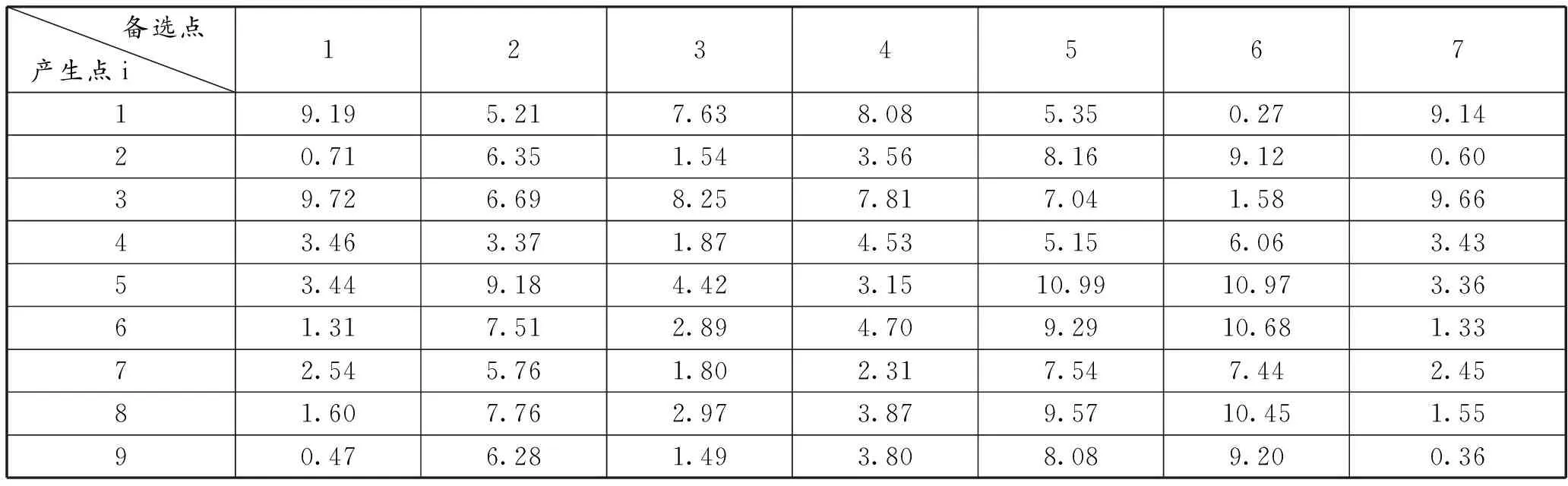
表3 备选网点与新能源电池产生点之间的距离 单位：千米

将算例中的数据带入模型：

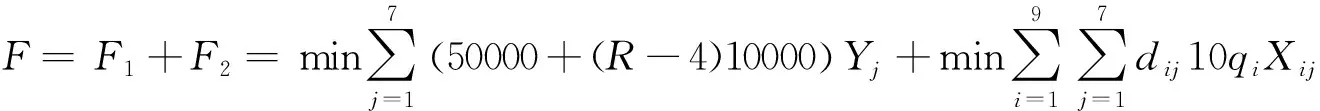
(3-1)

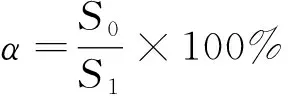
(3-2)

约束条件：0≤dij≤R;i=1,2,…,9.j=1,2,…,7.

(3-3)

∑Xij=1;i=1,2,…,9.

(3-4)

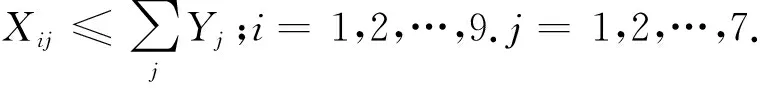
(3-5)

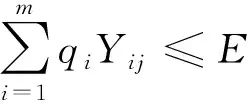
(3-6)

Xij∈{0,1}

(3-7)

Yij∈{0,1}

(3-8)

为了使得计算便捷，利用lingo对模型进行编程，并对网点覆盖的面积进行估算，以判断回收率大小，经过计算后，最后的数据分析结果如表4所示。

通过LINGO对模型进行优化、自动识别，并利用网点的覆盖面积对选出的网点的回收率进行估算，结果进行分析可知，从半径变为13开始，半径每增大1 km，成本增加20 000元，回收率提高3%～4%，以此推算，约在半径为19的时候达到95%的回收率，但是此时网点建立所需要的总费用是较高的；若要求回收率大于85%时，满足要求的时，建立回收网点4、6、7，且半径为9千米，网点对应的容量限制时2 200个，费用为396 364.2元；若回收率大于75%，建立网点4、6、7且半径为8千米或者建立网点6、7半径为19。本模型主要考虑的就是回收率较大，且成本最小，在两个目标的结合下，从求得结果中首选具有86.23%的方案，网点建立选择4、6、7，在同等回收率下比较，不仅成本较小，而且覆盖范围较广，在理想条件下可有效的减少电池的流失，使其高效的回收。该模型相对来说操作简单，能够根据回收区域及市场经济的变动，更便捷的对价格等一些方面的改变做出调整，本文通过实例进行验证，证实了该模型的可行性和便捷性。

表4 Lingo模型求解结果分析

3 结论

新能源汽车电池回收网点建设问题是解决未来大批量电池回收的关键，而且其具备的功能也不仅局限于回收，还包含余能检测、电池置换等其他业务。本文通过建立多目标规划模型对回收网点进行选择，将成本最小和回收率最大作为的主要目标进行求解，选出不同的回收网点，自动识别选取最合适的回收网点个数，并求得对应方案的回收率，便于根据政策的变动和市场的变化做出相应的调整，极大程度上满足了对新能源汽车动力电池回收网点选址的优化，且在解决实际的回收网点选址问题时具有一定的指导和实践意义。