水稻生育期对稻水象甲成虫种群空间格局影响及抽样技术

杨春林， 李洪浩 ， 牟成君， 王 锐， 席亚东

1四川省乐山市植保植检站，四川 乐山 614000； 2四川省农业科学院植物保护研究所，四川 成都 610066； 3四川省乐山市种子管理站，四川 乐山 614000； 4四川省乐山市农技推广站，四川 乐山 614000

稻水象甲LissorhoptrusoryzophilusKusehel是中国进境植物检疫性有害生物和全国农业植物检疫性有害生物(中华人民共和国农业部，2009)，该虫适生范围广、扩散能力强、扩散速度快(丁新华等，2017)，成虫取食上表皮及叶肉组织，在叶片上形成灰白色条斑，幼虫则钻蛀根内取食，或直接咬断稻根，造成水稻植株长势变缓、生育期延长(王小武等，2018)，甚至造成水稻坐兜或形成浮秧(何永福等，2013)，一般可导致水稻减产20%～30%，严重时可达50%以上，甚至绝收(蔡明等，2000)。稻水象甲起源于北美洲中南部密西西比河流域，1976年进入日本后扩散到朝鲜半岛(邱良妙等，2007)。自1988年首次在河北省唐山市发现以来，稻水象甲在我国沿渤海湾迅速扩散蔓延，目前已涉及23个省(区、市)463个县(市、区)(丁新华等，2019)，在部分地区已成为水稻的主要害虫之一。四川省2011年首次在内江地区发现稻水象甲入侵(何春兰和何军，2013)，随后该虫迅速在全省扩散，截至2018年底，四川省共有16个市州54个县(市、区)发生，发生面积近66.7万hm2(四川省农业农村厅，2018)。稻水象甲蔓延速度快、危害损失重、对环境的适应能力强，防治难度很大，若得不到有效控制将严重威胁本地区水稻生产。

生物种群空间是指生物种群的栖居场所，即生境，种群空间格局则是该生物种群在其生境空间的分布结构，是显示物种种性的生态学性质之一(沈佐锐和管致和，1986)，常常影响种群的内部结构和个体行为(蔡小明，1991)。科学开展抽样调查，准确获取农业昆虫的种群密度是实施有害生物综合治理方案的先决条件，而抽样方法的理论基础之一是种群的空间格局。因此，研究稻水象甲种群的空间格局对制定科学的调查取样方案、综合防治策略具有重要意义(于新文和刘晓云，2001)。目前，国内已有贵州(峗薇等，2013)、新疆(王小武等，2017)、广西(张燕杏等，2016)等省份(自治区)报道了稻水象甲种群空间分布规律及抽样技术的研究，四川省未见相关报道。由于农业昆虫种群的空间格局受地理环境、耕作习惯和栽培方式、寄主植物种类及发育阶段等外部因素影响(峗薇等，2013)，现有研究结果的应用具有一定局限性。稻水象甲防治经验表明，稻水象甲成虫的有效防控是控制疫情蔓延和减轻危害的关键(周社文等，2006)。本试验于2019年对四川西南浅丘稻区稻水象甲成虫种群空间格局进行了研究，探讨了水稻2个重要时期，即分蘖期和抽穗期对稻水象甲成虫种群空间聚集特性的影响，提出了操作简便、快捷的大田抽样技术，并运用模拟抽样的方法比较不同抽样方法的适合性与代表性，以期为获取准确的虫情调查资料，制定综合防控措施提供理论依据。

1 材料与方法

1.1 试验区概况

试验田位于四川省乐山市井研县天云乡瓦子坳村(E103°55′3″，N29°51′29″)。井研县位于四川盆地西南，县城北距成都市142 km，西至乐山市37 km，东南至自贡市118 km，与仁寿、青神、荣县、犍为、五通桥、市中区等地接壤。井研县地势低矮，海拔高程在380～450 m；丘陵广布，溪沟纵横。井研属四川盆地中亚热带湿润气候区，气候温暖湿润，年平均气温17.2 ℃，年平均日照总数1134.6 h，年平均降雨量1025.8 mm。

1.2 试验设计与调查方法

在常年发生稻水象甲疫情的区域选取12块相邻的稻田，随机分成2组，每组6块田，第1组3月22日播种水稻，5月1日移栽；第2组5月10日播种，6月10日移栽，均采用水育秧方式。2019年6月25日稻水象甲1代成虫羽化盛期，调查所有田块稻水象甲成虫，采用平行取样法，将每块田均分为100等份，即10行10列，于行列交汇处取1丛水稻，共100丛，调查水稻叶片上及根基处所有稻水象甲成虫并计数。试验区水稻主栽品种为宜香优2115、晶两优1377，水稻丛距20 cm，行距30 cm，种植密度0.7～0.8万株·hm-2。

1.3 空间分布型测定

1.3.1 聚集度指标法 统计调查数据，计算不同田块稻水象甲成虫平均密度值m(头·丛-1)和方差S2，依据6个指标进行判断：(1)Beall扩散系数：C=S2/m；(2)David和Moore的丛生指标：I=S2/-1；(3)平均拥挤度：m*=m+S2/m-1；(4)Lloyd聚块性指数：m*/m=(m+S2/m-1)/m；(5)Cassie的聚集度指数：CA=(S2-m)/m2；(6)Waters负二项分布K值：K=m2/(S2-m)。各个聚集度指标的计算及判断标准参考阎雄飞等(2019)。

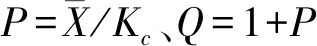
1.3.3 回归模型法 Taylor幂法则(Tayloretal.，1961)：Taylor提出的样本平均数(m)与方差(S2)对数值之间的回归关系公式lgS2=a+blgm。其中a是一个与样本大小和计算方法有关的因子，受环境异质性的影响；b为聚集特征指数，其指示聚集度与种群密度依赖性的关系。当a=0，b=1，说明种群为随机分布；当a>0，b=1，说明种群为聚集分布；当a<0，b<1时，种群密度越高分布的越均匀；当a>0，b>1，说明种群在一切密度下均是聚集分布，且聚集性具有密度依赖性，即m越大种群聚集度越高。

Iwao的m*-m回归分析法(Iwaoetal.，1968)：m*-m的回归方程为m*=α+βm，其中常数α和β揭示种群的分布特征，α为分布的基本成分按大小分布的平均拥挤度，β为基本成分的空间分布图示。当α=0时，分布的基本成分为单个个体；α>0，分布的基本成分是个体间相互吸引的个体群；α<0，个体间相互排斥。当β<1时，为均匀分布；β=1，为随机分布；β>1，为聚集分布。

1.4 聚集原因分析

根据Blackith (1958)提出的种群聚集均数(λ)法分析稻水象甲成虫的聚集原因，聚集均数公式为λ=mγ/2k，γ为自由度等于2k的2(卡方)分布函数，即γ等于“2值表”中自由度等于2k与概率(p=0.05)对应的值，由于2k常为小数，因此值可用比例内插法求得。当λ<2 时，昆虫聚集原因只可能是某些环境因素所致；当λ≥2时，昆虫聚集原因是昆虫本身的聚集习性或与环境因素综合作用所致。

1.5 抽样技术

1.6 抽样方法比较

选取一形状方正的稻田，对稻水象甲成虫进行全田普查(逐行逐丛进行调查)，将调查数据填入Excel表格，制成田间实际分布图。分别用五点抽样法、棋盘式抽样法、双对角线抽样法、Z形抽样法、平行线抽样法在空白Excel表上进行模拟抽样，每种方法调查30丛水稻，以田间实际分布情况作为参照进行单样本T检验，确定最佳抽样方法。

1.7 数据处理

运用SPSS Statistics 25软件进行方差分析、频率统计和单样本T检验，采用Duncan氏新复极差法检测差异显著性；用Excel 2003进行简单运算并绘图。

2 结果与分析

2.1 空间格局判定

2.1.1 聚集度指标测定 在第1代稻水象甲成虫羽化盛期调查时，第1组水稻正处于抽穗期，第2组水稻处于分蘖期。调查结果显示，所有调查田块(12个田块)稻水象甲成虫平均密度为0.48～5.83头·丛-1，分蘖期水稻田虫口平均密度显著高于抽穗期。由表1可看出，所有田块的平均拥挤度m*均大于m，聚块性指数m*/m、扩散系数C均大于1；David和Moore的I指标、Cassie指标CA均大于0；负二项分布K值大于0小于8。上述各指标表明所调查田块稻水象甲成虫种群均呈聚集分布。且处于水稻分蘖期田块的平均拥挤度m*、扩散系数C、David和Moore的I指标和负二项分布K值明显大于水稻抽穗期田块，而聚块性指数m*/m和Cassie指标CA值则相反，表明同一时间，处于不同生育阶段稻田中稻水象甲成虫的田间聚集行为具有差异性。

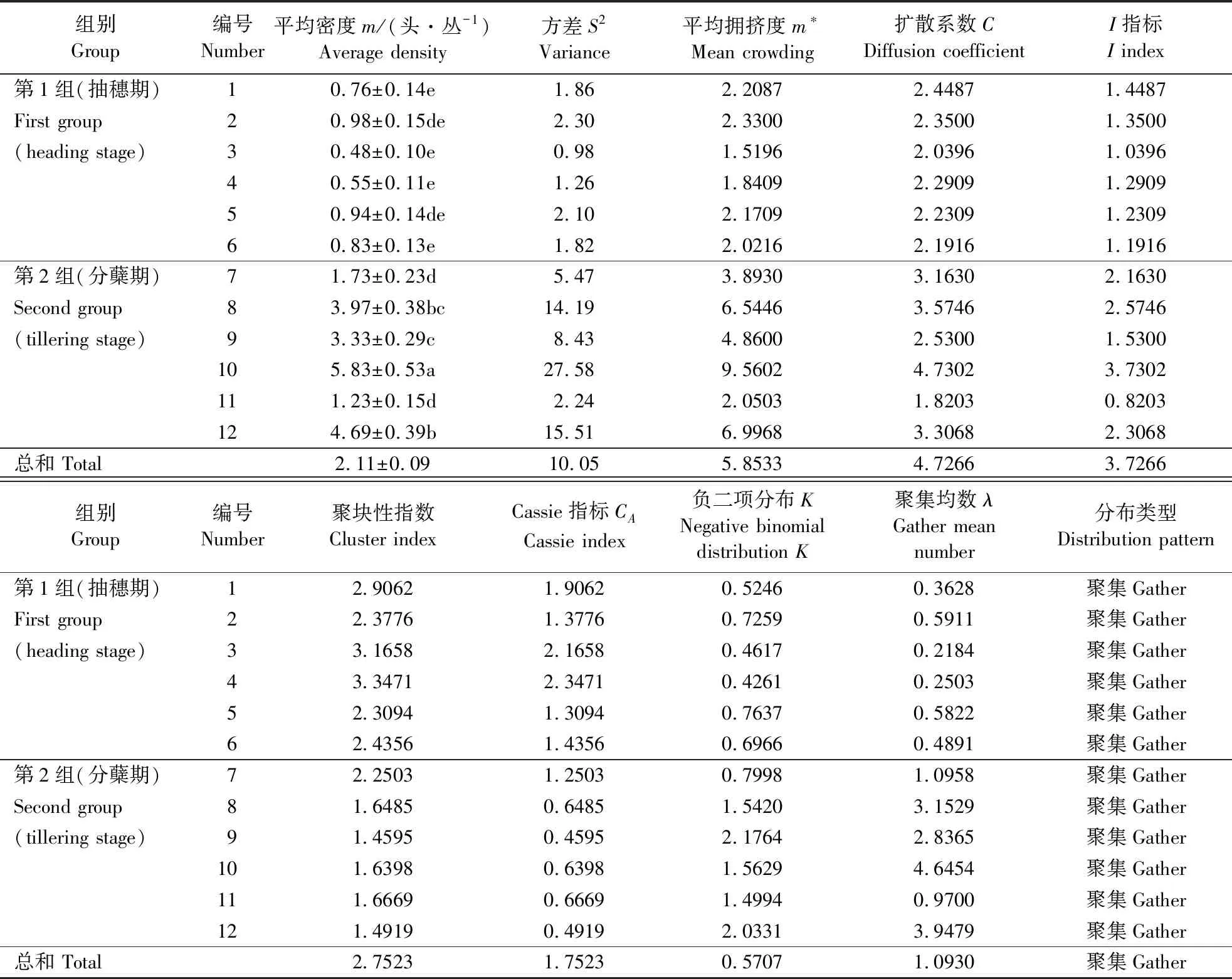
表1 稻水象甲成虫的聚集度指标Table 1 Aggregation index of L. oryzophilus adult

2.1.2 Taylor幂法则 根据表2数据，将方差S2和平均密度m作对数转换，得水稻分蘖实验组稻水象甲成虫的S2-m回归方程为lgS2=0.2766+1.4336lgm(R=0.9535**)，抽穗实验组为lgS2=0.3681+1.11lgm(R=0.9728**)。方程的截距a均大于0，斜率值b均大于1，说明在2种水稻生育期条件下，稻水象甲成虫种群均呈具密度依赖性的聚集分布，即m越大种群聚集度越高。分蘖期稻田的斜率(b=1.4669)大于抽穗期稻田(b=1.3121)，说明种群密度越高，聚集度对密度m的变化越敏感。将2组稻田作为一个样本总体进行回归分析，得回归方程：lgS2=0.3747+1.2571m(R= 0.9795**)，说明水稻生育期的差异可能会影响成虫的种群密度，但不会影响其空间格局。

2.1.3 Iwao的m*-m回归分析 分蘖期稻田稻水象甲成虫的m*-m线性回归方程为m*=0.5706+1.4669m(R=0.9568**)；抽穗期稻田为m*=1.0224+1.3121m(R=0.8203*)；样本总体回归方程为m*=0.8925+1.3936m(R=0.9770**)。其中截距α均大于0，可认为水稻不同生育期条件下稻水象甲成虫在田间分布的基本成分为个体群，个体间相互吸引；斜率值β均大于1，表明稻水象甲成虫总体呈聚集分布。因为分蘖期稻田虫口密度较高，加之分蘖期稻田的斜率(β=1.4669)大于抽穗期稻田(β=1.3121)，说明由于个体间的相互吸引效应，分蘖期稻田的稻水象甲成虫种群聚集度高于抽穗期稻田，结果与Taylor幂法则判定相一致。

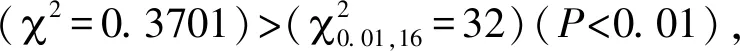
表2 稻水象甲成虫的负二项分布拟合优度检验Table 2 Goodness of fit test of negative binomial distribution of L. oryzophilus adults

2.2 聚集原因分析

按照Blackith提出的种群聚集均数(λ)法，根据表2中的负二项分布K值和样本平均密度m，采用比例内插法算出自由度2k时的估计值，最后求得聚集均数λ值。将表中的平均密度m与聚集均数λ作线性回归分析，得λ=-0.2199+0.8603m(R=0.9952**)，表明聚集均数与种群密度呈显著正相关(图1)。将λ=2代入方程式，得m=2.58，即当稻水象甲成虫种群密度m<2.58时，其聚集是由环境作用所引起；当稻水象甲成虫种群密度m≥2.58时，其聚集为其自身的聚集习性或与环境因素综合作用所致。

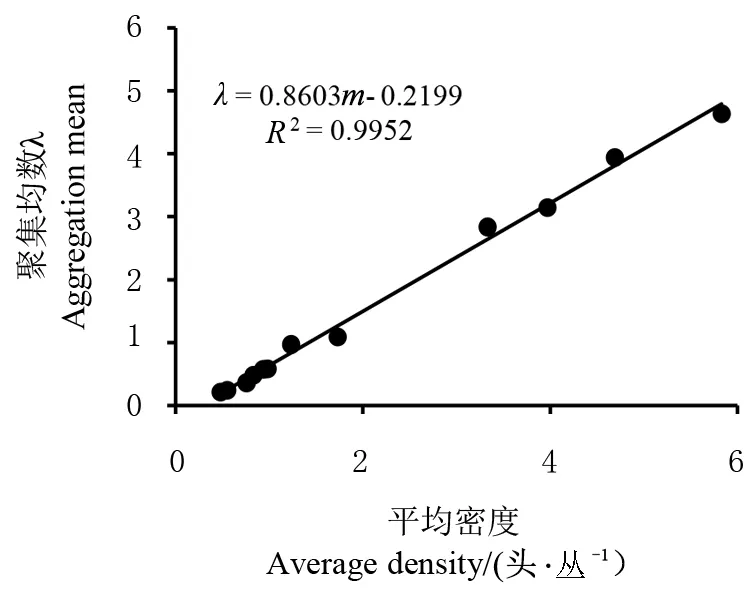
图1 聚集均数与平均密度的线性回归关系Fig.1 Linear regression relationship between aggregate mean and average density

2.3 抽样技术

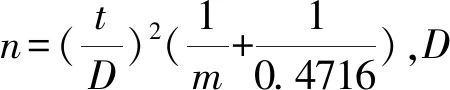
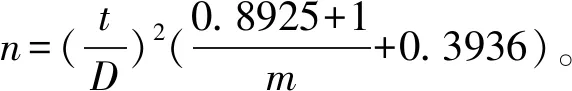
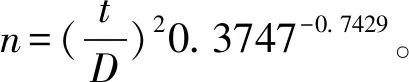
通过Southwood的Kc法、Iwao回归法及Taylor幂法理论抽样模型分别求得稻水象甲成虫在不同种群密度和精度要求下的理论抽样数n(表3)。结果表明，不同理论抽样模型得出的理论抽样数差异明显，其中Iwao回归法的理论抽样数最高，Taylor幂法的理论抽样数最低，且3种方法的理论抽样数均随种群密度(m)和估计精度(D)值的增高而逐渐减小。在实际应用中，D值可根据实际情况进行调整，当种群密度较低时抽样数较大，可将D值取大些(如0.3)，当种群密度较高时，应将D值取小些(如0.1)以提高抽样精度。

表3 稻水象甲成虫种群理论抽样表Table 3 Theoretical samplingTable of adult population of L. oryzophilus

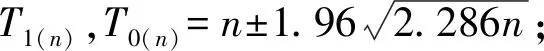
表4 稻水象甲成虫种群理论抽样表Table 4 Sequential sampling sequence of L. oryzophilus adults

图2 稻水象甲成虫复序贯抽样图Fig.2 Complex sequential of L. oryzophilus adults

2.3.3 抽样方法比较 分别对5种常用抽样方法进行模拟抽样比较，并分别将其与田间实际密度作单样本T检验(检验值0.62)，具体检验参数见表5。各种抽样方法与检验值的均值差从小到大依次为双对角线法(-0.0867)、平行线法(0.1476)、五点法(0.1800)、Z形法(0.2800)、棋盘式法(0.6467)，说明双对角线法抽样结果与实际值之间差异最小，棋盘式法抽样差异最大。所有调查方法的sig值(双侧)均大于0.05，表明几种抽样方法的结果与田间实际分布差异均不显著，均适用于稻水象甲成虫的田间抽样；其中，双对角线线抽样法的适合性最好，平行线抽样法次之，棋盘式抽样法最差。综上可知，双对角线抽样法是稻水象甲成虫田间抽样的最佳方法。由于水稻植株较密，人工抽样调查时会触碰植株和叶片造成稻水象甲成虫掉落或迁飞，从而影响调查结果，试验采用模拟抽样的方法，避免在同一块田反复调查造成人为误差。

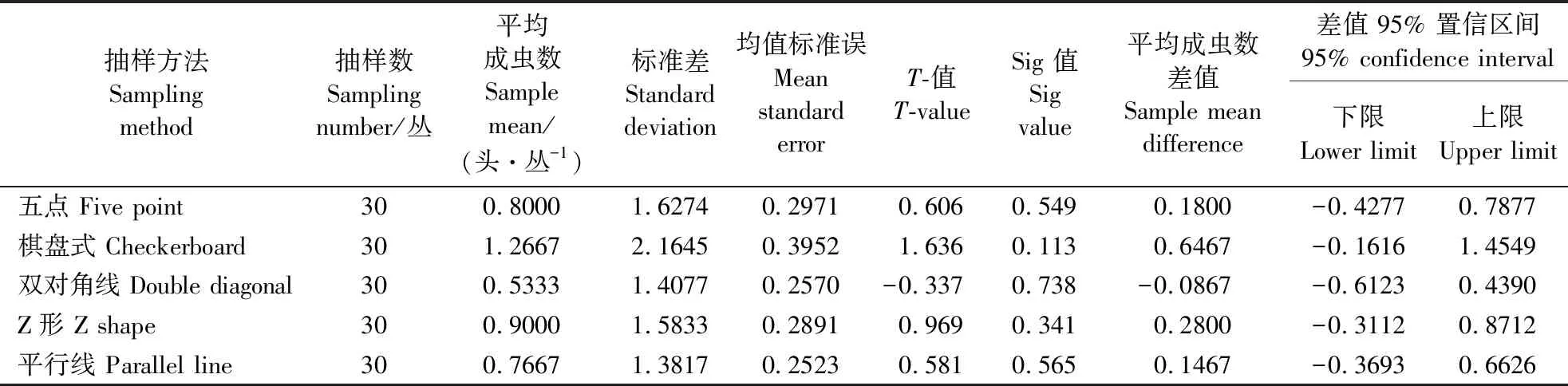
表5 稻水象甲成虫田间抽样方法比较Table 5 Comparison of field sampling methods for L. oryzophilus adults

3 讨论

研究生物种群空间格局常用的方法主要有聚集度指标判定法、回归模型分析法(Iwao回归法、Taylor幂法)、概率分布模型法(频数分布拟合2检验法)等(王文琪等，2010)。目前，针对稻水象甲种群空间分布的研究主要集中在前2种方法，未见采用概率分布模型法的相关报道。本研究采用聚集度指标法和回归模型法分析水稻生育期对稻水象甲成虫的空间聚集特性的影响，并运用频次卡方检验法进行稻水象甲成虫种群负二项分布拟合优度检验，结果表明，稻水象甲成虫在不同水稻生育期稻田间呈负二项聚集分布，基本成分为个体群，个体间相互吸引，聚集强度随种群密度的升高而增加，且种群密度越高，聚集强度对种群密度的变化越敏感。与曲辉等(1998)在辽宁的研究相同，与峗薇等(2013)报道的贵州高原山地稻水象甲幼虫空间分布型基本一致，均为聚集分布。通过种群聚集均数法分析稻水象甲成虫聚集原因，结果表明，当稻水象甲成虫种群密度较低(m<2.58)时，其聚集由环境作用引起；当稻水象甲成虫种群密度较高时(m≥2.58)，其聚集为其自身的聚集习性或与环境因素综合作用所致。

昆虫生态学研究中常见的分布型主要是二项分布(均匀分布)、Poisson分布(随机分布)、负二项分布(聚集分布)，且在一定条件下不同分布型之间可能会相互转化(周国法和徐汝梅，1998)。研究昆虫分布规律时，要准确判断其空间格局是否符合负二项分布，可利用估算的聚集性分布参数公共K值拟合理论频数，并结合实际频数作卡方检验进行验证。实际应用中估算K值方法较多，不同估计方法有时会对拟合效果造成是或否这种极端判断上的直接影响(张连翔等，1996)。在一些报道中，部分学者仅凭单一方法估算的K值大小即判定是否符合负二项分布(峗薇等，2013)，其结论缺乏支撑，准确性值得商榷。本文采用常用的4种方法估算K值，结果表明，采用矩法证实稻水象甲成虫不是负二项分布(P<0.01)，频数法、零频率法和最大似然法则证实稻水象甲成虫符合负二项分布(P>0.05)。在几种估算K值的方法中，矩法计算相对简单，但效率不高，最大似然法虽计算略繁琐，但结果最精确(王海银等，2009)，因此在实际操作中当其他几种方法均不能作出准确判断时，则应采用最大似然法进行最后验证。

本试验通过调整水稻播栽时间的方法错开2组试验田水稻生育期，因推迟移栽的稻田在稻水象甲产卵和幼虫发育阶段无水生植物作为寄主，其虫源为第1代成虫羽化后迁入。将不同生育期稻田中的稻水象甲成虫种群分布型构成的连续的动态系统作为研究对象，最大限度地消除了越冬成虫迁移、产卵习惯和幼虫聚集行为的影响，利于研究第1代成虫自身的种群空间分布规律。由于稻水象甲成虫取食具有一定的趋嫩性，分蘖期的水稻生长代谢旺盛，抽穗期的水稻叶片硬化程度较高，导致分蘖期稻田中稻水象甲成虫平均密度显著高于抽穗期。研究发现，昆虫具有“分布的不确定性”，即1组资料可能同时符合几种分布模型，也可能不符合任何分布模型(张连翔等，1996)。本研究发现，当调查的所有田块稻水象甲成虫作为一个总体，即将12块稻田的所有调查数据作为一组资料时，符合负二项分布模型，当分别将抽穗期和分蘖期田块作为总体时，则均不符合负二项分布，其原因可能是在对应种群密度条件下样本量太小或分布的自由度达不到2检验方法的要求。这一现象说明，虽然稻水象甲成虫种群的聚集度具有密度依赖性，但是种群密度或水稻生育期的差异不影响其负二项分布概率模型的拟合和描述。

昆虫从种群的建立到繁殖壮大，是一个种群密度不断增高的动态过程，新入侵昆虫种群的空间格局可能随繁殖和时间推移而变化，种群所有可能的分布类型在这个动态过程中组成了一端均匀分布，另一端高度聚集的连续系统(沈佐锐，1992)。稻水象甲自2011年入侵四川稻区，已经进行了近10年的繁殖、适应和进化，可认为该地区稻水象甲种群空间格局已经成型并达到稳定阶段。因此，根据本研究得出的稻水象甲成虫空间分布相关模型参数确立的稻水象甲成虫的抽样技术，对当前稻水象甲的防治和疫情监测具有指导意义。由于稻水象甲是迁飞性害虫，越冬代成虫在迁入稻田初期的分布规律易受边际效应影响，本研究结果在实际应用中有一定的局限性。另外，本次调查样本所在区域为典型的四川西南地区浅丘地貌，成都平原和川西高原地区的特殊地理环境和当地农事操作习惯对稻水象甲种群空间格局的影响有待进一步研究。