底泥磷释放对藻类种群动力学的影响

郝丽娜， 虎佳尧， 李永坤

(长春工业大学 数学与统计学院， 吉林 长春 130012)

0 引 言

水生生态系统在人类的生活环境中起着十分重要的作用。伴随着人口不断增加、城镇化进程不断加速,以及工农业不断发展，整个水生态系统受到非常严重的影响，如水生态系统的自净能力变弱、流动水域更新和交替的周期变长等，都使得水生态系统的富营养化变得更严重[1]。丹麦生态学家Jorgensen[2]认为水体中的浮游动物和藻类的生长是水体富营养化的主要原因。因为在短时间内，藻类生物的疯狂繁殖导致了水华现象此起彼伏。因此对人类的生存、健康和整个社会环境造成了很大影响。

在整个水生态系统中，底泥在其中扮演着“源”和“汇”的角色，它能够不断接收水体中的沉积物，同时朝水体释放营养，在水生态系统中具有举足轻重的地位，发挥着无可替代的作用[3-8]。浅水湖的底泥营养盐释放是个非常复杂且重要的过程。但是大多数研究集中在生物学或者生态学上，以野外实验或者实验室数据分析为主，探讨因素之间的作用关系[9-14]。

另外，一些相关研究建立带有底泥系统的营养盐循环的数学模型，但是往往以数值计算和模拟为主[16-18]，对底泥系统的机理性分析并不多见，且不深入，关于底泥系统的种群动力学模型更是鲜见。

生态种群动力学是一个以数学理论和方法研究生态学的重要分支，具有广阔的应用范围和发展空间，生态种群动力学已广泛应用于水生态系统问题研究中[19-21]。因此,文中应用生态种群动力学模型系统地研究底泥对藻类爆发的影响，从而为底泥疏浚和控制藻类爆发提供一定的理论依据。主要研究内容包括以下几方面：

1)基于种群动力学建立关于营养元素(磷)-藻类-浮游动物的生态数学模型；

2)利用定性分析理论分析模型的动力学行为；

3)对模型进行数值分析；

4)讨论底泥疏浚对藻类爆发的影响机制。

1 模型建立

考虑一个由藻类、浮游动物、可溶性磷、底泥和外部流入磷构成的水生态磷循环系统，可溶性磷被藻类作为营养成分吸收，而藻类的死亡和新陈代谢又会分解磷返回到水体中，同时水生态系统底泥中磷不断释放到水中，构成一个循环系统，如图1所示。

图中，A(t)、P(t)和Z(t)分别为时间t时藻类的密度、水中可溶性磷的密度和浮游动物密度，单位分别为mgC/L,mgP/L,mgC/L，简记为A、P、Z。

由图1可知，被藻类利用吸收的可溶性磷来源有四种方式：外部流入的磷、底泥中磷的释放、浮游动物和藻类死亡或新陈代谢后被分解产生的磷。输出则主要归因于藻类吸收的磷和水体的稀释作用。藻类依靠吸收营养物质(磷、氮等)生长，通过被其它动物捕食、自然死亡和内部竞争从水中消除。

根据藻类的营养吸收速率与温度g(T)和光照h(Iin,A)有关[19]，为了简化，文中假设水生态系统的环境温度和日常光照强度都是保持恒定不变的，即

g(t)=h=1，

可以建立数学模型

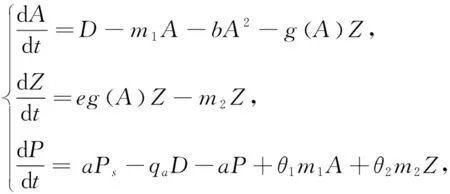
(1)

式中：D=f(P)A;

bA2----藻类种群内部竞争损失;

aPs----释放到水中的可溶性磷，其中包含外部流入和底泥中释放的磷;

a----水体对可溶性磷的稀释比例;

qa----藻类的磷碳比，即藻类体内磷与体内碳比例，其影响藻类对磷的吸收;

aP----水体对可溶性磷的稀释造成的损失。因此，aPs-aP代表水体内部与外部的营养交换;

θ1m1A----藻类经过新陈代谢和死亡后按照比例θ1分解释放的可溶性磷;

θ2m2Z----浮游动物经过新陈代谢和死亡后按照比例θ2分解释放的可溶性磷。

假定藻类的损失率与密度A成正比，系数为m1；藻类的增长受可溶性磷影响，其增长率为

式中：m----半饱和参数。

浮游动物通过捕食藻类生长，假设捕食功能性反应函数为HollingI型，即

g(A)=cA，

式中：c----捕食率。

水体中可溶性磷的流入部分可表示为

Ps=Pin1+γ1(βPin2+Pb)+γ2(1-β)Pin2，

(2)

式中：Pin1----可溶性磷浓度;

Pin2----颗粒态磷浓度;

Pb----底泥中磷的浓度。

水体中的可溶性磷浓度跟Pin1、Pin2和Pb都有密不可分的关系。假设外部的磷以恒定速率Pin=Pin1+Pin2流入，底泥中的磷Pb和颗粒态磷Pin2分别以γ1和γ2的速度释放可溶性磷到水中，颗粒态磷Pin2按比例β沉淀到底泥中。

由于底泥中磷的释放作用，式(2)可简化为

Ps=P0+γ1Pb。

(3)

文中忽略藻类和浮游动物由于死亡而释放到底泥中颗粒磷。

2 定性分析

对模型(1)进行分析，设:

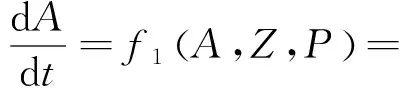
G1A-m1A-bA2-cAZ，

aP0+aγ1Pb-G2A-aP+G3，

G3=θ1m1A+θ2m2Z。

经计算可得模型(1)的Jacobian矩阵为

式中：F1=G1-m1-2bA-cZ;

F3=θ1m1-G2;

系统(1)可能存在三类平衡点，边界平衡点

E1=(0,0,P1),

E2=(A2,0,P2),

E3=(A3,Z3,P3)。

为求得平衡点，需解下面方程组

(4)

首先求

E1=(0,0,P1)，

由

aP0+aγ1Pb-aP1=0 ，

解得

P1=P0+γ1Pb。

因此求出边界平衡点

E1=(0,0,P0+γ1Pb)。

系统(1)在点E1的Jacobian矩阵为

下面求J(E1)的特征值,即

|λE-J(E1)|=0，

可得

解得

λ2=-m2<0,

λ3=-a<0。

因此当

时，

E1=(0,0,P0+γ1Pb),

是局部渐近稳定的。

综上分析可得定理1。

定理1系统(1)的边界平衡点E1=(0,0,P1)总是存在，且当

成立时，它是局部渐近稳定的。

下面分析平衡点E2=(A2,0,P2)的存在性和稳定性。因为A=A2,Z=0,P=P2满足方程组(4)，所以满足

(5)

aP0+aγ1Pb-G4A2-aP2+θ1m1A2=0,

(6)

由式(5)解得

由式(6)解得

φ(P2)和ψ(P2)的函数图像如图2所示。

由图2可知，在φ(P2)中A2关于P2是单调递增的，而在ψ(P2)中A2关于P2是单调递减的。当P2=Ps=P0+γ1Pb时，ψ(P2)=0。

因此由介值定理可得，若φ(Ps)>0，则存在唯一一点P2，使得φ(P2)=ψ(P2)，对应函数值记为A2，于是可得系统(1)的边界平衡点为E2(A2,0,P2)。

系统(1)在E2的Jacobian矩阵为

其特征方程为

|λI-J(E2)|=(ecA-m2-λ)(K1-K2),

式中：K1=(-bA2-λ)(-H3-a-λ);

K2=H2(θ1m1-G4)。

综上分析可得定理2。

定理2当φ(Ps)>0时，系统(1)存在边界平衡点E2(A2,0,P2)，且当

ecA-m2<0,

和

bA2(H3+a)-H2(θ1m1-G4)>0,

成立时，则平衡点E2(A2,0,P2)是局部渐近稳定的。

对于系统(1)的正平衡点E3=(A3,Z3,P3)，A=A3,Z=Z3,P=P3是方程组 (4)的解，因此有

O1=θ1m1A3;

O2=θ2m2Z3。

化简得

(7)

(8)

aP0+aγ1Pb-G5A3-aP3+O1+O2=0,

(9)

由式(7)得

式中：Q=m1+bA3+cZ3。

把上式代入式(9)可整理得

再由式(7)整理可得

μP3=mQ+P3Q,

即

(μ-Q)P3=mQ,

解得

定义两个函数

显然R(Z3)关于Z3递减，T(Z3)关于Z3递增，若两曲线在第一象限有交点，且坐标点为(Z3,P3)，则得E3=(A3,Z3,P3)。进一步利用Jacobian矩阵

判断E3是否为局部渐近稳定的。由于系统(1)的复杂性，文中没有给出关于局部稳定性的判据。

3 数值分析

对系统(1)进行了定性分析，研究系统平衡点类型及其存在条件，使用Jacobian矩阵讨论了边界平衡点的局部渐近稳定性。然而，由于该系统具有非线性和复杂性，因此未实现系统全局稳定性的结果。为更加直观地说明系统的动力学行为，利用数值模拟分析水生态系统中的藻类动力学行为。

系统参数取值见表1。

首先研究系统(1)中底泥中磷的不同浓度(Pb)对系统动力学行为的影响，如图3所示。

由图3可以看出，当Pb较低时(Pb=0.5)，系统只存在少量可溶性磷，藻类和浮游动物灭绝(见图3(a))；

当Pb增加时(Pb=0.65)，藻类可以生存，浮游动物灭绝(见图3(b))；

当Pb较大时(Pb=0.9或Pb=1.2)，藻类和浮游动物稳定共存(见图3(c)和(d))；

当Pb继续增加(Pb=1.4)，藻类和浮游动物稳定共存，达到稳定状态时的种群密度也会随着Pb的增加而增加(见图3(e))。

水生态系统中种群存在的种类和数量会随着底泥磷释放的浓度变化而变化。当底泥磷释放浓度较低时，由于水体中可溶性磷浓度太低，不足以支撑藻类生长所需养分，因此藻类不会在磷浓度过低的水体中生长，所以它的浮游动物也不会出现。随着底泥磷释放浓度逐渐增高，藻类开始慢慢繁殖，但此时浮游动物由于藻类的质量不好和数量不足难以生存，同时由于藻类的死亡和其种群内部竞争作用造成的藻类数量以一定的比例损失，藻类就会和底泥磷释放浓度在密度上达到一定平衡。当底泥磷释放浓度继续升高时，藻类就会大量繁殖，当藻类的质量和数量能够满足它的浮游动物生存时，底泥磷的浓度、藻类和浮游动物的密度就会达到一定的平衡。

水体稀释速率变化对系统(1)的影响如图4所示。

我们考虑当底泥磷释放浓度(Pb)恒定，水体对可溶性磷的稀释速率a对系统动力学行为的影响(见图4)。当a较大时，系统中可溶性磷可以维持藻类和它的浮游动物共存(见图4(a))；当a减小时，系统中可溶性磷只能维持小部分藻类稳定生存，它的浮游动物逐渐走向灭绝(见图4(b)和图4(c))；当a很小时，由于水体对可溶性磷的稀释作用过强，系统中可溶性磷含量过少，藻类和浮游动物均灭绝(见图4(d))。由此可见，水体对可溶性磷的稀释速率越大，藻类赖以生存的养分不充足，藻类数量就会越少。

表1 模型1中参数的定义、单位和取值

4 结 语

应用种群动力学来研究水生态系统中底泥磷释放对藻类种群动力学的影响。首先根据种群动力学建立了关于营养元素-藻类-浮游动物数学模型。利用定性分析理论讨论了该系统中可能存在的平衡点类型,以及边界平衡点的局部渐近稳定性。

利用数值分析讨论了系统中底泥磷释放和水体稀释比例对藻类种群动力学行为的影响。随着底泥磷释放浓度的不断升高，系统经过了以下演变：藻类-浮游动物种群均灭绝、只有藻类种群存在、藻类种群和浮游动物种群稳定共存。只有总磷浓度适中的时候,两种群达到稳定共存。

在防治和治理水体中藻类爆发灾害时,可以考虑对水体底泥进行疏浚，通过降低底泥磷释放浓度,或者增加水体中稀释速率来抑制藻类生长。

文中只考虑底泥磷释放浓度对系统的影响。实际上底泥磷的释放是个复杂的过程，影响因素很多，既有生物因素，也有非生物因素，可以将每个因素在模型中刻画描述，并加以研究。另外，文中假设底泥中磷含量为常值，实际上底泥中磷含量是时变的，因此也可以考虑底泥中磷含量是状态变量的系统来研究。

随着科学技术的进步，随之而来产生越来越多实际且复杂的问题。种群动力学结合各学科领域，为解决问题提供新方法和新视角，将问题简化，进行定性研究。生物数学一定会有更大的进步和广阔的发展。