基于粒子群优化算法的T/R组件相位非线性分析

刘建勇 陈兴国

(中国电子科技集团公司第三十八研究所 合肥 230088)

0 引言

T/R组件是相控阵雷达中装机量最大的核心部件，其性能直接影响着雷达整机的技战指标。相位非线性是考察T/R组件发射和接收链路传输相位非线性失真的一个参数，该指标的好坏对相控阵雷达尤其是采用脉冲压缩体制的相控阵雷达来说至关重要，决定了脉冲压缩的效果和雷达探测的距离分辨率[1]。

在T/R组件测试技术中，通常采用曲线拟合方法[1-2]进行计算，即根据测试的相位值经过去翻转处理后拟合出一条直线，根据目标拟合曲线与测试相位值之间偏差的峰峰值求得。文献[2]给出的拟合方法为最小二乘法(Least Square Method,LSM)，我们利用该方法计算得到的T/R组件相位非线性误差与通过矢量网络分析仪测试得到的结果总有或大或小的偏差。

本文给出了一种基于粒子群优化算法的相位非线性误差新求解办法，并通过与实际测试结果对比验证了算法的准确性，同时通过大量测试数据对比了最小二乘法与本文的区别，表明最小二乘法求解结果普遍比实际偏大，影响了T/R组件指标测试的准确性。

1 相位非线性及粒子群优化算法简介

1.1 T/R组件相位非线性

对于一个线性传输系统，其传输相位应是频率f的线性函数，如公式(1)所示。

φ(f)=α+βf

(1)

但实际上，T/R组件由于收发链路中的放大器尤其是处于饱和区工作的末级放大器带来的非线性失真、多级放大器之间的失配及耦合串扰、金属封装带来的腔体效应等因素都会对相位曲线带来非线性畸变。

对于T/R组件，通过矢量网络分析仪调节电延时来去除其线性部分，剩下的偏离线性相位的峰峰值，即为非线性误差。但是通过此种测试方法效率低下不能适应T/R组件大批量全自动测试的要求。

通常采用对测量相位按公式(1)进行直线拟合来快速计算相位非线性误差。对于一组测试数据(fi,pi)，fi为测试频率，pi为对应的相位值，i=1,2,…,NP，NP为测量频率点数。定义残差δi为相位拟合值与测量值的偏差，即如公式(2)所示。

δi=φ(fi)-pi=α+βfi-pi

(2)

最小二乘法的拟合目标是残差平方和最小[3]，即找到一组最优的(α,β)，满足公式(3)

(3)

经过验证，利用最小二乘法计算得到的T/R组件相位非线性误差与通过矢量网络分析仪测试得到的结果总有或大或小的偏差。因此需对拟合目标进行改进。本文采用的拟合目标为残差峰峰值最小法，如公式(4)所示。

(4)

对于公式(4)的求解我们采用粒子群优化算法，详述如下节。

1.2 粒子群优化算法

粒子群优化算法(Particle Swarm Optimization, PSO)是一种进化计算技术(Evolutionary Computation)，最早是由Eberhart和Kennedy于1995年提出[4]，它的基本概念源于对鸟群觅食行为的研究。该算法从随机解出发，通过迭代寻找最优解，是一种基于多个个体协同合作和信息共享的仿生技术。

假设在D维空间中，有N个粒子。PSO算法用位置和速度两个向量来描述粒子的属性，第i个粒子位置向量定义为：Xi=(xi,1,xi,2…,xi,D)，速度定义为Vi=(vi,1,vi,2,…,vi,D)。通过目标函数可以确定适应值，从而知道自己到目前为止发现的历史最好位置，这个解称之为个体极值，记作(pi,1,pi,2…,pi,D)。除此之外，每个粒子还知道目前为止整个群体中所有粒子发现的最好位置，这个解是群体极值，记为(gi,1,gi,2…,gi,D)。

PSO算法通过不断迭代完成优化，每次迭代包含速度更新和位置更新两个操作[2]。

(5)

(6)

在式(5)、式(6)中，

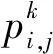
粒子群优化算法具有不依赖于优化问题本身的严格数学性质，具有实现容易、精度高、收敛快等优点；但存在易早熟、易陷入局部最优等缺陷；国内外学者对此进行了大量的研究，并提出了许多改良的方法，主要分为两类：一是对惯性权值的研究，较大的惯性权重能增强全局探索能力, 较小的惯性权重能提高局部发掘能力有利于算法收敛。线性递减惯性权值策略、随机惯性权值策略、自适应惯性权值策略；本文即采用自适应惯性权值策略[4]。

ω=ωini-h·ωh+s·ωs

(7)

(8)

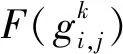
考虑粒子历史最优和全局最优粒子邻域的引导作用，本文引入全局邻域扰动策略[5]。

(9)

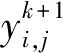
2 相位非线性求解

2.1 计算实例

按照1.2节所述的粒子群优化算法(以下简称PSO算法)设计了Matlab程序，以公式(4)为目标函数，取N=20，D=2，c1=c2=2，ωini=0.9，ωh=0.5，ωs=0.1。以某Ku波段T/R组件41点相位测试数据为例，通过程序计算得到拟合直线(为方便与测试数据对比，拟合直线在±180°处作翻转处理)如图1所示，拟合直线的截距α=7353.344，斜率β=-492.659，计算得相位非线性误差为14.694°。

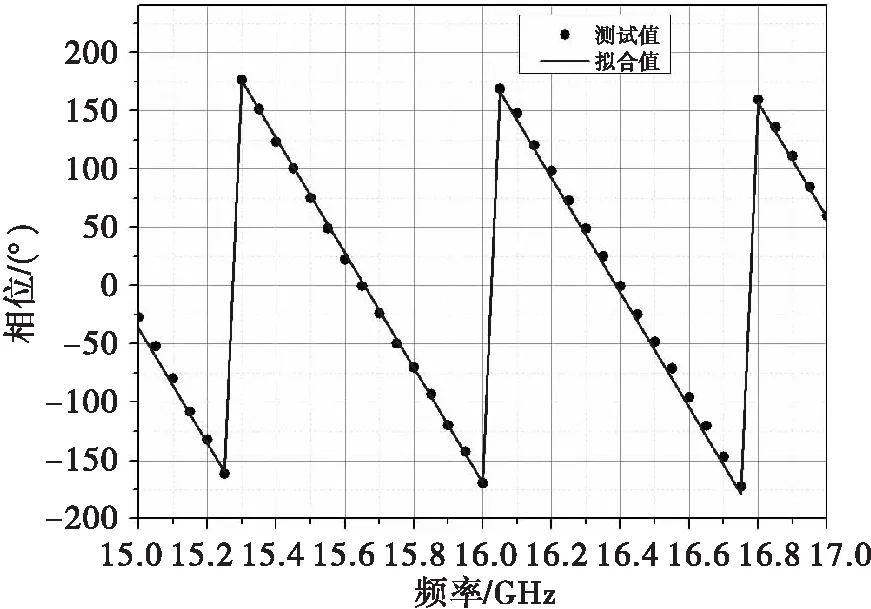
图1 T/R组件相位测试数据及拟合直线

2.2 算法验证

为了验证通过粒子群优化算法拟合直线计算得到的相位非线性误差的准确性，取了10个Ku波段T/R组件的发射和接收链路分别进行了对比，一种通过矢网按1.1节所述方法手动测试相位非线性误差，另一种方法是用PSO算法对传输相位进行拟合计算，对比结果分别如表1和表2所示。表中数据显示发射和接收相位非线性误差的相对偏差分别不到0.16%和0.35%(来源于手动测试误差)，表明计算值和测试值吻合相当好，可以证明PSO算法准确可靠，可以在自动快速测试时采用该算法。

表1 T/R组件发射相位非线性误差(PSO算法)

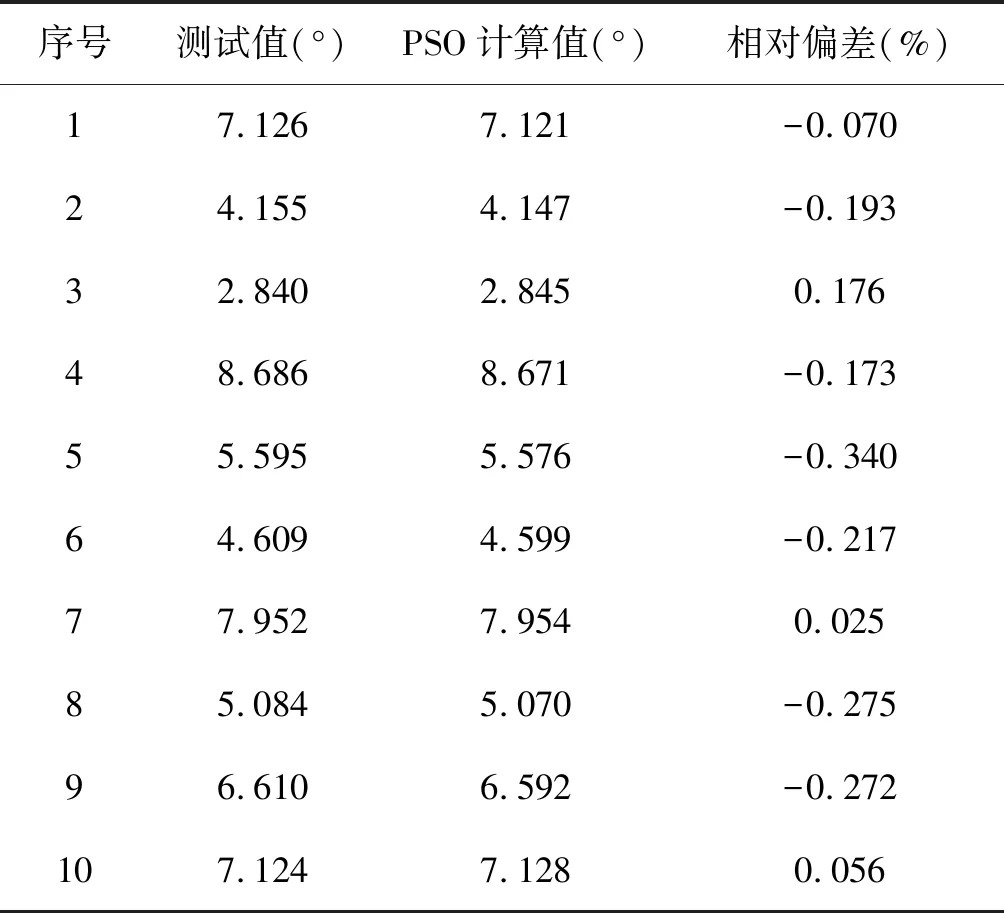
表2 T/R组件接收相位非线性误差(PSO算法)

3 最小二乘法求解对比

用最小二乘法拟合直线(以下简称LSM算法)对2.2节的10组T/R组件发射、接收相位数据进行拟合，得到的相位非线性误差分别如表3和表4所示，可见LSM计算值普遍比测试值偏大，相对误差在0.3%～11.1%之间，由此可见用LSM算法计算相位非线性误差的方法并不准确。

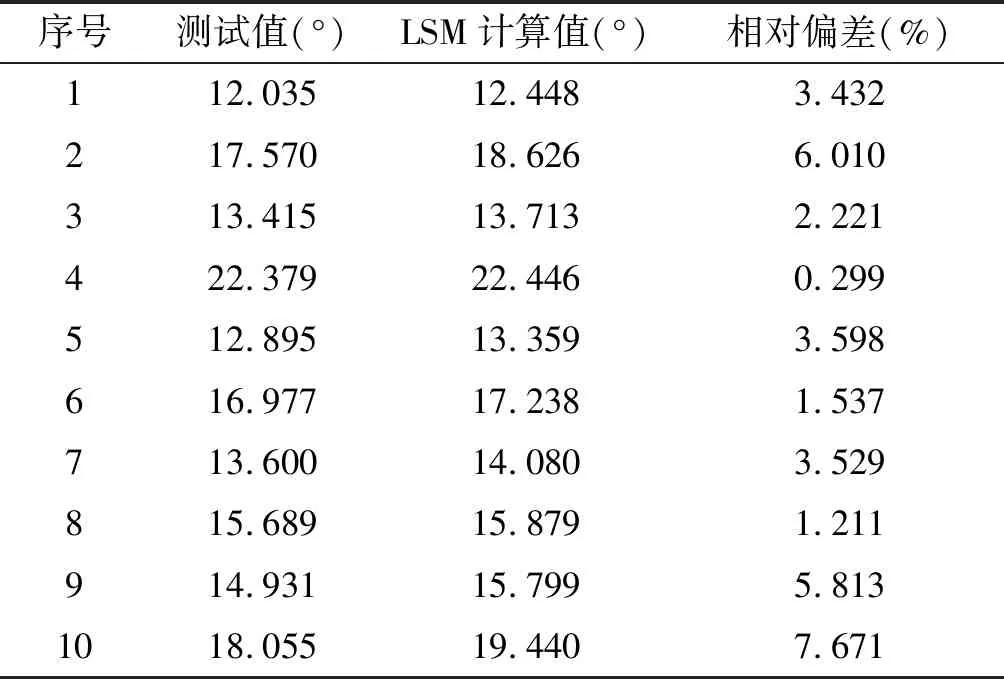
表3 T/R组件发射相位非线性误差(LSM算法)

进一步加大样本数，对PSO和LSM算法计算结果进行对比，如图2和图3所示，分别对2000个T/R组件的发射和接收相位非线性误差进行计算，数据显示LSM算法计算结果总比PSO计算值偏大，相对误差最大能到30.2%。图4和图5给出了相对误差的直方图分布， LSM比PSO算法发射相位相对误差平均10.1%，接收相位相对误差平均6.1%。基于大量数据分析可见，应用LSM算法计算相位非线性误差准确性欠佳，不适合用于T/R组件的相位非线性误差求解。

4 结束语

本文给出了一种应用粒子群优化算法来求解T/R组件相位非线性误差的新方法，实际测试对比表明该算法计算值与测试值吻合非常好，具有准确、可靠、快速等优点，同时通过大量数据对比说明了以往采用的最小二乘法求解方法存在偏差、准确性欠佳。作为T/R组件相位非线性误差这一重要指标的衡量算法，本文给出的PSO算法无疑是一种可以信赖的求解方法。实际上，PSO算法在T/R组件中的应用远不仅此一种，在微波电路阻抗匹配参数优化、滤波器快速设计、SOC芯片参数综合等方面也大有可为。

图2 发射相位非线性误差LSM与PSO对比

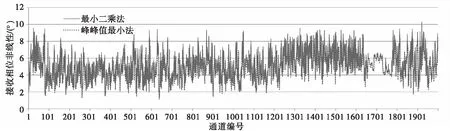
图3 接收相位非线性误差LSM与PSO对比

图4 发射相位非线性误差LSM与PSO相对偏差分布

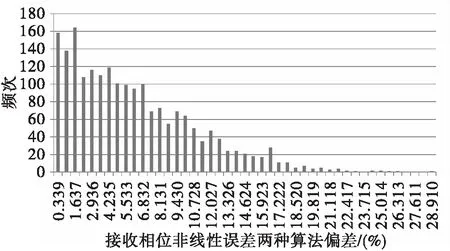
图5 发射相位非线性误差LSM与PSO相对偏差分布