缝槽水压爆破破岩载荷实验研究

夏彬伟，高玉刚，刘承伟✉，欧昌楠，彭子烨，刘 浪

1) 重庆大学煤矿灾害动力学与控制国家重点实验室，重庆 400030 2) 重庆大学复杂煤气层瓦斯抽采国家地方联合工程实验室，重庆400030

✉通信作者，E-mail：liuchengwei12@126.com

随着工程爆破的发展，割缝或刻槽爆破破岩因具有定向控制爆生裂纹、有效控制爆破块径以及工程成本低等优点而得以广泛应用. 但现阶段割缝或刻槽爆破尚使用空气不耦合装药爆破[1−8]，即炮孔间隙介质为空气. 空气不耦合装药爆破时，装药与煤岩体壁面之间存在空隙，爆生气体在该空隙间膨胀做功，消耗爆炸能量，降低了冲击波峰值压力，同时由于空气的可压缩性，推动爆生裂纹后续扩展的准静态压力大小较低、持续时间较短，爆破破断煤岩体的效率不高. 而水压爆破因具有爆炸能量利用率高[9]、易形成“水楔效应”[10−11]、气泡脉动现象[12−13]等优点. 因此将水作为不耦合介质填充于炮孔空隙用以提升缝槽爆破破岩载荷能力，达到高效破断岩石目的，同时减少对非目标围岩的损伤.

在此方面，蔡永乐和付宏伟[14]开展了水压爆破爆炸应力波传播及破煤机理实验研究，提出了一种煤层水压爆破的新方法；朱礼臣和孙咏[15]采用线性不耦合装药和水充填方式爆破开挖沟槽，改善了爆破效果；罗勇等[16]理论上推导了采用不同耦合介质时炮孔孔壁初始压力，并用现场试验表明水压装药爆破能降低粉矿率，提高爆破效率；宗琦等[17]研究了炮孔水压装药爆破时爆炸冲击波的形成和传播，根据弹性理论和波动理论，推导了孔壁岩面正入射的冲击压力；夏彬伟等[18]通过试验分析了缝槽水压爆破形成的裂缝特征及冲击波应力演化规律. 以上研究只是单独地采用实验或理论研究水压爆破的冲击波，而鲜有研究水压爆破准静态压力.

爆破破岩是爆炸冲击波和准静态压力共同作用的结果，但受限于实验条件与使用工况的不同，尚无学者对割缝爆破破岩载荷（冲击波和准静态压力）进行全面的实验研究. 鉴于此，本文开展空气与水两种不耦合介质下缝槽爆破爆炸载荷实验，分析对比空气与水两种不耦合介质下的缝槽爆破冲击波和准静态压力. 对缝槽水压爆破方法的理论及实验基础研究有着积极的意义，为该方法的工程应用提供理论支撑.

1 实验系统及材料

1.1 实验系统

缝槽爆破载荷测试实验系统由爆炸发生装置（自制爆炸腔）、传感器和数据采集仪三个部分组成，如图1所示.

图1 爆破载荷测试实验系统图示Fig.1 Diagram of blasting load test system

1.2 爆炸腔及炸药

为了模拟测定炸药在缝槽中爆炸引起的冲击波以及准静态压力，自主设计制造了缝槽爆炸腔用于实验. 如图2所示，爆炸腔主体材质使用优质碳素结构钢45号钢，其抗拉强度大于等于600 MPa，屈服强度大于等于355 MPa，R表示各孔半径. 爆炸腔主体为高 60 mm，直径 150 mm 的圆柱体，中间构造一个高 20 mm，直径 90 mm，尖端角度 60°的缝槽. 腔体由上下两部分构成，通过12颗M6螺栓进行紧固链接，交界面放置硅胶薄膜，保证上下界面密封性. 为便于装入炮孔不耦合介质和炸药，在爆炸腔上部中心使用M20开口，用M20堵头封闭炮孔. 在缝槽左侧开直径3 mm的通道口，用于传感器安装测量缝槽炮孔内压力. 由火药自制的炸药如图 3所示，ϕ6 mm×20 mm 柱形装药，使用150、200和250 mg三种装药药量，表1为炸药的成分和配比，采用电子点火起爆.

图2 爆炸腔. （a）实物图；（b）结构图（单位：mm）Fig.2 Blasting cavity: (a) physical chart; (b) structure diagram (unit: mm)

图3 炸药实物图Fig.3 Physical chart of explosive

表 1 炸药成分和配比（质量分数）Table 1 Explosive composition and ration %

1.3 传感器及采集仪

爆破破岩的主要动力来源是爆炸产生的冲击波和准静态压力，二者有着较为明显的差异，冲击波载荷比准静态压力大几十至几百倍，但持续时间比准静态压力短几十至几百倍. 为精确测量出爆炸冲击波和准静态压力，分别选用了聚偏二氟乙烯（Polyvinylidene fluoride, PVDF）薄膜压电传感器和压阻式传感器，如图4所示. 厚度为50 μm的PVDF薄膜被制成直径为5 mm的传感器的核心元件，同时薄膜上下面分别放置强度较高且绝缘的聚环氧树脂，主要为了满足绝缘和抗冲击的需要，爆炸使其受压产生电荷信号，通过VIB-1204F数据采集仪转化为电压信号，从而得到冲击荷载；由于空气不耦合爆破和水压爆破的准静态压力相差几十至几百倍，所以选用 0～0.5 MPa 和 0～20 MPa两个量程的压阻式传感器.

图4 两种传感器实物图. （a）PVDF 薄膜压电传感器；（b）压阻式传感器（0～0.5 MPa）；（c）压阻式传感器（0～20 MPa）Fig.4 Physical charts of the two sensors: (a) PVDF neurofibril film piezoelectric sensor; (b) piezoresistive sensor (0 –0.5 MPa); (c)piezoresistive sensor (0–20 MPa)

图5所示为VIB-1204F型超动态数据采集仪，其中VIB-1204F型数据采集卡每个单通道的采样频率可以高达10 MHz，能够精确采集到爆破过程中的冲击载荷及准静态压力变化.

2 实验设计

为探究水压爆破的爆炸载荷特征，验证水介质对爆炸载荷的提升效果，分别开展缝槽条件下水压爆破与空气不耦合爆破爆炸载荷对比测试实验.

实验设计在三种不同药量下，进行水压爆破

图5 VIB-1204F 数据采集仪Fig.5 VIB-1204F data acquisition instrument

和空气不耦合爆破共12组实验，分别测量分析空气介质和水介质下的冲击波载荷和准静态压力特征. 实验组设置如表2所示：

表 2 实验组设置Table 2 Settings of the experimental group

3 实验结果与分析

3.1 冲击压力实验结果与分析

3.1.1 冲击波压力测试结果

由于实验原始数据量较大，每秒包含107个数据点，且原始数据存在一定的干扰噪音，故对实验原始曲线波峰、波谷以及突变处的关键点进行取点作图，并将曲线时间起点归零，便于实验组对比分析，如图6所示. 同时对实验获得的冲击波压力起点、峰值时刻关键点坐标进行记录，如表3所示.

由于缝槽尖端处应力波受波的反射、干涉等影响，以及实验设备存在一定噪音，故#1-1、#2-1、#4-1组实验得到的并非单一应力波的标准“压力−时间”曲线. 但实验测到的冲击波压力峰值和冲击波压力上升沿，仍然根据不耦合介质的不同而具有明显差异.

3.1.2 冲击波压力峰值大小分析

通过对实验获得的冲击波压力峰值（表3）的分析发现，不耦合介质为空气与水时，对于同一不耦合介质，药量的改变对冲击波压力峰值影响不大. 不同三组药量下，空气不耦合爆破中冲击波压力峰值几乎相同，为 8.09±0.18 MPa；水压爆破冲击波压力峰值存在一定差异，但并非随药量增大而增大，应为实验误差所致，其压力为286.28±42.98 MPa.因此进一步的研究中不再考虑装药量大小，而进行不同耦合介质下压力峰值的对比. 实验中炮孔等效半径为 36.5 mm，装药半径为 3 mm，不耦合装药系数为Kd=12.5.

根据赵金昌[19]的研究结果，TNT炸药的不耦合爆破炮孔壁冲击波公式如下所列.

空气不偶合爆破炮孔壁冲击波压力：

水压爆破炮孔壁冲击波压力：

当Kd=12.5，理论上TNT炸药的水压爆破的炮孔壁冲击波压力为空气不耦合爆破的300倍左右；而实验使用的是自制火药，非当量炸药，无法准确计算其理论冲击波压力峰值大小. 实验测得空气不耦合爆破冲击波压力峰值平均值为8.09 MPa，水压爆破冲击波压力峰值平均值为286.28 MPa，可得水压爆破冲击波压力峰值为空气不耦合爆破的35倍左右，虽然未达到TNT炸药理论计算的高倍数，但峰值压力也有明显提升. 表明水作为缝槽炮孔不耦合介质后，冲击压力峰值显著增大.

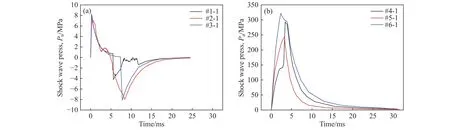
图6 爆炸冲击波“压力−时间”曲线. （a）空气不耦合爆破；（b）水压爆破Fig.6 Pressure−time curve of blasting shock wave: (a) air uncoupling charge blasting; (b) hydraulic blasting

表 3 冲击压力数据关键点坐标Table 3 Key point coordinates of shock pressure data

3.1.3 冲击波特性分析

当冲击波传播到两种不同介质的交界面时，一部分入射波产生了位相角改变180°的反射；另一部分入射波则透射至第二种介质中，如图7所示.

当波在两种不同介质的交界面上垂直传播时，其扰动的边界条件如下：

①在相互作用的任一瞬间，边界两侧的应力必然相等；②边界两侧的正交质点速度必须相等.根据上述条件，可写出如下方程式[20−21]：

式中，σ为波（入射波，反射波，透射波）的应力大小；ρ为介质的密度；C为介质中的冲击波波速；v为对应波（入射波，反射波，透射波）的质点速度.

将公式（3）、（4）、（5）联立可得：

式中，ρ1C1、ρ2C2分别为两种介质的波阻抗，n为两种介质的波阻抗比，F和T分别为反射系数和透射系数.

冲击波垂直传播到两种不同介质交界面时的能量关系为[22−23]：

式中，IR、IT分别为波的能量反射系数和透射系数.

分析公式（7）、（8）可以得出如下结论：

（1）当n→∞,F=1，T=2，反射波和入射波同属于压缩波，形成反射加载，反射波的应力等于入射波的应力，反射波的能量等于入射波的能量，此时介质2受到的应力刚好等于2倍入射波的应力.

（2）当n→1，F=0，T=1，没有反射波，透射波的应力等于入射波的应力，透射波的能量等于入射波的能量并全部进入介质2中，能量传递情况最佳.

图7 波的入射、反射与透射Fig.7 Incident, reflection and transmission of waves

对比不同耦合介质的冲击波“压力-时间”曲线，其冲击压力曲线存在明显不同. 三组空气不耦合爆破的冲击压力在急速上升并回落后又会立刻产生一个大小几乎相同的负应力曲线，这意味着冲击波在到达缝槽炮孔尖端壁面入射的同时，立刻产生了一个与入射波压力大小相同的反射波.而三组水压爆破的冲击压力曲线则与空气组不同，测量得到的整个冲击压力，仅有一个单一的上升与回落过程，说明冲击波在由缝槽尖端面入射时并未产生可以被实验测量到的反射波. 实验得到的结果很好的验证了公式（7）、（8）的分析，即当冲击波由空气入射钢体时，反射冲击波大小基本等于入射冲击波的大小，钢体受到的应力刚好是入射冲击波的2倍，反射波的能量等于入射波能量；当冲击波由水入射钢体时，没有反射冲击波，入射波的全部能量都通过界面进入到了钢体中，这意味着水的波阻抗与钢体相近. 根据李翼祺和马素

贞[21]的研究，岩石的波阻抗约为 7×106kg∙m−2∙s−1，几乎和水的波阻抗相等，所以岩石作为第二介质同样能达到实验效果. 证明水作为缝槽炮孔填充介质，不但能提升到达缝槽尖端炮孔壁的冲击波压力大小，还利于冲击波低损耗入射岩石，将更多的冲击能量用于岩石定向破断.

3.1.4 冲击波压力上升特性分析

通过对实验测得数据上升沿的分析，空气不耦合爆破冲击波上升时间极短，平均在0.25 ms左右，最快的是#3-1实验组，上升时间仅为0.21 ms；而水压爆破的上升沿平均为2.92 ms左右. 由于水的低压缩性，其波阻抗很大，导致爆轰气体在水中的膨胀要比空气中的膨胀慢的多，使形成的水中冲击波波阵面相对空气更“厚”，空气中的波阵面则被压缩得极“薄”，因而波阵面在空气中传播引起前方质点压缩时，其质点速度更大，导致空气不耦合爆破冲击波上升所需时间比水压爆破短.

3.2 准静态压力实验结果与分析

3.2.1 准静态压力测试结果

由于实验过程中存在一定干扰，原始曲线存在一定噪音，对原数据进行1∶1取点，消除噪音点后，得到实验中的爆炸压力曲线图，如图8.

图8 准静态压力取值大小. （a）空气不耦合爆破；（b）水压爆破Fig.8 Value of measuring quasi-static pressure: (a) air uncoupling charge blasting; (b) hydraulic blasting

由于爆炸冲击波存在一个明确的顶点，所以冲击压力的大小可以明确确定，但是在爆炸冲击波后，压力是缓慢降低的，没有明确的时间点确定其为准静态压力，Anderson等[24]和刘文祥等[25]就对准静态压力的取值进行了研究，按照其推荐的方法对准静态压力进行定值：在压力稳定缓慢降低，曲线近似线型，做一条尽量贴近曲线的新的直线，直线反向回推，与波形上升沿交于图8中A～F点，该点的压力值即为准静态压力峰值. 得到实验中6个实验组的准静态压力峰值大小，如表4，表中Pag为空气不耦合爆破的准静态压力实验测量值；Pwg为水压爆破的准静态压力实验测量值.

表 4 准静态压力取值Table 4 Quasi-static pressure values

从实验得到的数据可以看出，缝槽爆破时，水压爆破的准静态压力始终比空气不耦合爆破的准静态压力大，约为空气不耦合装药的37～46倍.以水作为炮孔的耦合介质，炸药能量利用率高，储能作用明显.

3.2.2 准静态压力大小分析

设爆生气体膨胀仍满足理想气体状态方程：

式中，P是气体膨胀压缩过程中的瞬时绝对压力；V是与压力P对应的气体所占体积；γ为绝热膨胀系数，通常取γ=1.3；const表示值为常数.

对于空气不耦合爆炸，炮孔内爆生气体达到准静态平衡时满足：

式中：Pc为爆炸完成时爆生气体压力；rc为装药半径，rc=3×10−3m；Pa为平衡时刻的空气准静态压力；ba为爆生气体径向膨胀量，也是炮孔内原气体径向压缩量.

炮孔内原有气体压力处于准静态平衡时满足：

式中：P0为炮孔内原有气体压力，为大气压力，P0=1.01×105Pa；r0为炮孔内半径，缝槽炮孔的等效内半径r0=3.65×10−2m.

对于水压爆炸，爆生气体达到准静态平衡时同样满足：

式中：Pw为平衡时刻的水准静态压力；bw为爆生气体径向膨胀量，也是水的径向压缩量.

同时根据流体力学理论，水在压缩过程中径向压缩量i和压力P间的关系为：

式中，Ew水的体积弹性模量，可取Ew=2.1 GPa.

公式（13）达到平衡状态时满足公式（14），并积分求得公式（15）：

式中，Ph为静水压力，且Ph=P0.

将实验获得的测量值代入理论推导进行计算验证，由于炸药爆炸完成时刻的爆生气体压力无法测得，将实验测得的空气准静态压力Pa代入式（11）中，即可求得爆生气体的径向膨胀量ba；又将Pa、ba代入式（10）中，即可求得爆炸完成时爆生气体压力Pc；再联立（12）、（15）式，将已知参数代入其中，即可求得水的径向压缩量bw；最后代入（12）式中，即可求得水准静态压力Pw.

将三种药量下的理论推导的计算结果与实验结果对比，如表5，表中Pag、Pwg为实验测量值（相对压力），Pwtg为理论计算相对压力，Pwg/Pag为实测倍数，Pwtg/Pag为理论倍数.

表 5 准静态压力的测量值和理论值Table 5 Measured and theoretical values of quasi-static pressure

通过对比分析水压爆破准静态压力的理论计算值与实验实测值，实验结果与理论推导较为契合，两者共同表明以水作为炮孔的不耦合介质时，炸药能量利用率高，储能作用明显.

3.2.3 准静态压力压降分析

为了分析空气不耦合爆破和水压爆破的准静态压力压降，对实验获得的准静态压力曲线下降段进行拟合，得到6组实验准静态压力下降段的拟合公式，如图9所示.

通过比较，明显可见500 ms时水压爆破比空气不耦合爆破的准静态压力更大，意味着水压爆破的准静态压力保压时间会更长. 这是由于爆炸腔无法做到100%密闭，当准静态压力稳定后，还会有一定泄露，但这恰恰模拟了实际爆破施工中，岩石存在的一些细小原生裂隙，由于空气的滤失系数大于水的，在形成准静态压力阶段后，空气不耦合爆破中气体更容易滤失，形成快速压降.

因而，综合实验中对准静态压力大小和压降的对比分析，可知水压爆破的准静态压力远大于空气不耦合爆破，且水压爆破的准静态压力压降缓慢，保压时间更长. 这是由于水是一种微压缩性介质，当外界压力增至100 MPa时，其密度仅增加5%左右，而相较而言空气的可压缩性强，当炮孔体积一定时，达到平衡时水压爆破的准静态压力远大于空气不耦合爆破. 同时，空气不耦合爆破产生的准静态压力压降速率大于水压爆破，水压爆破保压时间更长，在后续下降阶段水压爆破准静态压力一直保持在一个相对高压的状态，更有利于形成“水楔效应”，楔入裂隙尖端，推进裂隙扩展，形成更大的破断范围，达到更好的爆破效果.并且，爆生气体在水中膨胀速度较空气中慢，压力能均匀和平缓地作用在周围煤岩体上，使煤岩体只产生破裂，而不产生塑性流动和过度粉碎，减少对非目标岩体的损伤，文献[18]中的爆破实物图（图10）也印证了这一点. 如图10所示，试件在空气不耦合爆破后炮孔壁与孔底缝槽完好，无明显破坏痕迹，而试件在水压爆破后，产生了新的裂缝，破断范围更大，且在缝槽壁面形成了片状剥蚀，但未产生粉碎圈.

4 结论

（1）建立了水压爆破载荷测试实验系统，并设计开展了缝槽炮孔条件下水压爆破载荷测试实验，分别测试了空气不耦合爆破和水压爆破的炮孔壁冲击波压力及炮孔内缝槽准静态压力.

（2）水压爆破的冲击波压力峰值远大于空气不耦合爆破的冲击波压力峰值，其峰值约为后者的35倍；由于水和岩石的波阻抗较接近，其冲击波入射效率更高，与理论分析契合度较高；水压爆破的冲击波上升沿相较空气不耦合爆破更平缓，能够使冲击波入射时炮孔壁的质点速度降低.

图9 不同装药量条件下，准静态压力下降段拟合曲线.空气不耦合爆破. （a）150 mg；（b）200 mg；（c）250 mg; 水压爆破：（d）150 mg；（e）200 mg；（f）250 mgFig.9 Quasi-static pressure drop fitting curve under different charge quantity conditions: air uncoupling charge blasting: (a) 150 mg, (b) 200 mg, (c) 250 mg; hydraulic blasting: (d) 150 mg, (e) 200 mg, (f) 250 mg

图10 裂缝细节图[18]. （a）缝槽空气不耦合爆破；（b）缝槽水压爆破Fig.10 Fracture details[18]: (a) slot air uncoupling charge blasting; (b) slot-hydraulic blasting

（3）在不同装药量下，缝槽水压爆破的准静态压力均远大于空气不耦合爆破的准静态压力，其压力约为后者的37～46倍，理论计算结果与实验结果较为契合；水压爆破准静态压力压降缓慢，保压时间更长，为定向裂纹的后续扩展提供更多能量，增加定向断裂范围. 理论与实验结果共同表明了以水作为缝槽炮孔不耦合介质对爆破准静态压力阶段的提升作用.