串联系统的δ-冲击模型及其维修策略优化

成国庆，李 玲

(1.上海海洋大学 工程学院，上海 201306；2.上海立信会计金融学院 统计与数学学院，上海 201209)

0 引言

工程中的多系统在运行过程中会受到外部环境突变的影响，如温度、电流，压力等的突然升高。这些外部因素的变化可能导致系统故障，可将其看作是对系统的冲击。冲击模型是可靠性与维修领域中的一类重要模型，主要研究在冲击环境中系统的生存、故障等特征，并为系统的维护决策提供理论依据。根据冲击导致故障机理的不同，可将冲击模型大致分为[1]：①极端值冲击模型[2](extreme shock model)，单个冲击的强度达到阈值导致系统故障；②累积冲击模型[3](cumulative shock model)，多个冲击的强度累积量达到阈值导致系统故障；③连续冲击模型[4](run shock model)，连续k个冲击的强度都达到阈值导致系统故障；④δ-冲击模型[5](δ-shock model)，连续两次冲击的时间间隔小于阈值δ，导致系统故障。后来，有学者提出了混合冲击模型。如Mallor等[6]研究了累积冲击和连续冲击的混合模型、Wang等[7]提出了δ-冲击和极端值冲击的混合模型，其他混合冲击模型还可见文献[8-9]。

与其他3种冲击模型不同的是，δ-冲击模型关注的是连续两次冲击到达时间间隔而非冲击强度。如某些系统在运行过程中受到谐波电流的影响，导致部件发热，需要一定的时间恢复，若在完全恢复之前又一次受到谐波电流的冲击，则导致部件故障。δ-冲击模型可应用于交通问题、电子器件系统、机械系统、库存管理等多个实际工程领域[10]。

从可靠性分析的角度，Li等[15]在假设冲击达到服从泊松过程的条件下，研究了δ-冲击模型中系统的生存函数，寿命的一、二阶矩及其性质。其后，Li等[11]进一步研究了冲击达到为非齐泊松过程的情形。Eryilmaz[12]研究了冲击到达为波利亚过程(冲击到达间隔不独立)下的系统生存函数及寿命的相关性质。

随着企业竞争的日益激烈，合理的设备维护方案是企业降低运行成本、提高维护效率和生产效益的重要途径[13]。在δ-冲击模型维修决策优化方面，Lam等[14]假设故障阈值和逐次维修时间逐渐增加，对系统的更换策略进行了优化。Wang等[7]考虑了δ-冲击和极端值冲击的混合模型的维修更换问题。Tang等[15]在假设冲击间隔为Weibull分布和Gamma分布的情形下，利用几何过程和更新过程理论对系统的更换策略进行了优化。王小林等[16]考虑了可用度约束下的更换策略。

目前，关于δ-冲击模型维修更换策略的研究对象均为单设备(部件)系统，而在工程实际中，串联系统也广泛存在。如飞机起落架由减震器、收放系统、刹车系统以及转弯系统串联而成，每次降落都可视为一次冲击。机动车的刹车系统由每个轮胎上的刹车装置串联构成，每次刹车就是对刹车系统的一次冲击。再如谐波电流对同一线路上的多个电子设备造成的不良影响也可视为一次冲击。对串联系统而言，由于部件之间存在耦合关系，系统层面的部件最优联合更换策略显然不是各部件最优策略的联合。因此，研究δ-冲击环境下串联系统的维修更换策略优化问题具有理论意义和实际应用价值。本文从经济角度出发，在δ-冲击环境下，利用更新过程理论建立了串联系统长期运行条件下的平均费用率，研究并得出最优联合更换策略的解析求法。最后通过数值实验，验证了本方法并揭示了系统级最优策略与部件级独立最优策略之间的关系。

1 模型描述

1．1 定义

定义1[17]设X，Y是两个随机变量，若对任意实数α，有

P(X>α)≥P(Y>α)，

则称X随机的大于Y，记为X≥stY。若对所有n=1,2,…，满足Xn≥st(≤st)Xn+1，则称随机过程{Xn,n=1,2,…}是随机递减(递增)的。

定义2[18]设{ξn,n=1,2,…}为一非负独立随机变量序列，且ξn的分布函数为Un(t)=U(an-1t)，n=1,2,…，其中a>0，则称{ξn,n=1,2,…}是一个几何过程。

显然，若a>1，{ξn,n=1,2,…}随机递减；若a<1，{ξn,n=1,2,…}随机递增；若a=1，{ξn,n=1,2,…}退化为一个更新过程。

1．2 模型假设

假设1初始时刻，一个由k个不同型部件构成的串联系统开始工作。在工作过程中，系统受到来自外部的随机冲击，其对每个部件均会产生破坏影响。若相邻两次的冲击间隔小于某个部件的故障阈值，该部件发生故障，从而导致系统故障停机。系统故障后，关闭进行维修，不再受到外部冲击的影响。

假设2k个部件的故障阈值分别为δ1,δ2,…,δk。设冲击到达间隔为随机变量τ，若其小于部件i(1≤i≤k)的故障阈值δi(即τ<δi)，则部件i故障。系统故障后立即接受维修或更换，然后重启系统开始工作。冲击的到达服从参数为θ的泊松过程，即冲击间隔τ～H(t)=1-e-θt。

假设4由于修复是非新的，部件i在经历Ni次故障后不再维修，而是更换新的同型部件，假设更换时间可忽略不计。

2 模型建立

本章将建立部件联合更换策略(N1,N2,…,Nk)下的平均费用率模型C(N1,N2,…,Nk)。目标是寻找最优的更换策略(N1,N2,…,Nk)*，使得平均费用率达到最低。

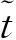
(1)

[0,t]时间段可拆分为各部件的维修时间之和与系统的正常运行时间两部分。故

(2)

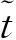
(3)

[0,t]内部件i的维修时间为其更新次数与一个更新期内的平均维修时间之积，即

MTi(t)=NRi(t)·E[TWi(Ni)]

(4)

将式(3)和式(4)代入式(1)，得[0,t]时间段内系统产生的总费用

(5)

将式(3)和式(4)代入式(2)，得总时长

(6)

于是，更换策略(N1,N2,…,Nk)下的系统平均费用率可表示为

(7)

接下来计算式(7)中的两个数量指标：E[MTi(Ni)]与E[TWi(Ni)]。在部件i的一个更新期内，共进行了Ni-1次维修，且逐次维修时间构成随机递增的几何过程，由几何过程定义，有

(8)

由文献[5]可知，对于冲击间隔服从指数分布H(t)=1-e-θt的δ-冲击模型，其首次故障前平均时间为

(9)

(10)

则部件i在一个更新周期内的正常工作时间期望

(11)

将式(8)和式(11)代入式(7)，可得系统平均费用率的解析表达式：

(12)

3 维修策略优化

(13)

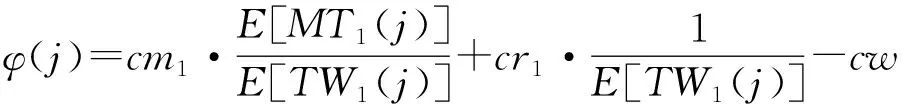
下面将优化C(j,N2)的问题转化为对Aj(N2)的优化，先讨论其单调性。为此，作差：

(14)

式中分母恒为正，其正负取决于分子，构造以下辅助函数：

(15)

则有Aj(N2+1)≥Aj(N2)等价于Bj(N2)≥1。

引理1当φ(j)-cm2ψ(j)<0时，函数Bj(N2)关于变量N2单调递增；反之，Bj(N2)单调递减。

证明Bj(N2+1)-Bj(N2)

(16)

从而，当φ(j)-cm2ψ(j)<(>)0时，Bj(N2+1)≥(≤)Bj(N2)，即Bj(N2)单调递增(减)。

证毕。

当φ(j)-cm2ψ(j)>0时，Bj(N2)单调递减。又

4 实验分析

以某电动机的定子绕组为例，对串联系统的δ-冲击模型最优更换策略进行演示与验证。某三相异步电动机的同心式绕组由两个形状相似但大小不同的线圈按同一个中心位置嵌装而成，是一个典型的两部件串联系统。电动机在运行过程中受到随机谐波电流的影响，谐波电流进入定子绕组时可能会导致附加电能的损失和发热。谐波电流的频繁到达使得定子绕组过热而发生故障。设谐波的到达服从参数为θ的泊松过程，两个线圈的故障阈值分别为δ1和δ2，维修费用分别为cm1和cm2，更换费用为cr1和cr2。各参数值如表1所示(表中费用、维修参数和谐波电流到达率为模拟参数)。

表1 参数设置表

表2 计算结果

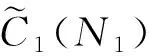
同理有

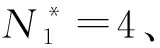
表3 部件1的平均费用率计算结果

表4 部件2的平均费用率计算结果

表5 最优策略对系统参数的敏感度分析结果

由表5可知，对所有参数设置变化情况，系统级的部件联合最优更换策略较各部件独立最优更换策略都要滞后，即系统级的最优联合策略并非各部件最优策略的联合。事实上，在联合决策优化中，每个部件都“让渡”了一定的维修资源(表现为联合最优策略中各部件更换的相对滞后)，才能使得系统整体达到最优。

5 结束语

本文研究了串联系统的δ-冲击模型及其维修更换策略的联合优化问题。系统运行过程中，各部件随着役龄和维修次数的增加而逐渐退化，表现为故障率的升高和维修时间的延长，最终导致部件的更换。以最小化系统平均费用率为目标、以各部件故障次数为联合更换策略，建立了平均费用率的数学模型。在分析费用率函数解析性质的基础上证明了最优联合更换策略的存在性，进一步给出最优策略的求解算法。最后，以典型的串联系统——电动机的定子绕组为例，对本模型和方法进行了验证。敏感性分析结果揭示了系统级的最优联合策略与各部件独立最优策略之间的关系，可为维修管理人员提供决策支持。因此，本文对于企业合理制定维修更换策略、降低运行成本具有一定的指导意义和参考价值。本文假设冲击到达间隔服从指数分布，未来将进一步研究冲击达间隔为伽马分布或威布尔分布，以及更为一般的波利亚过程(到达间隔不独立)的情形，使得模型更加符合实际从而适用范围更广。