考虑通信延迟的多自治水下航行器协同定位算法

卢 健,陈 旭,罗毛欣,杨腾飞

(西安工程大学电子信息学院,陕西西安 710048)

1 引言

多协同体编队结构规划[1–3]、协同定位模型及相关算法设计[4–5]和环境约束下误差建模与补偿[6–7]是水下协同定位(cooperative localization,CL)方法研究的3个主要方向.多自治水下航行器(autonomous underwater vehicle,AUV)协同定位主流是采用“n主带m从”的主从式[8]编队结构,借助于主AUV高精度的自定位信息和主从AUV间相对量测有效改善低自定位水平从AUV的定位精度.相比于基于优化理论[9]和基于图论[10]的算法,基于Bayes估计的协同定位算法由于能够有效地融合被定位体内外部定位相关信息[11],成为了主流方法.作为一种重要的Bayes滤波器,扩展卡尔曼滤波(extended Kalman filtering,EKF)具有计算量小、易于工程实现等特点,特别适宜处理处于水下环境的AUV的定位问题.文献[12]提出了一种基于EKF的多AUV主从式协同定位方法,仿真验证了这种基于概率学方法的有效性.文献[12]的方法本质是一种基于整周期滤波的算法,本文的研究中将其作为基础算法并进行改造,同时将其作为仿真分析的对比方法.

在误差的建模与补偿问题中,根据环境约束条件优化协同定位算法或改善协同编队结构[13]是建构有效的误差在线估计模型和补偿算法[14]重要保证.水下环境使用声信号作为载体进行信息传输为最有效手段.水声通信有两个基本任务:形成测量值和传递状态信息.量测的生成是利用水声传播时延(time-of-flight,TOF)原理:

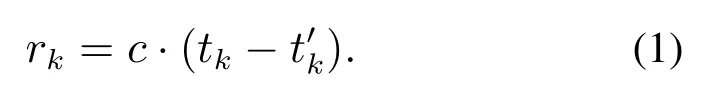
声信号的发送端和接收端必须使用同一时钟或已同步的不同时钟. c为声波在水中的传播速度,和tk分别为主AUV发送探测脉冲信号和从AUV接收到此脉冲信号的时刻.

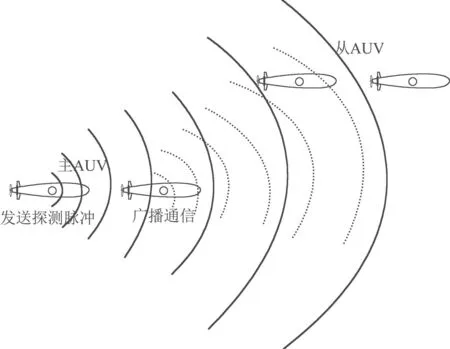
图1 主从AUV间的水声通信Fig.1 The underwater acoustic communication between the master and the slaver AUV

实际中,主AUV发射的探测脉冲信号和传送状态信息的通信数据包一般由不同装置产生,并且,为了避免造成相互干扰,将二者进行分时发射.如图1,单周期内AUV间水声通讯信号的发射过程须分两步:第1步发射用于形成量测的声脉冲信号;第2步延迟一个足够小的随机时间,发射含有脉冲信号发送时刻的主AUV运动状态信息的通信数据包.除了水声传播时延之外,由于水下环境复杂性导致的水声多径传播、传感器的固有延迟和信号在器件内部的处理与传输延迟等原因,脉冲串和通信数据包的传送过程都存在一定的固有和随机延迟,而且通信数据包信息由于丢包、数据解构和传送带宽限制等原因,延迟时间会更长.

如何减小通信延迟对提升协同定位精度的不利影响是环境约束下误差建模与补偿研究的重点问题.文献[15]提出了在从AUV量测信息接收时刻利用新息对估计误差进行补偿的方法,但是该类方法需要存储器对延迟时间内的估计状态进行保存,并要求对量测信息进行时间上的排序,增加了定位系统的负担.文献[16]通过建立一个主AUV运动状态估计器,在状态信息延迟的条件下,实时完成了协同定位,降低了对硬件存储的要求.但是其对出序的通信数据包采取了丢弃的做法,没有充分利用信息,损失了精度.

按照信息是否能够以其所产生的时间顺序到达定位系统,通信延迟分为信息顺序到达和信息出序到达两种情景.虽然没有出序,但是延迟了的顺序信息依然会造成估计精度的降低或实时性变差.设计一种更适合处理本类延迟信息的协同定位方法是本文所建立的关于通信延迟协同定位算法体系的重要一环.信息发生出序是通信延迟所带来的一个严重后果.信息出序可能造成出序信息不能够被使用或者高成本被使用.使用Bayes滤波器时,对于出序信息的处理方法文[17]中有多种:①丢弃滞后数据法:简单易行且计算量小,但大量数据弃用会严重降低定位精度;②数据缓存法:精度高,但需要大量存储空间缓存数据,滤波器输出滞后;③重新滤波法:最终精度及存储要求与数据缓存法相同,造成重复滤波,实时性差;④直接更新法:利用出序信息直接在最新采样周期内进行状态更新,存储量和计算量都很小,滤波输出没有滞后且精度较高,实时性强.

在发生信息出序时,如何平衡高精度估计值对数据缓存的需求与运动系统输出实时性要求之间的矛盾,是水下协同定位一个亟待解决的难点问题.本文建立了水声探测和水声通信的时延模型,给出了AUV的运动学模型和水声量测模型,在提出延迟信息顺序到达算法的基础上,重点研究如何采用直接更新的方法解决信息出序到达时的主从式协同定位问题.本文建立了一类全新的针对水声通信延迟的协同定位算法,其优先保证实时性,不缓存量测数据和中间结果,估计结果具有较高的精度.

2 水声探测和通信时延模型

除了水声传播时延,脉冲串和通信数据包发送与接收过程中的滞后时间还有:

1) 脉冲串发送端的固有时延.即声脉冲信号从开始启动发射(kT时刻)到物理设备真正发出信号的时间.此时延极短,且为固定时延.

2) 脉冲串处理时延.即声脉冲被接收后对其进行处理的时间,包括信息在从AUV内部的传输和形成量测值的时间.此时延相对较短,但为随机时延.

3) 通信数据包的发射时延.在探测脉冲启动发送之后,延迟一个较小的随机时间,才发射含有脉冲串发送时刻的主AUV运动状态信息的水声通信数据包.此时延相对较短,为随机时延.

4) 通信数据处理时延.此时延包括通信数据包被发送、被接收、被解析和被重构以及在从AUV内传输的时间.此时延相对较长,为随机时延.本时延占用较长时间的一个重要原因是需要对多径传播的大信息量的数据进行处理.

根据以上分析,建立水声探测和水声通信的时延模型.

探测时延:

其中:τa为探测脉冲串水声传播时延,τb为脉冲串发送端的固有时延,τc为脉冲串处理时延;τα为通信数据水声传播时延,τβ为通信数据的发射时延,τγ为通信数据处理时延.

用各种时延对水声探测和水声通信过程进行分解后,对于信息的到达可做如下界定:

1) 脉冲串到达AUV时刻.即从AUV接收到脉冲的时刻.从AUV根据本时刻与脉冲发出时刻获取τa,并根据式(1)计算出量测值;

2) 脉冲串到达滤波器时刻.此时接收AUV已解算出量测值,并可以被协同定位算法使用.此时刻与脉冲串到达AUV时刻相差一个τc;

3) 状态数据到达滤波器时刻.此时通信数据包含有的状态信息已被解析为可被滤波器直接使用的数据,一般情况下,通信数据包延迟到达时间明显长于脉冲串延迟到达时间.从发射脉冲串开始,到此时刻正好经历整个通信延迟时间τcom.

通信数据包中的主AUV的状态信息的时戳界定为真正发出脉冲串的时刻;通信数据包中含有的关于主AUV的状态信息,主要为主AUV的本体传感器在此时戳点对自身位置的观测信息和推算结果.从AUV的运动状态更新点的时戳为脉冲串到达时刻,由从AUV记录本时刻,并于通信数据包到达后在本时戳点更新运动状态的估计值.时延的随机性增加了考虑通信时延的协同定位问题的复杂度.

由于探测脉冲的时延较小,所以本文将研究重点放在通信数据包时延对定位精度的影响和补偿问题上.

3 运动学和量测模型

3.1 AUV运动学模型

由于深度信息可由压力传感器直接测得,则定位问题的研究可以由3D空间中转化至2D平面内.其运动轨迹可在oxy坐标系下进行描述,如图2所示,k时刻的位置可表示为(xk,yk).

图2 AUV运动状态量简图Fig.2 The diagram of the motion state of AUV

AUV运动学模型可表述为

其中:T为AUV的采样周期,Vk,ϕk为AUV在k时刻的运动速度和偏航角.

控制向量表述为

由于本文重点考虑延迟时间与定位精度的关系问题,所以在AUV的运动学模型中加入推算时间T:

3.2 量测模型

两AUV每隔时间T进行一次协同定位,由从(salver)AUV解算出的其与主(master)AUV的相对距离可表示为

Rk是误差协方差.

量测模型可简单地描述为

4 信息顺序到达协同定位算法

为研究简便,设环境中只存在一个主AUV,相邻时刻主AUV发送的脉冲串与通信数据包可按照顺序到达从AUV的滤波器.

如图3所示,尽管第k个周期内的主AUV的通信数据包在k+1个周期才到达从AUV的滤波器,但还是早于第k+1个周期主AUV发送的通信数据包到达,通信有延迟但没有出序.从AUV的运动状态估计应在k周期内tk时刻和k+1周期内tk+1时刻完成.根据时延的定义和模型,图中时间含义及关系为

其中:t1为主AUV发送出脉冲串的时刻,tk为从AUV接收到脉冲串的时刻,t1+τβ为主AUV发送通信数据包的时刻,为通信数据包到达从AUV滤波器的时刻.以对k周期内从AUV定位为例,协同定位算法如下.

图3 信息顺序到达时序Fig.3 Information sequential arrival Timing

根据水声传播时延公式,相对距离量测值为

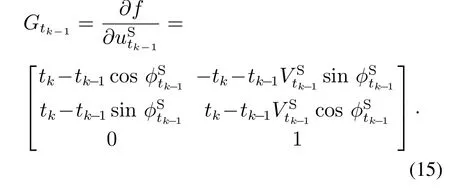
使用tk时刻传感器量测更新系统状态,利用从AUV的tk时刻状态预测和主AUV的t1时刻状态估计(此值由时刻从AUV接收到的通信数据包所提供)对量测值的估计为

从式(20)–(21)分别得出从AUV的运动状态估计值和对估计结果的评价.对于此类有信息延迟但没有出序的情景,本文提出的序贯处理算法可以在延迟时间可预计的条件下得到最优的估计精度.

5 信息出序到达协同定位算法

如图4所示,相邻时刻主AUV发送的通信数据包未按照顺序到达从AUV的滤波器.第k和k+1个周期中主AUV在t1和t2时刻所发送的脉冲串按照发送顺序依次在tk和tk+1时刻到达从AUV;含有主AUV在t1和t2时刻位置状态的通信数据包分别于时刻到达从AUV的滤波器,时刻早于时刻,通信数据包出序到达.

5.1 信息出序问题分析

为了能够维持较高的定位精度,协同定位要求从AUV在通信数据包可用时立即利用主AUV运动状态数据和量测,完成对从AUV位姿状态估计的更新.如图4,就是要估计tk和tk+1时刻从AUV的运动状态.按图4中信息发生出序到达,第k+1个周期的协同定位所需数据在时刻先完备,先对tk+1时刻从AUV的运动状态进行估计;而在时刻第k个周期的协同定位所需数据才完备,但此时从AUV状态已经更新至相对于tk时刻更晚的tk+1时刻,如果使用常规的协同定位算法,将无法再利用tk时刻的数据对从AUV的运动状态进行更新,致使这部分信息无益于对定位精度的改善.

理论上,出序的情景有3种类型:1)脉冲串顺序到达,通信数据包出序到达,如图4;2)脉冲串出序到达,通信数据包顺序到达,如图5;3)脉冲串和通信数据包都出序到达,见图6.情景2与情景1相类似,都属于量测后形成而数据先完备的情况;对于类似情景3的类型,由于先形成的量测对应的数据也先完备,可以应用第4节中算法予以应对.

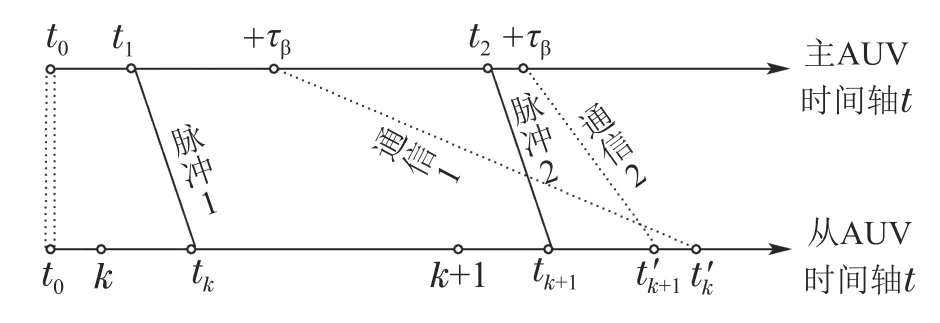
图4 信息出序到达时序1Fig.4 Information out-of-sequence arrival Timing 1

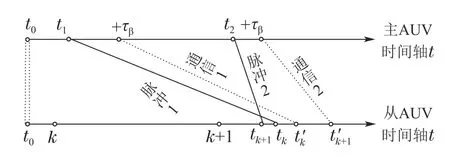
图5 信息出序到达时序2Fig.5 Information out-of-sequence arrival Timing 2

图6 信息出序到达时序3Fig.6 Information out-of-sequence arrival Timing 3

相比于脉冲串,通信数据包信息量大且传输过程复杂,通信延迟时间长,更容易出序,以图4所展示的情景为背景进行分析和提出解决方案将更有现实意义.信息出序导致较晚时刻产生的信息反而先于较早时刻产生的信息被使用,而当较早的信息可以被使用时,从AUV的状态估计值已经被更新至较晚时刻.出序信息处理的实质就是将这些较早产生的信息有效加以利用来提高定位精度.在接下来的工作中,本文将试图建立一种全新的协同定位算法,其基本思路为:不存储任何量测和滤波中间结果,在出序量测可用时,将其用于在最新状态估计时刻对状态估计值进行再更新,优化协同定位精度,从而达到兼顾系统输出实时性和对信息的无损利用以最大限度地提高定位精度的目的.

5.2 AUV运动模型的线性化

AUV运动过程中其本体传感器测量的不准确性反映了过程噪声影响.为适应后续算法推导的需求,在通信延迟周期内,将AUV运动模型进行线性化表示,显式化明确过程噪声.

AUV的航位推算模型如式(6),则有

其中:Ik为单位阵;Vmk和ϕmk为AUV实际运动速度和偏航角,可用延迟周期内多次测量的平均值近似,当AUV稳定航行时,短时间内可认为其为固定值.则设

5.3 出序问题的解决方案

假设从AUV运动的初始时刻、过程噪声和量测噪声之间互不相关.为了叙述简便和后续推导过程的清楚,将除了出序量测外的所有量测形成时间点(即各时刻脉冲串到达时刻)设为t1,t2,···,tk−1,tk,并假设形成于时刻td的量测zd为l步滞后,即

5.4 信息出序到达的协同定位算法

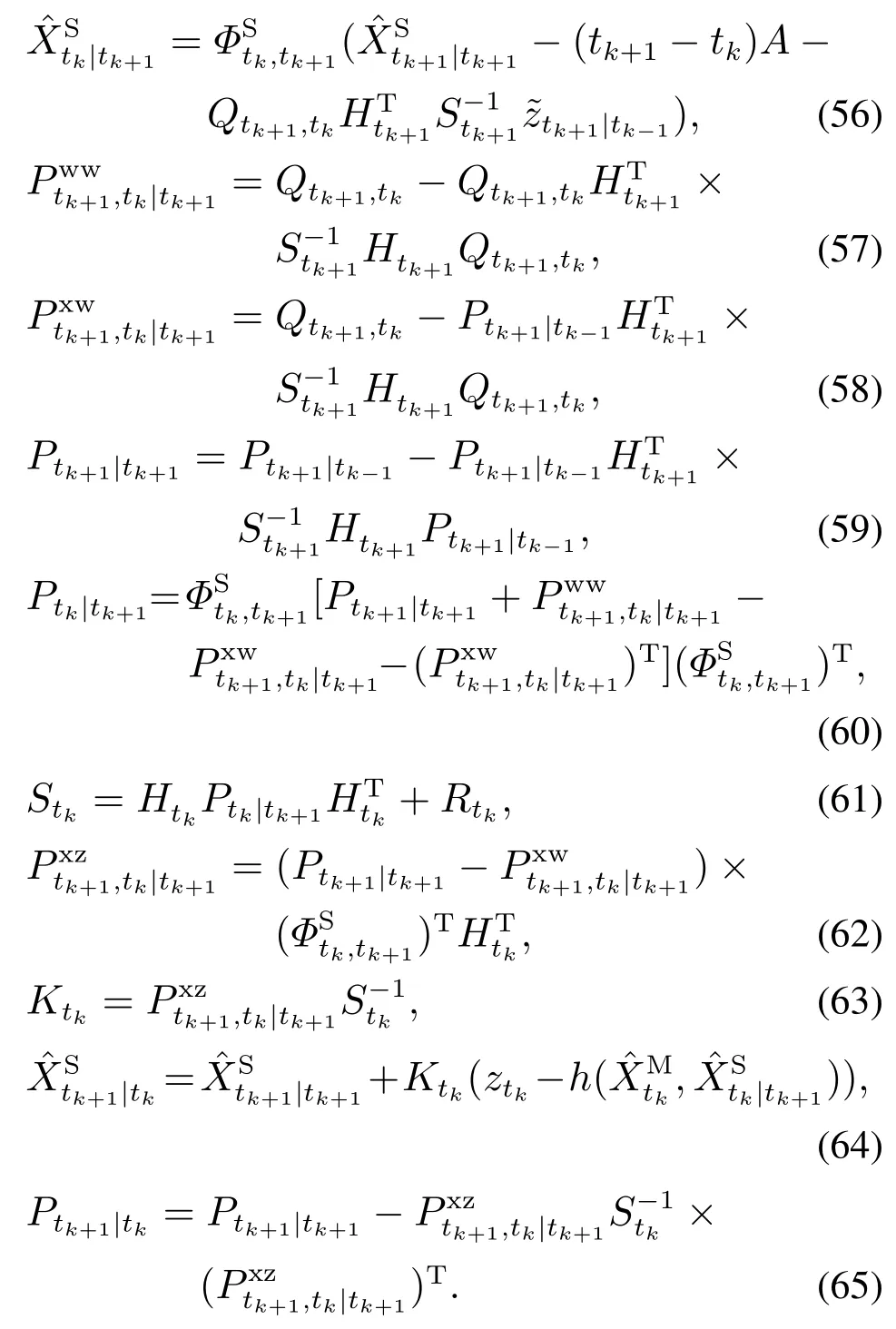
5.5 “n主带m从”模式信息出序问题的讨论

在多主多从的“n主带m从”模式下,对于m从中的每一个个体来说,只需要接收每一个主AUV发送的信息并将其用于自身的状态更新即可,不需要与m中其他个体交互.所以,从信息的角度看,“n主带m从”模式实质为若干个“n主带1从”模式的不相关组合.对于“n主带1从”模式,由于一般情况下n个主AUV相距有一段距离,与从AUV的距离差别较大,系统设置的采样间隔较大,故而多考虑信息在一个周期内出序的情景.当某一主AUV发送的数据出序时,按照数据后完备后处理的原则,依照第5.4节算法,利用其在最新状态估计时刻对状态估计值进行再更新.

6 仿真分析

为了更好地比较和分析,设定主从AUV距离一近一远两种情景,图7–8显示了二者沿着各自方向从左向右运动的真实轨迹关系.设定主AUV拥有较高的自定位精度,其本体传感器噪声较小:

从AUV的本体传感器噪声较大:

二者运动速度均为10 kn.主AUV定时发送声信号(含脉冲串和状态数据包)给从AUV,设定脉冲串发送固定延时为0.1 s.设定水声传播速度c=1500 m/s.为了表述简单,以下将信息顺序到达协同定位算法简称为延迟算法1.0,将融入信息出序到达处理方法的协同定位算法简称延迟算法2.0.为了说明仿真结果的科学有效性,进行了1000次Monte Carlo仿真.

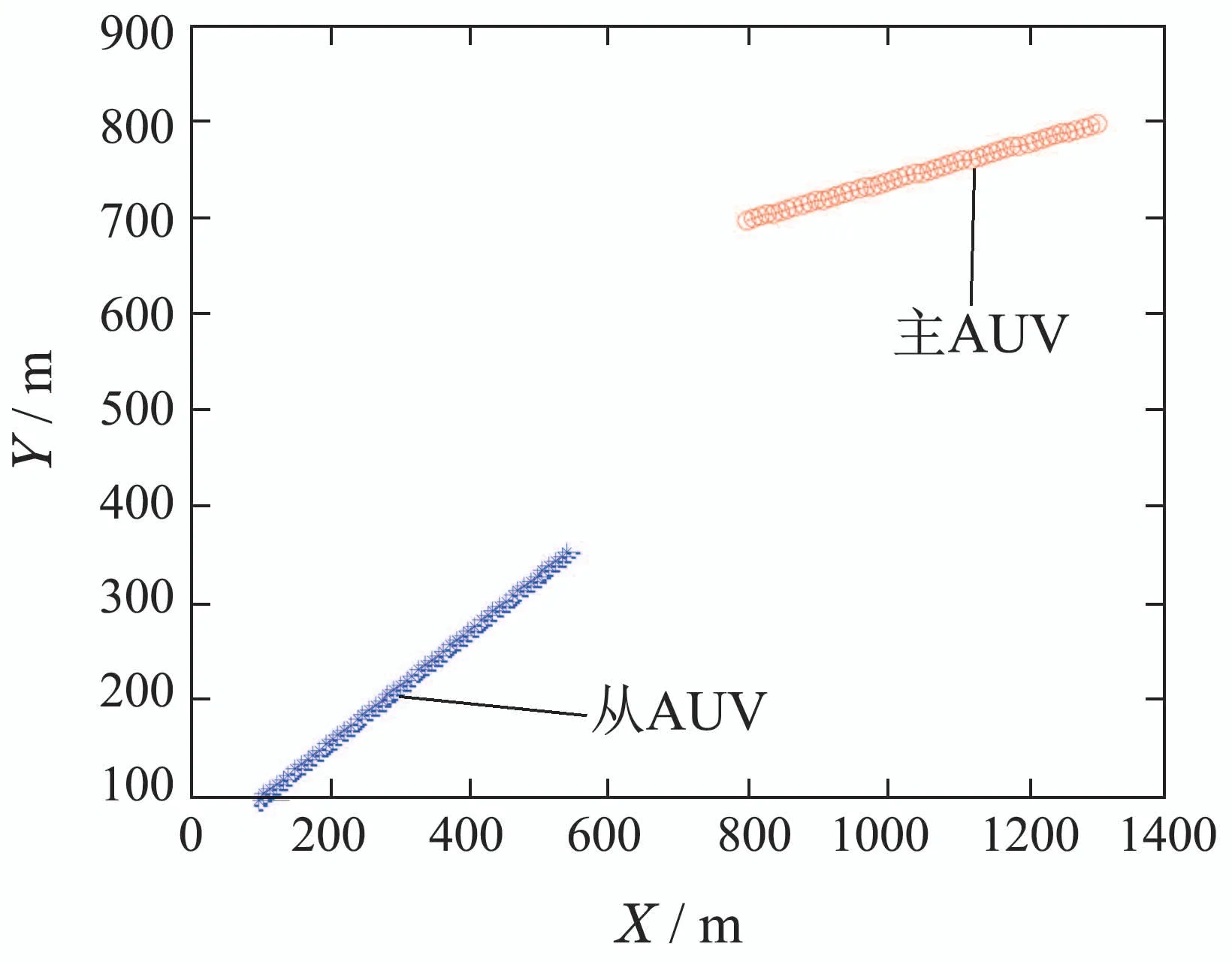
图7 两AUV的实际航行线路1Fig.7 The actual navigation route 1 of two AUVs

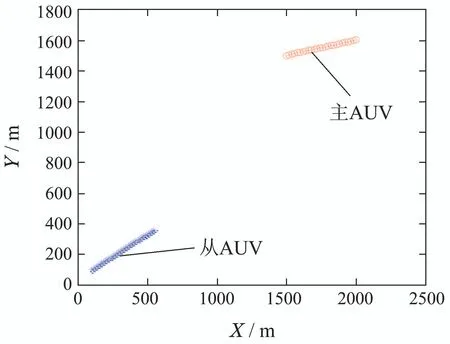
图8 两AUV的实际航行线路2Fig.8 The actual navigation route 2 of two AUVs

6.1 信息顺序到达情景的仿真分析

类似图3情景,设定量测和通信数据包能够按顺序到达从AUV.采用3种方法估计从AUV的航行轨迹:①航位推算,即只采用本体传感器和运动模型来估计位置;②整周期滤波算法,即利用本周期量测和数据包在整周期时间点更新从AUV状态;③延迟算法1.0.

针对图7情景,设定采样周期为2 s.设置3种声纳传感器探测噪声水平如下:①σr=5 m;②σr=10 m;③σr=15 m.各噪声水平下各算法的估计结果的均方根误差(root mean square error,RMSE)比较如表1.相应的比较估计误差均值和方差如图9,其中柱状图为误差均值,线棒为估计误差的方差.在①的噪声水平下,各算法从AUV的位置估计误差比较如图10.

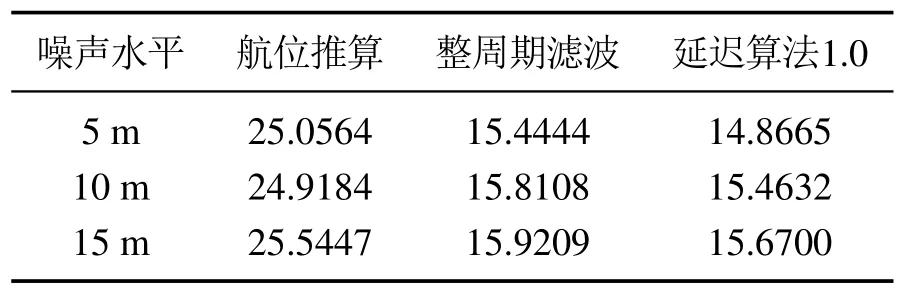
表1 主从AUV近距离情景不同噪测探声水平下各算法估计结果的RMSE(m)Table 1 The RMSE of the estimation results of each algorithm at different tetecdion noise levels in the short-distance scene of the master-slaver AUV(m)

图9 主从AUV近距离情景不同测量噪声水平下的误差均值和方差比较Fig.9 Comparison of the Mean and Variance of errors at different measurement noise levels in the short-distance scene of the master-slaver AUV

图10 主从AUV近距离情景噪声水平①各算法从AUV的位置估计误差比较Fig.10 Comparison of location estimation errors in each algorithm at the noise Level ①in the short-distance scene of the master-slaver AUV

针对图8情景,设定采样周期为4 s.设置3种声纳传感器探测噪声水平如下:①σr=10 m;②σr=15 m;③σr=20 m.估计结果的RMSE比较如表2.相应的比较估计误差均值和方差如图11.在①的噪声水平下,各算法从AUV的位置估计误差比较如图12.

表2 主从AUV远距离情景不同探测噪声水平下各算法估计结果的RMSE(m)Table 2 The RMSE of the estimation results of each algorithm at different detection noise levels in the long-distance scene of the master-slaver AUV(m)

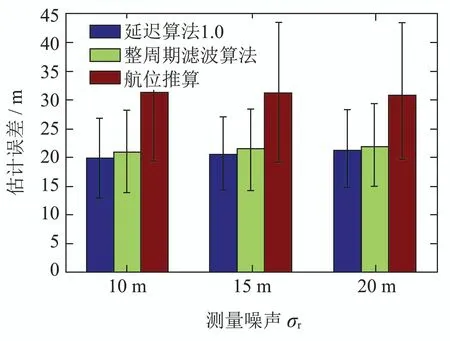
图11 主从AUV远距离情景不同测量噪声水平下的误差均值和方差比较Fig.11 Comparison of the mean and variance of errors at different measurement noise levels in the long-distance scene of the master-slaver AUV

图12 主从AUV远距离情景噪声水平①各算法从AUV的位置估计误差比较Fig.12 Comparison of location estimation errors of the slaver AUV in each algorithm at the noise Level ①in the long-distance scene of the master-slaver AUV

表1–2、图9和图11都显示了两种不同的距离尺度下,不同探测噪声水平下3 种估计方法对从AUV位置估计效果,以EKF为核心算法的协同定位算法对于误差的抑制能力远优于航位推算方法,本文提出的延迟算法1.0采用序贯量测处理的方式,在不提高算法复杂度的基础上,相比于常规整周期滤波的协同定位方式,能更进一步提升定位精度.相比于图10,图12所反映的是大距离尺度情景各算法的估计效果,在主从AUV距离较远时,量测延迟时间会更久,相比其他方法,本文所提出的方法会更有效.无论是图10或是图12中,延迟算法1.0与经典的整周期滤波算法的估计误差曲线变化趋势相同,具有较好的一致性.

6.2 信息出序到达情景的仿真分析

设定通信数据包可能出序到达,出序时类似图4情景.采用4种方法估计从AUV的航行轨迹:①航位推算;②量测丢弃算法;③数据缓存算法(由于重新滤波算法的最终滤波精度与本算法相同,估计结果等价,则在本实验中不做重新滤波算法估计过程仿真.);④延迟算法2.0.

针对图7情景,设置3种声纳传感器探测噪声水平如 下:①σr=5 m;②σr=10 m;③σr=15 m,采样周期为2 s.为了更清晰地展示本文算法效果,假设主从AUV间每2次通信中有一次通信数据出序到达的现象发生,即设定2,4,6,···等周期内的通信数据迟于相邻的3,5,7,···等周期内的通信数据到达,并可在3,5,7,···等周期内到达,可以利用其进一步更新从AUV在3,5,7,···等周期内的运动状态.估计结果的RMSE比较如表3.相应的比较估计误差均值和方差如图13.在③的噪声水平下,各算法从AUV的位置估计误差比较如图14.

表3 不同探测噪声水平下各算法估计结果的RMSE(m)Table 3 The RMSE of the estimation results of each algorithm at different detection noise levels(m)

表3和图13显示了小距离尺度3种不同探测噪声水平下4种估计方法对从AUV位置估计的效果.数据缓存算法的估计精度最高,本文提出的延迟算法2.0优于量测丢弃算法和航位推算.数据缓存算法(重新滤波算法)虽然有较好的抑制误差能力,但是需要等待数据完备后回到先前时刻对估计状态进行更新,牺牲了实时性,且需要存储空间缓存数据;延迟算法2.0属于直接更新法,虽然在出序时刻无法利用外部量测修正航迹而导致定位精度有所下降,但可在出序量测可用时,在最近状态更新点利用其迅速改善定位精度,有效收敛定位累积误差,达到为快速运动的AUV实时提供高精度定位信息支持的目的.图14比较了小距离尺度下4种算法的位置估计误差,本文所提出的算法估计精度介于数据缓存算法和量测丢弃算法之间,说明了通过设计算法,将发生通信延迟时的信息加以利用而不是丢弃对提升定位精度具有重要意义.

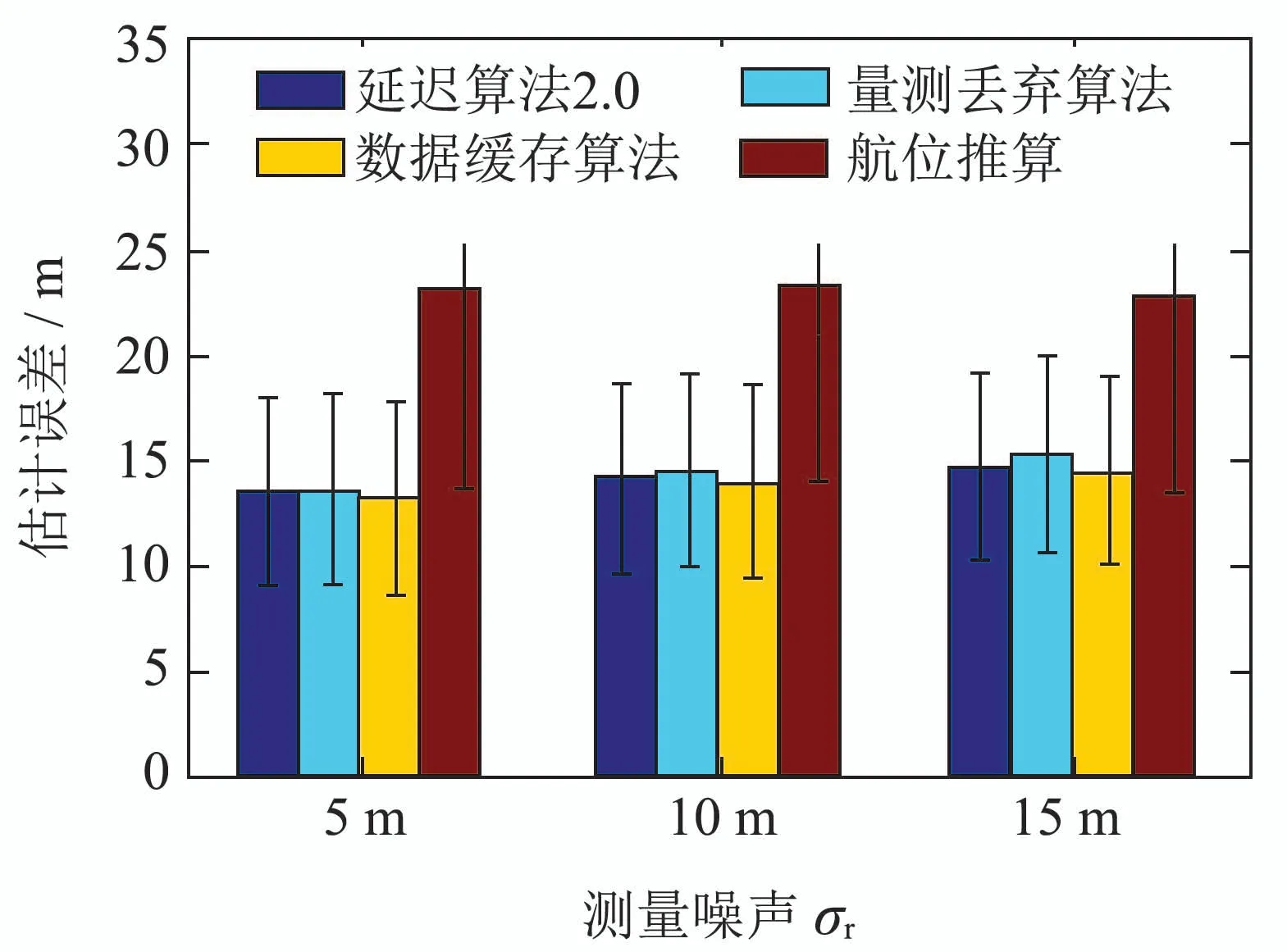
图13 不同测量噪声水平下的误差均值和方差比较Fig.13 Comparison of the mean and variance of errors at different measurement noise levels

图14 噪声水平③各算法从AUV的位置估计误差比较Fig.14 Comparison of location estimation errors of the slaver AUV in each algorithm at the noise Level ③

表4 不同出序情景下各算法估计结果的RMSE(m)Table 4 The RMSE of estimation results of each algorithm in different out-of-sequence scenarios(m)

针对图8情景,设定声纳传感器探测噪声σr=20 m,采样周期为4 s.设置3种信息出序情景:①每2次通信中有一次信息出序;②每3次通信中有一次信息出序;③每4次通信中有一次信息出序.估计结果的RMSE比较如表4.相应的比较估计误差均值和方差如图15.3种出序情景各算法从AUV的位置估计误差比较如图16–18.

图15 不同出序情景下的误差均值和方差比较Fig.15 Comparison of the mean and variance of errors in different out-of-sequence scenes

图16 情景①各算法从AUV的位置估计误差比较Fig.16 Comparison of location estimation errors of the slaver AUV in the Scene ①

图17 情景②各算法从AUV的位置估计误差比较Fig.17 Comparison of location estimation errors of the slaver AUV in the Scene ②

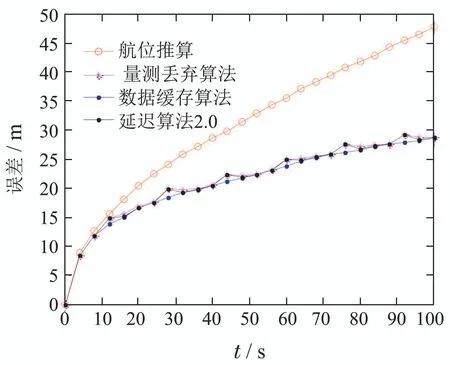
图18 情景③各算法从AUV的位置估计误差比较Fig.18 Comparison of location estimation errors of the slaver AUV in the Scene ③

表4和图15显示了大距离尺度相同水平探测噪声3种信息出序情景条件下4种估计方法对从AUV位置估计的效果.比较每一种出序情景对应延迟算法2.0和量测丢弃算法的RMSE和误差均值可以看出,随着出序频次的降低,两种算法的RMSE和误差均值差值越来越小,这一点与图16–18所显示的曲线差别度一致.比较图16–18中的各算法的估计误差曲线,延迟算法2.0的估计误差曲线始终介于量测丢弃和数据缓存两种经典算法的曲线之间,且在出序信息加以利用后,延迟算法2.0估计误差曲线迅速回归于数据缓存算法估计误差曲线,曲线的总体变化趋势相同,具有较好的一致性.为了更好地说明本文算法的有效性,给出与图16相对应的,在各延迟信息到达时刻,融入延迟信息前后的从AUV的位置估计误差比较,如图19所示.

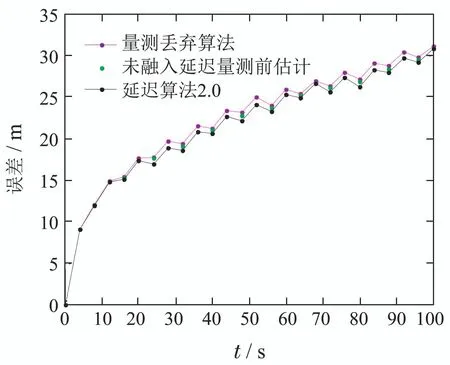
图19 融入延迟信息前后的位置估计误差比较Fig.19 Comparison of estimation errors before and after integrating delay information

图19中粉色曲线对应着始终放弃使用延迟量测更新从AUV运动状态的位置估计误差,绿色离散点标示只利用当前时刻量测更新从AUV运动状态(按算法程序,延迟算法2.0先利用本时刻量测信息)的估计误差,而对应的黑色点标示将上一时刻所产生的、于本时刻才到达的延迟量测信息进一步用于状态更新后(延迟算法2.0后利用出序信息)的估计误差.表5与图19对应,给出了各延迟量测可用时刻状态估计过程中融入延迟信息前后的估计误差值.从表5中可以看到,在每一时刻,融合了延迟量测的延迟算法2.0都进一步减小了估计误差.以上说明了在出序信息可用时,延迟算法2.0可以迅速地以一定幅度提升协同定位的精度.

表5 融入延迟信息前后估计误差值(m)Table 5 Estimation errors before and after integrating delay information(m)

7 结论

如何减小通信延迟对协同定位过程中定位精度和实时性的不利影响是一项重要又富有挑战性的工作.本文分析了水声信息传输的复杂过程,建立了水声探测和水声通信的时延模型,对主从式协同结构的信息顺序到达和出序到达情景做出了描述和分析,设计了2种适用于处理延迟信息的多AUV协同定位算法,并进行了仿真实验分析.本文验证并得出了如下结论:

1) 对于有延迟但没有出序的顺序信息,本文提出了一种将信息序贯处理的信息顺序到达协同定位算法,相比于航位推算、整周期滤波等传统方法,可以较明显地提升定位精度.

2) 本文的主要创新点和贡献是针对信息出序情景,提出了一种直接使用出序信息优化当前时刻状态估计值的方法.相比于量测丢弃等方法,由于没有损失信息而具有更高的定位精度;相比于数据缓存等算法,不需要缓存数据,滤波器输出无滞后,实时性好.

3) 本文算法与经典协同定位算法具有相同的定位估计一致性,能够有效抑制误差发散速度.在具有较好的理论意义的同时,也具备工程实践参考价值.