森林环境下的无人直升机安全飞行控制

梅 蓉

(南京森林警察学院 侦查学院，南京 210023)

森林被称为地球之“肺”，对人类和野生动物的生存至关重要.我国森林面积高达2.08亿公顷，因而森林防火工作是我国防灾减灾工作的重要部分，也是我国公共应急体系建设的重要内容[1].近几年来，国内外森林火灾频发，造成了大量的财产损失，甚至付出了包括消防员在内的诸多生命代价.森林火灾发现和扑救难度大，必须防患于未然.无人直升机凭借着成本低、易操纵、反应快速和机动灵活等优势，可监测到地面巡护无法涉及到的偏远地区的林火，并将现场火灾信息实时发送到指挥中心，从而识别林火并发出警报，实现超视距和夜间巡护等[2].因此，无人直升机在森林火灾监控方面有很好的应用前景.但森林环境中高低不同的树木会导致风场发生动态突变，给无人直升机的飞行安全带来潜在的威胁，需要发展无人直升机的抗干扰技术.

无人直升机应用于森林防火已经得到了国内外的广泛重视，为了提高其实用性，需大力发展其安全飞行控制技术.回馈递推控制作为一种有效的控制方法在无人直升飞行控制中已有较多的研究成果.文献[3]提出了一种小型无人直升机的姿态与高度自适应回馈递推控制方法；文献[4]对六自由度的无人直升机提出了一种自适应回馈递推控制方法.为了提高无人直升机在森林防火中的应用性能，必须提高其在森林环境干扰下的鲁棒飞行控制性能[5].滑模控制作为一种对系统干扰具有强鲁棒性能的控制方法，在无人直升机飞行控制中有着重要的应用前景，文献[6]对具有故障和风干扰的无人直升机提出了一种基于观测器的滑模控制方法.综上所述，欲高效实现对森林的巡逻和监控，必须大力发展抗扰性能良好的无人直升机飞行控制方法.

无人直升机为了在森林环境下安全飞行，必须与树木保持一定的距离.同时为了完成森林火灾监控，无人直升机也必须保持期望的飞行姿态.因而，为了保证无人直升机对森林火灾的安全监控必须考虑高度和姿态约束[7].文献[8]基于障碍李雅普诺夫(Lyapunov)函数方法对一类具有全状态约束的纯反馈系统提出一种了自适应控制方法.文献[9]利用性能转换函数方法为反馈线性化多输入多输出非线性系统设计了鲁棒自适应控制方法.文献[10-11]分别为3自由度直升机和6自由度无人直升机设计了保性能故障容错控制方法，但对森林环境下的无人直升机结合回馈递推控制和滑模控制方法设计满足高度和姿态约束的安全飞行控制方法还需要进一步研究.

本文针对森林环境下具有外部干扰的无人直升机的高度和姿态受限问题，研究了一种滑模安全飞行控制方法.采用误差性能转换函数方法处理对无人直升机的高度和姿态约束，并在变换后的系统基础上利用回馈递推方法和滑模控制方法设计了无人直升机的鲁棒飞行控制方法.

1 问题描述

如图1所示，应用无人直升机对火灾在内的森林异常与突发情况进行监控时，为保证无人直升机在复杂森林环境下具有很好的生存能力和安全性，须使其避开树木威胁且保持期望的飞行姿态.本研究重点考虑无人直升机高度姿态控制系统，因此无人直升机的高度和姿态控制问题转化为系统状态受约束的控制问题.

图1 无人直升机高度和姿态约束示意图Fig.1 Schematic diagram of altitude and attitude limitations for unmanned helicopter

为设计无人直升机安全飞行控制，先根据无人直升机的6自由度12状态非线性系统得到如下形式的高度姿态非线性模型[12]：

(1)

式中：z(t),v(t)∈R分别为无人直升机的垂直方向高度和垂直方向线速度；φ(t)，θ(t)，ψ(t)∈R分别为无人直升机的俯仰角、滚转角和偏航角；p(t)，q(t)，r(t)∈R分别为无人直升机对应方向上的姿态角速率；g为重力加速度；m为无人直升机质量；Tmr为无人直升机拉力；Jx、Jy和Jz为无人直升机的转动惯量；nx、ny和nz为无人直升机的3个方向上的力矩；dv(t)，dp(t)，dq(t)，dr(t)∈R为系统外部干扰.

为方便安全飞行控制器设计，定义

η=[zφθψ]T

ξ=[vpqr]T

u=[Tmrnxnynz]T

D=[dvdpdqdr]T

则无人直升机的高度姿态系统(1)可改写为

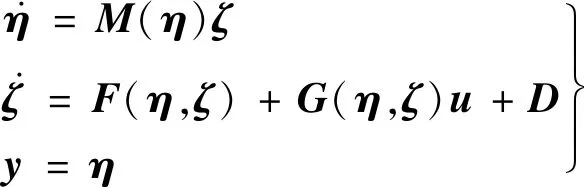
(2)

式中：

本文的控制目标为设计安全飞行控制律u，使得无人直升机高度姿态系统(1)在干扰作用下能够跟踪期望指令信号：

且跟踪误差满足指定的性能指标要求，其中zd、φd、θd和ψd分别为垂直方向高度、滚转角、俯仰角和偏航角期望输出.在控制器设计之前先做出如下假设：

假设1无人直升机高度姿态系统(1)的期望输出信号yd(t)及它的一阶和二阶导数都已知且是有界的.

假设2无人直升机高度姿态系统(1)的外部干扰dv(t)、dp(t)、dq(t)和dr(t)都是有界的.

假设3无人直升机高度姿态系统(1)的滚转角φ(t)和俯仰角θ(t)限定在有界区间，且取值满足-π/2<θ(t)<π/2和-π/2<φ(t)<π/2.

假设1假设无人直升机高度姿态系统式(1)的期望输出信号yd(t)及它的一阶和二阶导数有界.对于实际无人直升机，为完成给定任务，其期望跟踪信号是事先给定的，因而其为已知的.若期望跟踪信号不连续可导可能导致跟踪任务不可实现，则假设1是合理的.假设2要求无人直升机高度姿态系统(1)的外部干扰有界，若外部干扰无界则无人直升机不可控，则假设2是合理的.假设3为无人直升机防止出现奇异点的一个基本假设，即无人直升机在飞行过程中不会出现翻转.

2 安全飞行控制器设计

2.1 基于误差转换函数的输出受限处理

为设计无人直升机高度姿态系统的跟踪控制器，定义跟踪误差为

e=y(t)-yd(t)

(3)

为满足在森林环境下飞行的需要，对无人直升机的飞行高度和姿态需要给出严格的约束：

(4)

δi(t)=(δi0-δi∞)e-γit+δi∞

(5)

式中：δi(t)∈R，为递增函数；γi>0，为设计参数且决定了跟踪误差的收敛速度；δi0>0和δi∞>0为设计参数，决定了跟踪误差的收敛边界.

输出误差ei需要满足式(4)，对此类约束控制问题难以直接进行有效地处理.因此，为实现上述性能指标约束，利用文献[9]的结论，引入误差性能转换函数，将不等式约束问题转化为非约束问题：

(6)

式中：ρi为转换误差变量；Tc(·)为严格单调递增的光滑函数，且具有如下性质[9,11]：

因此，对跟踪误差ei的性能要求被转换为证明新的误差变量ρi的有界性.

考虑光滑递增函数Tc(·)的性质，选取如下形式的误差转换函数ρi保证跟踪误差ei的预设性能[11]：

(7)

根据文献[11]，式(7)中αc(ei(0)/δi(0))满足

令αci=αc(ei(0)/δi(0))，则误差转换函数(7)可改写为

(8)

对ρi进行求导可得

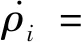
(9)

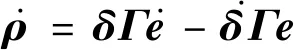
(10)

考虑e=y-yd和y=η，则可得

(11)

将转换误差动态式(11)与无人直升机高度姿态方程式(2)进行联立可得

(12)

2.2 基于回馈递推的无人直升机滑模安全飞行控制

本节在回馈递推控制方法的原理框架下，对转换后的系统(12)设计滑模控制器以保证原始系统(1)的跟踪性能，且满足给定的性能指标约束(4).

由式(11)可得

(13)

根据前述设计可知δΓM是可逆的，则设计虚拟控制律为

(14)

将转换误差动态(14)代入到式(13)可得

(15)

式中：正定矩阵K1为设计参数矩阵.

定义误差变量为

ω=ζ-ζd

(16)

则

(17)

设计滑模面：

s=c1ρ+c2z

(18)

其中：c1>0和c2>0为设计参数.考虑到式(13)和(17)则有

(19)

考虑到G(η,ζ)的非奇异性，设计控制律为

(20)

式中：正定矩阵K2和λ≥c2‖D‖为设计参数，且有 sgn(s)=[sgn(s1) sgn(s2) sgn(s3) sgn(s4)]T.

将式(20)代入式(19)可得

(21)

2.3 稳定性分析

根据上述无人直升机安全飞行控制分析和设计过程，可总结为如下定理：

定理1考虑在森林环境下受到干扰的无人直升机高度姿态系统式(1)，在满足假设1～3的条件下，如虚拟控制律和安全飞行控制器分别按式(14)和(20)设计，则所有的闭环系统信号都是收敛的，且系统输出误差满足给定的性能约束要求式(4).

证明：选取闭环系统的Lyapunov函数为

V=0.5ρTρ+0.5sTs

(22)

考虑式(15)和(21)，对式(22)求导得

(23)

-ρTK1ρ-sTK2s≤0

(24)

由式(24)可知，整个闭环系统信号是收敛的，定理1证明完毕.

众所周知，滑模控制由于符号函数的引入，会导致控制律不断切换，从而导致颤振.为了消除符号函数给飞行控制带来的不利影响，根据文献[12]，将饱和函数引入替代符号函数，以提高闭环控制系统性能.替代后的控制器为如下形式：

(25)

式中：sat(·)为饱和函数.同时，实际参数K1和K2选取越大，闭环控制性能越好.

3 仿真分析

为了对所研究的无人直升机安全飞行控制算法的有效性进行验证，本节进行数值仿真验证.仿真中无人直升机的参数选取为m=800 kg，g=9.8 m/s2，Jx=358.4 kg·m2，Jy=777.9 kg·m2和Jz=601.4 kg·m2 [13].无人直升机高度姿态系统的初始高度和初始姿态角分别设定为z(0)=-150 m，φ(0)=0.06 rad，θ(0)=0 rad，ψ(0)=0.05 rad.无人直升高度姿态系统的期望的参考轨迹选为

zd=-150-12[1-exp(-5t)] m

φd=0.15sin(0.5t) rad

θd=0.1sin(0.3t) rad

ψd=0.3sin(0.4t) rad

无人直升高度姿态系统的外部干扰选为

dv=2.5sin(0.3t)

dp=1.5sin(0.3t)

dq=0.8sin(0.4t)

dr=1.3sin(0.6t)

性能指标函数δi选取为

δ1=2exp(-t)+0.05

δi=0.4exp(-t)+0.02,i=2,3,4

控制器的相关设计参数选为

虚拟控制律和安全飞行控制器分别按式(14)和(20)设计，则在所设计的控制器作用下无人直升高度姿态系统对期望跟踪信号的跟踪误差曲线如图2～5所示.由仿真结果图可得知，在所设计的安全飞行控制器作用下，受到扰动作用的无人直升高度姿态系统对期望信号的跟踪误差都位于事先给定的约束界之内，因而所设计的控制器是有效的，能满足森林环境下对无人直升机的使用要求.

图2 高度跟踪误差曲线Fig.2 Error of altitude tracking

图3 俯仰角跟踪误差曲线Fig.3 Error of pitching angle tracking

图4 滚转角跟踪误差曲线Fig.4 Error of roll angle tracking

图5 偏航角跟踪误差曲线Fig.5 Error of yaw angle tracking

4 结语

为了提高森林环境下无人直升机的飞行控制安全性，在飞行跟踪控制器设计时考虑高度和姿态约束.利用误差性能转换函数方法对系统约束进行处理，结合回馈递推方法和滑模方法设计了无人直升机的鲁棒飞行控制方法，其中无人直升机所受外部干扰影响由滑模控制处理.采用Lyapunov方法证明了整个闭环系统的稳定性.通过仿真可以看出，本文所提出的方法能实现对跟踪信号的有效跟踪，且跟踪误差信号能保持在给定的误差界之内.